水下捕捞机器人水动力学性能分析

刘芳华，李 鑫

(江苏科技大学机械工程学院，江苏 镇江 212003)

0 引言

海参捕捞机器人的工作环境是在5～15 m之间的近海海底，由于近海风浪和潮涌对海参捕捞机器人的运动具有很大影响，因此为实现海参捕捞机器人在水下更稳定地抓取海参，需要对海参捕捞机器人工作姿态下的水动力学进行分析，探究机器人在水平直航、水平斜航和垂直斜航时所受到的水流的阻力和阻力矩。但要准确地描述捕捞机器人在水下不同姿态下的水阻力和水阻力矩，需要获得精确的水动力学参数，从而建立可靠的水动力学模型。一般的获取方法有：理论或经验公式计算、拖曳水池实验和计算流体力学(CFD)数值模拟[1]。

随着计算机技术的飞速发展，基于计算流体力学的水动力模拟方法也得到越来越多的重视。相比于传统的方法，CFD数值模拟具有计算成本低、无需考虑缩尺比和无加工误差等优点，对水动力分析的影响较小，能获得更加接近实际的水动力学参数等优势，故该方法被应用于许多水下机器人的水下仿真分析[1-8]。但到目前为止，国内外还没有专门针对海参捕捞机器人的水动力学研究，因此，本文利用CFD数值模拟法对海参捕捞机器人进行水动力学仿真分析，并通过求得的水动力系数拟合出水阻力-速度、水阻力矩-速度和水阻力矩-角度的关系，从而得出最大水阻力和水阻力矩，为外形优化和推进器选型提供参考。

1 水动力计算模型的建立

1.1 海参捕捞机器人总体结构

海参捕捞机器人的结构如图1所示。海参捕捞机器人外形尺寸为1 000 mm×800 mm×625 mm，其总体采用框架式的结构形式，总体结构布局为：框架由铝合金板焊接而成；捕捞机械臂安装在框架前上部，其上固定有水下摄像头；浮体覆盖安装在框架上部，两边开有对称的推进器导流槽；在框架内部对称安装有控制舱、垂向推进模块、纵向推进模块和横向推进模块；水下探照灯和储物箱悬挂安装在框架下方。

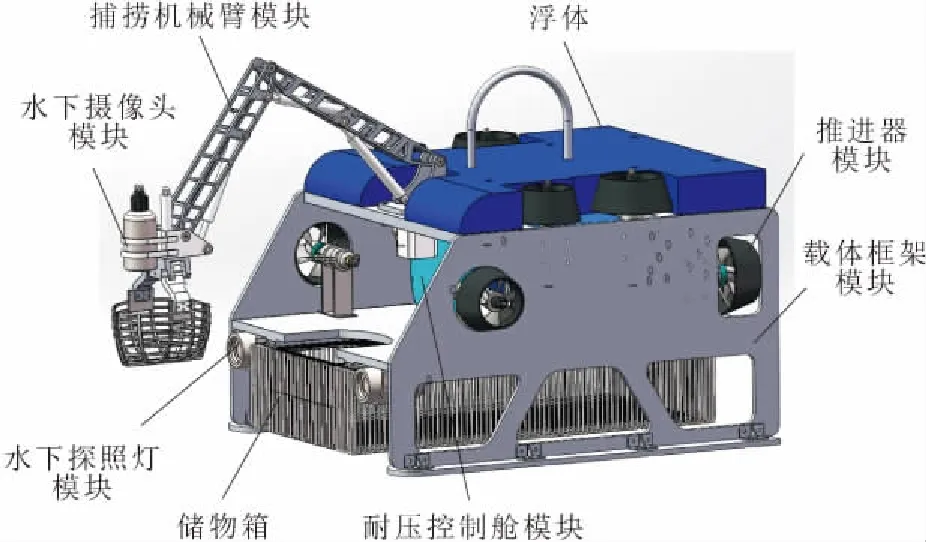
图1 海参捕捞机器人结构

1.2 湍流数学模型的建立

所有和流体流动有关的现象都满足质量守恒和动量守恒定律[4]，而对海参捕捞机器人的水动力学分析不涉及能量的交换问题，因此直接用质量守恒和动量守恒方程即可作为控制方程进行水动力学计算。三维瞬态不可压缩流体的质量守恒方程[2]为

(1)

t为时间；ρ为液体密度；uj为沿着x坐标轴的速度分量；Sm为单位时间内液体质量的增量。

惯性坐标系下的动量守恒方程[2](Navier-Stokes方程)为

(2)

p为单位流体上的静压力；gi为沿着x坐标轴的重力分量；Fi为沿着x坐标轴的外力分量；τij为粘性应力。

由于海参捕捞机器人的工作环境是在5～15 m之间的近海海底，会有明显的风浪和潮涌，因此需要选择适当的湍流模型。目前，被广泛采用的湍流模型是对N-S方程进行雷诺平均和滤波处理后的方程，即雷诺时均Navier-Stokes(RANS)方程：

(3)

(4)

k为湍流动能;μt为湍流粘度。引入一个变量ε并利用一个函数关系式可确定它们之间的关系：

(5)

Cμ为经验常数；ε为湍流耗散率。

由式(5)可知，湍流粘度可采用k和ε来表示，即标准k-ε方程模型。其变量方程为

(6)

但是，标准的k-ε模型在用于湍流漩涡或高速张紧流体时会出现一定的失真，这将导致计算的精度有所下降，因此本文应用改进型的标准k-ε模型，即RNGk-ε模型。

RNGk-ε模型变量方程为

(7)

μeff为有效粘度，μeff=μ+μt；Sk和Sε为源项；Gk为平均速度梯度引起的湍流动能。

1.3 近壁区域的处理

需要注意的是，RNGk-ε模型只适用于高雷诺数的湍流情况，而在真实的近海捕捞作业的环境中，捕捞机器人的外壁会对湍流流动产生明显的干扰，其中平均速度场受壁面无滑移因素的影响较大。近壁区域的粘性阻尼使得流体介质的流动被限制，这造成机器人外壁附近的速度梯度变化巨大而产生了湍流动能，进而导致湍流流动迅速扩张。基于这些因素，近壁区域不能完全使用RNGk-ε模型来进行计算，必须进行特殊的处理。

根据以前的实验可知，近壁区域由介质流动情况的不同可划分为3层区域[9]，最靠近壁面的一层为粘性底层，该层是一个紧贴外壁面的极薄层，这一层中介质主要以层流形式存在；最外层为对数律层，该层是产生湍流的核心区域；在粘性底层和对数律层中间是过渡层，其中介质流动极为复杂，难以用适合的模型进行描述。要对这3层区域进行详细描述，主要有2种方法：第1种是近壁建模法，它需要对湍流模型进行修改，以此来求解粘性底层和过渡层；第2种是标准壁面函数法，这种方法不对粘性底层和过渡层进行求解，而是利用半经验公式(标准壁面函数)将机器人外壁与对数律层湍流区域直接连接，也即将求解的第1个节点直接布置在对数律层里，其内不再配置节点。近壁建模法与标准壁面函数法的对比如图2所示。

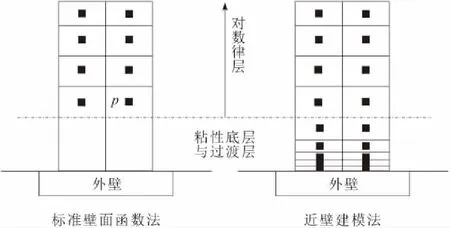
图2 近壁建模法与标准壁面函数法的对比

标准壁面函数公式为

(8)

其中

(9)

(10)

p为对数律层中的一个内节点；k为冯卡门系数；E为经验常数,E=9.81；Up为p点的平均速度；kp为p点的湍流动能；yp为p点到外避面的距离；τω为壁面切应力；μ为流体的动粘度。

近壁区域中的湍流动能k和其耗散率ε需要单独计算,其变量方程为

(11)

在RNGk-ε模型中应用上式进行近壁区域计算，可以使仿真结果更加准确。

1.4 计算模型网格划分及计算域的设置

由于海参捕捞机器人采用框架式结构，形状结构较为复杂，若将其直接进行网格划分，工作量较大，时间较长，且对电脑配置有一定要求。因此，在保证水动力分析结果的前提下，可将一些阻力较小的结构进行模型简化[10]，简化后的模型如图3所示。

计算域流场(domain2)采用长方体形状，如图4所示，长方体的前端为流场入口(inlet)，后端为流场出口(outlet)[11]。假设海参捕捞机器人的前后长度为L=1 000 mm，则计算域流场的总长为13L=13 000 mm，其中从入口至捕捞机器人正面的长度为4L=4 000 mm，捕捞机器人后面至计算域出口的长度为8L=8 000 mm，而计算域流场的左右面和上下面与捕捞机器人的壁面距离应该至少为2倍[12]的海参捕捞机器人长度，即为4L=4 000 mm。将简化后的海参捕捞机器人模型先放入计算域domain2中，使其正面正对计算域流场入口，再在模型周围创建一个长宽高均为1.3L的计算域(domain1)，该计算域是为了方便近模型区域的网格划分。

图3 海参捕捞机器人的简化模型

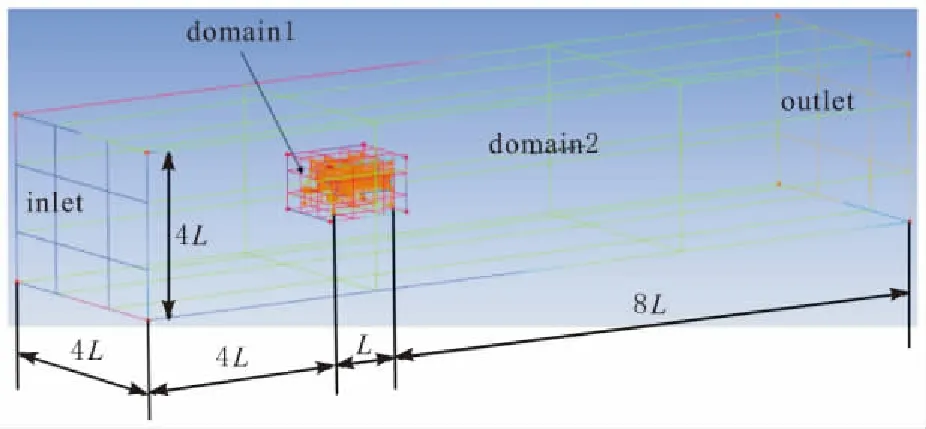
图4 计算域流场

网格划分是水动力仿真分析的关键。网格过少会导致计算精度过低，影响最终仿真结果的准确性；网格过多，则会使计算时间过长，增加计算机的负担。因此，在确保仿真准确性的同时节省计算资源，采用分区域混合网格划分的方法，即将捕捞机器人和靠近捕捞机器人周围的计算域domain1采用非结构化网格并进行加密处理，而domain2中除了domain1的计算域外其余部分采用结构化的网格划分。划分网格后的整体计算域如图5所示。图6是domain1中的非结构化网格。

综上，本研究将以同一偶像团体粉丝群体内部关系作为研究的出发点和落脚点，将运用科塞的社会冲突理论，研究同一偶像组合的粉丝群体内部分离出来的不同的粉丝属性之间冲突关系的形成，探究不同粉丝属性下冲突关系的正功能和负功能，以及如何维系关于冲突关系的建构，分析其建构背后的意义。

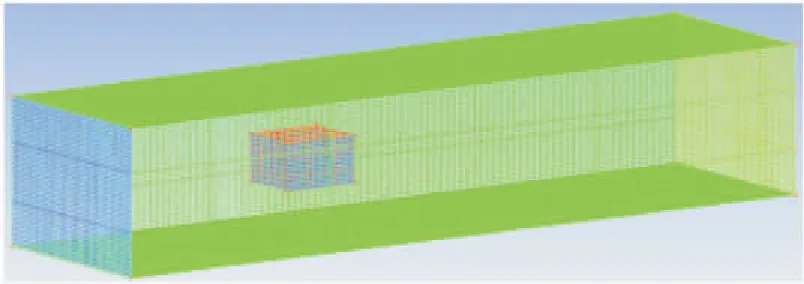
图5 整体计算域网格

图6 domain1非结构化网格

2 水动力性能分析

2.1 水动力分析原理及参数设置

海参捕捞机器人在水下作业时主要会处在3种工作状态，即水平直航(向前搜寻)、水平斜航(换向)和垂直斜航(越障)。对于水阻力的分析，即海参捕捞机器人以不同速度在这3种状态下所受到的水阻力，本文在Fluent中让水流以不同速度冲击固定的海参捕捞机器人来仿真，可达到相同效果；对于水阻力矩的分析，可将海参捕捞机器人近似看作一个正方体，则它所受到的水阻力矩即为不同速度的水流产生的水阻力绕模型中心旋转时产生的力矩。由于Fluent中不可直接计算导出水阻力和水阻力矩，因此需要通过如下2个经验公式转换：

(12)

(13)

F为水阻力；T为水阻力矩；ρ为流体密度；A为迎流面积；L为阻力臂；Cd为水阻力系数；Cm为水阻力矩系数。

水动力性能分析前，在Fluent中设置流场入口为速度入口(velocity-inlet)边界条件，流场出口为自由出口(outflow)边界条件，计算域边界和计算模型都为固体壁面(wall)边界条件。湍流模型采用RNGk-ε模型，并结合基于压力变量的SIMPLE耦合求解器求解压力速度方程组。在空间离散参数求解设置中，利用Green-Gauss Cell Based法求解梯度方程，压力采用Standard方式离散，动量、湍流动能和湍流耗散率均采用First Order Upwind格式进行离散。

2.2 水平直航水动力性能分析

由于海参捕捞机器人在水下捕捞海产品时不需要太快的移动速度，因此在速度入口边界条件中分别设置流场速度为0.2 m/s、0.4 m/s、0.6 m/s和0.8 m/s。利用对捕捞机器人4种流速下的水下阻力特性进行计算，所得结果如表1所示。

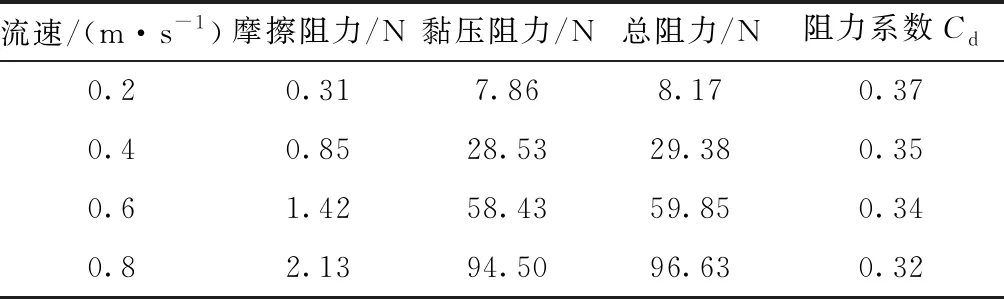
表1 海参捕捞机器人直航阻力特性

由表1可以看出，流速和摩擦阻力、黏压阻力均成正相关，同时由于海参捕捞机器人特殊的框架结构形式，其黏压阻力占总阻力的比重很大。直航时总阻力的变化曲线如图7所示，其垂向力变化曲线如图8所示，俯仰力矩变化曲线如图9所示。

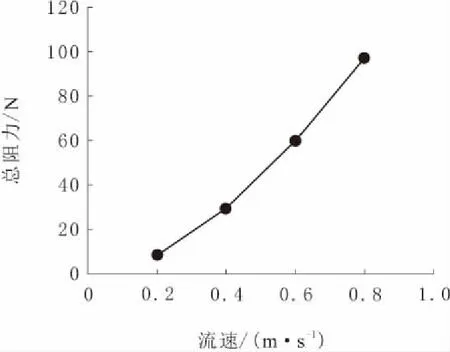
图7 直航总阻力变化曲线

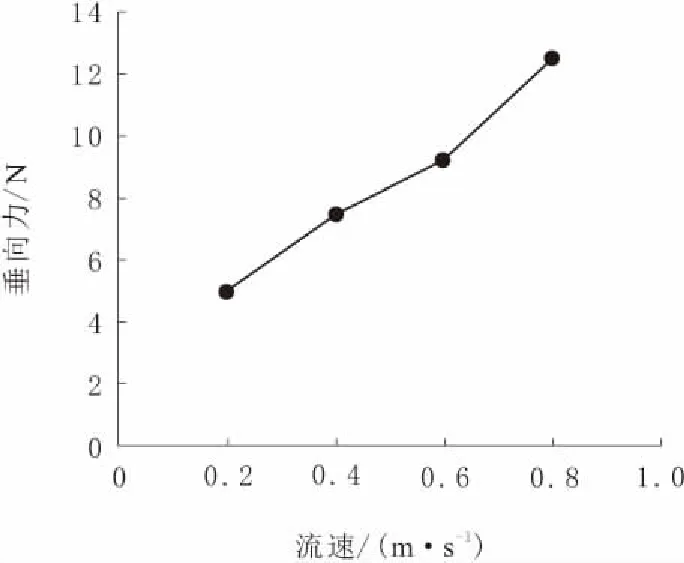
图8 直航垂向力变化曲线

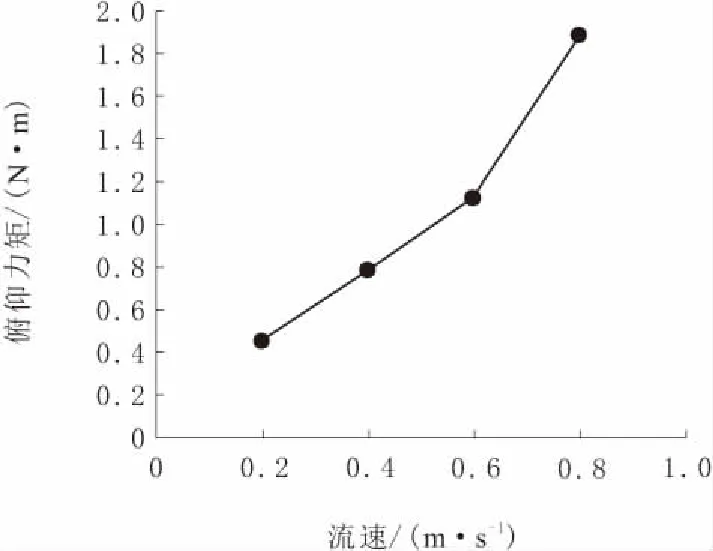
图9 直航俯仰力矩变化曲线

由图7～图9可知，当直航流场流速达到最大时，捕捞机器人所受最大阻力为99.63 N；由于其本身框架结构的复杂性和结构的不对称性，导致其在水下直航时受到整体垂直向下的作用力，并随着流速的增加而增大；同时，由于直航不涉及仰角的变化，捕捞机器人直航时产生的俯仰力矩较小，对其航行时的影响可忽略不计。

2.3 水平斜航水动力性能分析

海参捕捞机器人在水下作业时会经常遇到不停转向进行搜捕的情况，因此需要对捕捞机器人水平斜航状态下的水动力进行分析。分别设置流场速度0.2 m/s、0.4 m/s、0.6 m/s和0.8 m/s，漂角分别为0°、2°、4°、6°、8°和10°，利用Fluent软件在6种漂角下对捕捞机器人的4种流速状态的水下阻力特性进行计算。图10～图12分别为海参捕捞机器人水平斜航时受到的横向力、纵向力和垂向力随漂角变化的曲线。

图10 水平斜航横向力变化曲线

图11 水平斜航纵向力变化曲线

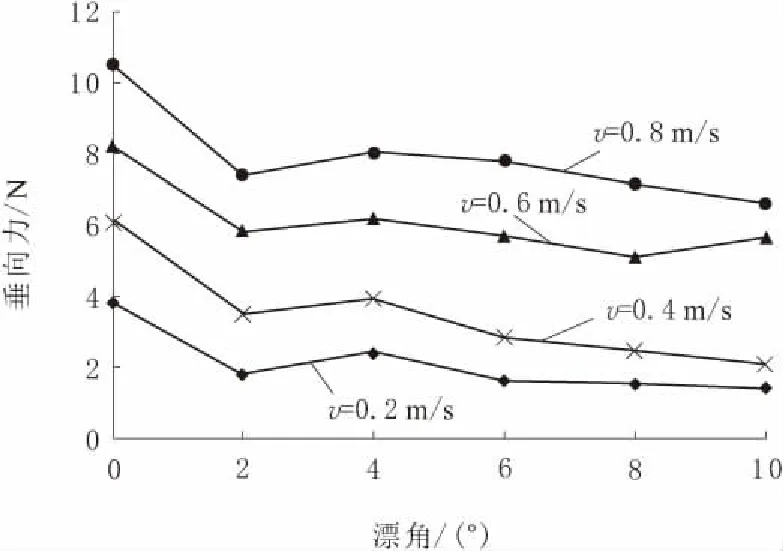
图12 水平斜航垂向力变化曲线

由图10～图12可知：当海参捕捞机器人在水下以一定漂角斜航时，其横向力随着流场流速的增加而增大，在同一流速下横向力的大小随着漂角的变大而明显增大，若以最大漂角和最高流速斜航时，捕捞机器人会受到约22.33 N的横向力，因此当海参捕捞机器人在一定区域内连续转向搜捕时，需要考虑转向驱动力以及横向海流对捕捞机器人捕捞作业时产生的影响；捕捞机器人纵向力随着流速的增加而显著增大，最大可达到99.80 N，但是同一航速下的纵向力变化不大，这表明在捕捞机器人作业时，较小的横向海流对其纵向阻力基本没有影响，这是由于捕捞机器人特殊的开架式结构，各种零件分散的布置在载体框架的各个部位，导致其漂角变化时迎流面积并没有发生太大的变化；捕捞机器人所受垂向力方向垂直于前进方向向下，并随着流场流速的变大而变大，但在同一航速下垂向力随着漂角的增加而减小，从数值大小来看垂向力对捕捞机器人水平斜航时的影响不大。

2.4 垂直斜航水动力性能分析

海参捕捞机器人在水下作业时会遇到以一定角度下潜或者爬升的工况，因此需要对其垂直斜航的水动力进行分析。由于海参捕捞机器人上下结构并不对称，因此垂直斜航水动力分析需要对正负攻角分别进行分析。

a.正攻角垂直斜航水动力分析。设置流场速度分别为0.2 m/s、0.4 m/s、0.6 m/s和0.8 m/s，攻角分别为0°、4°、8°、12°和16°，重新设置长方体流场域domain2的下侧和前端为速度入口(velocity-inlet)边界条件，上侧和后端为速度出口(outflow)边界条件，利用Fluent软件在5种攻角下对捕捞机器人4种流速状态的水下阻力特性进行计算。图13～图15分别为海参捕捞机器人正攻角垂直斜航时受到的垂向力、纵向力和俯仰力矩随攻角变化的曲线。

b.负攻角垂直斜航水动力分析。设置流场速度分别为0.2 m/s、0.4 m/s、0.6 m/s和0.8 m/s，攻角分别为-16°、-12°、-8°、-4°和0°，重新设置长方体流场域domain2的上侧和前端为速度入口(velocity-inlet)边界条件，下侧和后端为速度出口(outflow)边界条件，利用Fluent软件在5种攻角下对捕捞机器人4种流速状态的水下阻力特性进行计算。图16～图18分别为海参捕捞机器人负攻角垂直斜航时受到的垂向力、纵向力和俯仰力矩随攻角变化的曲线。

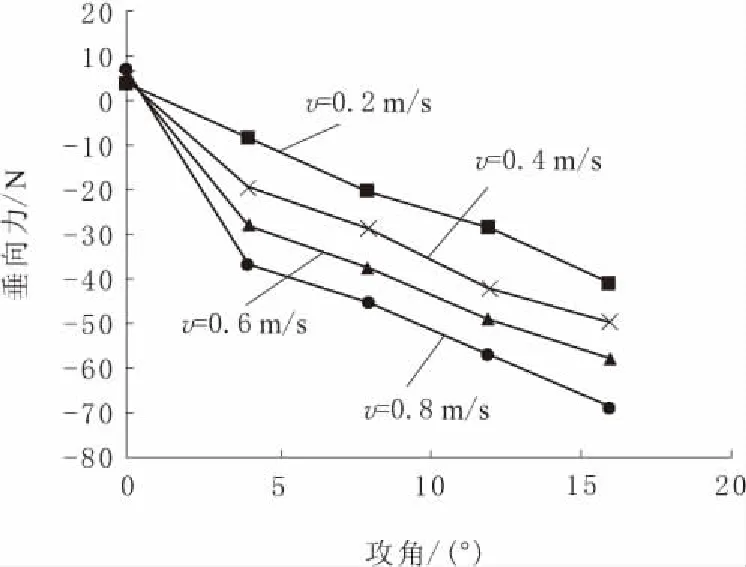
图13 正攻角垂向力变化曲线

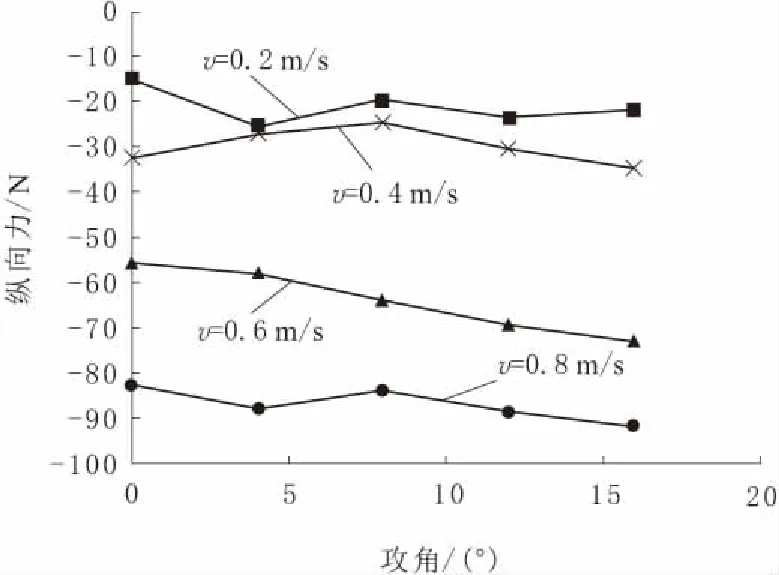
图14 正攻角纵向力变化曲线

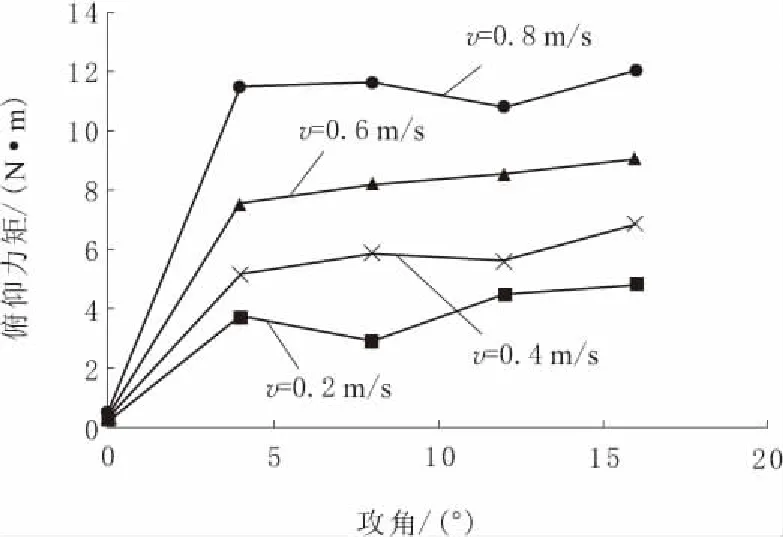
图15 正攻角俯仰力矩变化曲线

由图13～图18可知：虽然海参捕捞机器人上下结构不对称，需要对正负攻角分开分析，但是得到的仿真分析结果相似；当捕捞机器人以正攻角或负攻角运动时，其所受垂向力均随着流场流速的增加而增大，在同一流速下垂向力随着攻角绝对值的增大而显著增加，2种运动状态的最大垂向力均能突破70.00 N，这是由于当攻角绝对值越大时，浮体表面以及底盘下表面的迎流面积就越大，从而导致阻力增加；纵向力随流速的增加而产生明显变化，其绝对值最大可达92.44 N，但在同一流速下攻角对纵向力的影响较小；俯仰力矩随流速的变大而增加，同一流速下随攻角的增加而显著增大。

图16 负攻角垂向力变化曲线

图17 负攻角纵向力变化曲线

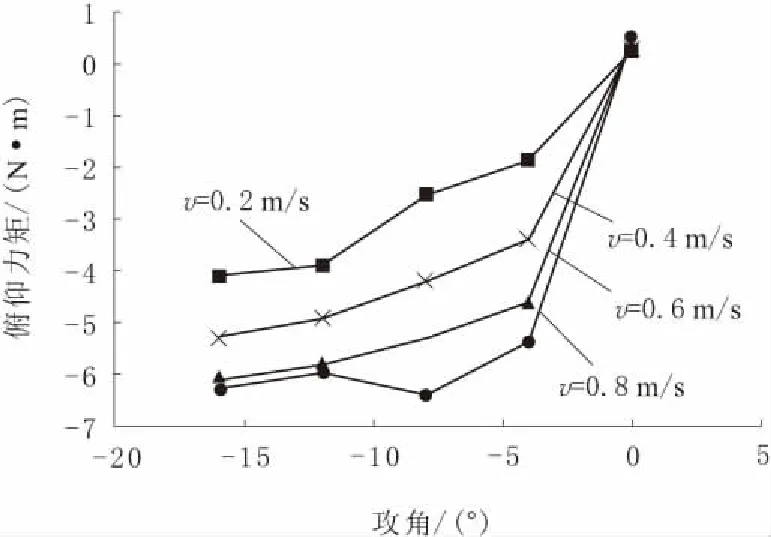
图18 负攻角俯仰力矩变化曲线

3 结束语

通过分析并模拟了捕捞机器人在水平直航、水平斜航和垂直斜航3种状态下的受阻力情况，拟合出3种状态下水阻力和俯仰力矩的变化曲线，可得出以下结论：

a.由于海参捕捞机器人采用了开放式框架结构，在结构上具有复杂性和不规则性，因此必须结合实际应用考虑以上3种状态。

b.通过水动力分析，可得3种状态下捕捞机器人的受力情况。当最大水流速度为0.8 m/s时，水下捕捞机器人水平直航所受的最大阻力为96.63 N；水平斜航时受到横向力和纵向力影响较大，所受最大横向力为22.33 N，最大纵向力为99.80 N；纵向力和垂向力对垂直斜航有较为明显的作用，所受最大纵向力为92.44 N，最大垂向力为71.71 N。由此可以推导出：尾部2个推进器需要提供100.00 N的推力，即每个提供50.00 N；左右2个推进器需要提供30.00 N的推力，即每个提供15.00 N；中间后2个推进器需要提供80.00 N的推力，即每个提供40.00 N的推力；而中间前2个需要控制捕捞机器人整体的浮沉，由于设计时使捕捞机器人在水下处于悬浮状态，只需很小的力便可使其浮沉，因此中间前2个推进器提供30.00 N的推力足矣。

以上分析结果可为海参捕捞机器人的结构优化和推进系统的选型提供参考依据。