模糊交叉耦合控制在跟踪雷达伺服系统中的应用

程仕祥,王劲宣,王志勇,费志洋,史乃青

(中国电子科技集团公司第三十八研究所，安徽 合肥 230088)

0 引言

在精密跟踪雷达中，伺服系统的跟踪误差在测角误差中占有较大比重，伺服系统中的跟踪误差包括方位轴跟踪误差、俯仰轴跟踪误差，以及两轴综合而成的系统跟踪误差。对二维跟踪雷达而言，伺服系统中各类误差的影响最终都可通过系统跟踪误差的大小体现出来，而系统跟踪误差又容易受到各类噪声和扰动、机械惯性，以及两轴响应速度不匹配等因素的影响[1]。

目前，绝大多数的二维跟踪雷达伺服系统采用的都是非耦合控制。也即各单轴独立控制。虽然此法在一定程度上能减小系统跟踪误差，但却将整个伺服系统割裂开来，没有考虑到各轴之间存在的耦合关系，这就导致不能准确地反映出雷达伺服系统整体的运行情况。交叉耦合控制理论是由Koren[2]等人于1985年首次提出，在一定程度上提高了多轴联动系统的跟踪精度，改善了控制性能。随后多年，许多学者将交叉耦合控制及其改进理论应用于各行各业的多轴联动控制系统中，并相继取得一定的成果[3]。

本文在二维跟踪雷达伺服系统中，设计一种变增益交叉耦合控制与模糊控制相结合的控制算法，并在MATLAB/Simulink环境下建立仿真模型。仿真对比和实际工程验证表明，该控制算法可有效提高方位轴和俯仰轴之间的协调性，进而显著减小系统跟踪误差，提高跟踪精度。

1 雷达伺服系统跟踪误差数学模型

二维跟踪雷达伺服系统通常由以下几部分组成：雷达底座和支架、方位轴伺服电机及减速机、俯仰轴伺服电机及减速机、伺服驱动器、传动机构以及雷达天线。雷达天线的转动角度由方位轴电机和俯仰轴电机联动控制，实现对目标的搜索和跟踪。

雷达天线在追踪和监控目标时，其在空间运行的轨迹可以用三维立体球面来表示[4]。如图1所示，以雷达天线的中心为坐标原点O，按右手螺旋定则建立空间笛卡尔直角坐标系XYZ，雷达天线空间运动轨迹上的任一目标点A与Y轴的夹角为俯仰角α，对应俯仰轴的输入角度；A点在XOZ面上的投影点A″与Z轴的夹角为方位角β，对应方位轴的输入角度；点A到圆心O的距离为R，则可以用三维坐标表示出雷达天线运动轨迹上的任一目标点，如点A表示为(Rsinαsinβ，Rcosα，Rsinαcosβ)。

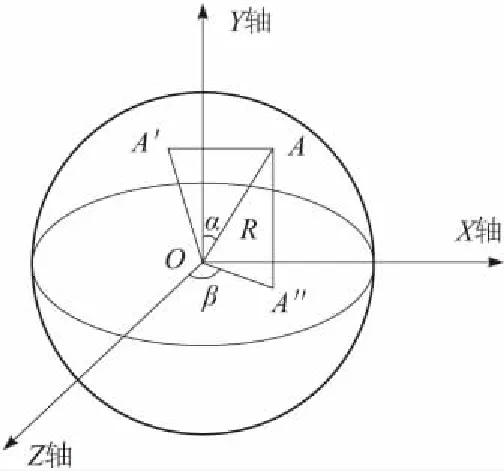
图1 雷达天线空间运行轨迹

由于只需对方位轴和俯仰轴进行控制，所以将雷达天线空间运动轨迹投影到ZOY平面上，得到投影曲线C以及点A对应的投影点A′(Rsinαcosβ，Rcosα)，且点A′在投影曲线C上。根据被跟踪目标的轨迹，投影曲线C可分为直线轨迹和任意曲线轨迹，具体每种情况下系统的跟踪误差数学模型分别如图2和图3所示。

(1)

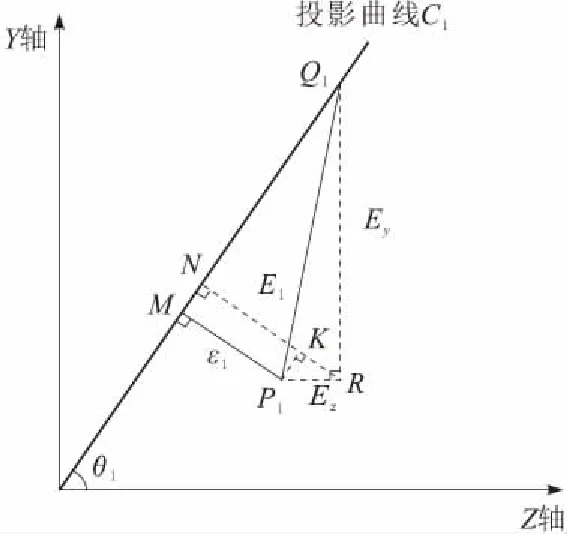
图2 直线轨迹的系统跟踪误差示意

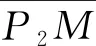
Ey·cosθ2-Ez·sinθ2

(2)

图1中，A′点在Y轴和Z轴上的位置分别为：y=Rcosα，z=Rsinαcosβ。因此A′点所在投影曲线C可用如下关系表达：

y=Rcosα，z=Rsinαcosβ

(3)

不管投影曲线C为何种类型的轨迹，都有

(4)

则

(5)

因此，无论投影曲线C为何种类型的轨迹，系统的跟踪误差都可以用下式表达：

(6)

2 雷达伺服系统中的变增益模糊交叉耦合控制

交叉耦合控制是针对整个系统进行统一的控制，其核心思想是在各单轴独立控制的基础上，设计一个模块对各单轴的角度跟踪误差进行综合运算，然后将所得结果分别按对应的增益系数分解给各轴，对各轴进行针对性补偿以减小跟踪误差。如图4，在本文所研究的跟踪雷达伺服系统中，俯仰和方位的输入角度分别为α和β，实际输出为α*和β*，将俯仰轴的跟踪误差eα和方位轴的跟踪误差eβ与交叉耦合增益系数C1、C2相乘，并代入上述系统跟踪误差数学模型，得到系统的跟踪误差ε，随后经模糊PID控制器的调节，得到调节后的系统跟踪误差ε*，再通过C1、C2重新分配给俯仰轴和方位轴。这样就在单轴的跟踪中包含了整个系统的状态信息，从而可有效改善系统的跟踪精度。

图4 基于变增益模糊交叉耦合控制的雷达伺服系统原理

与传统的交叉耦合控制相比，一方面，图4中的交叉耦合增益系数C1、C2并非固定参数，而是输入角度α和β的函数，具体如式(7)和式(8)所示，它们能根据系统输入的改变进行相应的调整，使交叉耦合控制更加有利于雷达的实际应用[5]。

(7)

(8)

另一方面，在交叉耦合控制算法中，以模糊PID控制器取代传统PID控制器，以增强系统灵活跟踪的能力，在满足快速性要求的同时，又能极大地改善耦合控制的自适应性。

在进行模糊PID控制器的设计时，选取计算所得的系统跟踪误差ε及其变化率εc，作为模糊控制器的输入信号，模糊控制器的输出为ΔKP、ΔKI、ΔKD。输入变量和输出变量被标准化到[-6,6]，即系统跟踪误差ε和变化率εc从基本论域分别乘以量化因子Ke和Kec，变换至对应的模糊论域E[-6,6]和EC[-6,6]，在完成模糊化处理后，将获得的模糊量作为模糊推理系统的输入；利用依据专家经验建立的模糊规则进行模糊推理，获得模糊量；再通过面积中心法解模糊，将解得的模糊量转换为精确的输出量；最后再将输出量对应乘以比例因子KPG、KIG、KDG，得到比例系数、积分系数、微分系数的调节量ΔKP、ΔKI、ΔKD，并与PID控制器中3个参数KPccc、KIccc、KDccc对应相加，以实现对PID控制器中参数的实时自适应调整[6]。

本文的模糊语言变量的设计如下：输入变量模糊论域E、EC，输出变量ΔKP、ΔKI、ΔKD的语言值均设置为5个，即负大(NB)、负小(NS)、零(ZO)、正小(PS)和正大(PB)。输入、输出隶属度函数均以高斯型隶属函数的形式来表示，结合Mamdani模糊推理，建立Mamdani型模糊系统。

3 仿真结果与分析

3.1 仿真模型

为了检验本文所设计的变增益模糊交叉耦合控制算法在二维跟踪雷达伺服系统中的控制效果，在MATLAB/Simulink环境下搭建仿真模型，如图5所示。

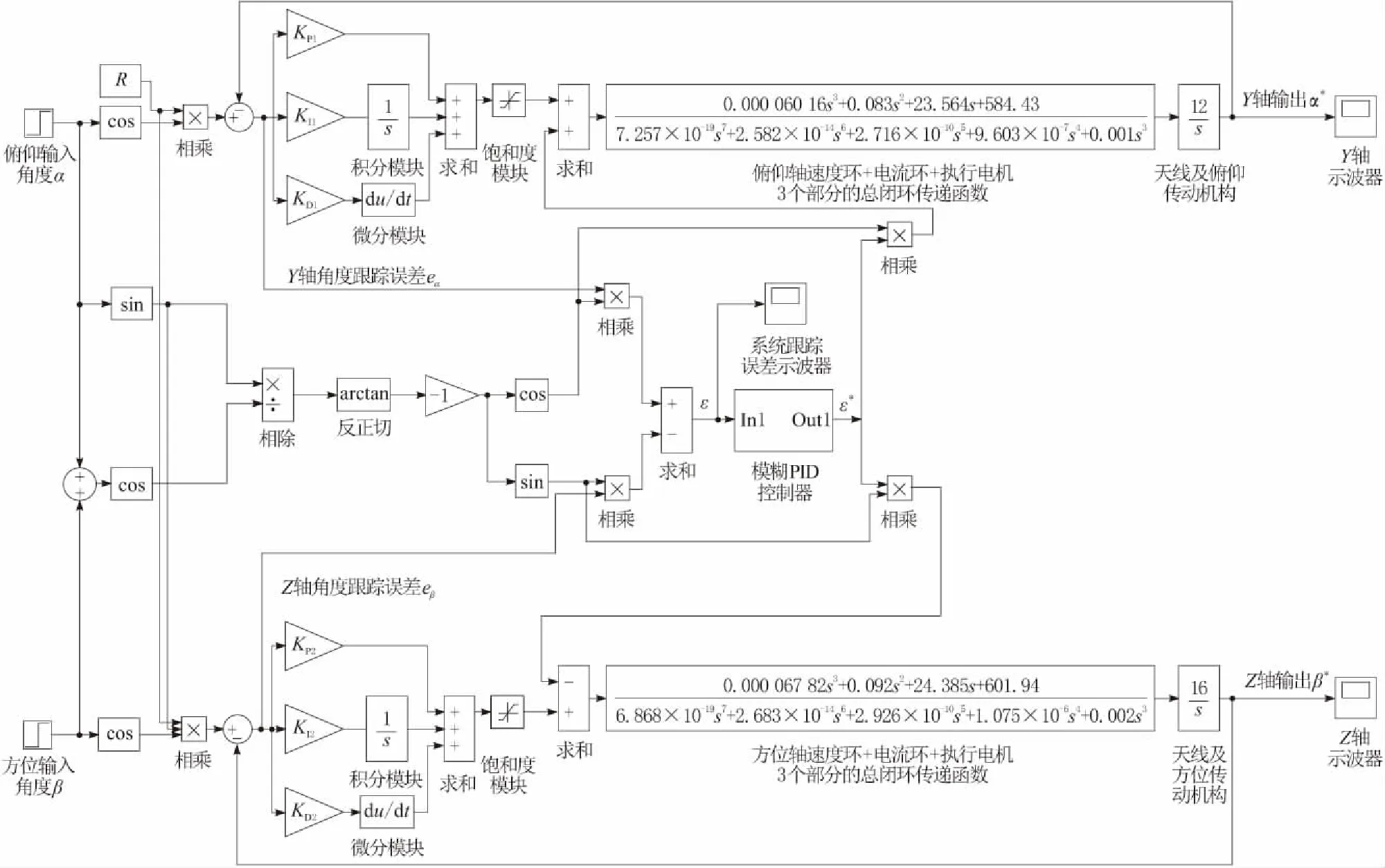
图5 基于变增益模糊交叉耦合控制的二维跟踪雷达伺服系统仿真模型

图5中，俯仰轴和方位轴均采用永磁同步伺服电机，且二者的位置环都采用PID控制。各部分的参数如下：俯仰轴位置环，KP1= 4.75，KI1= 1.8，KD1= 0.25；方位轴位置环，KP2= 5，KI2= 1.5，KD2= 0.2；交叉耦合控制模块中模糊PID控制器里相关的PID参数为KPccc= 4.75，KIccc= 1.8，KDccc= 0.25；其余各部分均以传递函数的形式表示。

3.2 仿真结果与分析

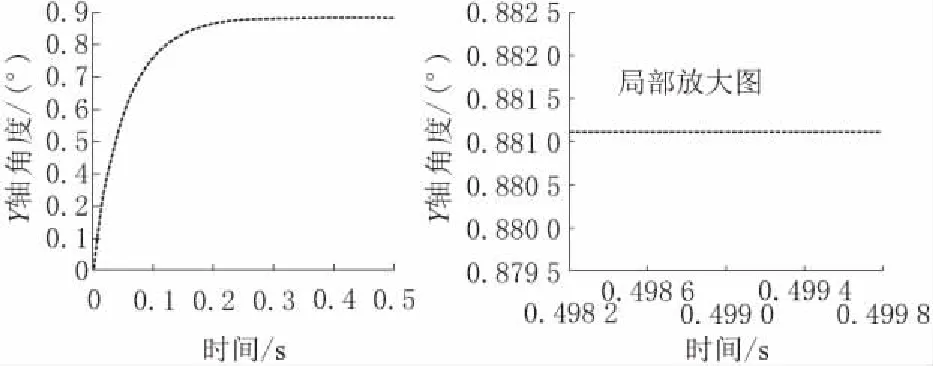
图6 无耦合时Y轴响应曲线

图7 无耦合时Z轴响应曲线

图8 变增益模糊交叉耦合时Y轴响应曲线

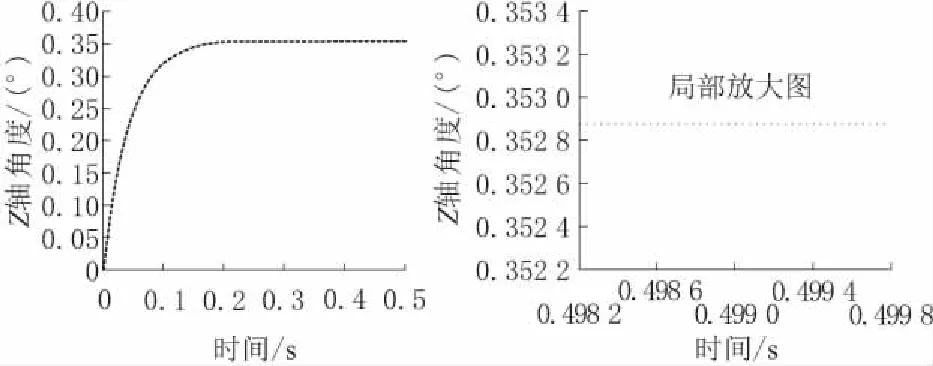
图9 变增益模糊交叉耦合时Z轴响应曲线

对比图6和图8，可以得出Y轴在无耦合控制下的稳态误差为-0.015 1°，而在变增益模糊交叉耦合控制下的稳态误差为-0.012 7°；对比图7和图9，可知Z轴在无耦合控制下的稳态误差为-0.003 8°，而在变增益模糊交叉耦合控制下的稳态误差为0.000 7°。又可由公式(6)计算得到无耦合控制下系统的稳态跟踪误差为-0.010 5°，而在变增益模糊交叉耦合控制下系统的稳态跟踪误差为-0.005 2°。可以看出，变增益模糊交叉耦合控制算法可以有效抑制二维跟踪雷达伺服系统的跟踪误差，显著提高伺服系统的跟踪精度。

为对上述仿真结论进行更多的验证，另选取2组不同的输入条件进行对比仿真，结果如表1所示。

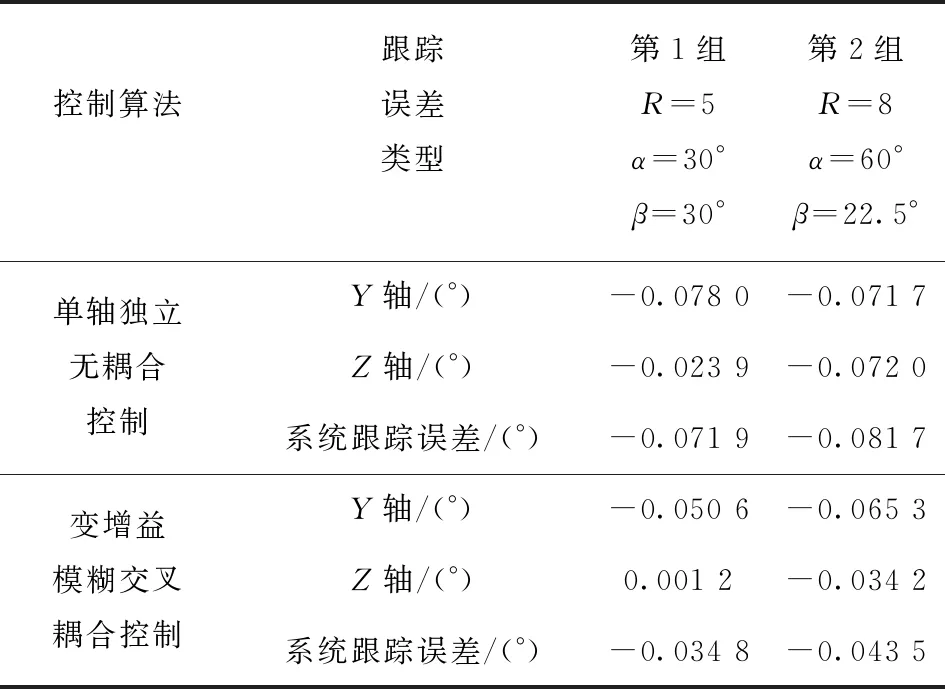
表1 2种控制算法下的跟踪效果

由表1可知，采用变增益模糊交叉耦合控制算法时，各单轴及整个系统的跟踪误差都有不同程度的减小，表明系统的跟踪性能得到有效改善，这和前面的仿真结论相一致。

4 工程验证

为验证所设计控制算法的工程可实现性，在某型跟踪雷达上进行了工程试验验证。其中，天线车单元主要包括天线阵面、方位-俯仰型天线座、汇流环和伺服控制分系统等部分，主要设备组成如图10所示。

图10 某型跟踪雷达主要设备组成

在PCC可编程逻辑控制器中，将本文所设计的变增益模糊交叉耦合控制算法编写到运动控制程序。试验时，设定伺服系统方位轴和俯仰轴都发出相同的阶跃输入指令(30°)，得到单轴独立无耦合控制时的系统跟踪误差为0.093°，而在变增益模糊交叉耦合控制时的系统跟踪误差仅为0.045°。对比发现，本文所提出的控制算法确实可以有效减小系统跟踪误差，提高跟踪精度，对类似的工程设计有一定的参考价值。

5 结束语

针对精密跟踪雷达伺服系统中跟踪误差的问题，提出并设计了一种适用于二维跟踪雷达的变增益模糊交叉耦合控制算法，在仿真环境下搭建基于此法的二维跟踪雷达伺服系统的仿真模型，对比验证了该算法的有效性，最后在某型跟踪雷达平台上验证了该算法的工程可实现性。结果表明，所设计的控制算法能有效减小系统跟踪误差，提高雷达伺服系统的跟踪精度，在二维精密跟踪雷达伺服系统中具有广阔的应用前景。