基于长短期记忆网络的机械臂逆运动学解

周恒旭，何志敏，周 燕

(1.佛山科学技术学院自动化学院，广东 佛山 528225； 2.佛山科学技术学院电子信息工程学院，广东 佛山 528225)

0 引言

机械臂是融合了机械工程、电子技术、计算机技术和自动控制理论等多学科的技术设备。逆运动学的求解是机械臂领域中的重要问题之一，它关系着机械臂的运动分析、轨迹规划和编程控制等任务的进行，尤其是对于6自由度的连杆型机械臂，其逆运动学解最多有16组[1-3]，计算复杂，且不一定具有解析表达式。求解机械臂型机器人的逆运动学解有多种方法，常见有几何法、代数法和数值法。几何法和代数法可以求得解析解，故可称为解析法。解析解为一封闭形式的函数，因此对任一独立变量，可将其代入解析函数求得正确的相应变量，因此，解析解也被称为闭式解。求解闭式解一般比数值解快，且容易区分可能的解，但闭式解的缺点是不通用，对求解的机械臂有限制，需满足Pieper准则[4]才能具有逆运动学闭式解。有些特种机械臂构型为了扩大末端姿态调整范围，是不满足Pieper准则的。对于数值法，它不依赖于特定形式的运动学结构，但求解速度慢，函数构造复杂。

文献[5]提出一种旋量理论结合代数消元求解逆运动学，克服了运动学标定中存在的奇异性问题，但求解过程较为复杂。文献[6]提出一种四元矩阵和Groebner基的消元法，获得没有增根的一元16阶方程，但具体操作过于复杂。文献[7]采用雅克比矩阵伪逆矩阵解决了在奇异处无法求解的情况，但求解角度精度只能达到0.01°级别。文献[8]提出一种用粒子群优化结合BP神经网络求解逆运动学的方法，但关节角度误差达到0.1°级别，有待提升。文献[9]提出一种用人工神经网络求解逆运动学，并取得较好的效果。文献[10]采用一系列的生成对抗网络配合真实数据求解逆运动学和逆动力学，实验表明该方法可行且网络会根据不同的电机选择不同的网络参数。文献[11]采用神经网络求解7自由度机械臂的逆运动学。文献[12]展示基于神经网络求解逆运动学的三节机械臂能通过奇异点。除了串联型机械臂，并联型机械臂的运动学也可用神经网络求解[13]。

研究发现，求解机械臂的逆运动学方法主要是改进迭代法和消元法，但依然存在操作复杂和耗时长等缺点。近年来，深度学习被广泛地应用在图像识别和语音识别等领域。理论上，在训练好的深度神经网络上经过1次传播即可得到相关的映射结果。利用神经网络技术求解机械臂的逆运动学本质，是对机械臂工作空间中的笛卡尔坐标系与关节空间坐标系之间的映射，同时也是同种坐标系下时序值之间的拟合。另外在避免奇异点的问题上，一般采用2种方法：规划的路径尽量避开奇异点；优化机械臂逆运动学求解算法，保证奇异点范围内的伪逆解的稳定性。而神经网络求解逆运动学的结果是一种伪逆解。经过研究发现，基于长短期记忆网络(LSTM)求解机械臂的逆运动学的精度较高。在此，以UR5机械臂为研究对象，提出了一种机械臂逆运动学求解算法。

1 UR5机械臂运动学模型

1.1 UR5机械臂的正运动学

机械臂的运动学方程描述了机械臂的工作空间和关节空间之间的数学映射关系。UR5机械臂是典型的开放式链式结构，由6个关节连接各臂，6个关节输入角度为θ=[θ1,θ2,θ3,θ4,θ5,θ6]。UR5机械臂的D-H坐标系如图1所示。

图1 UR5机械臂的D-H坐标系

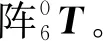
(1)

变换矩阵可被拆分成1个变换链：

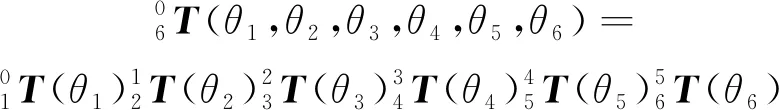
(2)

根据UR5机械臂的机械设计参数和关节之间的关系，建立能精确描述与实际的UR5拓扑结构相符的D-H表，如表1所示。

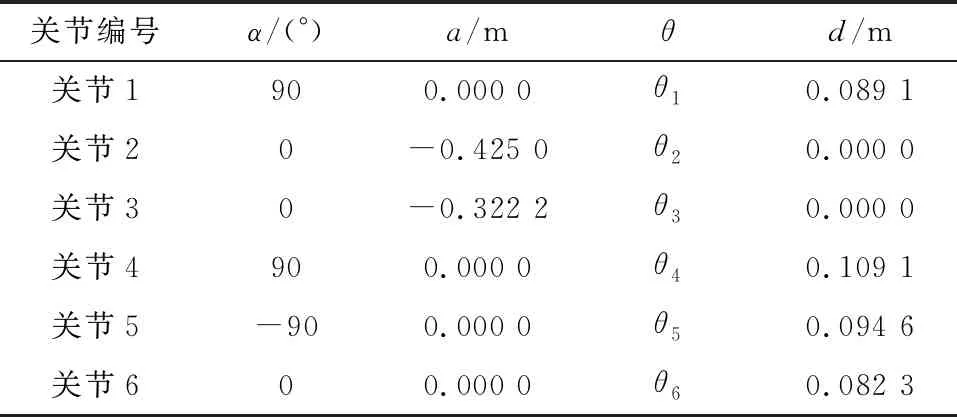
表1 UR5机械臂的D-H参数

表1中，α为机械臂的连杆转角；a为连杆长度；θ为关节角度；d为连杆偏距。

利用D-H参数为每个链接编写变换矩阵。臂i-1与臂i之间的变换为

(3)

1.2 UR5机械臂的正运动学验证

因后续的训练集是由MATLAB和robotics toolbox在UR5机械臂的工作空间中获取的，故必须验证MATLAB和robotics求解的正运动学数值是否与由式(1)～式(3)求出的数值一致。如果不对UR5机械臂的运动学模型进行验证，则无法说明UR5机械臂的参数是否有效，也无法获得有效可靠的训练数据集。随机取3组关节角度值(单位为弧度)：θa=[1,1,1,1,1,1]，θb=[2,1.5-1,1.2,-0.7,0.3]，θc=[1.2,-0.7,2.1,-0.3,0.5,-1.3]。将UR5机械臂的D-H参数与这3组关节角度值代入式(1)～式(3)，求得变换矩阵。其中，旋转矩阵用偏转角、俯仰角和回转角表示，即x-y-z欧拉角度。整理得UR5机械臂正运动学解如表2所示。

表2 UR5机械臂正运动学解

利用UR5机械臂D-H参数，在MATLAB与robotics toolbox环境下进行仿真验证，输入同样的3组关节角度，求得UR5机械臂位姿，即正运动解，如表3所示。

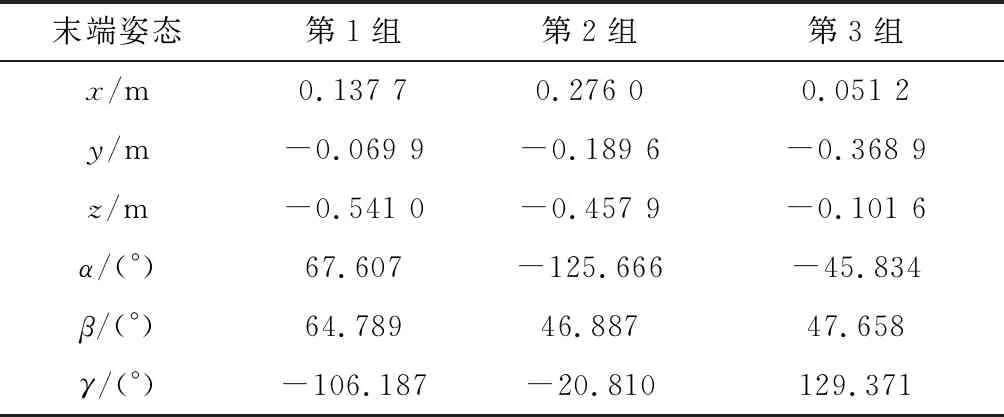
表3 仿真中的UR5机械臂正运动学解

目前，机械臂重复精度在±0.1 mm之间，绝对精度在±10 mm之间，故表中保留0.1 mm精度。对比表2和表3，发现根据公式获得的正运动学解与仿真环境得出的正运动学解非常接近，也意味着后续采集的数据集是有效的，同时也印证了UR5机械臂的运动学模型是正确的。

2 训练数据集获取

2.1 UR5机械臂的工作空间分析

机械臂的工作空间是指机械臂的末端执行器所能到达的三维空间范围。对UR5机械臂工作空间分析是获取准确训练数据集的前提，只有所有的训练集数据位于UR5机械臂的工作空间内，后续训练出的网络模型才具有实际应用意义。

主流的工作空间方法有解析法[14]、数值法[15]和图解法[16]，其中数值法中具有代表性的是蒙特卡洛法[17]。解析法操作烦琐，实际应用不推荐；图解法作图复杂，只适用于自由度较少的机械臂[18]；数值法是计算工作空间边界曲面上的点，其理论易理解，但准确性与取点及计算机速度有关[19]；蒙特卡洛法是通过大量随机的关节角度值，经过正运动学求解来获取到工作空间里所能到达的点，只要采样数据足够大，就能充分表示出整个工作空间，同时也有利于收集到大量与关节空间对应的工作空间的数据，即6个关节角度值对应其变换矩阵。故本文采用蒙特卡洛法收集训练数据集。

在MATLAB中配合robotics toolbox，利用已经建立好的UR5机械臂运动学模型，设置其关节限制角度：θ1=[-180°,180°]，θ2=[0°,90°]，θ3=[-90°,90°]，θ4=[-180°,180°]，θ5=[-90°,90°]，θ6=[0°,360°]。使用蒙特卡罗法，产生各关节的随机变量，使用ifine()函数计算正运动学解，蒙特卡洛随机采样点为30 000组，将UR5机械臂的工作空间可视化，如图2所示。

图2 UR5机械臂的工作空间

2.2 数据集的获取

记录每次随机的关节角度组和对应所求出的变换矩阵，使用robotics toolbox中的transl()函数，从变换矩阵中提取出位置矩阵再转置成1×3的位置矩阵，同时使用t2r()函数，从变换矩阵中提取3×3的旋转矩阵，再利用tr2rpy()函数将旋转矩阵转化为欧拉角。将位置矩阵、欧拉角和关节角度组保存下来，一共12维30 000组。

3 基于LSTM的机械臂逆解的求解

在深度学习领域里，主流的网络是卷积神经网络(CNN)与循环神经网络(RNN)。RNN网络能处理记忆信息，而其他类型的神经网络不能处理记忆信息，该特性在时序预测上至关重要，因为时序信息跟前后内容相关。另一方面，对于机械臂，其运动过程是一种时序过程，且前后每个关节的空间变化是相关的。利用RNN网络，进行机械臂的笛卡尔坐标系与关节空间坐标系的映射和对应数值拟合预测是可行的。但是由于RNN网络有梯度消失的问题，难处理长序列的数据，为了解决这一难题，一种时间循环神经网络，即长短期记忆网络(LSTM)被研究出来[20]。各类LSTM网络在数据预测方面有着较广泛的应用，如交通流预测和故障预测等[21-22]。

3.1 LSTM网络的训练

在时序预测和数据拟合方面，LSTM网络已经成为主流的方法之一。LSTM是一种含有LSTM区块的神经网络。LSTM区块如图3所示，包含输入门、遗忘门和输出门，以及与隐藏信息状态形状相同的记忆细胞单元，从而记录额外的信息。其中，C同时为控制参数，决定着信息的保留或遗忘，σ是一种门，决定着信息通过的方式，使用Sigmoid函数实现该功能的计算。多个LSTM区块的连接再配合一些隐含层和全连接层即可组成LSTM网络。

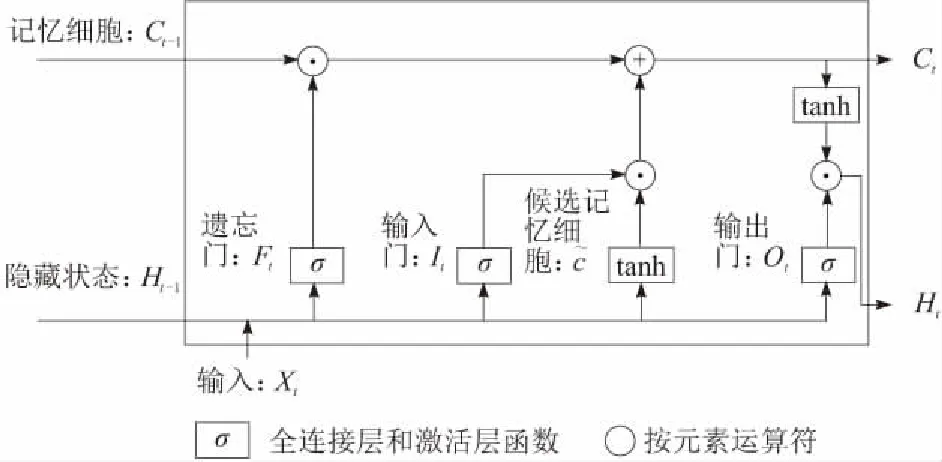
图3 LSTM区块

利用之前获得的12维30 000组数据集输入网络进行训练，数据集前25 000组为训练集，余下的5 000组为测试集。输入数据为机械臂的工作空间的数据[x,y,z,α,β,γ]，标签数据为关节空间的数据[θ1,θ2,θ3,θ4,θ5,θ6]。

在进行训练前，需对数据进行标准化处理，标准化后的数据的均值为0、标准差为1。因训练数据既有位置数值也有角度数值，标准化是为了避免某个维度的特征重要程度过大或过小，使得数据集里的异常点影响降低。标准化处理的操作如式(4)所示：

(4)

对于式(4)，是对每1列进行操作，mean为平均值，σ为标准差。

为了准确评价预测求解模型的有效性，对每一列的关节数据采用均方误差(MSE)来评价指标评判模型的预测效果。如式(5)：

(5)

f(x)为网络模型预测的关节角度；y为实际关节角度值；n为样本数。

训练参数设置为：BATCH_SIZE 为30；隐含层单元CELL_SIZE 为10；学习率LR为0.001。重复进行10次训练实验，记录每1次训练过程中的训练误差和测试误差求平均，绘制训练和测试过程误差如图4所示，每轮迭代后会使用测试集的数据计算模型的MSE。

图4 训练和测试过程的误差损失

图4中，实线表示训练过程的MSE变化趋势，虚线表示测试过程的MSE变化趋势。对于训练过程，在迭代400次时，误差损失从32降低到2左右，在3 000次时，误差损失达到0.000 5级别时，之后误差损失并不会出现明显大幅的下降。对于测试过程，在迭代500次前，测试的MSE趋势不稳定。随着训练的增加，测试的MSE不断下降，在迭代次数在1 500次之后时趋于平稳，其MSE稳定在0.005级别。考虑到这些数据是标准后的数值，0.005级别精度也已经达到关节角度的分单位级别，完全满足机械臂运动精度要求。

LSTM模型训练后，接着使用测试集进行预测网络的测试。以机械臂第1个关节为例，其测试预测效果如图5所示。图5中，实线为LSTM网络预测的值，虚线为实际值，纵坐标表示标准化处理后的关节值，横坐标表示5 000组测试集的前60组数据。由图5可知，实线与虚线基本完全重合，意味着LSTM网络预测的值十分接近实际值，说明了训练达到预期效果。同时通过程序查看，可知预测求解值和实际值之差在0.001级别。

图5 机械臂第1关节的实际值与LSTM预测值对比

3.2 LSTM网络的性能对比与分析

单纯分析网络模型训练后的求解结果，只能说明预测求解精度满足机械臂运动要求，这并不能完全体现长短期神经网络求解逆运动学的优势。故继续对本文所提出的LSTM求解法的进行精度和速度的性能测试。本次实验硬件为Intel i5-8300H和NVIDIA GTX 1050Ti。

在精度性能方面，对LSTM网络使进行10次训练并测试，统计计算其MSE，与经典的BP网络与RBF网络相互比较，参考文献[23]的结果，绘制结果对比表，如表4所示。

表4 3种网络求解结果对比

据表4分析得知，LSTM的精度远大于BP网络与RBF网络。一方面这得益于LSTM网络在长段数据拟合方面有着得天独厚的优势；另一方面BP网络与RBF网络存在预测极限的问题，当到达预测极限时，随着训练的提高，预测效果反而下降，即过拟合现象。

在速度性能方面，对于传统解法，根据式(1)～式(3)编写求解UR5机械臂逆运动的代码，使用语言为Python。对于LSTM网络求解法，通过载入之前训练好的模型文件。2个方法输入相同的变换矩阵，记录2种方法得出6个关节角度值的时间，进行20次实验，绘制成对比图，如图6所示。圆点表示公式求解耗时；星号点表示LSTM求解耗时。对20次实验进行加权平均，得出公式求解平均耗时为0.405 2 s，LSTM求解平均耗时为0.229 8 s。这说明了LSTM求解方法快于传统的公式求解法。LSTM求解法耗时约等于传统公式求解法的一半。

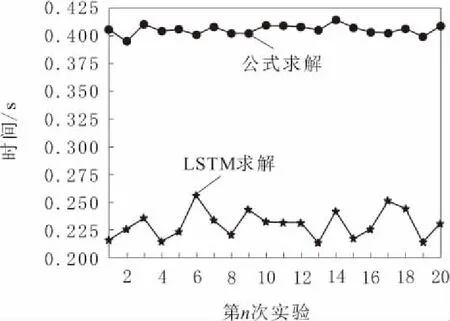
图6 公式求解与LSTM求解耗时对比

4 仿真实验

为了进一步验证LSTM网络的求解效果。将在机器人仿真器CoppeliaSim上进行仿真实验。CoppeliaSim是机器人仿真软件，基于分布式控制结构，可以通过嵌入式脚本、插件、ROS或远程客户端控制每个对象模型，使得CoppeliaSim通用。

实验使用MATLAB编写代码与CoppeliaSim进行通信和联合仿真，MATLAB负责将LSTM模型求解的逆运动学解的结果传递给CoppeliaSim里的UR5机械臂，并控制UR5机械臂进行仿真运动，具体的实验流程如图7所示。

图7 MATLAB与CoppeliaSim联合仿真流程

4.1 直线运动仿真

在UR5工作空间上选取直线路径点(有多段直线组成路径)，路径点同时也为机械臂在某时刻的末端姿态。路径点的具体数值如表5所示。

表5 直线路径点的数值

经过LSTM求解后，将获得对应的逆运动学结果传递给由CoppeliaSim控制的UR5机械臂，使UR5机械臂进行直线运动。机械臂的末端运动轨迹用黑色轨迹显示出来，如图8所示。

图8 UR5机械臂的直线运动

记录UR5机械臂运动过程的关节角度变化数值，并绘制曲线图，如图9所示。

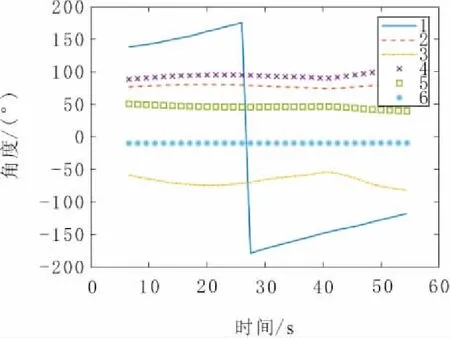
图9 UR5机械臂直线运动时各关节角度变化

在图9中，1表示第1个关节的角度，2表示第2个关节的角度，以此类推。由图9可知，除了第1关节外，其他关节变化平缓，这是由于选取的直线路径有个折线拐弯，围绕着UR5机械臂拐弯，所以第1关节角度出现反转变化。总体而言，仿真运动轨迹跟选取的轨迹基本一致，直线部分没有明显的抖动，证明了LSTM模型求解结果的准确性。

4.2 圆弧运动仿真

在UR5工作空间上选取圆弧路径点，路径点的具体数值(部分)如表6所示。

经过LSTM求解后，将获得对应的逆运动学结果传递给由CoppeliaSim控制的UR5机械臂，使UR5机械臂进行圆弧运动。机械臂的末端运动轨迹用黑色轨迹显示出来，如图10所示。

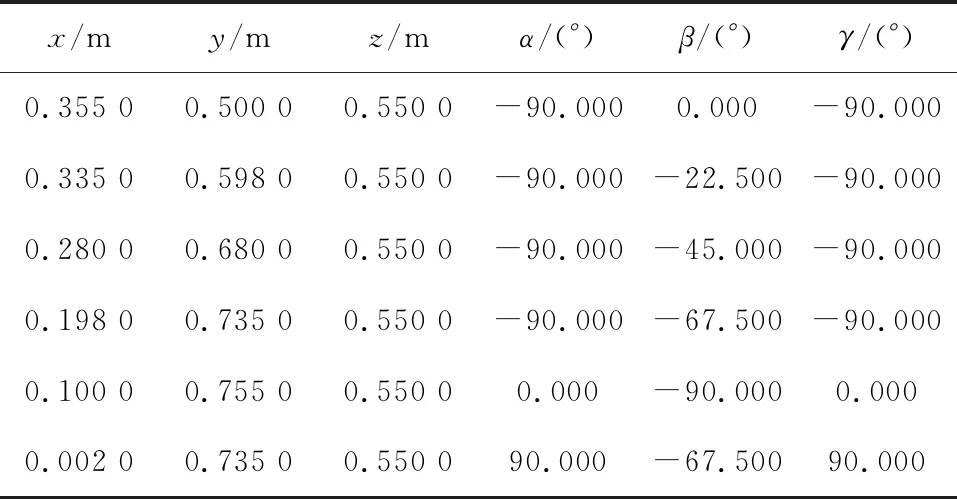
表6 圆弧路径点的数值(部分)

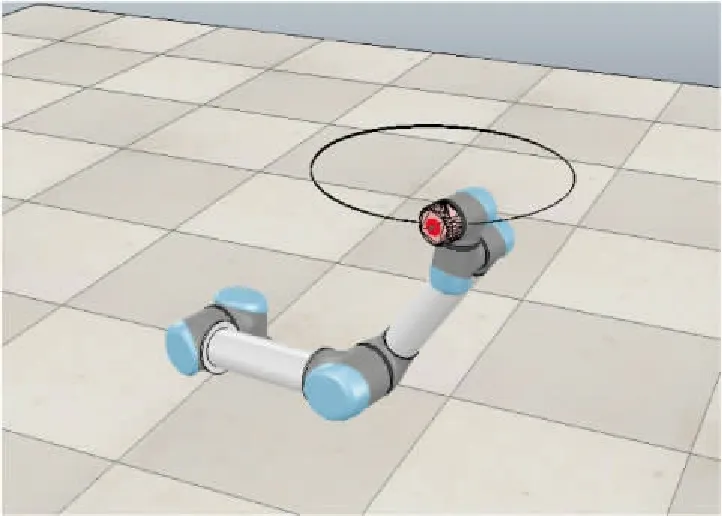
图10 UR5机械臂的圆弧运动

记录UR5机械臂运动过程的关节角度变化数值，并绘制曲线图，如图11所示。

图11 UR5机械臂圆弧运动时各关节角度变化

在图11中，1表示第1个关节的角度，2表示第2个关节的角度，以此类推。由图11可知，除了第1个关节外，其他关节变化平缓，这是由于选取的圆弧路径经过UR5机械臂的0坐标系的y轴，故在进行完整的圆弧路径运动时，第1个关节角度出现反转变化。总体而言，仿真运动轨迹跟选取的轨迹基本一致，弧线部分没有明显的抖动，证明了LSTM模型求解结果的准确性。

5 结束语

本文提出了基于长短期记忆网络的机械臂逆运动学求解算法。通过研究及实验发现，基于LSTM求解机械臂逆运动学解具有很高的精度，结合3.1节分析和表4，关节角度误差控制在分单位级别，完全满足实际的使用需要，同时避免了传统公式求解法的复杂操作使用过程。实验结果显示LSTM运算速度快，求解法耗时约等于传统公式求解法的一半。另外，LSTM拥有记忆功能以记忆每个关节之间的变换规律，故相比于其他网络有较高的精度。由CoppeliaSim的仿真实验可知，仿真运动轨迹跟选取的轨迹基本一致，弧线部分没有明显的抖动，证明了LSTM模型求解结果的准确性。