水下机械臂运动空间分析与轨迹跟踪算法优化
2020-07-01樊智敏哈振骞薛福峰王明凯
樊智敏,哈振骞,薛福峰,王明凯
(青岛科技大学机电工程学院,山东 青岛 266061)
0 引言
随着海洋开发与研究蓬勃发展,无人航行器搭载机械手在进行水下打捞、援潜救生、海底设施维护与装置回收、海底生物及岩石标本的采样等方面得到了越来越广泛的应用。目前,发展趋势是研制适合多种水下作业的航行器,而其末端执行器(机械臂)或手爪是水下作业航行器执行作业的关键部分[1-3]。相比陆地上的移动机械臂和空间机械臂,水下机械臂容易受到海浪、波浪和洋流等环境的干扰,使末端执行器不能达到预期位置。由于水下机械臂运动的不确定性,导致在运动过程中受力方向也各不相同,再加上多种不可预见的外界干扰,在建立水下机械臂动力学模型时,需要充分考虑各种水动力的影响以及各力之间的耦合[4]。因此,在水下机械臂的控制器设计中要考虑到运动非线性、受到的干扰力不确定等特点。
蒙特卡洛法是通过D-H法则建立机械臂的关节变量与工作空间的映射关系,再通过正解运动学方程得到坐标值,这些坐标值的集合组成了机械臂的工作空间[5-9]。此方法为研究水下机械臂的工作空间提供了理论基础。
水下机械臂具有高度非线性、强耦合性和多输入多输出的时变性等特点,常规的线性控制方法不能满足控制要求。赵克楠[10]提出模糊PID控制方法,通过模糊规则调节PID控制器参数,实现参数根据位置误差和位置误差变化率的动态调节;Londhe等[11]将水下机械臂位置误差和位置误差变化率输入到模糊PID控制器中,进行参数的优化;Filaretov等[12]采用多链路的方法对水下机械臂运动进行补偿,实现水下机械臂运动的自动校正;Barbalata等[13]采用低水平位置/力控制结构,结合流体动力学提出一种在没有力-扭矩传感器情况下计算末端执行器之间相互作用力的方法;陈显婷等[14]采用模糊控制与CMAC控制方法相结合的复合控制策略,对水下机械臂进行控制;邱红祥[15]设计基于固定增益的PD控制器,将机械手空载作业下的参数作为固定增益的作业参数,以此满足系统的稳定性;王亚猛[16]用PWM高速电磁开关阀和具有抑制水液压缸摩擦力影响的鲁棒控制器控制水液压缸,以驱动具有3个自由度两关节的机械臂。上述研究都是通过改进误差进行的优化设计,水下环境复杂,对外界干扰无法预测,可能导致误差较大。本文提出一种基于RBF神经网络的鲁棒控制算法,针对干扰项的不确定模型进行逼近,提升水下机械臂的控制性能。
1 工作空间分析
1.1 水下机械臂运动学分析及仿真
本文研究的水下机械臂主要包括6个旋转关节和1个末端水下机械手,如图1所示。

图1 水下机械臂结构
为了描述相邻杆件之间的关系,基于D-H法则对水下机械臂进行建模。D-H法则描述相邻杆件之间坐标系之间的关系如图2所示。其中,i(i=1,2,3,4,5,6)为关节数;ai为沿着Xi轴从Zi移动到Zi+1的距离;αi为绕着Xi轴从Zi转到Zi+1的角度;di为沿着Zi轴从Xi-1到Xi的距离;θi为绕着Zi轴从Xi-1到Xi的角度。表1是基于D-H法则各连杆的参数表。其中,假设第4节和第5节质心重合,两者坐标系原点重合。

图2 D-H法则相邻连杆坐标系关系
表1 水下机械臂各连杆参数

θidi/mmαi-1/(°)ai-1/mmθimin/(°)θimax/(°)θ112600-6060θ29390930120θ37930793-6060θ4633-900-180180θ5900-9090θ6457-9000360
机械臂的运动学分析是机械臂研究的前提,是机械臂工作空间分析和运动控制的基础。根据连杆参数和D-H法则建立的坐标系,机械臂相邻关节坐标系i-1和i之间位姿变换矩阵为
(1)
式中,cθi=cosθi,sθi=sinθi,cαi-1=cosαi-1,sαi-1=sinαi-1。
将各个关节位姿矩阵依次相乘,便可得到机械臂末端的位姿矩阵为
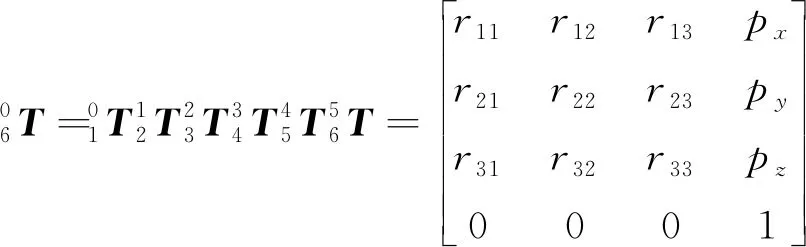
(2)
[pxpypz]T为末端执行器相对基座坐标系的位置向量;[r11r21r31]T,[r12r22r32]T和[r13r23r33]T为末端执行器相对基座坐标系的位姿向量。
1.2 水下机械臂工作空间分析
描述水下机械臂的工作空间,可以不用考虑末端执行器位姿的关系,所以根据水下机械臂的运动学正解,可以求出水下机械臂的位置向量[pxpypz]T。根据各个关节限位在MATLAB中利用Rand函数得到随机值,将随机值代入到运动学正解方程中,得到相应点的位置向量,最后得到水下机械臂的工作空间云图,如图3~图6所示。
由图4~图6可知,水下机械臂的工作范围为x∈[-1 250,1 500],y∈[-1 500,1 500],z∈[-1 000,1 250];水下机械臂的工作空间近似一个椭球体,空间符合各个关节实际运动空间,模拟出的工作空间结构紧凑,能够真实地描述水下机械臂的工作空间。
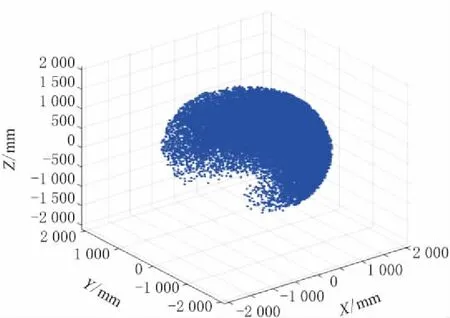
图3 水下机械臂运动空间云图
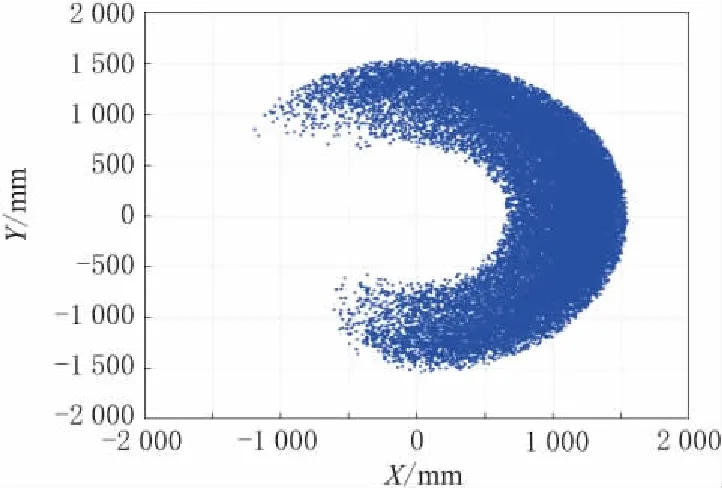
图4 XOY面运动空间云图

图5 XOZ面运动空间云图

图6 YOZ面运动空间云图
2 水下机械臂的轨迹跟踪控制
关节空间轨迹跟踪是给定机械手各个关节的驱动力和力矩,严格地控制各个关节的运动轨迹,使各个关节的速度和位移等状态量能够跟随理想的运动轨迹。水下机械臂是一个复杂的多输入多输出的非线性系统,建立的动力学模型必然存在着不确定性,传统的控制算法难以得到理想控制效果。本文采用基于HJI理论的RBF神经网络自适应控制算法,并以双关节水下机械臂为例验证该控制算法的有效性。
2.1 水下机械臂轨迹跟踪控制
水下机械臂的动力学模型为
(3)

定义理想跟踪轨迹为qd,跟踪误差为e=q-qd,反馈控制律为u,则设计前馈控制律为
(4)
将式(4)代入式(3)中,可得闭环系统式为

(5)
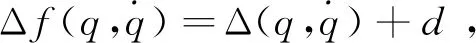

(6)
采用RBF神经网络逼近Δf,其表达式为
(7)
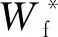
将式(6)和式(7)联立可得
(8)
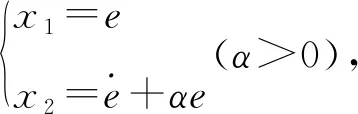
(9)

利用HJI不等式将式(9)改写为

(10)
d=εf
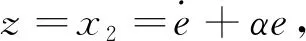
对系统式(9)设计如下自适应律:
(11)
设计反馈控制律为
(12)
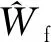
最后可以得出闭环系统式(5)满足J≤γ。可以利用Lyapunov函数验证分析该控制方法的稳定性,在这里不过多赘述。
2.2 仿真与分析
根据文献[18]中对于水下二自由度水下机械臂动力学模型和实验研究,可以得到水动力摩擦系数CD和附加质量系数CA一般取常数,通常情况下取值为CD=1.1和CA=1。考虑到实际控制中可靠性和简单性原则,一般的水下机械臂连杆长度大多小于2 m,此时水下机械臂水动力分析主要对重要组成部分进行补偿。这里对二自由度水下机械臂水动力项取近似表达式为
(13)
基于HJI理论的RBF神经网络自适应控制器的有关参数为:α=20,γ=0.005,ci=[-1.5,-1,-0.5,0,0.5,1,1.5] ,bi=10,其中涉及到自适应律的η=1 500。
取机械臂参考值:m1=15 kg,m2=15 kg,l1=1 m,l2=1 m,r1=0.5 m,r2=0.5 m,g=9.8 m/s2,其中r1,r2为机械臂中点长度值。根据这些参数,对二自由度水下机械臂在不同作业情况下的运动情况进行分析。
2.2.1 基于水动力作用下轨迹跟踪控制

通过水下机械臂相关参数设定,结合该控制器控制效果的仿真结果进行分析,如图7所示,水下机械臂两关节通过初始阶段的调整后,均能较好地跟踪既定角度,且有较高的控制精度和较快的响应时间。控制器响应时间较快,0.1 s内即完成了调整准备工作,其中关节1能够以±0.002 rad的精度跟踪角度,具有较好控制效果。相比关节1而言,关节2的耦合项较少,其控制效果更好,关节2的控制精度近乎为0。两关节均表现出了较好的跟踪性能。

图7 水下机械臂角度跟踪曲线(无干扰)
机械臂两关节角速度跟踪效果如图8所示,各关节的起始速度为0,速度跟踪效果较好,能够依照设定速度完成跟踪,未出现速度突变情况,控制效果良好。跟踪角速度误差较小,可以忽略角速度变化,因此能够较为平顺地完成作业任务。
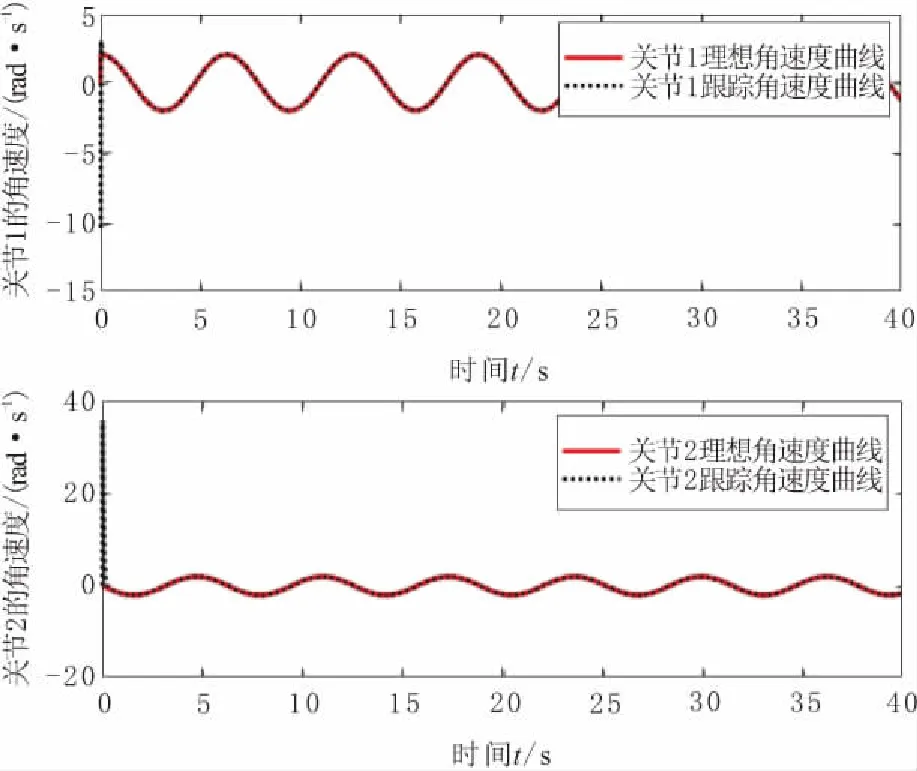
图8 水下机械臂角速度跟踪曲线(无干扰)
水下机械臂运动时会受到水动力力矩影响,本文采用近似表达式模拟水动力作用对水下机械臂的影响,机械臂运动时各关节均会受到水流影响,其影响也与机械臂的运动速度和尺寸相关联。由于只考虑水动力的作用,并未将系统模型的不确定性和外界干扰考虑在内,此时所涉及的RBF神经网络控制器逼近对象为机械臂关节受到的水动力力矩。仿真结果如图9所示。不考虑初始调整阶段,关节1逼近的水动力力矩效果较差,究其原因是由于关节1耦合项较多影响较大,但根据角度跟踪效果和速度跟踪效果来看,也实现了对关节1的补偿控制;关节2逼近的水动力力矩效果较好,可以实现对关节2的补偿控制。总体来说,在只考虑水动力作用因素影响下,所设计的控制器能够较好实现补偿任务,控制表现良好。

图9 控制器逼近水动力曲线
2.2.2 基于模型不确定性和外界未知干扰下轨迹跟踪控制
针对系统模型不确定性作如下假设:假设模型不确定性部分作为外界干扰力矩输入到系统中,与水动力共同作用分别施加到关节1和关节2上。设关节1和关节2的模型不确定性和外界干扰的总干扰假设为
(14)
基于模型不确定性和外界干扰下的水下机械臂角度跟踪效果如图10所示,关节1和关节2有不俗的跟踪效果。
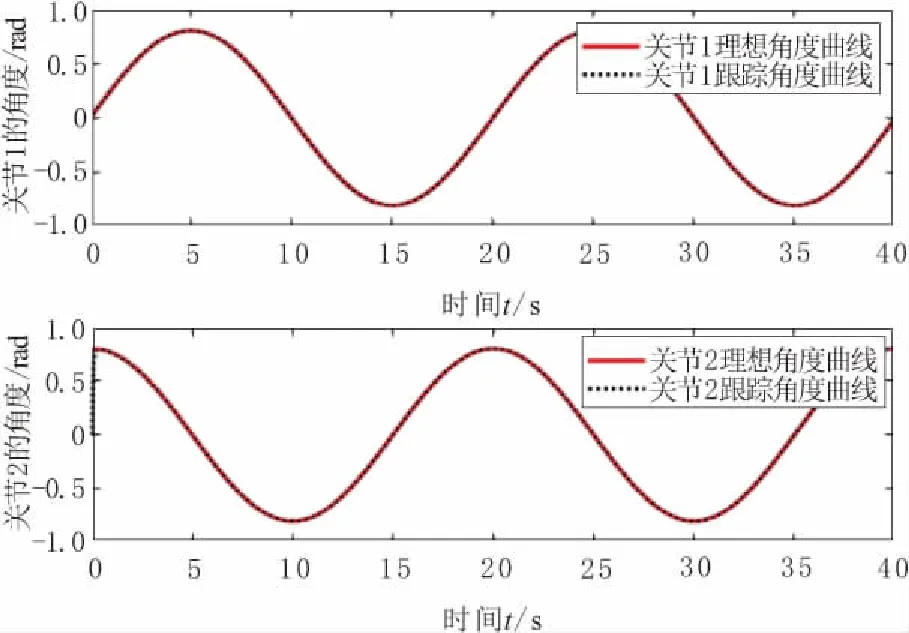
图10 水下机械臂角度跟踪曲线(有干扰)
结合跟踪误差图11所示可知,关节1的跟踪误差有微小波动可忽略,关节2表现出更好的控制效果,表现出控制器良好的控制跟踪特性。角速度跟踪效果如图12所示,关节1和关节2角度的跟踪均表现良好跟踪效果,未出现明显尖角由此证明能够平稳完成跟踪任务。通过神经网络控制器的逼近能力,对水下机械臂系统模型不确定性和未知外界干扰进行逼近,逼近效果如图13所示。由图13可知,关节2的逼近效果明显要优于关节1的逼近效果,这是因为在关节1处参数的耦合效应更明显;根据角度跟踪效果和角速度跟踪效果来看,关节1处也能实现逼近效果并完成补偿任务,关节2处也有不错的逼近效果。由此证明该控制器能够逼近系统模型不确定性和外界不确定干扰,并且能够完成对水下机械臂系统的补偿任务,有较好的控制性能。
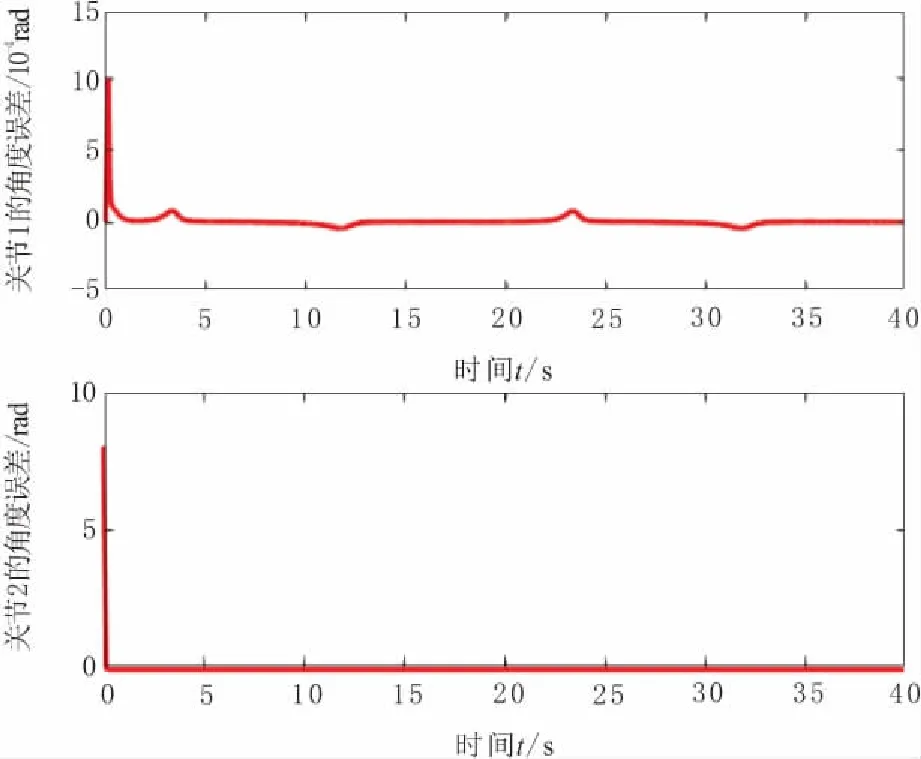
图11 水下机械臂角度跟踪误差(有干扰)

图12 水下机械臂角速度跟踪曲线(有干扰)

图13 控制器逼近外界总干扰曲线
水下机械臂关节1和关节2的运动规律关系到末端执行器的运动轨迹,由水下机械臂系统的坐标可以得到机械臂在垂直面坐标表达式为
(15)
根据设定的初始值与机械臂运动规律可知,水下机械臂末端执行器初始坐标为(x(0),z(0))=(0.99,0)。将仿真结果转换到末端执行器的运动轨迹如图14所示。由图14可知,在开始阶段运动轨迹是有较大的偏差,这是因为控制器处在调整期,属于系统正常误差范围,进入稳定期后跟踪轨迹基本与理想轨迹重合,跟踪效果良好,在交汇点也未出现跟踪错误,能够正确跟踪轨迹,印证该控制器良好的控制效果。
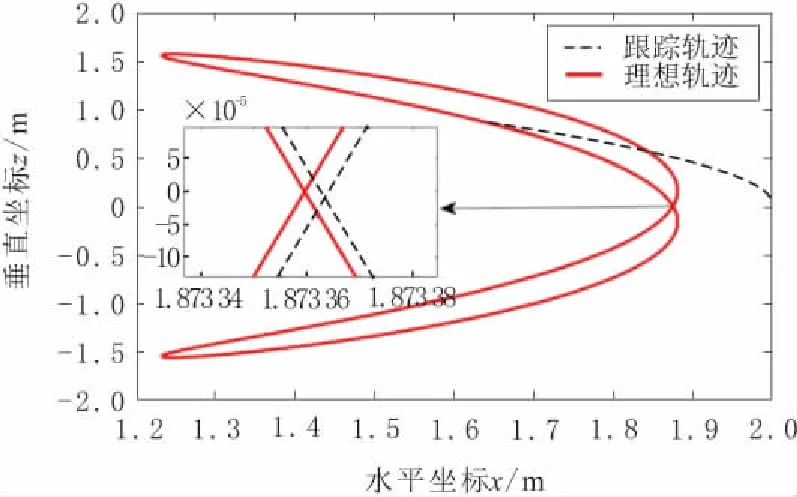
图14 机械臂末端轨迹跟踪效果
无论是水动力的影响,还是模型不确定性或外界未知干扰的影响,该控制器均表现出较好的控制效果,通过末端执行器的跟踪轨迹验证,证明本文所设计的基于HJI理论的RBF神经网络自适应控制器具有良好的鲁棒性。
3 结束语
通过对水下机械臂的运动学分析,设计基于HJI理论的RBF神经网络自适应控制器,并进行仿真验证。
以六自由度水下机械臂为例,基于D-H法则分析了机械臂的运动学,通过仿真验证了其正确性,通过MATLAB构建了水下六自由度机械臂的运动空间云图,真实体现水下机械臂的运动空间。
针对水下机械臂模型不确定性和外界未知干扰的问题,提出基于HJI理论的RBF神经网络自适应控制方法,以水下二自由度机械臂为例进行验证分析。在无外界干扰情况下控制器能够很好逼近水动力力矩曲线,对机械臂施加控制补偿。
为进一步确认控制器的控制效果,在水动力作用和系统模型不确定性及未知外界干扰共同作用情况下验证该控制器,控制器表现出优良的控制性能,具有较强的控制鲁棒性。
