EMA数字伺服驱动系统无差拍电流预测控制研究

孙 磊，赵东标，张 瑶，刘豪志

(南京航空航天大学机电学院，江苏 南京 210016)

0 引言

机电作动器(electro-mechanical actuator，EMA)作为功率电传技术的重要实现形式，是机载作动系统发展方向之一，在航空航天领域具有广阔的应用前景[1-2]。

伺服电机是EMA系统的控制核心，其动静态性能决定着EMA 的整体性能[3]。本文选用永磁同步电机(permanent magnet synchronous motor，PMSM)作为系统的驱动电机，采用经典的三环级联控制结构。电流环作为最内环，是高性能EMA伺服驱动控制系统设计的关键。目前，在PMSM伺服系统中应用的电流环控制策主要为滞环控制[4]、PI控制[5]和预测控制[6-7]。滞环控制响应速度快，但存在开关频率变化大，稳态时电流纹波大等缺陷。PI控制结构简单且稳定可靠，但参数鲁棒性差，在较宽调速范围下无法同时兼顾响应的快速性和稳态的高精度。无差拍预测控制相比于前2种传统控制策略，开关频率恒定且具有更好的动态性能和更小的谐波分量，更适用于有着快速响应以及高精度要求的EMA系统。但预测控制依赖于精确的电机模型，当电机受温度等因素的影响，参数发生变化时，预测控制的电流稳态误差增大，系统性能显著降低。此外，数字控制中存在的采样延时、逆变器非线性等固有缺陷，制约着伺服控制性能的进一步提升。针对上述问题，本文研究设计了一种EMA数字伺服驱动系统的电流环控制器。

1 EMA伺服驱动控制系统模型

1.1 EMA机械传动结构模型

如图1所示，该EMA机械结构主要包括电机轴、离合器、轴承、滚柱丝杠副和推杆。在工作状态下，离合器结合，永磁同步电机驱动滚柱丝杠副将旋转运动转化为推杆的直线运动，从而对末端舵面、起落架等装置有效作动；在非工作状态或发生故障时，离合器脱开实现对系统的保护[8]。

图1 EMA机械传动结构

采用经典的弹簧-质量-阻尼模型对机械结构进行模型简化等效[9]。根据如图2所示的动力学等效模型，可得到机械结构的运动平衡方程与转矩方程为

(1)

Tm，θm分别为电机输出端转矩、转角；Kd，Jd和ζd分别为系统等效的扭转刚度、负载转动惯量和阻尼系数；Td，θd分别为丝杠端的转矩、转角。

图2 EMA机械结构等效动力学模型

经拉氏变换及计算，可得丝杆螺杆的转角θd关于电机转角θm的传递函数为

(2)

转角θd乘以丝杠副传动比，即可转换为推杆末端最终的线性位移x(s)：

(3)

ph为丝杠导程。

1.2 EMA伺服控制系统模型

EMA伺服控制系统主要由控制器、逆变器和永磁同步电机构成[10]。控制器以DSP+CPLD为核心，在接收上位机的位置指令和收集来自传感器的信息后，实现逻辑功能并生成PWM信号。基于IGBT的逆变器在PWM信号下，将270 V航空直流电源电压转换为PMSM的三相控制电压电平。在三相电作用下，PMSM输出用于驱动机械结构的电磁转矩，附有的霍尔传感器和旋转变压器反馈实时电流、速度和位置信息。

控制器通常采用id=0矢量控制技术结合对应于三相电压源逆变器的SVPWM技术，在结构上为位置-速度-电流三闭环，如图3所示。

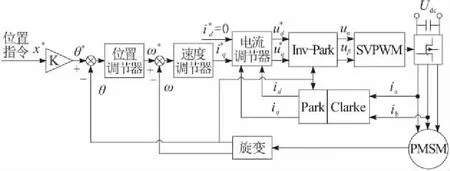
图3 EMA三闭环伺服驱动控制系统原理

PMSM作为被控对象，其模型的建立是控制器设计的前提。本文研究的EMA选用表贴式三相永磁同步电机，为方便控制器设计，假设PMSM为理想电机，选取同步旋转坐标系d-q轴下的数学模型，其定子电压方程可以表示为[11]

(4)

ud，uq为定子交直轴电压分量；id，iq为定子d-q轴电流分量；R为定子电阻；Ld=Lq=L为d-q轴电感分量；ψ为永磁体磁链；ωe为转子电角速度。

2 EMA伺服控制系统电流预测控制器设计

本文设计的电流预测控制器由无差拍控制、非线性补偿和参数辨识3部分组成，整体结构如图4所示。

图4 电流无差拍预测控制器结构

2.1 无差拍控制

根据式(4)，选择d-q轴电流作为状态变量，可得PMSM连续状态空间函数为

当前农村正处于转型期，传统农业向现代农业转型，旧农村向新农村转型，传统城镇化向新型城镇化转型。如何直面转型期间暴露的弊病并及时改进，成为亟待解决的问题。在乡村居住形态变迁方面，必须认识到加强对农村精神文明引导的重要性。习近平强调“房子是用来住的”，农村房屋更应发挥基本生活保障功能而不是攀比炫耀功能。要弘扬社会主义核心价值观，倡导脚踏实地的简朴生活作风，通过精神引导打压农村的炫耀攀比风气，减轻因注重房屋外在效果而带给农民的负担。因此，在乡村转型过程中，必须重视农村居民居住形态变迁的情况，做出合理规划，更好地促进农村发展。

(5)

为在微处理器DSP中实现数字化控制，假设电流采样周期足够小，采用一阶泰勒公式对式(5)离散化处理，可得如式(6)所示的无差拍预测控制离散电机模型：

i(k+1)=A(k)i(k)+Bu(k)+C(k)

(6)

根据式(6)和k时刻的采样电流值，可预测当前k时刻所需施加的参考电压值，从而使k+1时刻的实际电流可以无差拍跟踪k时刻的参考电流值，即

i*(k)=i(k+1)

(7)

i*(k)为电流期望值。

根据式(6)和式(7)，可得控制器k时刻参考控制电压为

u(k)=B-1[i*(k)-A(k)i(k)-C(k)]

(8)

然而在数字控制中，由于处理器计算时间和传感器采样时间等因素的影响，控制电压更改的执行滞后于实际电流的变化。为避免此类固有延时影响控制器性能，在无差拍预测控制中引入一拍延时补偿。即在第k时刻根据采样电流值预测k+2时刻的电流值，从而计算出k+1时刻的控制电压，经过一拍延迟执行该电压值使得k+2时刻的实际电流值等于参考值。电流一拍延时的计算公式为

i(k+2)=A(k+1)i(k+1)+Bu(k+1)+

C(k+1)

(9)

2.2 非线性补偿

逆变器在实际应用中并非处于理想状态，功率管压降、IGBT开关延时和死区时间等非线性因素会导致逆变器输出电压产生畸变，影响系统的控制精度和稳定性[12]。本文采用基于伏秒平衡原理的平均电压补偿法对畸变电压进行补偿，故可将文献[13]中一个PWM周期内平均畸变电压计算公式简化为

(10)

由于无差拍电流控制器是在同步旋转坐标系下，运用傅里叶变换将ΔV转换为d-q轴的畸变电压Δu，即

(11)

(12)

式(11)和式(12)中，畸变电压包含六次、十二次和更高次的谐波分量。根据电流极性及速度大小，选取其中影响因素大的六次和十二次谐波分量作为补偿，最终用于SVPWM模块的控制器输出电压为：

(13)

(14)

(15)

2.3 参数辨识

在EMA系统工作过程中，温升、磁饱和等因素会造成PMSM参数的改变。电机参数的变化会导致无差拍电流预测控制器模型参数与实际参数的不匹配，降低系统运行性能。为减小电机实际参数值摄动对控制器的影响，本文选用带遗忘因子的递推最小二乘法辨识电机参数。根据文献[14]可将回归模型写为

(16)

电机稳态模型为二维方程组，如果采用1个RLS算法模块同时辨识电阻、电感和磁链3个参数，方程组欠秩，辨识结果可能不唯一。根据文献[15]中参数敏感性分析，虽然电阻偏差会同时改变d-q轴电流，但由于电机绕组阻值一般较小，电阻变化影响较小可忽略不计，故本文在辨识时假设电阻值固定不变。在此基础上，根据式(6)和式(16)可得电感与磁链的递推算法为

(17)

3 模型仿真与分析

参照第1节中EMA整体结构，在MATLAB/ Simulink仿真环境下分别搭建基于PI电流控制器、PI前馈解耦电流控制器，以及第2节设计的无差拍电流预测控制器的EMA三环控制器+机械结构的仿真模型。为便于对比，3个模型的位置环控制器均采用系数值相同的P控制，速度环控制器均采用系数值相同的PI控制。各比例、积分系数通过电机参数计算所得，电机主要参数如表1所示。

表1 电机参数

采样和计算延时通过单位延时模块实现，EMA系统所用IPM开关管为大功率，由相关手册通过Simulink开/关延时模块设置死区时间为4 μs。机械结构部分由传递函数模块实现，其相关参数值经计算后如表2所示。RLS辨识算法初值设为P(0)=αI，α=1×10-3，x(0)=[0.002 7 0.069 33]T，遗忘因子λ通常在0.95～1之间，本文设为0.98。

表2 机械部分相关参数

仿真时在0.01 s给定10 mm的位置指令，电机负载转矩为机械结构部分按式(1)计算所得的电机轴输出端转矩Tm。图5为EMA系统的位置响应曲线图，图中DPC为无差拍预测控制；图6为3种电流控制器下部分时间的三相电流波形图；图7为电机参数辨识结果图。

图5 位置响应对比曲线

图6 3种电流控制器下的三相电流波形

由图5可知，基于无差拍电流预测控制器的EMA系统位置阶跃响应时间为0.275 s，稳态误差为0.018 mm，而基于PI前馈解耦电流控制器和PI电流控制器的响应时间为0.281 s和0.283 s，稳态误差为0.031 mm和0.035 mm。对比可见，无差拍电流预测控制器响应速度更快的同时响应精度更高,保证EMA系统更为精确地跟踪位置轨迹。

由图6a，6b，6c对比可知，PI前馈解耦控制的三相波形相较于PI控制虽然更为平滑，但仍存在逆变器非线性引起的电压畸变。引入非线性补偿的无差拍电流预测控制器在改善d-q轴电流解耦特性的同时，能够有效降低由死区时间导致的零电流钳位的影响，使三相波形更趋近于理想的正弦。

图7 电机参数辨识曲线

由图7中电感和磁链的辨识结果可知，在0.01 s电机初始启动阶段，由于电流的突变导致辨识误差较大，随后基于RLS的参数辨识值快速收敛到实际值。最终电感辨识值与实际值误差约为4.1%，磁链辨识值与实际值误差约为2.4%。整个辨识过程在0.1 s内完成，辨识速度快且辨识精度高，基本满足应用要求。

4 结束语

本文基于EMA数字化控制设计带一拍延时补偿的无差拍电流预测控制器，考虑实际应用中逆变器的非线性和电机参数失配问题，分别采用平均电压补偿法和RLS参数辨识算法确保控制器性能的准确性和稳定性。仿真结果表明，基于该控制器的EMA系统相比于基于PI控制和PI前馈解耦控制的系统，有着更好的动态响应性能和更高的稳态精度。