非牛顿流体充填料浆的管输摩擦阻力预测

杨晓炳，肖柏林，高谦

（北京科技大学土木与资源工程学院，北京 100083）

胶结充填采矿方法是地下矿山传统三大采矿方法之一，其利用胶凝材料、水和骨料在地表搅拌站搅拌均匀后，形成固体质量分数约60%～80%均匀料浆，利用重力自流或泵送，经管道输送到井下采场空区，经过一段时间的硬化后形成固态胶结充填体，提供支护功能，防止塌陷[1].胶结充填采矿法能有效解决选矿尾砂的地表堆存问题，保护环境，形成绿色循环经济[2]；胶结充填采矿法具有最高的资源回收率，可有效管理地压，提高井下作业安全性[3]；特别是当前浅地表资源的耗竭，采矿活动逐渐往深部发展，例如我国有越来越多的矿山开采达到并超过1 000 m[4-6]，深部开采意味着高温高应力，伴随着岩爆风险，此时胶结充填采矿法以其良好的地压管理能力，将成为深部开采的最主要采矿方法之一.

充填料浆可当作流态混凝土，必须能够实现自流平，也有人称之为低强度混凝土[7].研究如何将充填料浆安全、高效地输送到井下采场空区，是该技术成功应用的关键之一.在工程实际中，充填料浆在管道输送中的沿程摩擦阻力计算，直接影响甚至决定了能否自流输送、充填系统的建设、设备（尤其是泵）选型、管网敷设形式等诸多核心问题.国内外众多学者对摩擦阻力计算进行深入研究，如唐艳蓓等人[8]采用CFX 软件进行数值模拟，分析流体在管道中的沿程阻力系数与管道内壁相对粗糙度的关系；于跃等人[9]以新阳煤矿为背景，提出了适用于该矿的高浓度胶结充填料浆的沿程阻力损失的理论公式；王石等人[10]研究了添加阴离子型聚丙烯酰胺（APAM）前后，全尾似膏体浆料管道输送的沿程阻力计算公式；吴爱祥等人[11]根据流体力学理论建立了考虑管壁滑移效应的膏体管道输送阻力模型，并根据响应面分析确定管道摩擦阻力的影响顺序由大到小依次为灰砂比、尾废比、浓度.国内研究多直接提出用于针对特定某个矿山的阻力计算的经验公式，著名的沿程阻力计算公式还有如金川公式、长沙矿冶院研究公式、鞍山黑色金属矿山设计院公式[12]，然而这些公式应用复杂，往往是经验公式且仅适用于某一特定情况，很少对前提进行界定，缺乏通用性总结；而国外研究多采用无量纲的摩擦阻力系数的概念，并通过Darcy-Weisbach 方程转化为具体沿程阻力值[13].

在国内矿山实际中，也有很多采用设计环管实验的方法，直接对阻力进行准确测量[14-15].环管实验是最准确的测试方法，但其代价极其昂贵，实验过程及操作繁杂费事[16]，在实际中经常需要对料浆进行不断调整，采用环管实验是极其浪费的一种做法.最有效的办法是采用阻力计算公式进行预测，然而在国内众多文献中，并没有多少正确利用阻力系数预测充填料浆阻力的案例.其原因之一是公式的数量繁多，另一个是缺乏考虑料浆流态、状态的多变性，从而选择正确、适用所需情况下的阻力计算方法.因此本文在总结国内外常用关键的一些宾汉塑性体的摩擦阻力系数计算方法的基础上，解释说明各方法的适用条件，然后结合一个具体案例，探讨如何正确应用这些公式进行充填料浆摩擦阻力预测，并对这些公式的适用性进行评价.希望能为正确使用这些模型提供参考.

1 宾汉塑性体的摩擦阻力系数计算模型

在工程实际中，现代充填料浆基本可分为高浓度及膏体两种，表现为非牛顿体特性，且绝大多数是宾汉塑性流体[17].宾汉塑性体料浆同其他流体类似，在管道中流动同样可以分为层流运动、紊流运动及过渡区三种流态，对于过渡区，有太多不确定性，仍是当前的学术难题，因此本节首先按流态分，总结了适用于层流区、紊流区及层流紊流通用的摩擦阻力系数计算方法.

1.1 适用层流区的摩擦阻力系数模型

1.1.1 Buckingham-Reiner 方程

Buckingham-Reiner 方程[18]适用于宾汉塑性体层流状态下的摩擦阻力系数计算模型，如式（1）所示.可见该方程为fL的四阶隐式方程，虽然可以获得精确解析解，但其计算过程复杂，有诸多研究者寻找该方程的显式近似解.

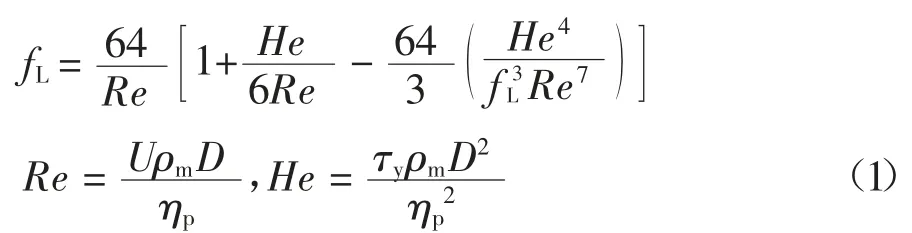
式中：fL为层流中的摩擦阻力系数；D 为管道直径，m；U 为料浆在管道中的平均流速，m/s；ρm为料浆密度，kg/m3；ηp为动力黏度，Pa·s；τy为屈服剪切应力，Pa；Re 为雷诺数；He 为赫德数.

1.1.2 Darby-Melson 模型

Darby-Melson 模型[19]通过修改Buckingham-Reiner 方程中的雷诺数，提出了Finning 摩擦阻力系数Cf：

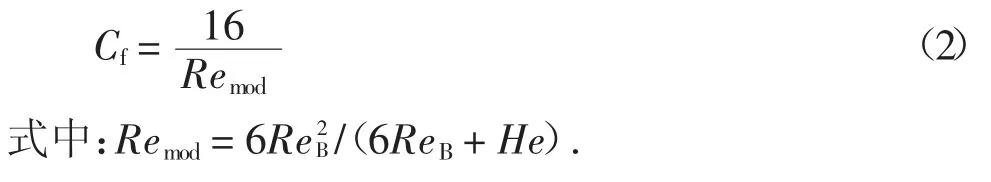
同时他们还提出一个适用于紊流的显式经验方程，如式（3）所示.

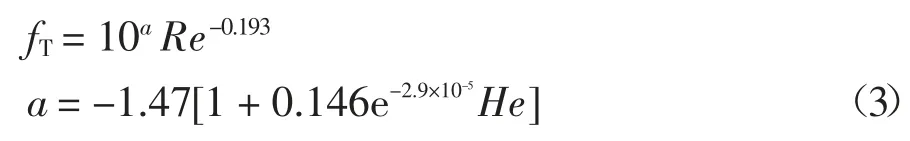
为了得到一个统一同时适用层流和紊流的显式方程，他们提出了式（4）：

式中：m=1.7+40 000/Re；f 为Darcy-Weisbach 摩擦阻力系数；Remod为修正雷诺数；fT为紊流中的摩擦阻力系数.

1.1.3 Swamee-Aggarwal 方程

Swamee-Aggarwal 方程[20]用来直接求解宾汉塑性体层流下的Darcy-Weisbach 摩擦阻力系数fL，它是Buckingham-Reiner 隐式方程的一种近似，如式（5）所示.

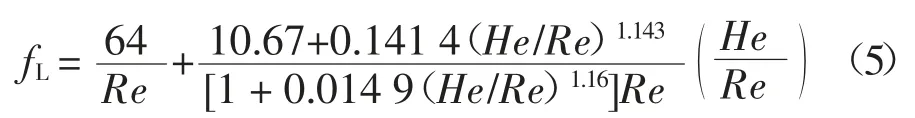
1.2 适用紊流区的摩擦阻力系数模型

1.2.1 Colebrook-White 方程

该模型[21]是一个仅适用于紊流区的通用模型，除了宾汉塑性体，也可用于其他如H-B 等流体，该模型认为，假如相对粗糙度的影响甚微，可用式（6）的隐式方程求解水力光滑管的摩擦阻力系数.

该模型还有一个显式的近似方程来估算水力光滑管的摩擦阻力系数，如式（7）所示.

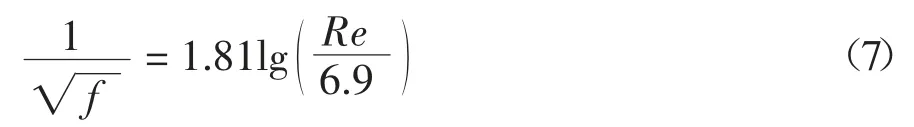
该方程在4 000≤Re≤108 的范围内有效.

1.2.2 Wilson-Thomas 模型

该模型[22]适用于宾汉塑性体料浆的紊流运动阻力系数计算：

1.2.3 Dodge-Metzner 模型

该模型[23]修正了剪切变稀的紊流运动非牛顿体在水力光滑管的摩擦阻力系数：

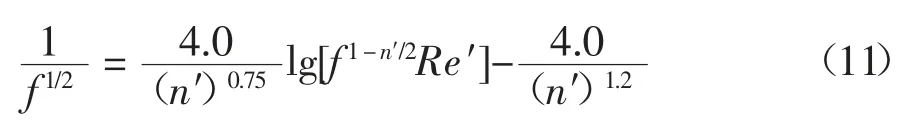
式中：n′为流变指数.

1.3 适用层流紊流的通用模型

Danish 等人[24]通过采用阿多米安分解法提出了计算层流下的摩擦阻力系数计算方法，如式（12）所示.

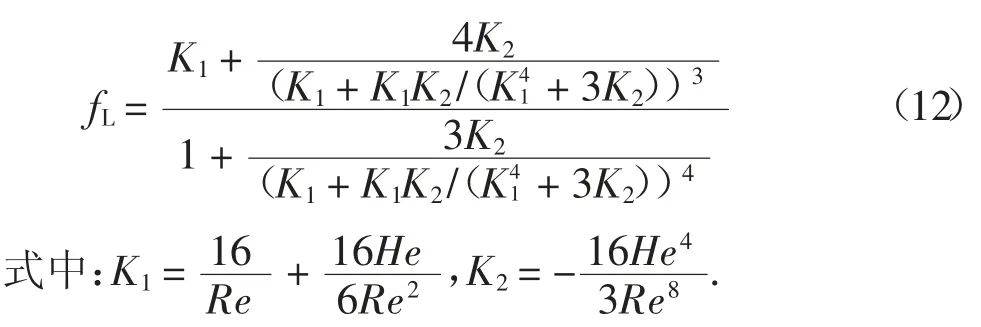
对于紊流，采用式（13）：

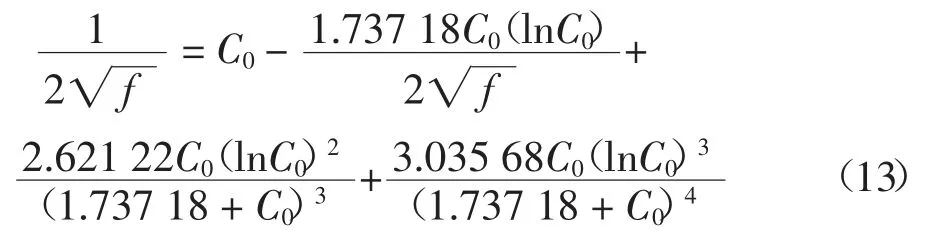
式中：C0=4lgRe-0.4.

2 充填料浆沿程阻力预测的工程案例应用及评价

前面总结了7 种常用的摩擦阻力系数模型，下面结合一个具体案例讨论这些模型的应用，并进行评价.

2.1 利用模型预测沿程阻力的步骤

上述模型中有的适用于层流运动，有的适用于紊流运动，在具体实际应用时必须事先判断充填料浆在管道中的流态，即计算其雷诺数.从式（1）中雷诺数的定义可知，工程中某一流体的雷诺数与料浆的动力黏度、料浆密度、料浆流速以及管道直径有关；密度、流速及管道直径可以根据具体矿山实际情况获取，动力黏度是料浆流变参数之一，需要通过流变仪进行测量.通过流变仪还可以测量另一个流变参数——屈服应力，这两个流变参数也是计算赫德数的必要条件之一.

利用摩擦阻力系数模型预测充填料浆的沿程阻力损失的步骤是：1）用流变仪测量料浆的动力黏度及屈服应力；2）得到的料浆流变参数结合工程实际的管道大小、料浆密度及流速，计算得到料浆雷诺数及赫德数；3）根据得到的雷诺数判断料浆在管道中的流态，结合赫德数，正确选取一个摩擦阻力系数模型；4）根据模型计算对应的摩擦阻力系数，通过Darcy-Weisbach 方程转换成沿程水头损失hf，如式（14）所示.

式中：L 为管道长度，m；g 为重力加速度，m/s2；hf为沿程水头损失，m.

可以将式（14）转化为工程中更为常用的沿程阻力损失S，Pa/m（或kPa/km），如式（15）所示.

2.2 应用案例

2.2.1 工程背景

金川镍矿位于中国甘肃省，是中国最大的镍钴生产基地.龙首矿是金川三个矿山之一，其采用下向进路式分层充填，高浓度料浆通过自流管输到采场，充填倍线3～4，采用水泥为胶结剂，添加量为280～310 kg/m3，骨料为棒磨砂和废石混合骨料（最大粒径5 mm，D50=1～2 mm，棒磨砂废石比例为7 ∶3），料浆质量分数为78%.工程中遇到的问题是，料浆分层离析较严重，对管道磨损及井下充填体稳定性影响很大，其主要原因是缺少-20 μm 细颗粒含量，通过实验对料浆进行优化后，最终优化后的料浆配比是：水泥掺量300 kg/m3，料浆质量分数为78%，采用石灰石粉替换部分原混合骨料，以增加细颗粒含量，替换量为骨料质量的10%.

2.2.2 实验材料

该案例中所用的材料均为龙首矿充填系统实际生产中所用的材料，其中水泥为当地金昌金泥集团的42.5 水泥，骨料为棒磨砂（A1）、废石（A2）混合骨料，添加的细骨料为石灰石粉（A3），这些骨料的粒径级配分布如图1 所示.骨料的主要化学成分如表1所示.

图1 案例中所用的骨料粒径级配分布曲线Fig.1 Particle size distributions of the aggregates in this case

表1 骨料的主要化学成分（质量分数）Tab.1 Chemical composition of the aggregates（mass fraction） %

2.2.3 调整后的料浆流变特性测试

按照上述步骤，首先对调整后的料浆在实验室内进行流变测试，料浆配比为水泥掺量300 kg/m3，固体质量分数为78%，骨料中混合骨料与石灰石粉的比例为9 ∶1，混合骨料中棒磨砂与废石的比例为7 ∶3，料浆密度ρm=2 007.2 kg/m3.

采用Brookfiled 的R/S-SST 流变仪+Rheo3000软件对料浆在室温环境下进行流变测试.测试前将混合物用搅拌机搅拌5 min 至均匀状态，然后装入600 mL 的玻璃烧杯中，立即开始流变测试，流变仪采用VT-40-20 叶片转子，测试时采用控制剪切速率模式（CSR），为了减少通道效应及蠕变效应，测试时先用120 s-1的速率剪切2 min，然后设置剪切速率从120 s-1在120 s 内逐渐降低至0 s-1得到，该期间记录的剪切速率与剪切应力关系如图2 所示，并用宾汉塑性体模型进行拟合，得到的结果为：

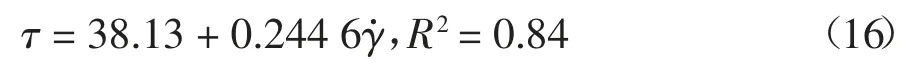
即得到料浆的屈服应力τy=38.13 Pa，动力黏度ηp=0.244 6 Pa·s.

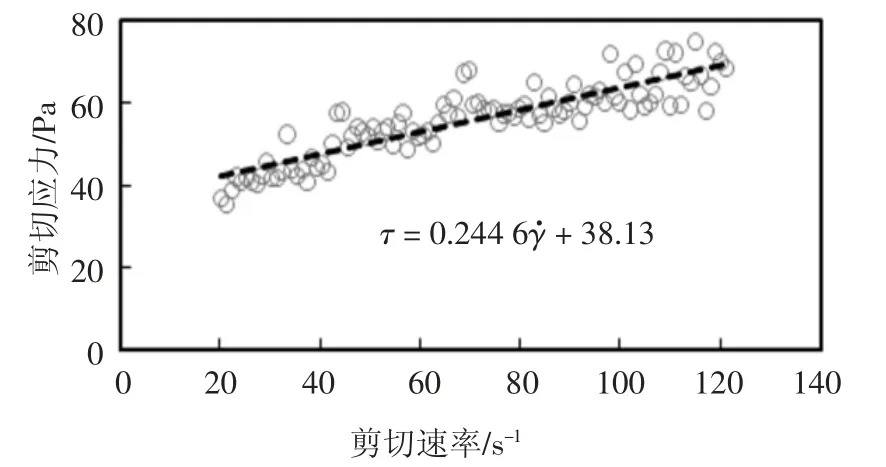
图2 充填料浆流变参数（屈服应力和动力黏度）测试结果Fig.2 Measured results of the rheological properties（yield stress and dynamic viscosity）of the backfilling slurry

2.2.4 计算雷诺数选择合适的模型

龙首矿西部充填站的充填管道直径D=0.11 m，调整后料浆的密度ρm=2 007.2 kg/m3，西部充填站运行中控制系统终端监测得到的流量除以管道截面积可以换算成料浆流动速度（见图3）；把已知参数代入式（1）雷诺数的计算公式，可以得到雷诺数的变动范围，如图3 所示.

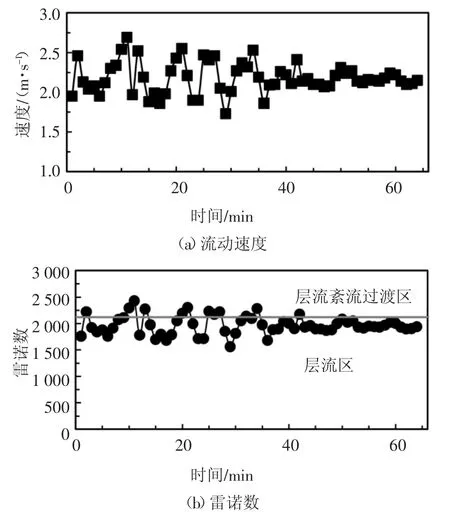
图3 充填系统中料浆的流动速度及雷诺数变化Fig.3 Variation of velocity and Reynold Number in the backfill system

由图3 可知，该条件下料浆在管道中大部分时间处于层流运动（雷诺数小于2 100），但也有一小部分由流速变化导致其处于层流紊流过渡区.引起料浆流速变化波动的原因有3 个：1）充填系统配比波动，如料浆质量分数为78%，但实际中不可能完全稳定在78%，一般在77%～79%间波动，这是充填系统本身特性所决定，是不可避免的；2）充填材料，尤其是骨料的差异性，搅拌桶中虽然是连续搅拌，但在不同时刻放入的骨料具有差异性，其粒径级配不可能完全一样，这将引起料浆密度、黏度、屈服应力等各个特性的波动，从而造成流速波动；3）充填料浆的非均质性，高浓度料浆可以当作似均质流，但达不到理想均质状态，因此料浆在管道纵截面上的速度会有细微差异，再加上金川充填料浆中骨料颗粒的最大粒径达12 mm，料浆中大颗粒的不规则运动恰好经过管道传感器位置将可能引起波动异常.

因此，可以把该料浆当作是层流运动，根据第1节所总结的模型，该情况下可选用的模型有Buckingham-Reiner 方程、Darby-Melson 模型、Swamee-Aggarwal 方程和Danish-Kumar 模型；其中Swamee-Aggarwal 方程只是Buckingham-Reiner 高阶隐式方程的显式近似求解，因此两个方程的解差异不大，为了简化计算，采用Swamee-Aggarwal 方程，即最终采用式（4）、式（5）和式（12）3 种模型进行预测.

3 结果验证与评价

3.1 验证实验

为了验证及评价所选方法所预测沿程阻力损失的准确性和适用性，在龙首矿西部充填站已有的充填管道系统架设压力传感器，通过实际工业实验验证模型的适用性与准确性.西部充填站的充填管网水平管总长为1 520 m；垂直管总长为421 m，充填倍线3.61，管道内径110 mm；共安装了4 个压力变送器以监测料浆在管道流动中的阻力变化，并采用无纸记录仪每隔1 min 记录一次监测点的压力.管网简图、监测点的位置及安装如图4 所示.

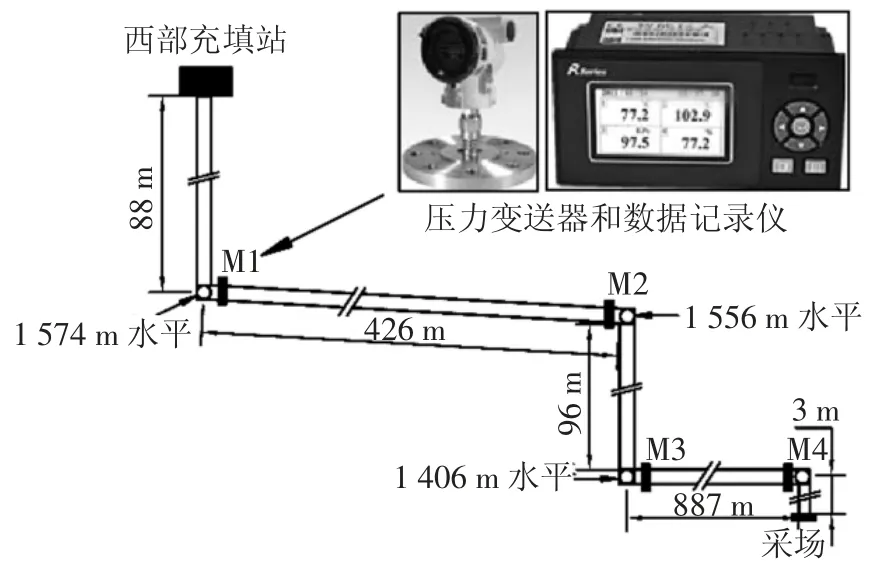
图4 西部充填站管道布置及压力变送器安装示意图Fig.4 Schematic of the pipeline system and the installation of pressure transmitter in the West Backfill Plant

3.2 结果分析与评价

以调整后的料浆配比进行工业实验，所有流量流速、压力、浓度等监测信息都传输至地表控制终端，根据监测点的流速等相关数据代入模型，可以计算得到各模型的预测摩擦阻力系数，再经过式（15）即可转换成对应预测的沿程阻力损失；实际监测中将两个不同监测站监测的压力差除以该两个监测站的距离即为实际监测沿程阻力损失；最终采用的3种模型沿程阻力预测结果与监测点所记录的实际阻力损失对比如图5 所示.从图5 中可以得到：

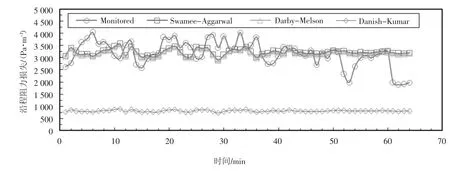
图5 预测的沿程阻力损失与实测损失对比Fig.5 Comparison on pressure loss unit per length between measured and predicted

1）首先对于实际监测得到的压力损失，其波动较大，原因除了在2.2.4 所述的配比波动、骨料变异性及料浆非均匀性以外，还与实际系统运行状态和充填采场倍线大小等关系密切相关，在工业中这种波动是正常及不可避免的.

2）Swamee-Aggarwal 方法及Darby-Melson 方法预测得到的沿程阻力几乎重合，前者略大于后者，这是因为这两个方程的本质都是Buckingham-Reiner，只是进行显式求解的不同造成了略微不同.但两者预测到的沿程阻力与实际监测的沿程阻力基本一致，处于同一水平波动，吻合良好；而与实际监测差异较大的部分点是由于流态变化造成的.由前文所述速度及雷诺数波动中，已经验证有极少时刻，料浆处于层流紊流过渡区，此时沿程阻力将十分不可控，变化较大，而这里的这两种方法都是适用层流运动下的阻力计算，因此造成这些部分预测值与实测值差异较大.从工程实际上看，Swamee-Aggarwal 方法及Darby-Melson 模型能预测得到与实际工业充填中相吻合的阻力损失.

3）Danish-Kumar 模型预测得到的沿程阻力损失与实际相差较大，其预测值远小于实测值，且对速度波动的反应也不明显，“失真”较严重.在计算过程中发现中间参数K2十分微小，达到10-10，本文认为其比较适用赫德数He 较大的流体（50 000 以上），但考虑篇幅问题并未进行深入解释.

4 结论

本文通过总结文献常用的7 个非牛顿流体的摩擦阻力系数计算模型，按照其适用流态类型进行分类并简要介绍讨论了具体用法，然后结合一个具体案例论述了模型的具体应用，得到了以下几点结论：

1）高浓度或膏体充填料浆可以看作均质或似均质的非牛顿体，可以通过选择正确的模型计算其在工程实际管道流动中的沿程阻力损失；正确模型的选择十分重要，必须先考虑工程实际流体的类型（幂次、宾汉体、H-B 体）、流态（雷诺数），才能根据这些前提选择准确的阻力系数模型.

2）对于宾汉塑性体的层流运动，Buckingham-Reiner 方程、Darby-Melson 模型、Swamee-Aggarwal方程和Danish-Kumar 模型是4 种最常用的预测模型，其中Buckingham-Reiner 方法是4 次隐式方程，必须通过迭代才能求解，实际中往往用Darby-Melson 模型和Swamee-Aggarwal 方程进行近似替代；通过实验验证，Darby-Melson 和Swamee-Aggarwal 方法所预测的沿程阻力与实际监测十分吻合，处于同一平均位置波动，是宾汉塑性体层流运动首选的阻力预测模型，而Danish-Kumar 模型则过低估计阻力值，适合赫德数较大的流体.

3）实际中速度、沿程阻力波动的原因与料浆配比波动、骨料变异性、料浆非均匀性、实际系统运行状态和充填采场倍线大小等因素密切相关，是不可避免的；尽管如此，Darby-Melson 和Swamee-Aggarwal 方法也能根据速度波动模拟其阻力的变化，而当料浆进入层流紊流过渡区时则误差较大，对于大部分时刻处于过渡区或紊流区的流体必须采用其他模型进行预测.