基于ASCP-CS 算法的桥式吊车滑模控制器设计
2020-06-30王天雷谭南林张人丰邱炯智KennethTeoTzeKin
王天雷,谭南林,张人丰,邱炯智,Kenneth Teo Tze Kin
(1.北京交通大学 机械与电子控制工程学院,北京 100044;2.五邑大学 智能制造学部,广东 江门 529020;3.沙巴大学 工程学院,沙巴 哥打基纳巴卢,马来西亚)
桥式吊车系统常用于各类重工业场地以及港口货物运输,工作时依靠台车悬挂的吊绳将负载牵引到指定位置.由于桥式吊车控制量维度少于其自由度,在运行过程中需要台车精准定位以及抑制负载摆动,致使控制难度大为增加.为解决上述问题,使桥式吊车系统高效稳定运行,学者们做了大量研究[1-8].
吊车控制方式可分为开环和闭环控制,开环控制包括轨迹规划[3]、输入整形[4]等;闭环控制包括最优控制[5]、模糊控制[6]及滑模控制[7-8]等.滑模控制由于具有快速响应、设计简单、鲁棒性强等特点,广泛应用于欠驱动系统的控制中[9],但滑模控制器的参数整定过程复杂,整定结果对控制效果影响较大.因此,学者们对基于参数整定的滑模控制进行了研究[10-14].
在滑模的优化控制方法中,陈志梅等[10]提出了基于粒子群优化(Particle Swarm Optimization,PSO)的滑模控制方案,实现了对倒立摆状态轨迹的跟踪控制.Vishnu 等[11]采用改进粒子群对Buck 电路的滑模控制进行优化,降低了Buck 电路的超调,提高了电路的鲁棒性.马群[12]通过把变论域自适应的模糊滑模控制与粒子群算法结合,提高了负载的定位速度以及降低了摆角的角度.罗俊尧等[13]采用遗传算法(Genetic Algorithm,GA)对起重机的滑模控制器参数进行优化.Soufi 等[14]提出了一种基于粒子群优化的滑模控制策略,并将其应用于风力发电并网系统中,实现了最大限度利用风能,并能同时限制电磁转矩的变化.但GA 存在调节参数较多且设置难度较大的局限,而参数相对较少的PSO 算法则容易陷入早熟.
Yang 和Deb[15]提出的布谷鸟搜索(Cuckoo Search,CS)算法具有易实现、可调参数少、全局搜索能力好等特点,但也存在后期收敛精度不高、收敛速度缓慢等问题.为此,郑洪清等[16]利用每次迭代的结果来动态更新移动步长的方式替换Lévy 飞行机制,避免了游走的随机性;彭建新等[17]根据适应度值的分配进行步长和发现概率的自适应改变,提高了收敛速度与寻优精度.在控制系统应用中,Stojanovic 等[18]采用CS 算法对并联机器人控制器的参数设置进行优化控制,对比粒子群与遗传算法,CS 算法具有更好的优化性能.朱笑花等[19]通过借鉴核糖核酸(Ribonucleic Acid,RNA)的茎环结构对布谷鸟搜索算法进行改进,并用于吊车PID 控制器的参数整定优化,提高了吊车系统的消摆与定位效果.
综上,为提高算法的全局寻优能力和后期的搜索精度,本文提出一种改进的CS 算法,即在算法中自适应选取染色体交差操作点以及选用改进的自适应步长函数.并采用该算法设计了桥式吊车滑模控制器,通过与布谷鸟滑模控制器(CS Sliding Mode Controller,CS-SMC) 以及粒子群滑模控制器(PSO Sliding Mode Controller,PSO-SMC)的控制效果进行测试比较,结果表明本文设计的控制器性能良好.
1 桥式吊车系统的物理模型
图1 为桥式吊车系统的物理模型,模型中负载通过吊绳悬挂在台车上,在力F 作用下台车通过吊绳牵引将负载运送到指定位置.
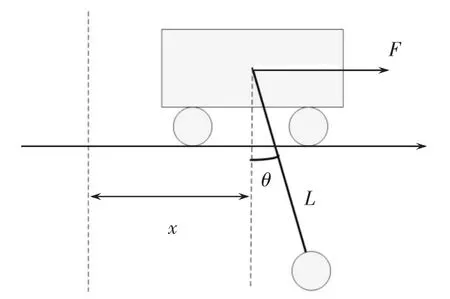
图1 桥式吊车物理模型Fig.1 Physical model of bridge crane
采用拉格朗日方程对吊车进行建模,忽略各类摩擦力、负载的空气阻力以及绳子的弹性形变.拉格朗日方程普遍形式如下:
式中:T 为系统动能;P 为系统势能;qi为状态变量(x,θ);Qi为非保守广义力.该系统的动能T 表示为:
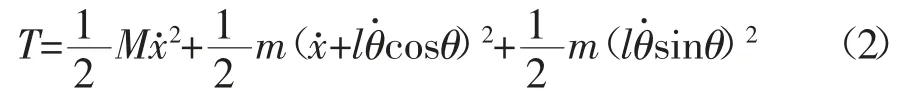
式中:m 为负载质量;M 为台车质量;x 为台车位置;l为吊绳长度;θ 为负载摆角.

式中:g 为重力加速度.联立式(1)~式(3),可得如式(4)所示的动力学模型:
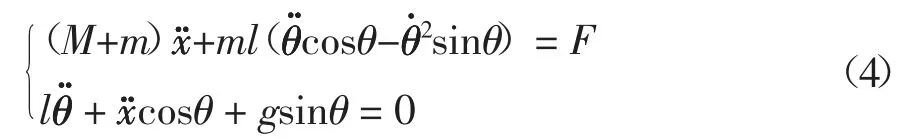
式中:F 为水平方向的控制力.
定义桥式吊车的系统状态变量为XT=[x1,x2,x3,,输入u 为u=F,输出为Y,x1和x2分别为台车位置和速度,x3和x4分别为负载摆角和加速度,则系统动力学模型的状态方程可化为:

其中,非线性函数f1、g1、f2、g2分别定义如下:
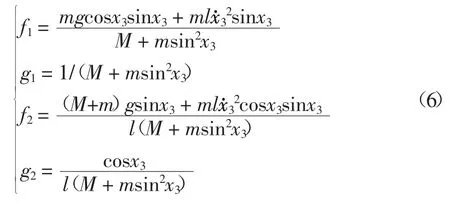
2 桥式吊车系统的滑模控制
由式(4)可知,吊车系统输入控制力F 需完成精准的台车位置控制与良好的负载摆角抑制效果,故滑模面设计如式(7)所示:

式中:xd为台车位移的目标值,与位置误差权重a、角度误差权重b 均为常数.选取指数趋近律控制:
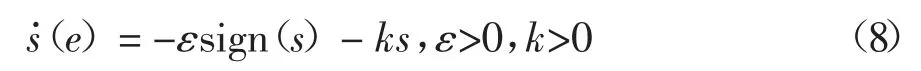
式中:ε 为切换增益,k 为指数系数,均为大于0 的常数;sign(s)是符号函数.为削弱控制器抖振问题,采用sat(s)函数替换式(8)中的sign(s)函数.sat(s)可定义为:
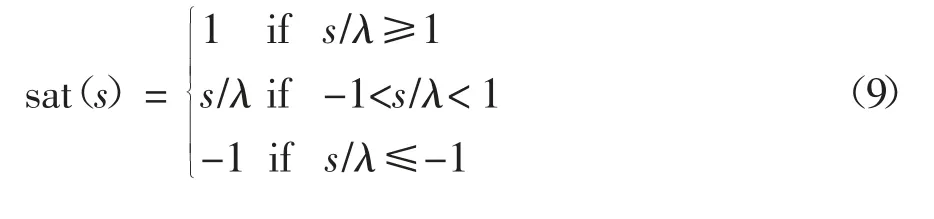
式中:λ 为常数.对式(7)进行求导可得:

联立式(7)和式(10)可得:

联立式(4)~式(11)可得系统控制器输出u 为:
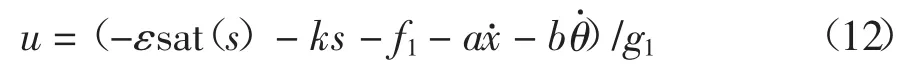
3 ASCP-CS 算法
Lévy 飞行机制与偏好随机游走机制在一定程度上缓解了CS 算法搜索精度不足的缺陷,然而桥式吊车控制器较为复杂的优化问题需要优化算法具备更强的搜索能力.朱笑花和陶吉利等[19-20]的研究表明,RNA 分子的变异以及交叉操作能够使CS 算法和遗传算法的搜索效果更好.受其启发,本文设计了自适应选取交叉点的算子,增加交叉操作的合理性,并引入新步长的自适应改进策略,提出一种具有自适应选取交叉点的布谷鸟搜索算法(Cuckoo Search Algorithm with Adaptively Selecting Crossover Points,ASCP-CS).
3.1 CS 算法
CS 算法的规律可概括为:1)每个布谷鸟随机选择一个宿主鸟巢生蛋;2)保留适应度较好的鸟巢进入下一代;3)宿主发现寄生的鸟巢并丢弃的概率为Pa,然后选择新的位置筑巢.其中下一代鸟巢位置更新采用Lévy 随机游走方式,该方式具有“长期短距离游走结合偶尔的长距离跳跃”特点,可保证算法的全局搜索能力.鸟巢位置更新方法如式(13)所示.


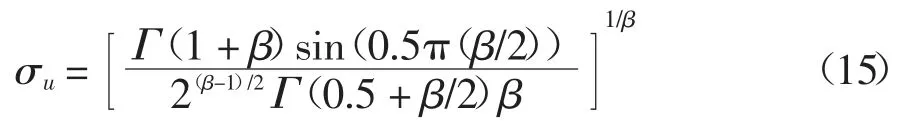
式中:Γ 是标准的Gamma 函数;本文取β 为1.5.
宿主以Pa的概率丢弃部分解后,会通过偏好随机游走的方式产生新的解,如式(16)所示:

3.2 自适应步长
为增强CS 算法的搜索能力,前期搜索范围较大,后期需缩小搜索范围以获得更高的搜索精度.针对上述问题,对算法中的步长α 进行如下改进:

式中:α1为初始时刻步长;b1为步长变化范围;g1为步长变化最大时的进化代数;g 为当前进化代数.
3.3 交叉操作算子
参考遗传算法的基本思想,即通过交叉操作达到增加个体多样性,本文在CS 算法的搜索过程中引入交叉操作的算子,如图2(a)所示.由于在交叉的过程中个体发生变异的情况充满随机性,可能会导致算法的收敛速度变慢.改进的CS 算法在交叉操作中设计一种新型自适应选取交叉点的交叉操作算子,利用该算子,在搜索前期交叉操作的选取集中在序列的高位区域,增加算法的搜索空间;而搜索后期集中在序列的低位区域,能增加搜索精度.具体操作如图2 所示.
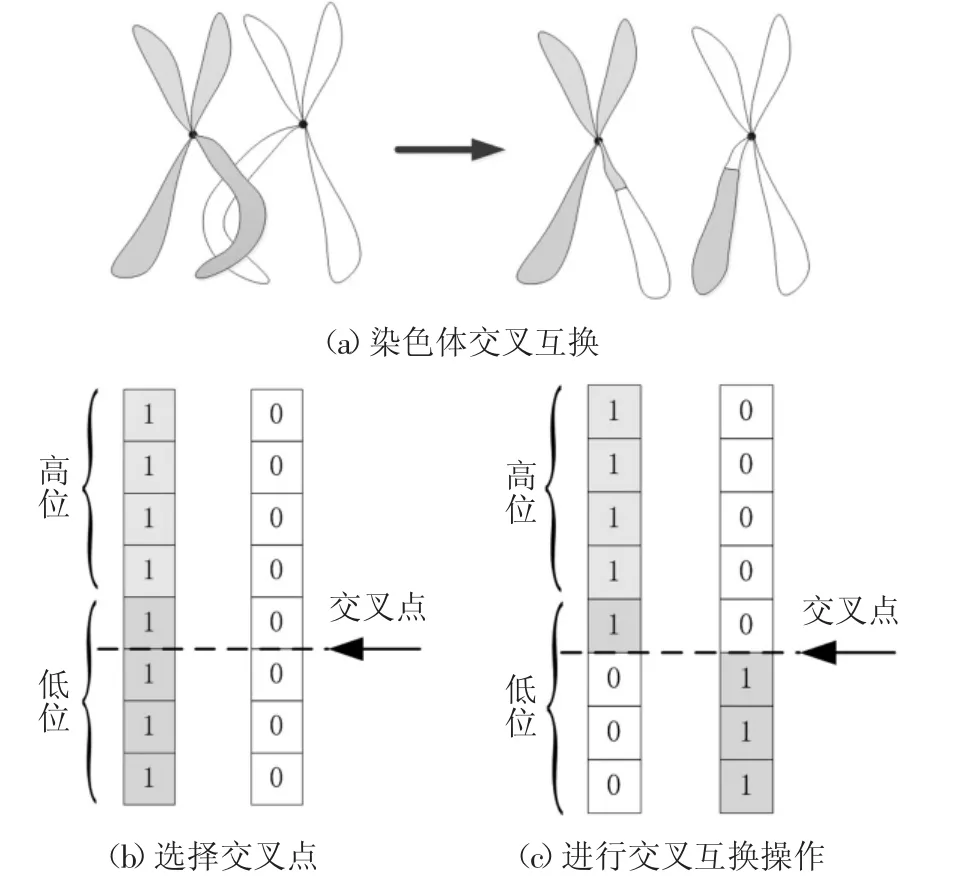
图2 染色体交叉互换操作示意图Fig.2 Diagram of chromosome crossing operation
自适应选取交叉点的概率公式为:

式中:b2为概率变化范围;g 为当前进化代数;c1和g0分别为步长变化时候速率和对应的进化代数.在选择序列的交叉操作点时,随机产生一个概率Pn,当Pn<P0时,在序列的L/2 处到L 处的高位区域选择交叉点,反之则在低位区域进行选取.
3.4 ASCP-CS 算法的步骤
ASCP-CS 算法流程如图3 所示.1)初始化算法相关参数;2)通过式(18)的步长公式更新鸟巢位置,并计算适应度值;3)通过贪婪算法保存适应度值最优的鸟巢;4)为每一个鸟巢随机选取一个概率Pt,当Pt<Pa时则丢弃原来的鸟巢,并通过公式(17)的偏好随机游走方式更新鸟巢的位置;5)通过贪婪算法保存适应度值最优的鸟巢;6)在较好的解中随机选取n/2 个鸟巢进行两两配对,让每个解在交叉点进行交叉操作;7)通过贪婪算法保存适应度值最优的鸟巢;8)判断是否满足算法的停止条件;9)不满足时重新第2 个步骤;10)满足即停止搜索,输出最优的鸟巢.

图3 改进布谷鸟搜索算法流程图Fig.3 Improved cuckoo search algorithm flow chart
4 数值寻优与结果
为检验ASCP-CS 算法的性能,分析自适应选取交叉点策略和变步长对该算法收敛速度和全局搜索能力的影响,本文选取了CS 算法、PSO 算法与ASCP-CS 算法进行对比.4 个测试函数全局最小值均为0,用于考察收敛速度的单峰函数f1,以及考察收敛速度和全局搜索能力的多峰函数f2、f3和f4.4 个函数定义如下:
1)Sphere 函数.
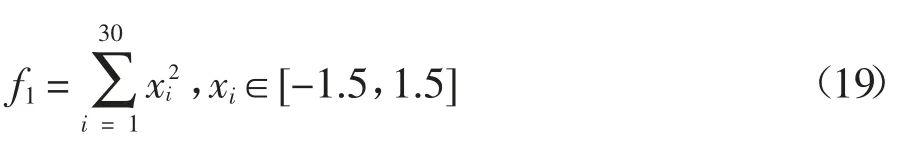
2)Rastrigin 函数.
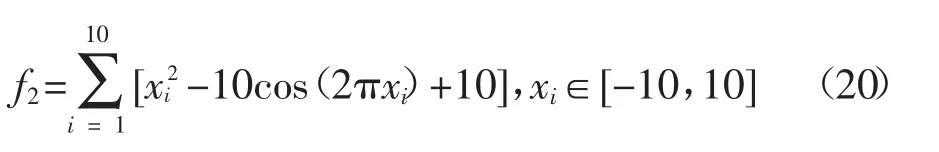
3)Schaffer 函数.

4)Ackley 函数.
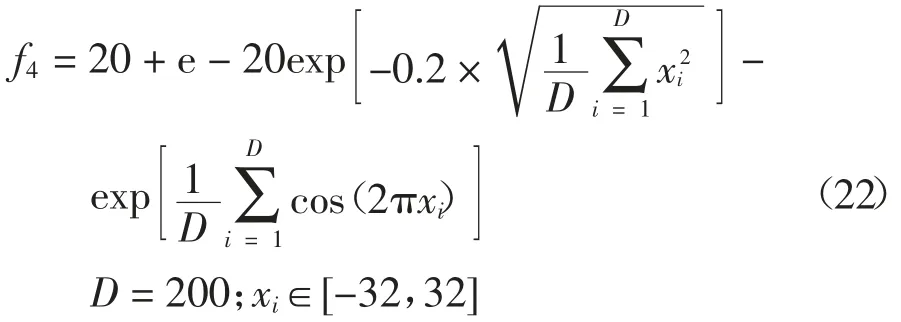
初始化搜索算法的参数时,为保持条件一致,ASCP-CS 算法与CS 算法的鸟巢数目n=15,最大迭代次数gmax=200,二进制序列长度L=log2max(|xmin|,|xmax|),步长参数a1=0.9,b1=0.7,交叉点的自适应变异概率b2=1,c1=20/gmax,g0=gmax/2,被发现概率Pa为0.25.PSO 算法的参数设置如下:种群规模n=15,惯性权重w=0.7,学习因子c1=c2=0.7.仿真环境为Windows 10,内 存16 GB,CPU 为Inter i7 系 列,MATLAB 2014b.各算法独立运行100 次,对不同函数的几种算法计算结果如表1 所示.

表1 寻优结果比较Tab.1 Comparison of optimization results
4.1 寻优精度比较
分析表1 数据可知,从f1到f44 个函数的测试当中,ASCP-CS 算法的寻优精度、接近程度以及稳定性明显更高更好.
4.2 搜索能力比较
图4 为4 个测试函数的3 种算法各自运行100次,并取适应度值平均后的对数值绘制的寻优收敛曲线.由图4 可知,在4 个测试函数中,PSO 算法虽收敛速度快,但均容易早熟,CS 算法虽有一直下降的趋势,但明显比ASCP-CS 算法慢;PSO 算法的收敛速度虽快,但最终会陷入到局部解中,ASCP-CS 算法与CS 算法明显具有很强的全局搜索能力.

图4 函数f1~f4 的收敛曲线Fig.4 Converges curve of the function f1~f4
5 滑模控制器参数优化及系统仿真分析
MATLAB/Simulink 环境下,应用ASCP-CS 算法对滑模控制器4 个参数(滑模面参数a、b 及趋近率函数参数ε、k)进行离线优化,其实施过程如图5所示.
1)对桥式吊车控制器模型参数进行初始化;2)利用ASCP-CS 算法优化计算出滑模控制器4 个参数;3)桥式吊车模型运行结束后,利用获得系统状态量(x,θ)及控制力u 计算出目标函数J 的数值;4)ASCP-CS 对目标函数值进行评价,如果到达目标阈值或者满足最大迭代次数则结束算法运行,反之返回步骤2 继续计算.
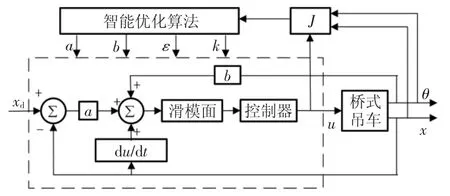
图5 自适应滑模控制结构示意图Fig.5 Schematic diagram of adaptive sliding mode control structure
为保证吊车系统瞬态响应时振荡较小以及系统响应较快,并对控制系统的参数具有较好的选择性,采用控制系统性能评价指标ITAE (Integrated Time and Absolute Error)定义式(23)所示的目标函数J:
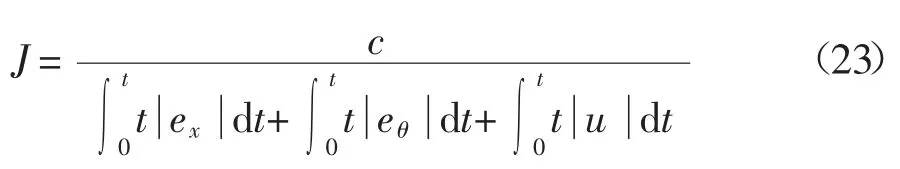
为更加充分说明该智能优化算法在桥式吊车滑模控制器的参数整定方面的效果,将ASCP-CS 算法、CS 算法与PSO 算法优化的滑模控制器进行控制效果的仿真对比实验.采用文献[15]提供的桥式吊车参数:台车质量M=5 kg,负载质量m=1 kg,绳长l=1 m,搜索空间分别为:a、ε、k∈[0,100],b∈[-100,100],目标函数J 的参数c=1 000;3 种算法的迭代次数均设置为G=50,目标函数的阈值设为σ=100,3 种优化算法在同时达到最大迭代次数或者超过该阈值即可认为结束本轮优化.3 种算法的目标函数寻优对比实验结果如图6 所示.

图6 3 种算法的目标函数寻优过程Fig.6 Objective function optimization process of three algorithms
对比图6 的寻优情况,可知ASCP-CS 算法在第16 代时目标函数值已经达到所设置的目标函数阈值σ,即已经收敛,而CS 算法以及PSO 算法依然在逐步收敛中.ASCP-CS 算法的收敛速度明显得到提高.
通过3 种优化算法得到的滑模控制器的参数(切换增益e,指数系数k,位移权重a,角度权重b)见表2.

表2 滑模控制器参数Tab.2 Sliding mode controller parameters
5.1 控制器消摆和定位性能
图7 为基于3 种算法的滑模控制器的位置与摆角曲线.由表2 中适应度值数据表明,ASCP-CS 算法与CS 算法相比,在精度上有明显的提高.由表3、表4 和图8 可知,在ASCP-CS 滑模控制器作用下,负载最大摆角在0.11 rad 以内,在3.9 s 左右收敛到零.同时与CS 算法和PSO 算法优化的滑模控制器相比,ASCP-CS 滑模控制器响应更迅速,震荡更小,控制效果更好.
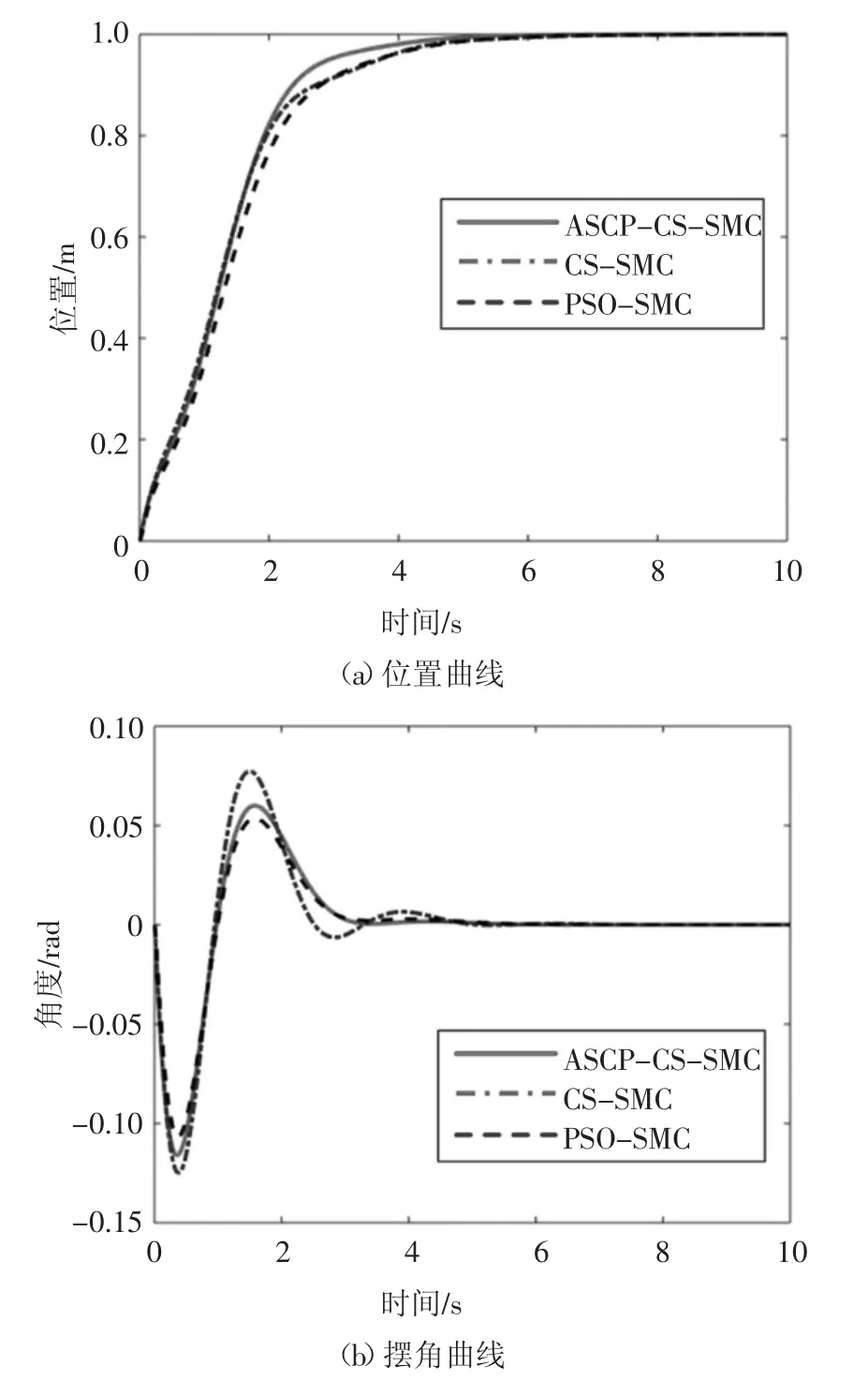
图7 位置与摆角的曲线Fig.7 Curves of position and swing angle
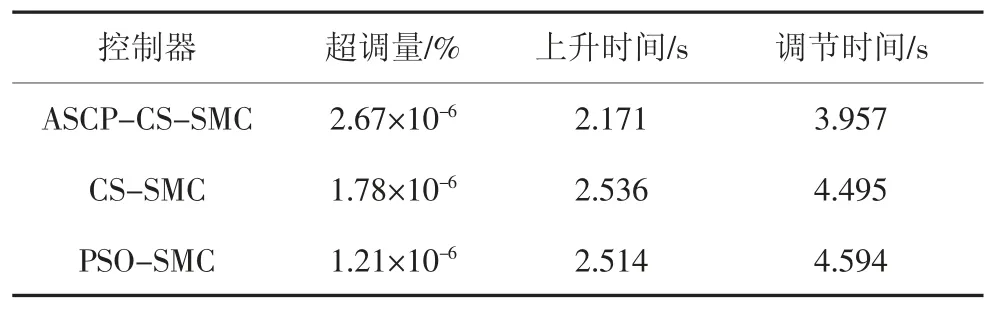
表3 吊车位置性能Tab.3 Trolley position performance
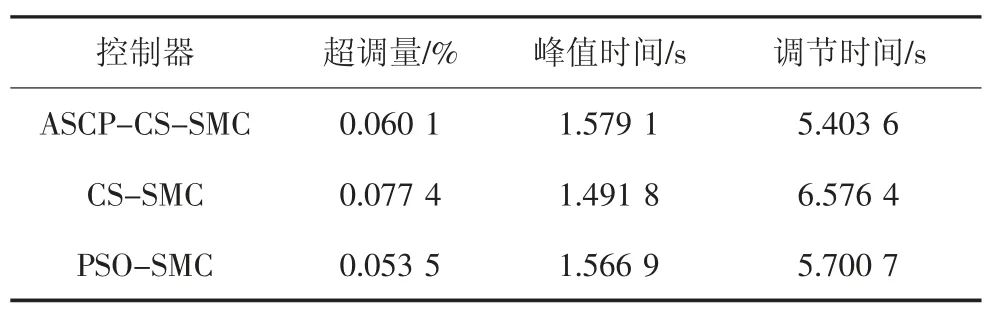
表4 吊车摆角性能Tab.4 Trolley swing angle performance
5.2 控制器鲁棒性实验
5.2.1 实验安排
为验证ASCP-CS 算法优化的桥式吊车滑模控制器的鲁棒性,本文分2 种情况进行仿真测试.
仿真情况1:施加外力的方式.在运行5 s 时,施加一个幅值为10 N 的干扰外力,以测试系统鲁棒性.仿真结果如图8 所示.

图8 外加干扰的曲线Fig.8 Curves with external interference
仿真情况2:改变吊车系统的负载质量m 与绳长l 两个参数.第1 组参数:m=1 kg,l=1 m;第2 组参数:m=1 kg,l=0.75 m;第3 组参数:m=0.5 kg,l=0.75 m;第4 组参数:m=0.5 kg,l=1 m.仿真结果如图9 所示.
5.2.2 实验结果分析
1)抗干扰性分析.由图8 可知,系统受到干扰后,负载位置受影响较小,负载摆角在干扰瞬间会产生一定摆动,经过约2 s 再次稳定,恢复到零摆角,表明ASCP-CS 的滑模控制器具有较好的抗干扰能力.
2)变载荷稳定性分析.由图9 可得:①改变系统质量及绳长,对ASCP-CS 滑模控制器的位置影响较小;②绳长不变,仅改变负载质量,负载的摆角无明显变化;③负载质量不变,仅改变绳长,负载摆角受到一定影响,随着绳长变短,摆角幅值变小.

图9 变参数控制曲线Fig.9 Control curves with variable parameters
综上可得,通过外加干扰以及改变系统参数的仿真实验结果表明,基于ASCP-CS 算法的滑模控制器具有较强的抗干扰能力和鲁棒性,可适应吊车系统在不同的工作状态下稳定地运行.
6 结束语
本文提出一种能够自适应选取染色体交叉操作点的ASCP-CS 算法,该算法能获得较好的全局搜索能力和后期搜索精度,而利用该算法优化的桥吊滑模控制器具有较好的消摆和定位性能,以及良好的鲁棒性.
1)为增强CS 算法的搜索速度和精度,设定自适应搜索步长;同时在搜索过程中交叉操作算子环节,设计一种新型自适应选取交叉点的交叉操作算子,利用该算子能进一步提升搜索性能.
2)通过4 个测试函数与CS、PSO 算法进行寻优测试对比,ASCP-CS 算法全局搜索能力更强,更不容易早熟,同时兼顾较高的搜索精度和较快的收敛速度.
3)将ASCP-CS 算法用于设计桥式吊车滑模控制器,相比于其他两种控制器,该控制器在3.9 s 左右摆角收敛到零且负载最大摆角在0.11 rad 以内,稳态误差较低.而且ASCP-CS 在鲁棒性的仿真测试中具备较高的鲁棒性.
