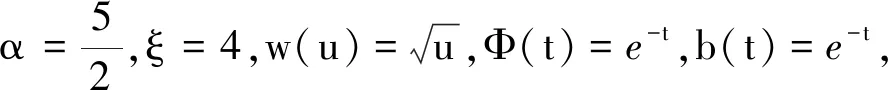一类无穷区间上分数阶微分方程的三点边值问题解的存在性
2020-06-18张瑞鑫王文霞
张瑞鑫,王文霞
(太原师范学院数学系,山西 晋中 030619)
近年来,由于分数阶微分方程在物理、生物、化学等很多领域有着重要的应用,分数阶微积分理论的研究得到了极大的关注.有限区间上的分数阶微分方程的研究已取得很多优秀成果[1-3],但无穷区间上的分数阶微分方程的研究成果相对较少[4-9].
冯子鑫、周宗福和许文序[4]运用压缩映像原理及单调迭代法研究了如下的边值问题:
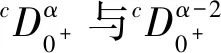
受上述文献的启发,本文研究如下无穷区间上的三点边值问题:
(1)
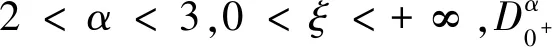
1 预备知识及引理
定义1[2]连续函数f:(0,+∞)→R的α>0阶Riemann-Liouville分数阶积分的定义为
对任意的α>0,右端在R+上逐点可积.
定义2[2]函数f:(0,+∞)→R的α>0阶Riemann-Liouville分数阶积分的定义为
其中,n是大于等于α的最小正整数,等式的右端在(0,+∞)有定义.

其中ci∈R(i=1,2,…,n)为任意常数,n为大于等于α的最小正整数.
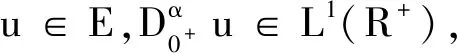
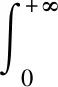
引理2假设(H0)成立,h(t)∈C[0,+∞)∩L[0,+∞),那么边值问题
(2)
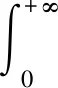
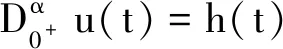
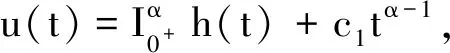
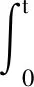
故
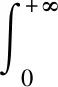
再由
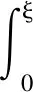
及(2)的边界条件得
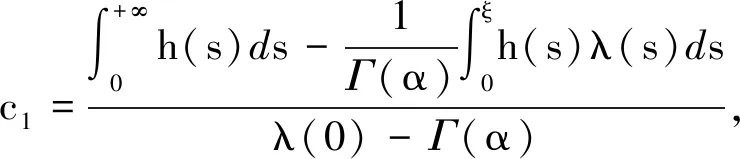
其中λ(0)>Γ(α),因此
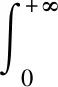
证毕.
引理3函数G(t,s)满足以下性质:
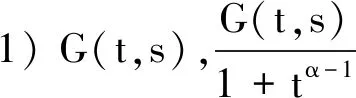
证明由G(t,s)的表达式可知结论1)成立.以下证明结论2).
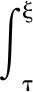
证毕.
注
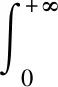
其中,
G1(t,s)=
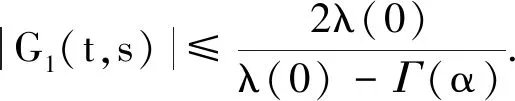
定义空间
其范数分别定义为:
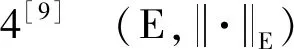
定义算子T如下:
则T:Y→Y,且
引理5[9]设Z⊆Y是一个有界集,若
2)任意给定ε>0,存在常数T=T(ε)>0,使得对任意的t1,t2≥T及u(t)∈Z有
及
均成立,则Z是一个相对紧集.
引理6[10](Schauder不动点定理)设D是E中有界凸闭集(D不一定有内点),A∶D→D全连续,则A在D中必具有不动点.
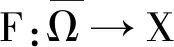
2 主要结果
本文将用到如下假设:
(H1)f∈C(R+×R×R,R),且存在非负函数p,q,r∈L1(R+),tα-1p∈L1(R+),使得
f(t,u,v)| (H2)a∈C(R+,R+),(0 (H3)f∈C(R+×R×R,R),存在w∈C(R+×R+)非减及Φ∈L1[0,+∞)使得 a(t)f(t,(1+tα-1)u,v)|< Φ(t)(w(u|)+w(v|))+ 定理1假设(H0),(H1),(H2)成立,若 λ(0)-Γ(α)≥ 则边值问题(1)至少有一个解. 第一步 证明T:U→U.选取 所以T:U→U. 第二步 证明T:U→U是连续的.设un∈U,n=1,2,3,…,un→u∈U(n→+∞),于是 q(s)]+a(s)r(s)}ds<+∞, a(s)r(s)}ds<+∞. 故 这就证明了TΩ在[0,+∞)上任意有限子空间上是等度连续. 又因 所以对任意的u∈Ω有 因此,T(Ω)在无穷点收敛.由引理5知T(Ω)为U中的列紧集,故T为紧算子. 综上所述,T:U→U是全连续算子.故由引理6可知边值问题(1)在U中至少有一个解.证毕. 定理2假设(H0),(H2),(H3)成立.若(H3)中的函数Φ,w满足∃ρ>0使得 (3) 证明首先证明T是解Y→Y连续的.设un(n=1,2,3,…)是Y中任一序列,并且un→u(n→+∞),于是 即T(I)一致有界.又对∀t1,t2∈R+,不妨设t1>t2,以及任意的u∈I有 由此可知TΩ在[0,+∞)上任意有限子空间上等度连续. 此外又因 及 所以对任意的u∈I有 因此,T(I)在无穷点收敛.由引理5知T(I)为Y中的列紧集,故T为紧算子,又由T的连续性可知T:Y→Y全连续. 进而有 例1考虑下面边值问题 及 显然, 经计算可知 因定理1的条件皆满足,所以边值问题至少存在一个解. 例2考虑下面边值问题 a(t)f(t,u,v)= |a(t)f(t,(1+tα-1)u,v)|≤ 令ρ=5,有 因定理2的条件皆满足,所以该边值问题至少存在一个解.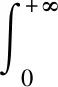
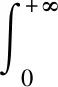
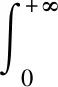
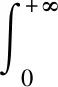


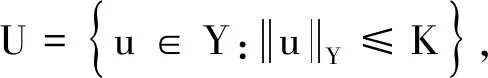
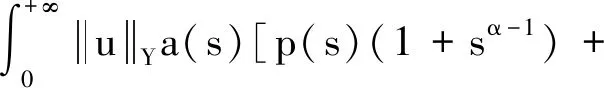
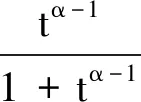
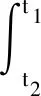
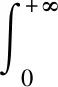
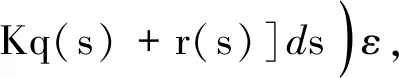
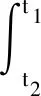
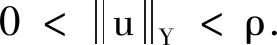

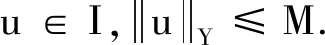

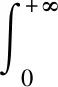
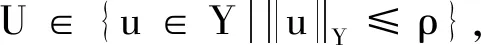

3 例子