基于隐式广义预测控制的风电机组控制方法研究

张家清，施伟锋

(上海海事大学，上海 201306)

0 引 言

目前，由于化石能源的消耗造成的能源需求和环境污染(污染、酸雨、温室效应等)问题日益严重，而无污染的可再生能源是解决该问题的一个非常重要的途径[1-2]，因此受到了广泛的关注。风力发电是目前风能最主要的利用形式，但受风速的波动性、随机性等特点的影响较大。又因为大型风机桨距角的调整具有短时的滞后性，会导致桨叶角度调整不及时，产生过调整、频繁调整等现象，影响了发电机的转速和输出功率的稳定性。因此，准确、及时地控制风力发电系统对于稳定发电机转速和输出功率、平滑桨距角、延长机械寿命、提高风电系统的可靠性等具有重要意义。

不同风速段采取的控制方法应是不同的，一种好的控制策略可以减小各种因素导致的功率波动，在能够快速追踪最大风能的同时保证功率的平滑输出。风力发电控制技术可大致分为三类：传统控制方法、智能控制方法和先进控制技术。文献[3]将模拟退火算法与爬山法相结合，分析了风速对输出功率的影响。文献[4]考虑高风速下功率和桨距角的关系，建立二者的灵敏度关系并设计变桨距控制器。变论域模糊偏航控制策略对风速扰动具有一定抑制作用[5]，但模糊界限设定主观性较大。文献[6]将PID与蚁群算法相结合，有效控制了额定风速以上风机的功率波动。

模型预测控制对于解决风电系统的强扰动、不确定性问题，减小载荷表现出显著的效果。预测控制在1997年较早地被提出应用于小型风力发电系统[7]，后来又提出将最大风能捕捉与预测控制相结合[8-9]。文献[10]采用简化线性模型的预测控制实现了大惯性风机的功率平滑输出。文献[11]将模型预测控制和神经网络的分段复合控制的方法相结合，优化了风力发电系统的多干扰、时滞性、非线性等控制问题，但相对较复杂。文献[12]针对变速恒频风力发电机易受风的随机性等特点的影响，设计了一种基于广义预测控制的新型变桨控制器，能够有效抑制风速干扰，输出恒定功率，计算量相对较大，运行时间较长。文献[13]将数据驱动和预测控制相结合，在降低了预测控制对系统预测模型的要求的同时，实现了额定风速以上系统的恒功率控制。MPC能够抑制输出功率的波动，但是可能增加能量的损耗[14]。

考虑到风速的不稳定性，风速变化是影响风机输出功率和转速的重要因素之一，并且大型风机桨距角变化受到机械惯性的影响具有短时的滞后性。因此，采取改进的隐式广义预测控制对风力发电系统进行优化控制。然后结合风速预测对桨距角做预补偿调整，以减少调整误差和桨距角过调整现象。为了提高系统的运行效率，对风速采取超短期预测，并将改进的隐式广义预测控制算法(Improved Implicit Generalized Predictive Control，Imp-IGPC)作为模型预测控制的基础算法，减少运算量的同时提高整体的运行效率。与传统控制方法相比，改进的隐式广义预测控制能够对风电机组未来状态做出预测，有利于平滑机组的输出功率；能够预知机组的控制指令，提前对桨距角进行调整，避免了桨距角的频繁调整和转速波动，并且可以通过约束条件防止参数超出范围。通过仿真实验验证了该控制方法的有效性。

1 风力发电系统模型

1.1 风机模型

根据空气动力学的原理可以得到风力机所获取的功率方程如下[15]：

(1)

式中，Cp(λ,β)为风能利用系数；λ为叶尖速比；β为桨距角；ρ为空气密度(在15℃的海平面平均气压下为1.225kg/m3)；R为风机风轮的旋转半径；v为输入风速。

由于桨距角的调整具有一定的滞后性，因此可以用带延迟的动态一阶系统来表示：

(2)

1.2 线性化系统模型

假设风力发电系统的叶片和塔筒都是刚性体，传动链是柔性体，采用风轮旋转和传动链扭振两个自由度建立风力发电系统的三状态线性模型。

风轮旋转的运动方程为可近似用一阶差分方程表示：

(3)

式中，Jr为风轮转动惯量，ωr为风轮的转速，Tr为风轮转矩，Tshaft为低速轴对应的反转矩。

风轮的转矩则可表示为

(4)

低速轴对应的反转矩Tshaft的方程为

Tshaft=Kd(θr-θg)+Cd(ωr-ωg)

(5)

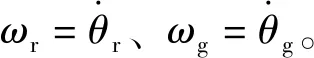
根据运动方程对Tr进行泰勒展开可得：

Tr=Tr(v0,ωr0,β0)+αδv+γδωr+ζδβ

(6)

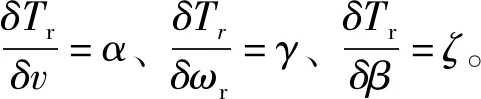
根据式(5)得低速轴对应的反转矩增量：

(7)

式中，Tshaft0为平衡状态时的转矩。由于在平衡点处风轮加速度为零，因此风轮转矩增量和低速轴转矩增量都为零：

Tr(v0,ωr0,β0)=Tshaft0

(8)

因此

(9)

忽略发动机本身的阻力，则其运动方程与风轮相似，在平衡点处发电机的加速度为零，推导公式也类似，可知：

(10)

联立式(9)和式(10)

(11)

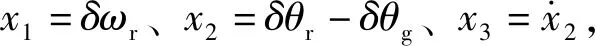
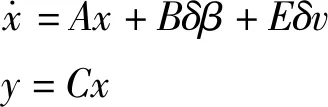
(12)

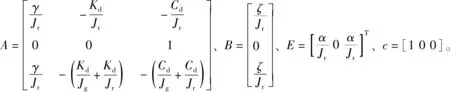
2 双馈风电机组隐式广义预测控制

2.1 隐式广义预测控制算法

GPC采用CARIMA(受控自回归积分滑动平均模型)模型作为预测模型，模型形式如下：

A(z-1)y(k)=B(z-1)u(k-1)+C(z-1)ξ(k)/Δ

(13)

其中，A(z-1)、B(z-1)和C(z-1)分别为n、m和n阶的z-1的多项式，Δ=1-z-1；y(k)、u(k)和ζ(k)分别为模型的输出、输入和均值为零的白噪声序列。

为了增强系统的鲁棒性，在目标函数中考虑了现在时刻的控制u(k)对系统未来时刻的影响，采用下列目标函数[16]：

(14)

式中，n为最大预测长度，m为控制长度(m≤n)，λ(j)为大于零的控制加权系数。

为了进行柔化控制，采取跟踪参考轨线的的方法，同时广义预测控制问题就转化为求Δu(k),Δu(k+1),…Δu(k+m-1)使得目标函数式(14)最小的优化问题。

由于GPC算法是先辨识对象模型，然后用Diophantine方程做中间运算，然后得到控制率参数，计算量较大，因此采取改进的GPC算法。GPC的最优化控制率为[17]

ΔU=(GTG+λI)-1GT(W-f)

(15)

式中，ΔU为控制增量，W为已知参考轨迹。由式(16)知，要求ΔU必须知道矩阵G和开环预测向量f。隐式自校正方法就是利用输入/输出数据，根据预测方程直接辨识G和f。

(16)

由式(16)可知，矩阵G中所有元素g0,g1,…,gn-1都在最后一个方程中出现，因此只需要对式(16)的最后一个方程进行辨识，即可求得矩阵G。

将式(16)的最后一个方程改写为如下形式：

y(k+n)=X(k)θ(k)+Enξ(K+n)

(17)

其中,X(k)=[Δu(k),Δu(k+1),…,Δu(k+n-1),1]θ(k)=[gn-1,gn-2,…,g0,f(k+n)]T

(18)

使用如下递推最小二乘公式估计θ(k)：

(19)

其中，λ1为遗忘因子，0<λ1<1。根据递推公式(19)得到θ(k)的估计值 ，即得到矩阵G和f(k+n)。

根据递推公式可得k时刻n步估计值：

y(k+n/k)=X(k)θ(k)

(20)

其中，X(k)=[Δu(k),Δu(k+1),…,Δu(k+n-1),1]。

已知GPC与DMC控制规律具有等价性，又知下一时刻的Y0向量为

(21)

式中，p为模型时域长度(p≥1)，h2,h3,…,hp为误差校正系数。e(k+1)=y(k+1)-y(k+1/k)为预测误差，故可知下一时刻的预测向量f为

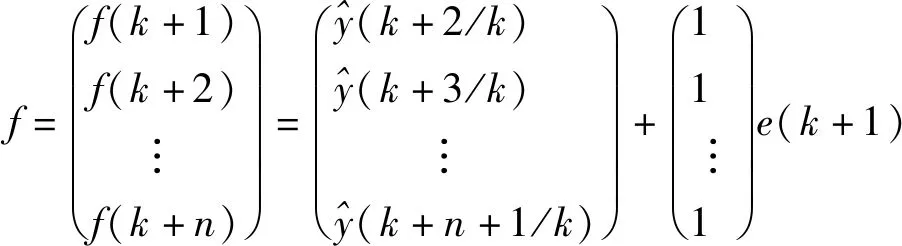
(22)

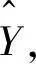
2.2 隐式广义预测控制器设计

风力发电机处于低风速段时，需要快速追踪最大风能；处于高风速段时，为使风力发电机能够发出额定功率，并且不超速，需要控制模块不断对系统发出变桨距的命令。由于桨距角的机械调整设备具有一定的滞后性，因此会产生桨距角变化不及时的现象，从而需要桨距频繁变化达到抑制有功功率和转速波动的目的。尤其在风速突降的时候，桨距角变化的延时会引起转速波动，风力发电机无法最大化利用风能，从而导致输出功率下降。为了能够改善由于桨距角变化慢而导致的功率下降的情况，同时能够抑制转速的变化以及平滑桨距角，提出一种改进的隐式广义预测控制。

本文提出的双馈风力发电机的改进隐式广义预测控制采用的是结合风速预测的隐式广义预测控制。控制系统结构框图如图1所示。

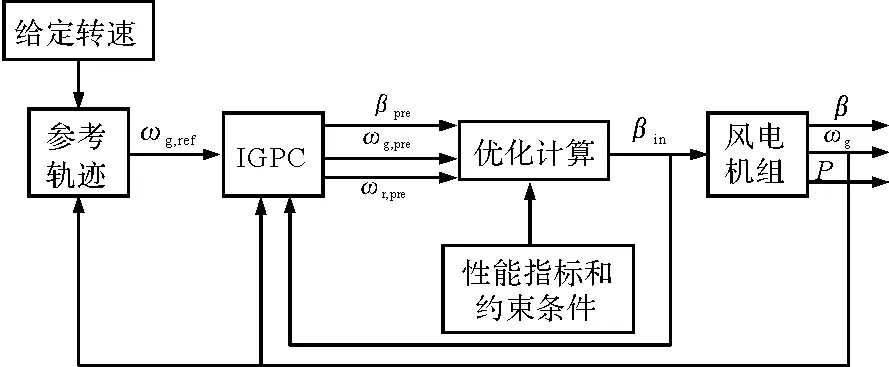
图1 隐式广义预测控制框图

图中ωg,ref、ωg,pre、ωg、ωr,pre、βpre、βin、β、P分别为发电机参考转速、预测转速、发电机实际转速、风轮预测转速、预测桨距角、优化后的桨距角、风机实际运行时的桨距角和实际输出功率。

前面给出了风力发电机的线性化模型和隐式广义预测算法。为了满足最小化控制标准，以发电机转速和桨矩角为控制变量，避免桨距角的频繁调整，维持电机的转速恒定，最大风能捕获和输出功率平滑为控制目标。根据式(14)可将下式作为目标函数

(23)

其中,

Δβmin≤Δβ(k+j)≤Δβmin
0≤ωg(k+j-1)≤ωg,maxPpre(k+j)≤Ppre,max

(24)

q(j)、λ(j)为权值系数。当风速小于额定风速时，采用最佳叶尖速比法追踪最大风能，将桨距角保持在0°，尽可能提高最大风能的追踪速度；当风速大于额定风速且发电机转速达到额定转速附近时，采用改进的隐式广义预测控制，主要目的是稳定转速和平滑输出功率，因此设置q(j)为较大值，λ(j)为适当量。

在此基础上，提出一种联系现在和过去控制量的方法，即当前控制量是现在和过去对现在时刻预测控制量的动态加权平均和的方法改善隐式广义预测控制的效果。

(25)

式中,bi为控制增量加权系数，可取为bi=1/ei，跟随每次的误差波动而波动(ei为k-i+1时刻预测结果与实际结果的误差值)。

图2为预测补偿控制。

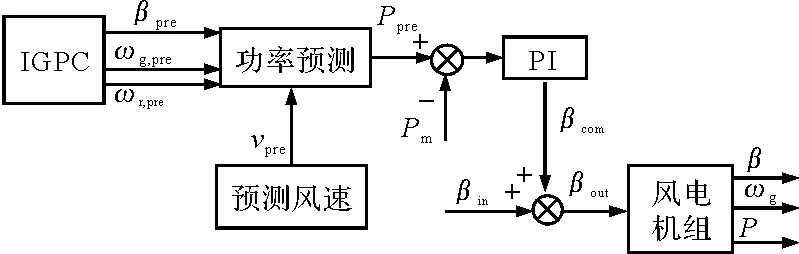
图2 补偿控制框图

Ppre、Pm、βout分别为预测功率、额定功率和实际给定风机的桨距角。

控制增量Δu(k),Δu(k+1),…,Δu(k+m-1)具有多个值，因此可以充分利用其滚动优化效果，对未来的功率进行多步预测，然后取平均值。

(26)

不同的风速段，风力发电机的输出功率目标是不一致的，因此本文采用两种运行模式：①当风速小于额定风速时，采用最佳叶尖速比法追踪最大风能，同时稳定功率的平稳输出；②当风速高于额定风速且转速达到额定转速附近时，采用本文提出的隐式广义预测控制方法提前改变桨距角，否则就采用模式①。在采用隐式广义预测的同时根据未来带五个采样点的风速和功率的预测给予桨距角的补偿，从而减小预测误差，使发电机转速与输出功率都稳定在额定值附近。

在模式切换方面，转速、功率以及风速都可以作为控制方法之间的切换判断标准。考虑到风速的随机性与波动性，为了避免控制方法的反复切换以及由此引起的功率和转速的波动，将采用转速和风速相结合的方法。首先是转速到达额定值附近，然后获取风速预测模块中紧接着的几个预测风速，对这些有限时间内的风速取平均值，再结合预测模型模块中的预测转速，共同对是否切换控制方法做出决定。

3 实验结果与分析

为验证本文所提的桨距角预补偿调控方法的可行性，在Matlab/Simulink中对1.5MW双馈风力发电机组进行仿真研究。其中预测时域为6，控制时域为3，为了更贴近实际以及方便预测补偿，选取采样时间为0.1 s，相应的Ppre为平均预测功率。具体风力机组数据如表1所示。

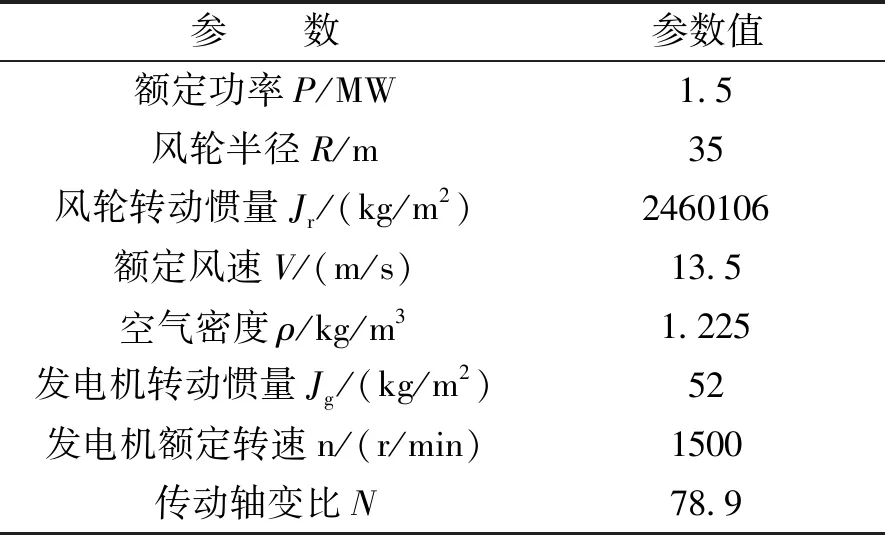
表1 风电机组参数

实验分别采用阶梯风速和高风速仿真，风力发电机采用初始为未起动状态，因此在前15 s左右是起动阶段，需要快速追踪最大风能。采用改进的隐式广义预测控制对未来时刻运行状态预测时需要进行超短期风速预测。

3.1 阶梯风速

图3所示为阶梯风速时的仿真结果，起始风速是10 m/s，每隔10 s增加2 m/s直至20 m/s，然后每隔10 s减少2 m/s。在额定风速以下时，三种方法都能够快速追踪最大风能，当风速从12 m/s突变到14 m/s时，风轮受惯性影响使得发电机转速延迟几秒到达额定转速，此时传统PI调节方式又受到桨距角调节滞后性的影响，出现了桨距角调整过大的现象，从而导致转速出现小幅度下降，而输出功率也相应地出现下，随后桨距角出现回落现象，产生了小幅度波动。隐式广义预测控制(IGPC)对此现象具有一定的优化作用，但是依旧会出现波动，相应的Imp-IGPC则能够抑制桨距角过调整的现象，减小了转速的波动从而平滑了输出功率，抑制了桨距角的频繁调整。

60 s后风速下降时从图3中可以明显看出传统PI调节方式受到桨距角调整滞后性的影响较大，发电机转速、输出功率和桨距角都出现了较大的波动。这是因为桨距角调整不及时，出现了无法最大利用风能的情况。对比PI调节，IGPC和Imp-IGPC都能够提前对桨距角进行调整，抑制了转速和输出功率的波动，Imp-IGPC的效果相比于前两者都更好。当风速从高于额定风速降到额定风速以下时三种方法都能够较好的实现功率输出。

从整体来看，PI控制下的桨距角都过产生过调整现象，导致了发电机转速和输出功率的波动，IGPC对此现象具有一定的抑制作用，Imp-IGPC则能够比前两者更好地实现抑制桨距角的过调整现象，从而达到抑制转速波动、平滑输出功率的目的。本文采用的模型切换也能够较好地实现切换的目的。

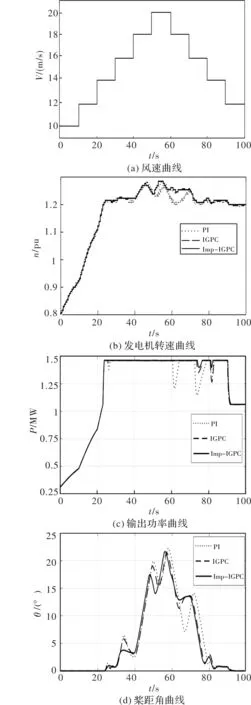
图3 阶梯风速仿真结果

3.2 高风速段

图4为高风速段三种控制方法所对应的不同测量量的控制效果对比图。

根据图4可以发现，对比传统的PI控制方法，IGPC和Imp-IGPC都能够对桨距角的调整做出提前预测，从而使其提前动作，抑制了桨距角的过调整和频繁变化(如图4(d)所示)。由于桨距角的提前动作，使得IGPC控制方法能够稳定风力发电机的转子转速，减小了由于风速过调整以及桨距角的滞后性所带来的转速波动。

相比于IGPC，改进的隐式广义预测控制能力更进一层，能够稳定转速在额定转速附近小幅度波动。由于风速波动和桨距角变化慢所导致的功率下降情况明显减少，且下降幅度也明显减小。尤其在风速较大，且突变明显的时间段(40～60s)，能够明显地发现，无论是稳定转速、平滑功率输出，还是抑制桨距角的过调整和频繁动作，改进的隐式广义预测控制(Imp-IGPC)的效果要优于传统PI控制和IGPC。

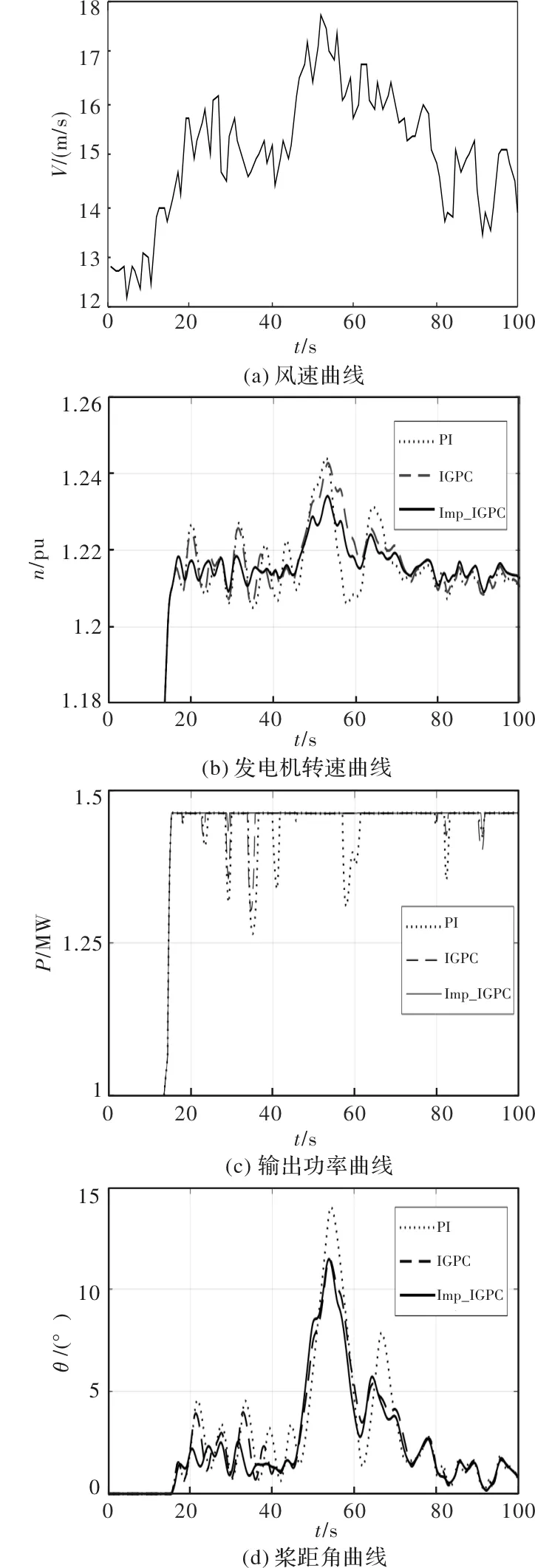
图4 高风速段仿真结果

4 结 语

针对双馈风力发电机的桨距角调整具有滞后性，及其导致的转速和功率波动问题，本文提出使用隐式广义预测控制对双馈风力发电机进行预测控制，在此基础上结合算法内不同时刻对同一时刻点的预测，对隐式广义预测输出进行优化，并将其与风速预测补偿共同应用于双馈风力发电预测控制。仿真结果表明，与传统的PI控制方法相比，所提控制方法具有更好的动态特性。发电机转速波动明显降低，变桨机构能够更快速、更准确的变桨，抑制了过调整和频繁调整，同时抑制了输出功率的波动，减少了由于风速突变和桨距角滞后带来的功率降低的情况。综上，该方法有利于机组在额定状态平稳运行，维持电网可靠性，并调高风机使用寿命。