风力发电机组最优桨距角自寻优控制算法设计

兰杰， 林淑， 莫尔兵， 王其君

(东方电气风电有限公司， 四川 德阳， 618000 )

0 引言

风能作为一种清洁可再生能源, 越来越受到世界各国的重视。 其蕴藏量巨大, 全球风能资源总量约为2.74×109MW, 其中可利用风能为2×107MW[1]。在风电大规模发展的今天, 机组运行效率越来越受到关注。 但目前风力机风能利用效率较低,对其发展极为不利。 当前, 如何充分利用风能资源实现风电机组发电量最大化是风电场运行过程中亟待解决的问题。 目前最行之有效的方法是通过有效控制策略使风电机组运行在最优状态来最大限度地捕获风能, 达到风电机组发电量最大化的目的, 该方法与其他方法相比更具有有效性和可行性。

文献[2-4]简述了风力发电机组最大功率跟踪控制策略； 文献[5-7]提出了风力发电机组最大风能追踪及变桨控制；文献[8]提出了基于支持向量和微分进化算法的风电机优化运行, 实现了风机出力最大化； 文献[9]提出了基于微分跟踪器的功率曲线自寻优控制策略, 提高低风速区域对风能的利用。 然而以上传统的最大风能捕获控制方法通常存在一些弊端, 风力机桨距角常常被假定控制在其最优值来使风力机的功率系数最大, 实际情况而言, 风力发电机组叶片在设计、 制造、 现场安装和实际运行过程中, 可能出现以下情况： 即叶片设计过程中, 理论最优桨距角和生产图纸有误差； 叶片制造过程中, 制造误差或者叶片零刻度盘位置贴错； 叶片现场安装过程中, 叶片零位未与轮毂零位对齐； 叶片经过较长时间运行后,气动性能发生改变, 最优桨距角不再是模型设计时的最优桨距角； 此外, 运行人员操作过程中产生的错误等。 上述使得最优桨距角偏离的原因是很难避免的, 且在实际风力机中并不是一个固定的偏移量, 不同风机可能有不同的偏差值, 很难用同一个偏移修正量去修正。

为快速、 有效寻找最优桨距角, 本文以国产某1.5 MW 机组为基础, 充分利用其数据之间的相关性, 设计出一种自动寻优控制算法, 构造出桨距角评价函数, 能够自动寻找出实际的最优桨距角, 为提高风力发电机组性能提供了科学依据。

1 风力机能量转换原理分析

风力机将风能转化为机械能并带动发电机发电, 为实现风电机组变速运行, 追求最优Cp曲线。 Cp（λ,β）为风轮的利用系数, 反应了风力机利用风能的效率, 它是叶尖速比与桨叶节距角的函数。 根据文献[10]风轮的尖速比经验公式为式（1）：

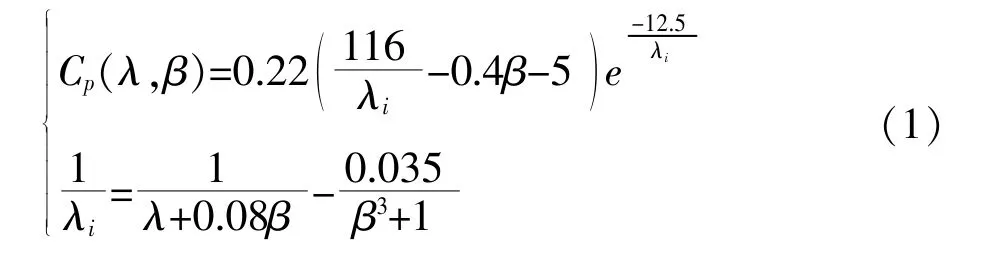
一般通过改变发电机扭矩控制发电机转速,由风力发电机组能量转换系统（见图1）可知：

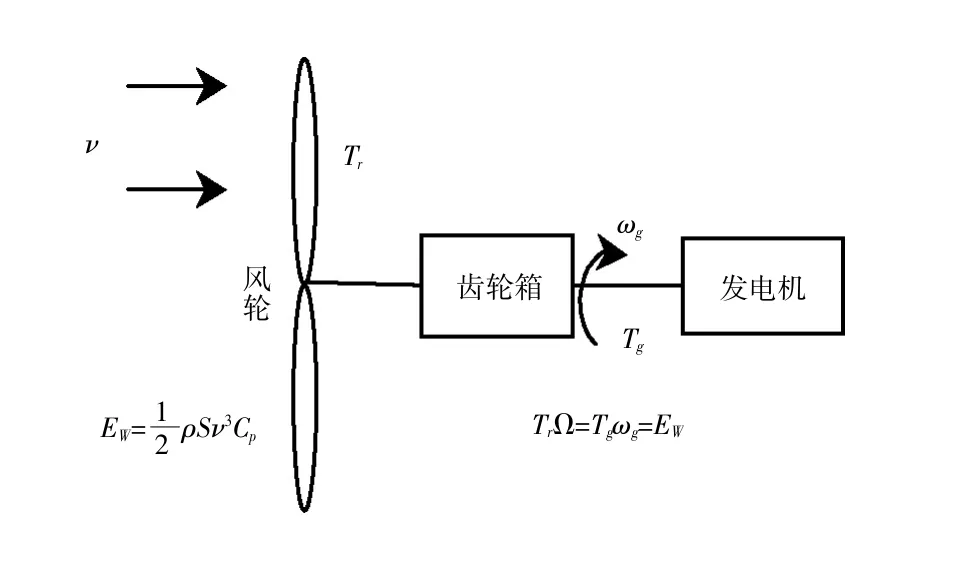
图1 能量转换系统

为使风轮运行在最优转速上, Ωopt有如下转换方式：

式中： Ωopt为风轮最优转速； λopt为最优叶尖速比； Cp（max）为最优风能利用系数； ωg（opt）为最优发电机转速； N 为齿轮箱变速比； Tg为发电机转矩；Kopt为最优模态增益。

式（3）说明, 只要将发电机转矩按照转速的二次方进行设置, 便能实现最优转速运行, 使风电机组运行在最优Cp曲线上。

为了能够自动寻找最优桨距角, 需要得到在不同桨距角下的功率曲线, 如图2 所示, 从而进行对比, 得出最优桨距角。

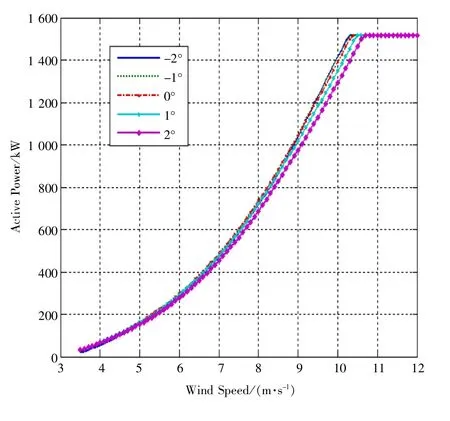
图2 不同桨距角时的功率曲线

但是实际测量过程中, 10 min 平均风速, 很难完全一样, 即使平均风速一样, 由于其湍流强度不同, 可能会导致测量到10 min 平均功率不同, 通过Bladed 仿真结果如表1～3 所示。

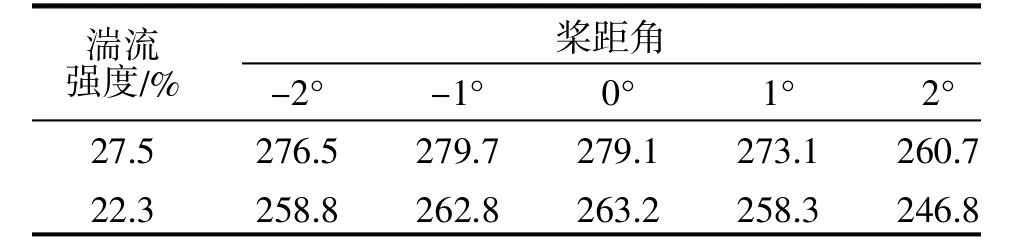
表1 平均风速5.8 m/s 时10 min 平均功率（kW）对比

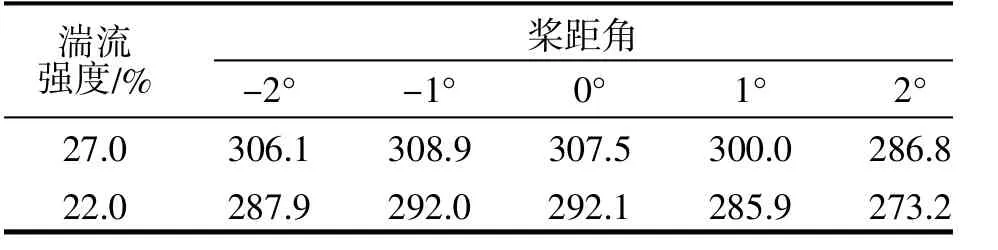
表2 平均风速6.0 m/s 时10 min 平均功率（kW）对比

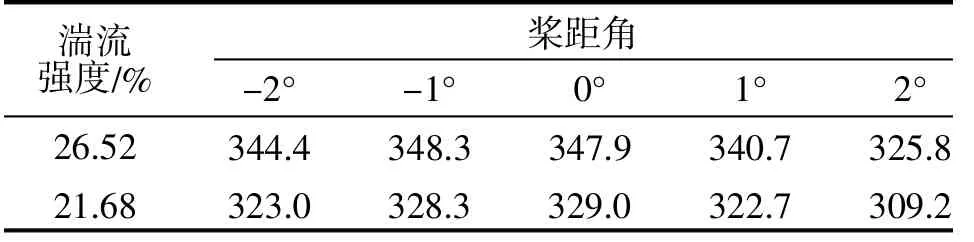
表3 平均风速6.2 m/s 时10 min 平均功率（kW）对比

从表1～3 可以得出如下结论：

（1）相同最优桨距角,不同平均风速时,10 min平均功率差别很大；

（2）相同最优桨距角, 相同平均风速下, 不同湍流强度下, 10 min 平均功率有差别；

（3）不同湍流强度, 最大平均功率所对应的最优桨距角不同；

综上, 不能简单以平均风速所对应的平均功率大小来简单评判最优桨距角, 在风机运行过程中, 很难有完全相同的工况, 即相同的平均风速和相同的湍流强度。 为了达到有效的功率曲线,需要累积足够多的样本, 因而需要较长时间的测试运行, 才能得出较合理的统计功率曲线。 为了降低所需样本数量, 减小测试运行时间, 应该综合考虑湍流强度、 平均风速的影响。

2 理论分析

针对风力发电机组, 当风机叶片最优桨距角设置为不同值时, 其理论功率值也会不同, 具体如表4 所示。

表4 不同桨距角时的理论功率（kW）

从表4 可以看出, 桨距角不同时功率曲线具有以下特点：

（1）变速运行阶段为5～8.5 m/s, 此时0°为最优桨距角；

（2）其余风速情况下桨距角为0°时功率曲线并不是最大。

进一步通过现场实测数据分析, 可以发现一段时间内（通常选取为10 min）风速的分布近似具有正态分布特性, 结果如图3 所示。

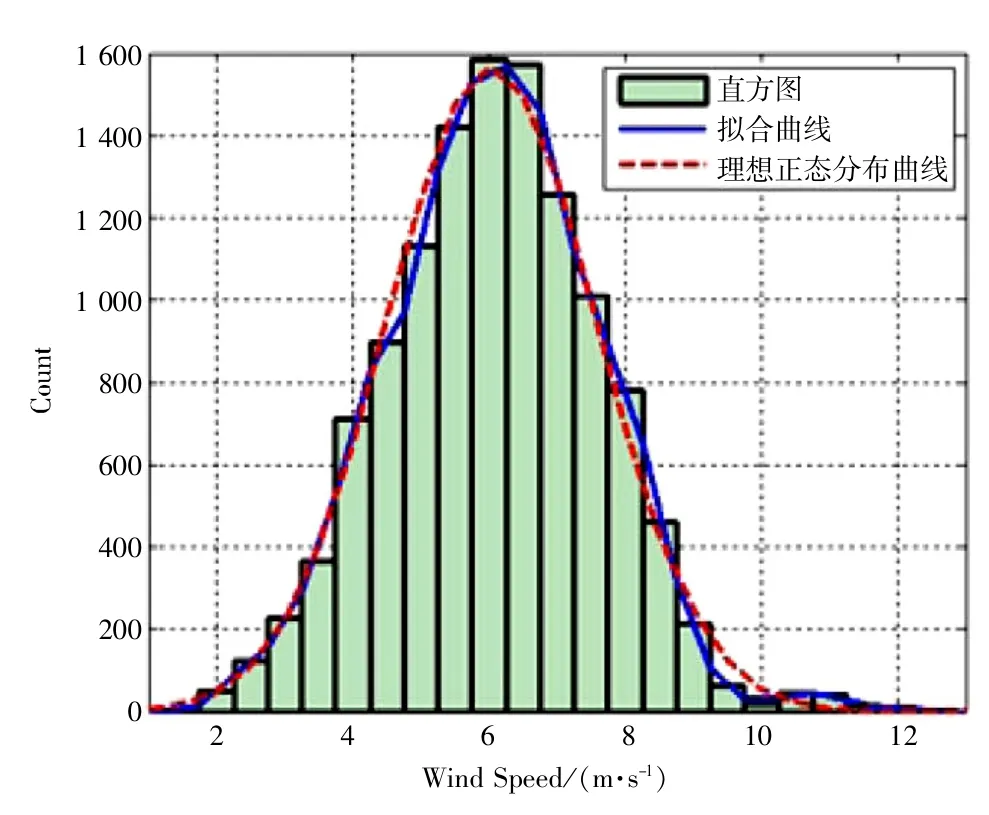
图3 风速分布曲线

因此, 可以用正态分布来表示风速的分布情况, 也可以通过计算风速的平均值和方差来表征风速的分布情况, 即：

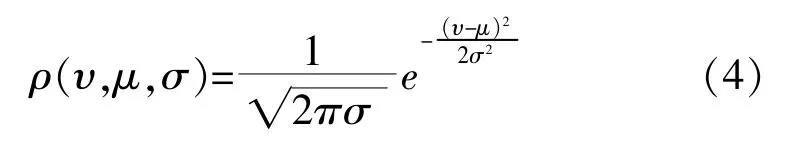
式中： υ 为风速； μ 为均值； σ 为方差。

假定风力发电机组工作在最佳状态, 风速和功率呈对应关系, 则可以用如下积分来表达一定平均风速、 方差下的理论平均功率：

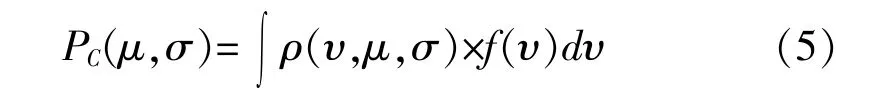
式中： υ, μ, σ 意义与式（4）相同；f（υ）表示风速对应功率函数。 典型的静态功率曲线f（υ）如图4所示。

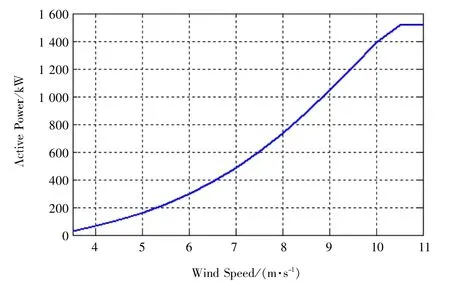
图4 典型功率曲线

由式（5）就可以计算出对应平均风速和方差下的理论平均功率PC（μ,σ）, 其计算结果也就包含了湍流信息。 而实际平均功率PM（μ,σ）也包含了风速湍流信息, 因此通过PC（μ,σ）和PM（μ,σ）构造新的评价函数, 来自动寻优最优桨距角。

3 自寻优算法设计

考虑到实际运行风机大多采用机械式风速仪测量风速, 由于其受叶片尾流影响, 得到风速具有较大误差, 而测量到功率相对较为准确, 因此做如下假设：

风速测量具有固定偏差, 则实际风速为：

式中： υA为实际风速； υM为测量风速； Δυ 为风速测量偏差。 因此通过υM得到的平均风速也具有偏差Δυ, 但计算得到的方差却无偏差, 即：

式中： μA为实际平均风速； μM为测量平均风速； σA为实际风速方差； σM为测量风速方差。

功率测量较为准确, 因此实际功率为：

式中： PA为实际功率； PM为测量功率。

假设构造的评价函数为F （PC,PM）, 该函数也是μA和σA的函数, 即H（μA,σA）, 因此把式（7）带入可得：

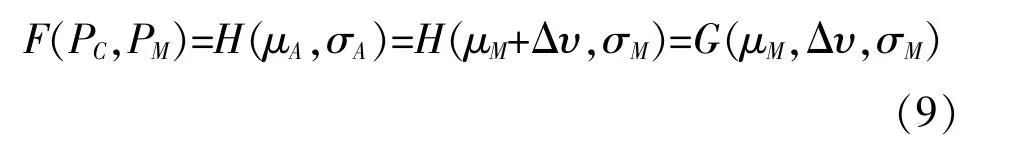
而构造的评价函数G（μM,Δυ,σM）需具有一定的稳定性, 即当Δυ 在一定范围内波动时, 通过评价函数能得到相同的结果。 由式（5）可知, 积分是一个超越函数, 没有一个简单的Δυ 与F（PC,PM）的关系, 因此直接构造PC（μ,σ）和PM（μ,σ）评价函数难度很大。

考虑从测量准确的功率和风速方差出发, 计算出在方差σ 已知时, 发出电功率为P 时所需的平均风速μC为多大, 因此μC中也含有方差的信息, 再通过构造包含μC和μA的评价函数即可, 因此最终构造的评价函数如式（10）所示：

由式（10）定义很容易推得, 当评价函数更大时, 对应的桨距角为更优的桨距角。

把式（7）带入式（10）可得：

进一步分析计算结果的稳定性, 设：

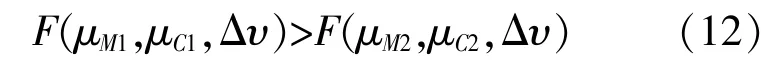
把式（11）带入式（12）可得：

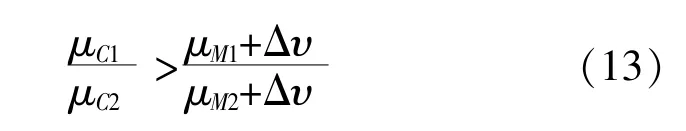
从式（13）可以看出, 当测量风速的固定偏差在一定范围内时, 利用连续函数的保号性, 可以得到以下等价关系：

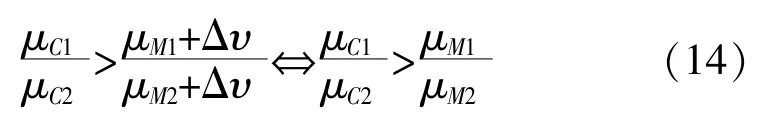
因此Δυ 在一定范围变化时, 式（9）所定义的评价函数则是稳定的。

具体的自寻优控制框图如图5所示。

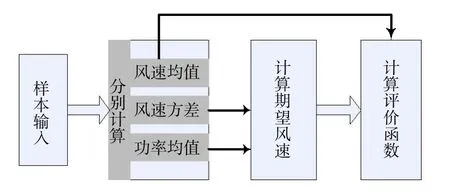
图5 自寻优控制框图

为了能够完成桨距角自动寻优, 需要能够自动调整最优桨距角, 再按照图5 所示算法计算所有可能成为最优桨距角的评价函数, 最终得出实际的最优桨距角。 其算法流程如图6 所示。

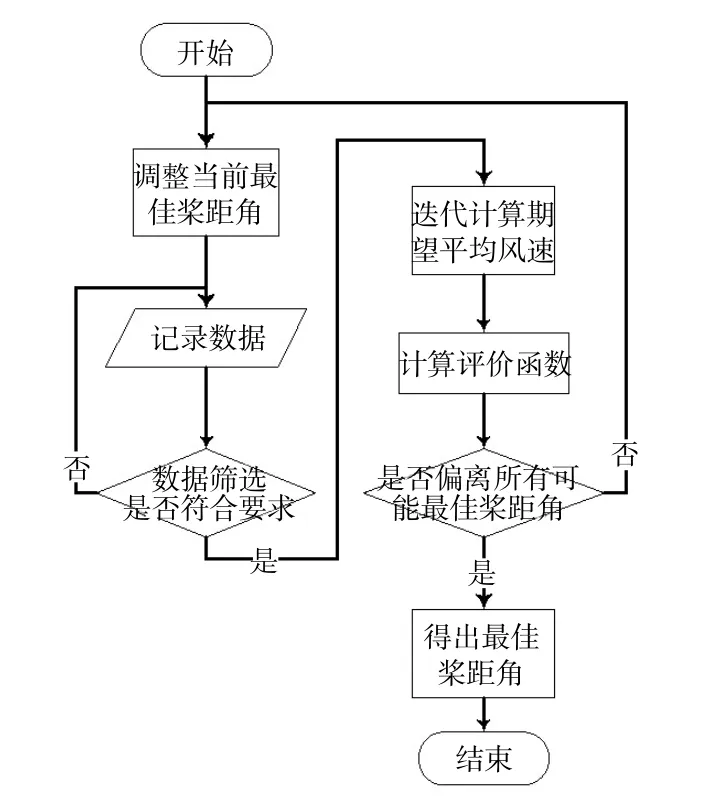
图6 自动寻优流程图

4 仿真分析

本文采用某国产1.5 MW 风力发电机组, 建立Bladed 模型, 模型假设最优桨距角为0°。 通过设置桨距角到分别在0°、 ±2°, 且在不同工况下进行仿真验证对比, 仿真结果如表5～8 所示。

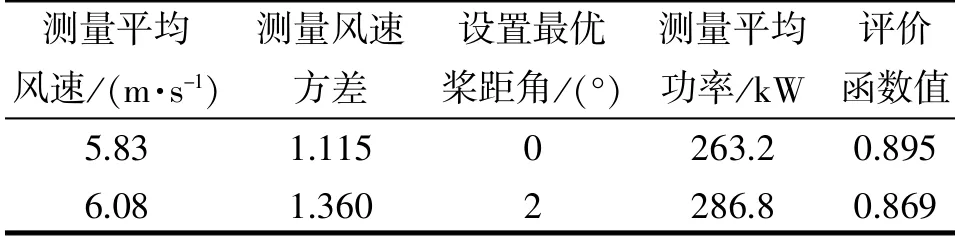
表5 结果对比1

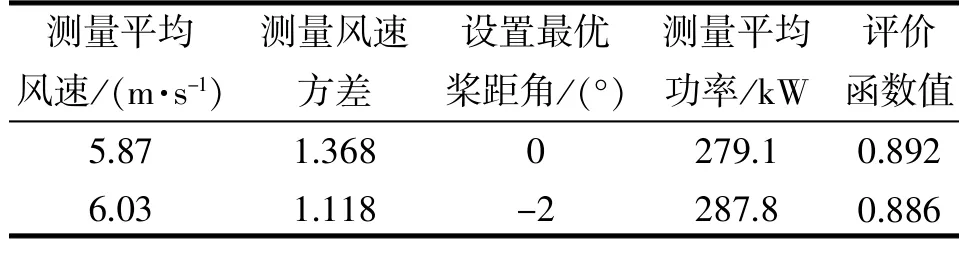
表6 结果对比2

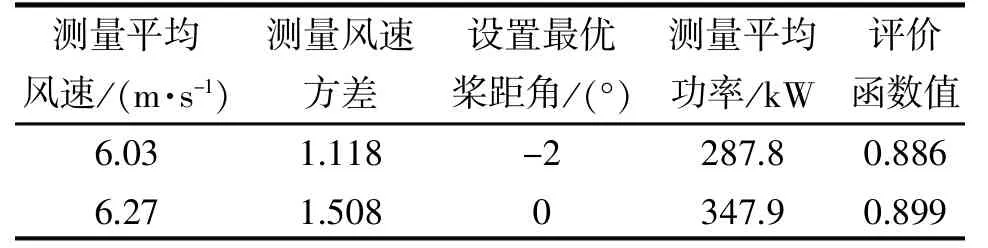
表7 结果对比3

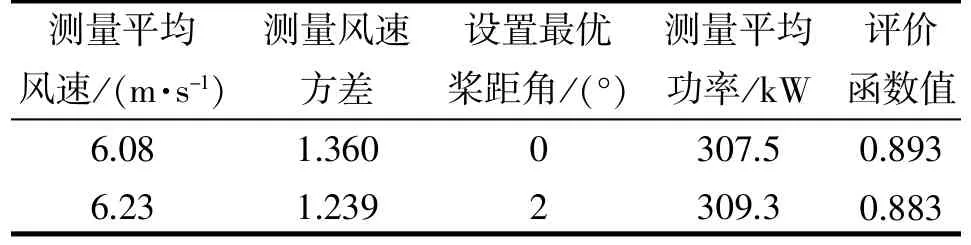
表8 结果对比4

从表5～8 可以得出, 当设置最优桨距角为0°时, 均具有最大的评价函数计算值, 因此寻优结果得出0°为最优桨距角, 而模型假定最优桨距角确实为0°, 验证本文设计的自寻优算法能够准确寻找出实际最优桨距角, 证明该算法的有效性、快速性, 为提高风力发电机组的性能提供了科学的指导。

5 结论

本文以国产某1.5 MW 风力发电机组设计为例,仿真结果表明, 所提出的自寻优控制算法能够自动寻找出实际的最优桨距角, 为提高风力发电机组的性能提供了科学的指导。