基于模糊磁链转矩估算器的滑模DTC设计

王福杰

(山东得普达电机股份有限公司，山东 淄博 255200)

0 引 言

永磁同步电机(PMSM)具有高可靠性、高功率密度及高效性等优点，广泛应用在电动汽车的驱动领域。为满足电动汽车高调速范围，以及在复杂工作环境下对转矩控制快速响应，提出了一种基于模糊磁链估计器的滑模直接转矩控制技术(Direct Torque Control, DTC)[1-3]。DTC是永磁同步电机主流的交流变频调速技术之一，其控制算法相对于矢量控制计算简单且降低了算法对于电机参数的依赖性。然而传统的DTC是分别对转矩误差及磁链误差进行调整控制，实现转矩快速响应，但是会造成大幅度的磁链和转矩脉动，电机在低速高负载运行时的控制精度低[4]。针对这一缺点，学者提出了一种滑模控制器[5-8]，有效的解决了DTC在电机低速时产生的磁链转矩抖动较大的缺点，逆变器开关频率不恒定的问题。滑模DTC的控制精度受到磁链转矩估计器的影响，本文提出了一种模糊磁链转矩估算器，采用模糊控制的方法获得磁链估计所需的定子电阻值，从而提高磁链的估计精度，改善滑模控制的精度。采用模型参考自适应系统(Model Reference Adaptive System, MRAS)获得转子位置及转速反馈到滑模DTC中[9-11]，实现高效闭环控制的同时提高驱动系统的可靠性。

1 基于模糊磁链转矩估算器的滑模DTC

本文提出的基于模糊磁链转矩估算器滑模DTC控制系统控制框图如图1所示，该系统由三部分构成：模糊磁链转矩估算器、滑模控制器、MRAS。

模糊磁链转矩估算器由磁链计算公式及模糊定子电阻估计器构成，主要作用是为滑模控制器提供精确的磁链反馈提高控制精度。模糊定子电阻估计器通过实时采集电压信号，经过模糊模块调节间接改变当前周期状态下的电子电阻值，将该值反馈到磁链转矩估计公式。

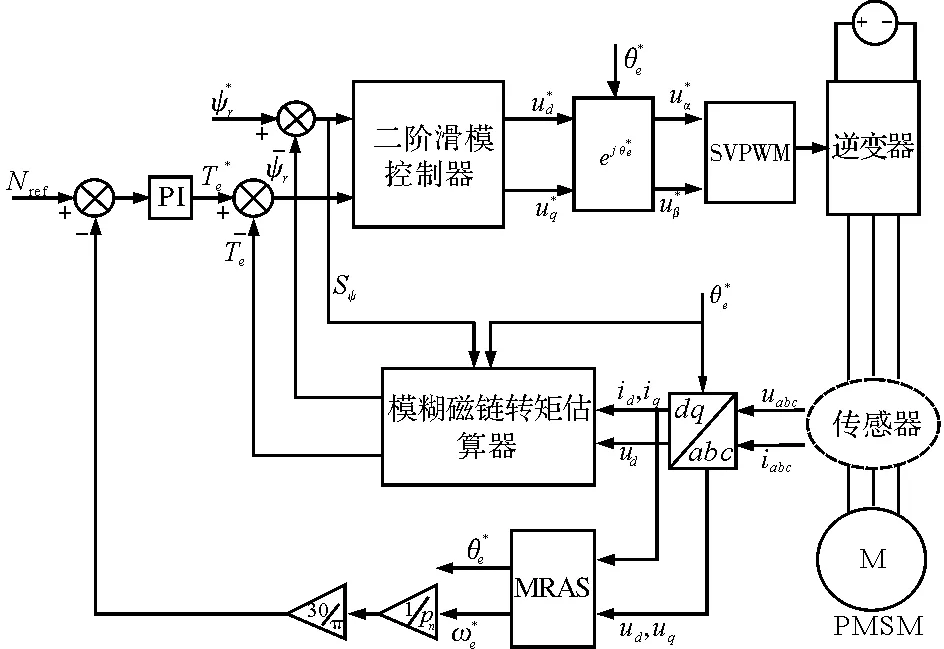
图1 基于模糊磁链估算器滑模DTC控制系统

滑模控制器可以提高逆变器的开关频率，使控制周期内的有效电压矢量接近期望电压矢量，有效降低磁链和转矩脉动。

通过模型参考自适应系统获得电机转速的估计值，将期望模型与可调模型输出量之差经过合适的自适应率实现对电机转子位置的估算。

1.1 模糊磁链转矩估算器

模糊磁链转矩估算器由磁链转矩估计公式和模糊定子电阻估计器构成。由于电动汽车永磁驱动系统需适应多种工况，故定子电阻参数是随机变化的，从而降低了磁链转矩估算器的运算精确性。考虑定子电阻变化量与磁链变化之间的关系是一个复杂的非线性关系，固定模型表述方法难以实现，本文采用了模糊控制方法实现定子电阻估计，通过采集磁链误差，利用模糊规则对电子电阻进行补偿的同时间接的改善了定子磁链调节。模糊磁链转矩估算器结构框图如图2所示。

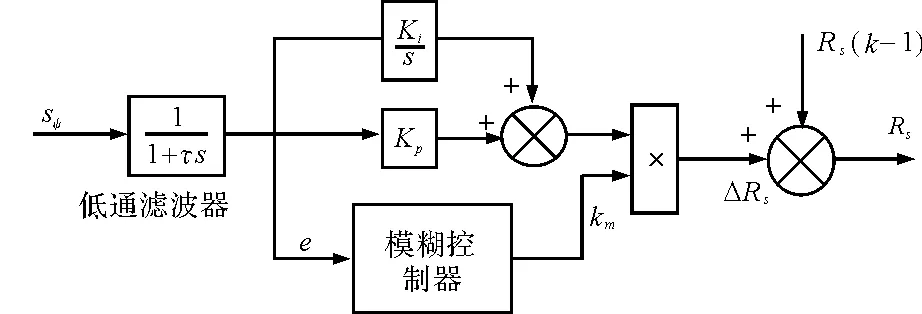
图2 模糊定子电阻估计器控制框图

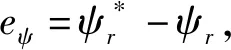
(1)

式中，T为采样周期，Kp，Ki为比例增益，积分增益；km为模糊校正系数。

表贴式三相PMSM的数学模型表达式如式(2)所示：

(2)

ψr=ψf+Lsir

(3)

式中，ψf为永磁体磁链；Rs为定子电阻；Ls为定子电感；ψr为定子磁链空间矢量；ir为定子电流空间矢量；ur为定子电压空间矢量。

电磁转矩如式(4)所示，式中pn为电机的极对数。

(4)

当定子磁链矢量的方向与d轴方向一致时即(ψr=ψd=ψr时)，磁链的幅值估计计算公式如式(5)，式中Rs取至模糊定子电阻估计器。

(5)

1.2 二阶滑模控制器

将定子磁链误差定义为滑模面函数：

(6)

采用基于Super-twisting算法的二阶滑模控制原理，可以将磁链控制器表述为式(7)。通过改变式中的Kn,Km实现理想的控制效果。同理，令转矩误差为转矩滑模面函数为式(8)。

(7)

(8)

可将转矩控制器表述为式(9)。本文采用二阶滑模控制器，及r=0.5。因此二阶滑模控制器的控制框图如图3所示。

(9)

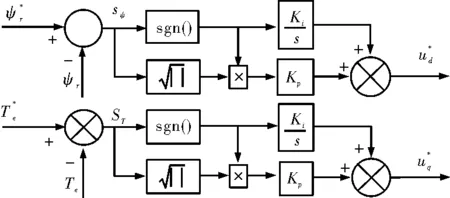
图3 二阶滑模控制器控制框图

1.3 模型参考自适应系统

MRAS算法本质上属于自适应系统的一种，该控制算法的结构框图如图4所示。由三部分构成：可调模型，参考模型及自适应律[12]；其中参考模型需要选择不含未知参数模型，含需要辨识未知参数的模型作为可调模型，采集两个模型的误差通过自适应机制调节改变可调模型中的参数，使输出跟踪参考模型[13-14]。该模块设计的核心是自适应机制的设计。本文的设计中将PSMS模型作为参考模型，含有带估计定子电阻的电流模型作为可调模型。

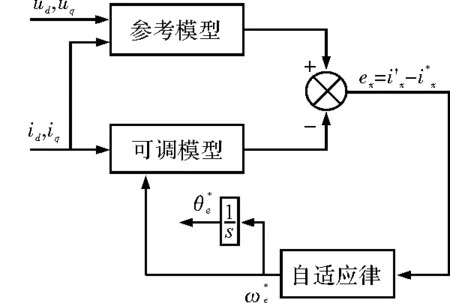
图4 MRAS控制算法的结构框图

表贴式三相PSMS的电流方程如式(10)：

(10)

式中：

(11)

式(10)的状态空间表达式为式(12)，作为可调模型。

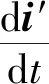
(12)

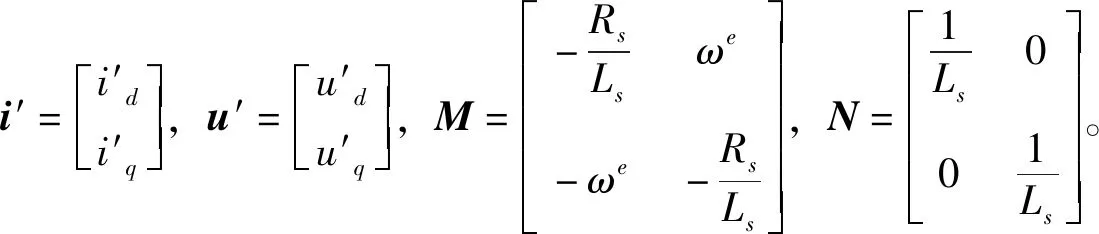
(13)

(14)

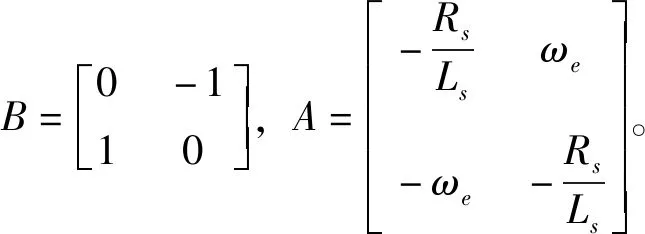
设计中机械时间常数远远大于电气时间常数，所以A中的参数ωe可视为数字控制系统中的一个不变参数。可以采用基准反馈系统Popov超稳定性理论作为自适应律。根据Popov的稳定性定理，获得自适应律：

(15)

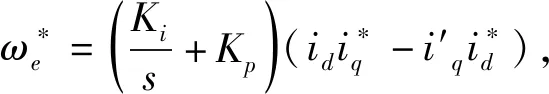
(16)

对式(15)求积分可得转子位置估计值

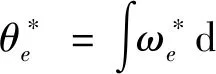
(17)

2 仿真对比

为验证本文所提算法的可行性及有效性，搭建了Matlab/Simulink仿真模型，将采用本文所提的控制系统与传统直接转矩控制方法进行仿真对比。仿真实验中所用PMSM参数如表1所示。

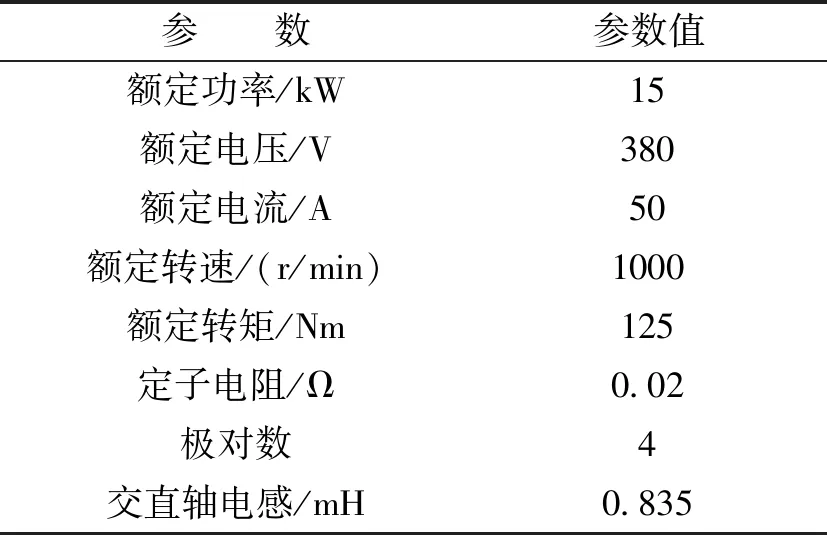
表1 仿真实验PMSM相关参数

模拟电机工作环境的温度发生变化时，定子电阻阻值于0.2 s时刻由0.02变为0.05时，并于0.3 s时刻恢复原值，提出的模糊磁链转矩估算器会对定子电阻估计值做出补偿，优化定子磁链的估计值使其接近实际值。仿真图如图5所示，图5(a)为采用传统直接转矩控制时定子电阻变化对磁链估计的影响，图5(b)为采用模糊磁链转矩估算器获得的定子磁链估计值。

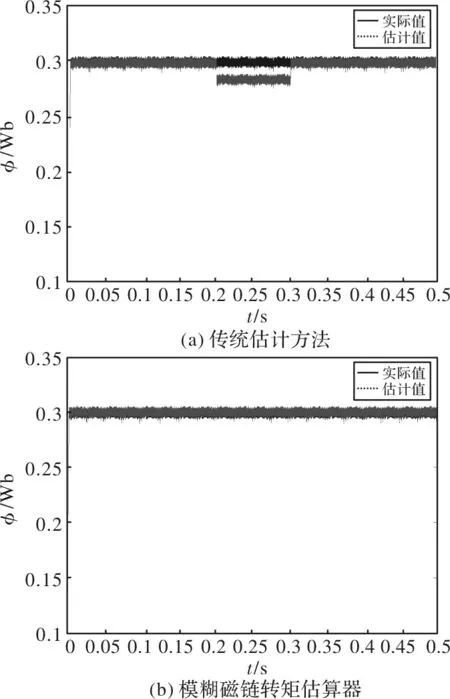
图5 模糊磁链估算器对定子电阻变化的响应

图6为PMSM在负载突变时改进控制系统对输出转矩脉动的抑制响应图，仿真于0.12 s时刻负载变为额定负载的5%，于0.25 s时刻负载变为额定负载的10%，0.3 s时刻结束仿真。仿真验证了提出的控制系统在负载稳定状态对转矩波动抑制效果明显，在负载波动干扰的过程中可以保证转矩脉动抑制的有效性。

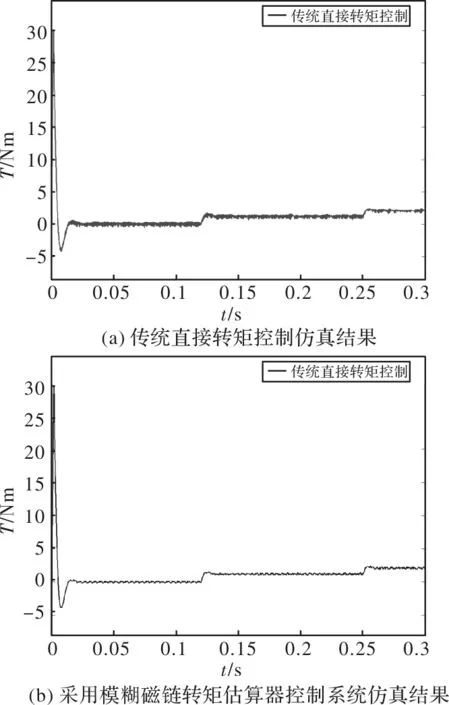
图6 本文提出控制系统对转矩脉动的抑制响应对比

为验证本文提出的控制系统对转子速度波动的抑制效果。进行了负载干扰状态下转速波动抑制响应仿真。对比仿真结果图如图7所示，仿真于0.3 s时发生外界干扰负载突由额定负载的10%变为30%，0.5 s时刻仿真终止。提出的控制系统有效的抑制转子速度的脉动，转速控制可在0.02 s内消除负载突变带来的干扰，验证了控制系统对转速控制的优化效果。

图7 本文提出控制系统对转速脉动的抑制响应对比

3 结 语

为了改善电动汽车驱动电机的控制性能及可靠性。本文提出基于模糊磁链估算器的滑模DTC控制系统，采用模糊定子电阻估计器优化磁链幅值估计的精确程度，进而优化了二阶滑模控制；控制系统采用MRAS算法估计转子位置与转速代替传统转速传感器，降低硬件成本的同时提高了驱动系统的可靠性。仿真结果验证本文所提出控制系统可以有效的抑制转矩及转速的脉动，并精确高效的控制电机转速，具有良好的稳定性。