基于数据驱动的风电机组最优桨距角 辨识方法

柏文超，刘颖明，王晓东，高 兴，张书源

（沈阳工业大学 电气工程学院，辽宁 沈阳 110870）

0 引言

在“双碳”政策背景下，风电行业的发展模式正逐步向精细化、集约化发展模式转变，行业研究关注点已经集中到增功提效方面[1]。

当风电机组运行在额定风速以下时，通常认为叶片方位位于0°是最优桨距角位置；此时，风能利用系数达到最大，输出功率最大[2]。然而，受叶片安装误差、机组外界运行环境变化等因素影响，机组运行时会发生最优桨距角与理论桨距角不一致的情况，从而造成风能利用率的下降；所以，需要对最优桨距角的位置（可正可负）进行研究[3]。

辨识最优桨距角，对提升风电机组发电量具有一定的价值和意义。

为快速找到风电机组最优桨距角，文献[4]提出了一种自寻优算法。由于用该方法构造的桨距角评价函数不具有稳定性，所以当风速波动剧烈时，得到的结果误差较大。

文献[5]考虑空气密度因素，提出了一种通过调整风电机组安装角的方法来增大机组输出功率。该方法的应用仅限于定桨距风电机组，且未考虑额定风速以下机组发电量。

文献[6]针对叶片安装角存在人为误差的问题，通过设置不同的安装角来对其进行模拟，并以此研究了安装角对风电机组性能的影响。但是，文中只分析了安装角误差对机组性能的影响，并未提出针对性解决方法。

为达到提升机组发电量的目的，本文提出一种基于运行数据驱动的风电机组最优桨距角辨识方法：首先，用拟合方法得到机组“风速-功率-桨距角”连续三维特性曲面，然后求解三维特性曲面变量之间的函数关系，进而辨识出不同平均风速下风电机组最优桨距角。

1 数据驱动辨识框架

风电机组桨距角对输出功率的影响如图1所示。从图1可以看出：在同一风速下，不同桨距角对应的输出功率不同。所以对于不同工况，可以通过改变机组桨距角的大小提升发电量。

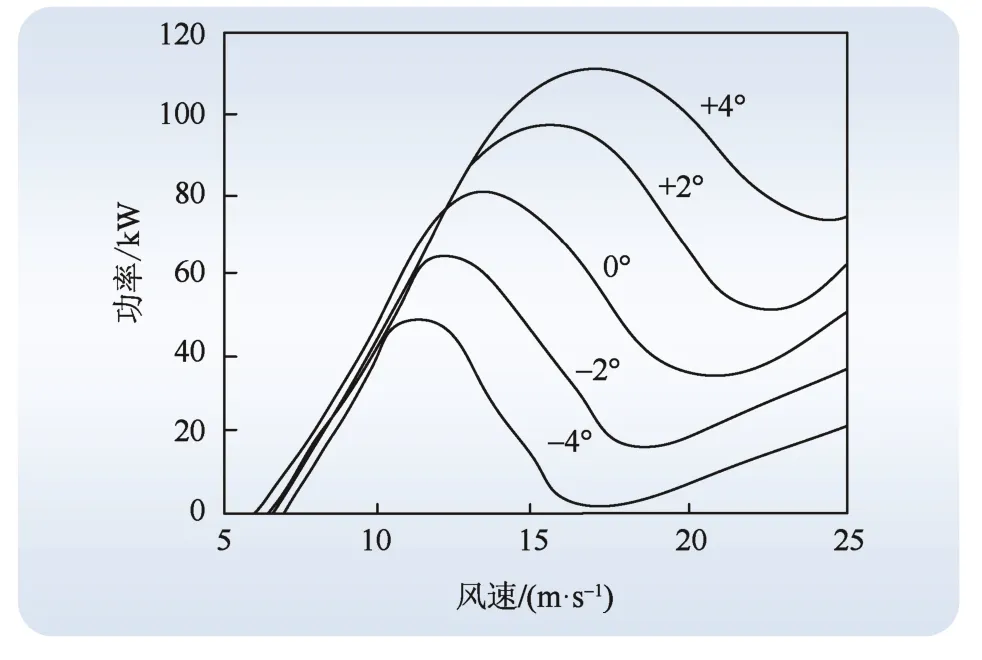
图1 桨距角与功率的关系 Fig. 1 Relationship between pitch angles and power

文本提出的风电机组最优桨距角辨识方法流程如图2所示，主要分为4个部分：异常数据清洗、三维特性曲面拟合、最优桨距角辨识和修正后发电量提升验证。

图2 风电机组最优桨距角辨识流程 Fig. 2 Identification process of optimal pitch angle of wind turbines

（1）异常数据清洗：为了消除异常数据点对整体分布规律和各变量间对应关系的影响，需要对初始数据进行预处理。首先剔除机组停机和故障时间段内无意义的数据；然后基于改进的DBSCAN聚类算法对“风速-功率”“风速-桨距角”等变量的离群数据及边缘数据进行识别并剔除；最后针对机组输出功率的多影响因素耦合问题，对数据进行标准化处理，消除机型、量纲、空气密度等因素的影响。

（2）三维特性曲面拟合：为了减小离散采样数据误差，首先提取预处理过后的机组“风速-功率-桨距角”散点图；然后，基于最小二乘法曲线曲面拟合方法，建立机组实际运行的“风速-功率-桨距角”连续特性曲面。

（3）最优桨距角辨识：为了辨识不同平均风速下最优桨距角，首先，通过LM（Levenberg- Marquardt）算法求解三维特性曲面变量函数关系；然后，以1 m/s为步长，通过辨识得到不同平均风速下风电机组最优桨距角。

（4）最优桨距角修正后的发电量提升验证：为了验证所提方法的有效性，首先在Bladed中对同一机组桨距角数值进行修正并验证；然后，将该机组模型提取到MATLAB中，在相同工况下再次进行验证。

2 基于运行数据的辨识算法

2.1 基于DBSCAN算法的离群数据剔除

考虑风电机组主要特征量的相关性，选择风速、功率、桨距角3个变量进行最优桨距角辨识。“风速-功率-桨距角”三维特性散点图如图3所示。

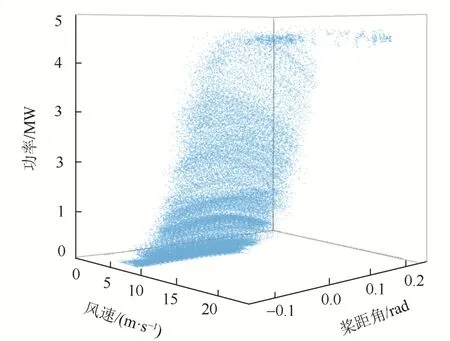
图3 初始数据三维特性散点图 Fig. 3 3-D characteristic scatter diagram of initial data

从图3可以看出，运行数据中存在一定量的异常数据，其中包括离群数据及边缘数据。异常数据产生的主要原因包括[7]：

（1）阵风或者控制器延迟。此类异常数据量大，为非稳态数据点，一般分布在正常数据簇周边。

（2）风电机组故障。此类异常数据较多，一般偏离正常数据且呈聚集分布。

（3）电磁干扰或者通信故障。此类异常数据量少，一般表现为离群数据。

在进行机组特性曲面拟合之前必须清洗初始数据，否则异常数据的存在将会严重影响运行数据的整体分布，导致变量间函数关系误差较大甚至错误。为了得到更准确的数据，初始数据点中的边界点和噪声点也被看作是异常数据。

DBSCAN算法基本流程图如图4所示，算法中半径Ep和邻域密度阈值Mp是给定的。

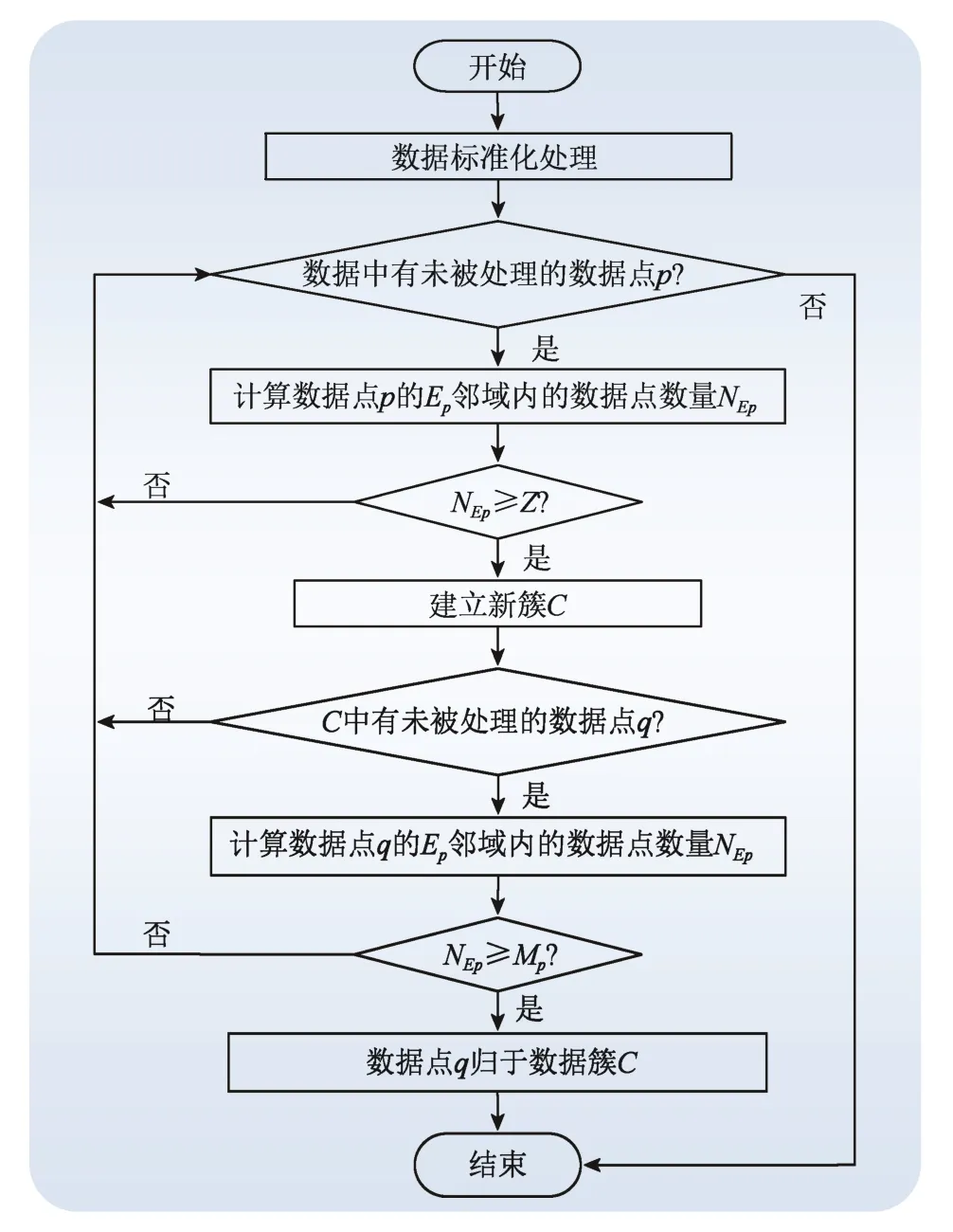
图4 基本DBSCAN算法流程图 Fig. 4 Basic DBSCAN algorithm flow chart

本文对基本的聚类算法进行改进：结合初始数据特性，对上述2个重要参数进行自动选择，以确保聚类结果的正确性。

改进的DBSCAN聚类算法主要的处理步骤为：

（1）根据初始数据量的大小，规定噪声点的可接受占比σ。假定σ=2%；初始变化量k=2。

（2）令Mp=k。计算每个数据和其第k个最近对象间的距离d。初始数据中，所有的对象集合记为Dk。将Dk中累计概率位于6%～94%的数据记 为新的集合，以的数学期望作为Epk：

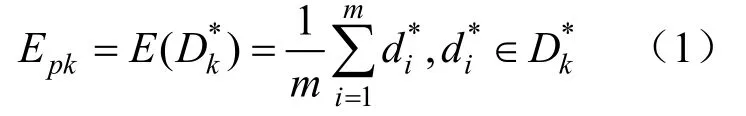
（3）统计初始数据里所有元素Epk邻域内点的个数，其数目集合记为Pk。同上，将累计概率 在6%～94%范围内的元素记为集合，将的数 学期望重新赋值给Mpk。

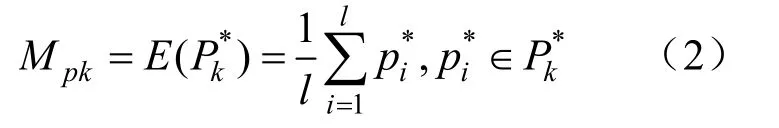
（4）以对初始数据进行处理，并由聚类结果计算噪声数据占比Rk。

（5）若k＞2，且|Rk-1-Rk|≤σ，则Mp=Mpk，Ep=Epk，流程结束；否则，令k=k+1，重复上述步骤。

选取“风速-功率”“风速-桨距角”等变量进行聚类，结果如图5所示。

图5 基于改进DBSCAN算法聚类结果 Fig. 5 Clustering results based on improved DBSCAN algorithm

除此之外，风电机组性能在一定程度上会受到空气密度、风速等因素的干扰，因此需要考虑减小或消除此类因素的影响。

空气密度和风速标准化处理过程如下：

式中：ρ为空气密度；B为气压；R为气体常数，设置为287 J/(kg·K)；T为环境温度；vn为标准空 气密度下的风速；v为实际风速；0ρ为标准大气 压下的空气密度，取1.225 kg/m3。

经过数据预处理后的“风速-功率-桨距角”三维特性散点图如图6所示。

图6 预处理后三维特性散点图 Fig. 6 Three dimensional characteristic scatter diagram after pretreatment

通过对比图3、图6可以看出，本文所采用改进的DBSCAN算法可以有效剔除异常数据。清洗掉的异常值占45.3%。

2.2 基于最小二乘法机组特性曲面拟合

为了减小离散采样数据误差，需要对三维特性散点图进行拟合处理。

最小二乘法是一种广泛被用来解决曲线曲面拟合问题的方法[8]。使用该方法可避免相邻分段上的特性曲线不连续不平滑的问题，非常适合于数据量大且形状复杂的离散数据拟合[9]。

最小二乘法拟合函数多项式可表示为：

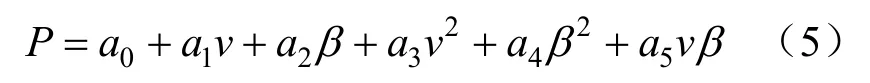
式中：P为风电机组输出功率；v为风速；β为桨距角；aj即为拟合曲面的一组系数。

为了得到不同平均风速下风电机组最优桨距角，需要求解上述拟合函数。通常求解非线性方程的方法有梯度法和牛顿法。

梯度法的缺点是收敛速度慢，其迭代方程为：

式中：α为迭代步长；-gk表示负梯度方向。

牛顿法又称海森矩阵法，其迭代方程为：

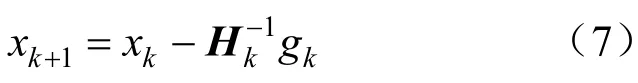
式中：Hk为海森矩阵。

与梯度法相比，牛顿法保留了泰勒级数的一阶项且利用了二阶项、考虑了梯度变化趋势，其优点是搜索方向更好、收敛速度快，缺点是因需要计算海森矩阵及其逆矩阵，所以其计算量大。

用雅可比矩阵近似代替海森矩阵，高斯-牛顿法很好地解决了这一问题。

考虑当海森矩阵为不满秩矩阵时则无法进行迭代，故需引入一个单位矩阵：

将式（9）代入式（7），从而得到LM算法的迭代格式：

式中：μ表示阻尼因子，为正值。

LM算法解决了海森矩阵不满秩无法迭代的问题，且具有梯度法和牛顿法的优点。故本文采用LM算法求解拟合函数。

通过LM算法求解出在问题域上全部节点的系数，即可得到三维特性曲面拟合关系式：

“风速-功率-桨距角”三维特性曲面拟合结果如图7所示。

对于新式风电机组，最优桨距角的角度除0°外，还可以调节为正角度或负角度。本文以1 m/s为步长，在不同平均风速下对基于最小二乘法拟合的曲面进行切割，对切割形成的曲线求功率最大值对应的桨距角。最终得到的不同平均风速下风电机组最优桨距角如表1所示。

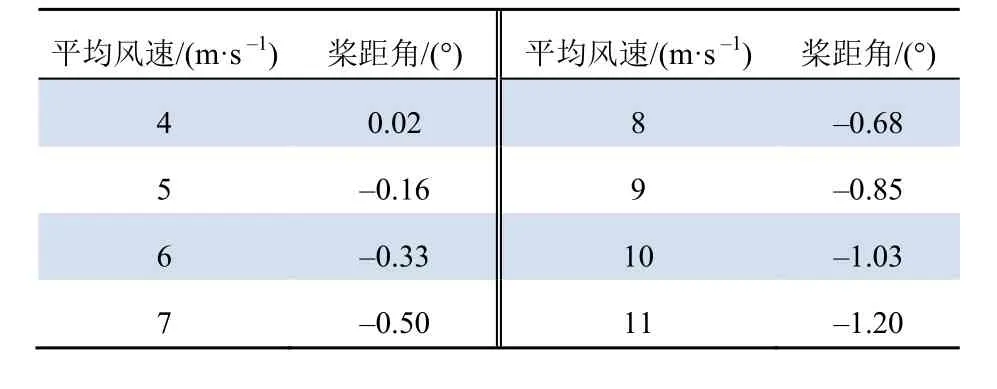
表1 不同平均风速下风电机组最优桨距角 Tab. 1 Optimal pitch angle of wind turbine under different average wind speeds

3 算例验证

本文以某5 MW风电机组为对象在Bladed进行建模。机组主要技术参数如表2所示。

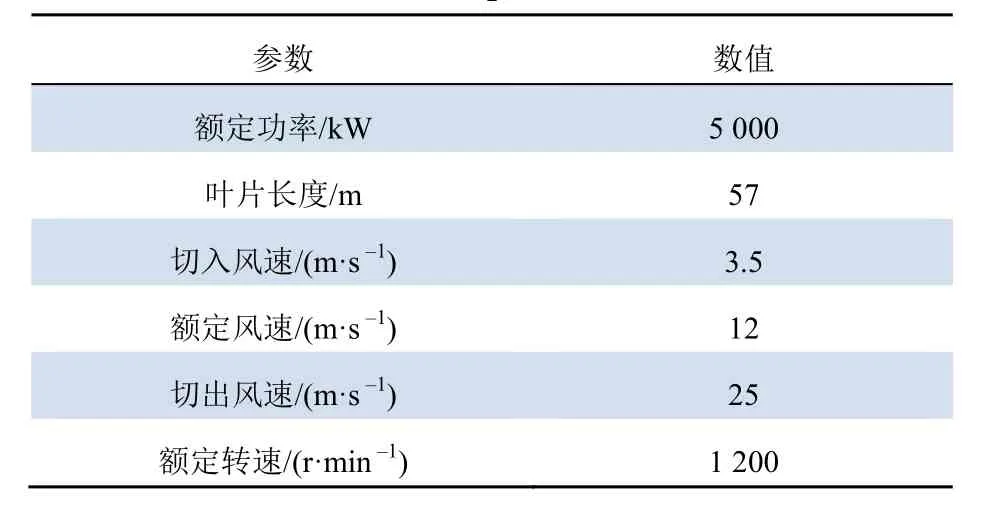
表2 仿真机组主要技术参数 Tab. 2 Main technical parameters of 5MW unit

仿真计算中，为模拟实际风况，湍流风平均风速设置为4 m/s、6 m/s、8 m/s、10 m/s、12m/s。

为了模拟实际风电机组最优桨距角误差情况，设置：最优桨距角最大值为5°，最小值为-5°；每0.5°为1种工况条件，其中风电机组理论桨距角为0.5°，故最优桨距角工况共21种；每个工况时长600 s；每1 s输出一条数据，共输出数据61 950条数据。

输出量包括风速、功率、桨距角、发电机转速以及转矩。

仿真中出现的机组运行异常或提前终止均不做处理，以此验证本文所提方法的实用性。

首先，将桨距角数值设置为理论桨距角，仿真运行得到风电机组输出功率；然后计算得到机组发电量，视为“初始发电量”；同理，最优桨距角仿真运行得到的发电量视为“修正后发电量”。

桨距角修正前后风电机组1 h的发电量总体情况如图8所示，具体数据如表3所示。

图8 Bladed中桨距角修正前后发电量对比图 Fig. 8 Comparison of power generation before and after pitch angle correction in bladed

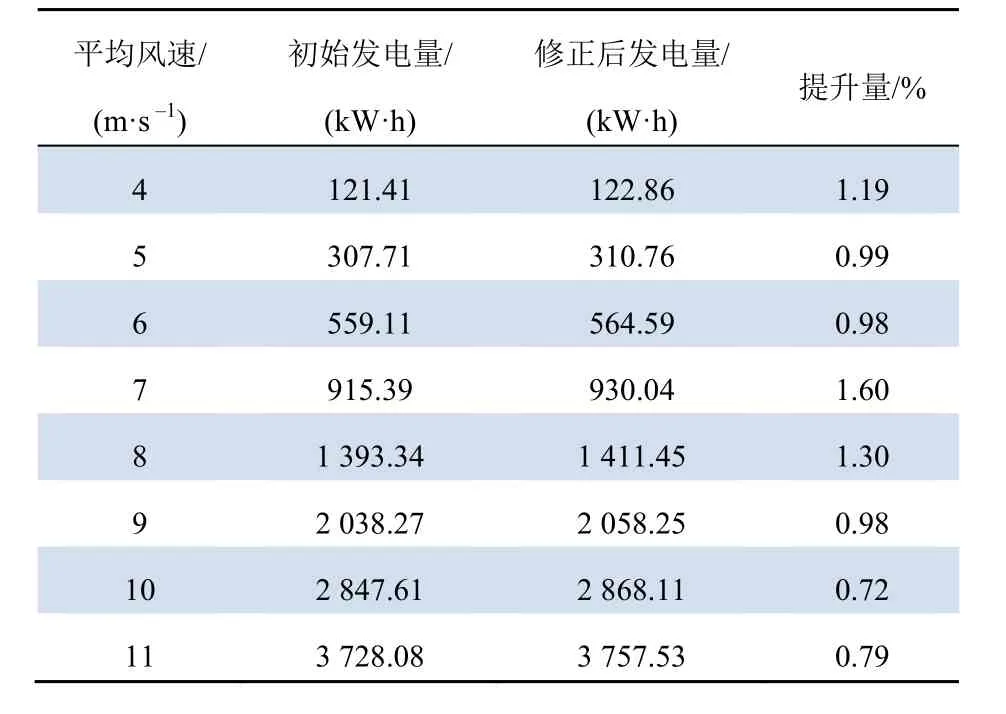
表3 Bladed中桨距角修正前后发电量具体数据 Tab. 3 Data of power generation before and after pitch angle correction in bladed

由表3及图8可知，当平均风速在额定风速以下时，通过本文提出的辨识方法求解得到的最优桨距角能够在一定程度上提升风电机组发电量。平均风速为7 m/s时，发电量提升最为明显——相较于修改前提升了1.60%。当平均风速临近额定风速时，发电量的提升量较低。

将机组模型提取到MATLAB中，在MATLAB环境下进一步验证该最优桨距角的有效性。针对风电机组的强非线性，为获得其线性化数学模型，考虑所需要的输入、输出以及模态。采用泰勒级数在各风速点进行线性化展开，可以获得如式（12）所示风电机组多输入多输出状态空间方程。

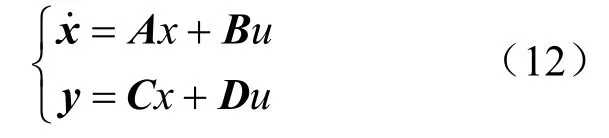
式中：A、B、C、D表示三维系数矩阵；x表示状态变量；u表示输入变量；y表示输出变量。

提取到模型后，在相同的工况下再次进行发电量提升验证。桨距角修正前后机组1 h的发电量情况如图9所示，具体数据如表4所示。

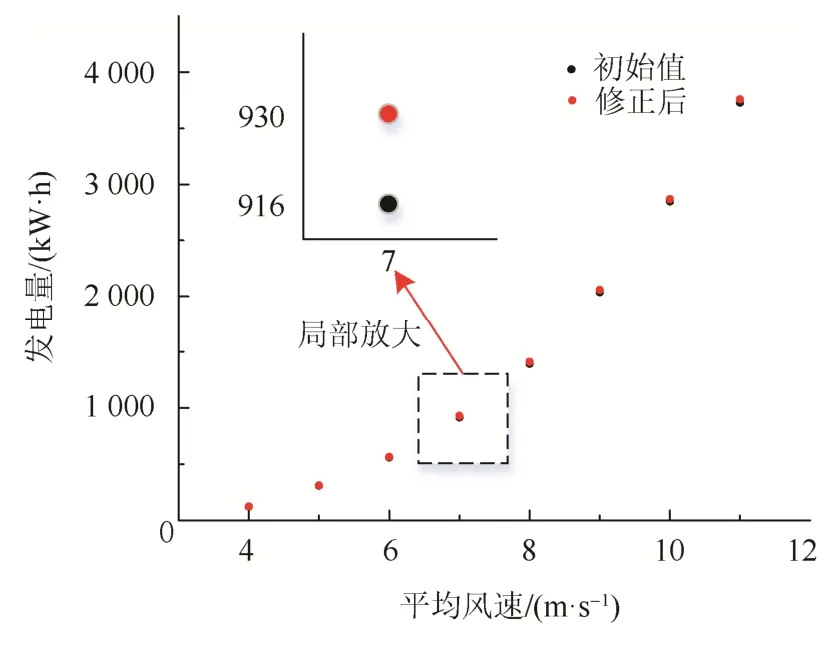
图9 MATLAB中桨距角修正前后发电量对比图 Fig. 9 Comparison of power generation before and after pitch angle correction in MATLAB

表4 MATLAB中桨距角修正前后发电量具体数据 Tab. 4 Data of power generation before and after pitch angle correction in MATLAB

由表4及图9可知，在MATLAB仿真实验中，辨识得到的最优桨距角能够提升风电机组发电量。在平均风速7 m/s的湍流风工况下，发电量提升最为明显——相较于修改前提升了1.59%。当平均风速临近额定风速时，发电量的提升量一般，平均风速10 m/s的湍流风工况下提升量为0.70%。

上述2种模型的计算结果均表明，在相同的工况下，最优桨距角可提升风电机组发电量，且提升量几乎一致；这说明本文提出的最优桨距角策略具有有效性。

4 结论

针对风电机组最优桨距角与理论桨距角不一致的问题，本文提出了一种基于运行数据驱动的最优桨距角辨识方法。对同一参数的机组，将辨识得到的最优桨距角分别通过Bladed和MATLAB进行验证。通过算例验证分析可以获得以下结论。

（1）针对算例验证中5 MW风电机组，通过本文方法可获得不同平均风速下最优桨距角。当平均风速在额定风速以下时，桨距角修正后能够在一定程度上提升风电机组发电量。在平均风速7 m/s的湍流风工况下，发电量提升最为明显：相较于修改前提升1.59%～1.60%。

（2）在Bladed和MATLAB模型验证中，桨距角修正后机组发电量的提升基本一致，故该辨识方法所获得的最优桨距角具有有效性。

本文所提出的风电机组最优桨距角辨识方法依赖于风电机组运行数据。当风电机组模型参数发生改变时，本文结论中的数据不再适用。

基于此不足，进一步研究方向为：考虑不同的风电机组模型，验证风电机组最优桨距角辨识方法的普遍性。