流化床制粒过程颗粒水分预测研究
2020-06-15李民东王海燕陈庆伟周军皇攀凌
李民东,王海燕,陈庆伟,周军,皇攀凌
(1.山东大学 机械工程学院,山东 济南 250061;2.山东大学 药学院,山东 济南 250012;3.山东大学 高效洁净机械制造教育部重点实验室,山东 济南 250061)
流化床的工艺参数少,操作时间短,并且可以减低操作者的劳动强度,因此广泛应用于药物制粒的生产过程中[1]。
水分是流化床制粒过程中颗粒的关键质量属性之一,水分含量影响最终产品的流动性、可压缩性和稳定性[2]。许多学者已经对流化床制粒过程水分预测方面做了相关研究,Rantanen等[3]采用近红外水分测量与温湿度测量相结合的方法,控制颗粒水分含量的变化。Barla等[4]采用近红外技术,利用PLS对流化床制粒过程中颗粒的水分进行了定性和定量分析。提升对流化床制粒过程中水分的预测精度,使得水分含量保持在一定范围内,对提高制粒的成功率具有重要意义。
现阶段的流化床制粒过程中无法对物料的关键质量属性进行科学准确的分析,只能在制造生产过程中不断取样,依靠工厂工人的经验对制粒过程颗粒的质量属性进行分析。这样使得流化床制粒效率低下,而且很难达到批次间的一致性。为了实时掌握颗粒的关键质量属性,从而对流化床的工艺参数进行及时的控制,必须对流化床设备进行工程化改造。
1 实验部分
1.1 试剂与仪器
微晶纤维、玉米淀粉、乳糖、羧钾淀粉、对乙酰氨基酚均为分析纯。
LGL 002实验型流化床;xy-102水分含量测试仪;MicroNIR PATU微型近红外光谱仪。
1.2 设备改造
流化床设备改造示意图见图1。

图1 流化床设备改造示意图Fig.1 Schematic diagram of fluidized bedequipment renovation
在流化床的底锅上进行打孔,用于放置近红外探头,孔的位置与物料取样口在同一水平线上,这样可以保证近红外光谱数据和获得的一级数据在相同或相似条件下获得。采用法兰将外接探头安装到流化床内部使流化床的探头长度为大概6 cm。
1.3 制粒
活性药物成分、微晶纤维素、玉米淀粉、乳糖、羧钾淀粉按比例混合,采用顶喷方式的流化床进行制粒。从流化床取样口取出少量待测样品,放到重为M的瓶中称重,测得重量M1,进行近红外光谱采集。样品烘干,每隔1 h称量1次,直到样品重量不再变化,经过大约6 h测得烘干样品重量为M2,通过计算烘干前后的M1和M2质量差,求出样品的水分含量[5]。

实验过程中每一批次隔3 min取1次样品,每批15个样品,采集了6批一共90个样品。其中第一批样品中水分含量见表1。从所有样本中随机选取60个样品作为测试集,用于建立模型并进行交叉验证,剩下的30个样品作为预测集。
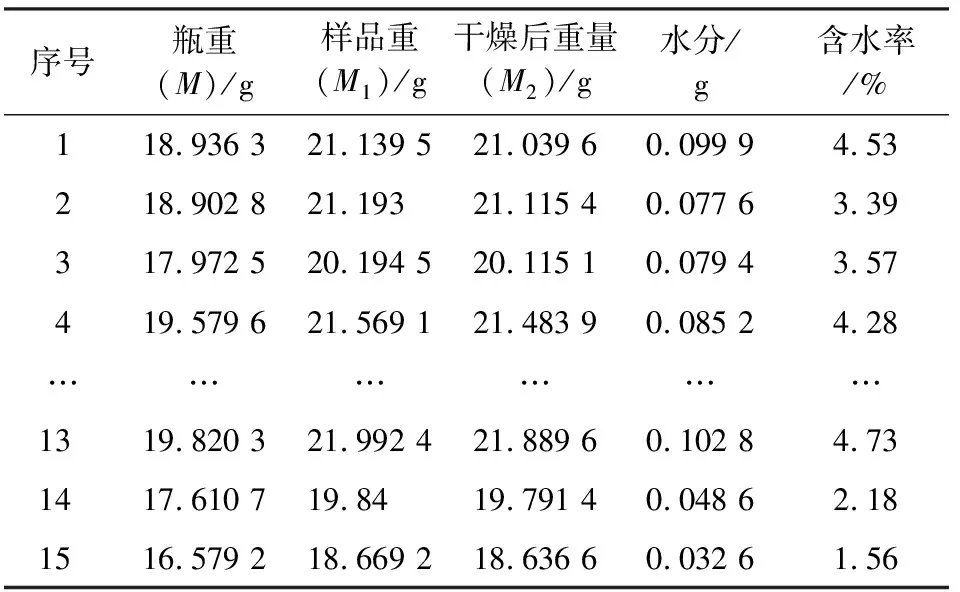
表1 第一批样品中水分含量Table 1 Water content in the first batch of samples
1.4 光谱采集
近红外光谱仪采用漫反射方式采集样品光谱,光谱范围是908.1~1 676.2 cm-1,波数间隔为6.195 cm-1,共有125个点的光谱数据 光谱采集软件为MicroNIR Pro v2.3,得到样品的近红外光谱图见图2。

图2 近红外光谱数据图Fig.2 Near infrared spectroscopy data map
1.5 光谱建模
为了研究对比建立近红外光谱预测的最优模型,采用全光谱进行建模分析。分别采用偏最小二乘法(PLS),粒子群-岭回归(PSO-KRR),随机森林-偏最小二乘法(RF-PLS)建立回归模型。通过计算预测集的均方根误差(RMSE)和相关系数(R)作为模型的评估标准,RMSE越小,R越接近于1,说明真实值与预测值之间的误差越小,模型的预测能力越好。
2 结果与讨论
2.1 偏最小二乘法(PLS)
PLS[6]是一种基于因子分析的多元线性回归方法。近红外光谱数据维度较多,而且各个维度之间都存在多重相关性,传统的回归分析预测效果较差。PLS集中了主成分分析、典型相关分析和多元线性回归的特点。在进行PLS计算前,光谱数据和浓度数据都经过中心化处理,对光谱矩阵进行分解提取主因子,消除光谱矩阵中无用的信息,保证光谱数据和水分浓度之间具有良好的线性关系。
首先采用全光谱PLS进行建模,用不同的主成分数在测试集上进行十折交叉验证,取10次得到的RMSE的平均值作为评价标准,当交叉验证均方根误差(RMSECV)最小时,对应的主成分数即为最优。用不同的主成分建立的模型的RMSE见图3。

图3 主成分数与RMSE的关系Fig.3 Relation between the number of principalcomponent and RMSE
由图3可知,当主成分的数目为13时,验证集的RMSECV值最小。因此,选用主成分为13对预测集进行建模。得到预测集的RMSE值为 0.218 0,相关系数R为0.971 7,结果见图4。
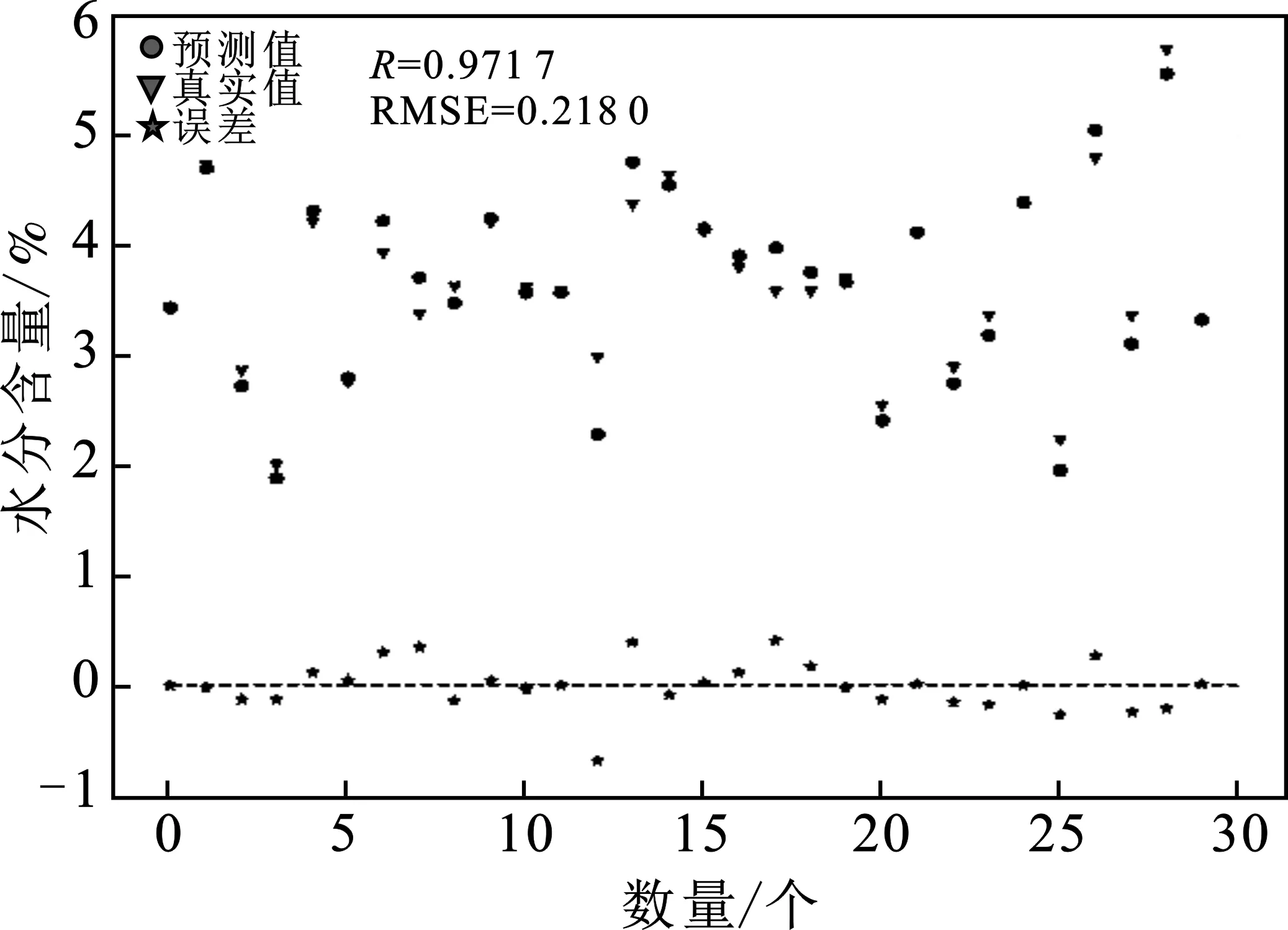
图4 PLS模型预测集水分含量预测Fig.4 Prediction of catchment watercontent by PLS model
2.2 粒子群-核岭回归(PSO-KRR)
岭回归[7]是一种有偏的回归估计方法,实际上使一种经过优化的最小二乘算法,可以用于克服光谱数据多重共线性的问题。将光谱数据进行l2正则化处理,损失一部分光谱信息,可以有效防止模型的过拟合,从而获得更符合实际、更加可靠的回归系数。
核岭回归[8]是一种将自变量数据进行非线性变换再进行岭回归的技术。基本原理是将原始数据通过核函数映射到高维空间,并用得到的新的高维空间数据建立岭回归模型。原始的数据大多是非线性的,而映射后的数据在高维空间往往会呈现出线性的关系,选择合适的核函数,将光谱数据映射到高维空间进行建模,这样得到的模型会有更高的精度和更强的泛化能力。
粒子群优化算法(PSO)[9]是一种基于种群的随机优化算法,使用粒子来模拟鸟群中鸟的捕食,通过判断与目标点的距离来寻找全局最优点。PSO算法初始化一群随机粒子作为随机解,以KRR模型预测的均方根误差RMSE作为适应度函数来评价解的品质,通过迭代搜寻最优解即得RMSE最小。算法的建模流程图见图5。

图5 PSO-KRR建模流程图Fig.5 Modeling flow chart of PSO-KRR
通过PSO优化算法,选择KRR中的最优参数正则化系数alpha,粒子群数目选择50,目标参数的范围在1×10-9~1×10-5之间,更新的最小速度为1×10-9,获得的最优解为alpha=7.681 010 79×10-6,将最优解带入KRR模型中,得到预测集RMSE为0.215 4,相关系数为0.973 8,结果见图6。

图6 PSO-KRR模型预测集水分预测Fig.6 Prediction of catchment water by PSO-KRR model
2.3 随机森林-偏最小二乘法(RF-PLS)
近红外光谱仪数据采集过程中,不可避免的会有一些干扰因素,就会产生一些对预测结果无效甚至起反作用的光谱数据,影响模型的预测结果。进行对近红外光谱数据的波段选择,剔除无用的光谱数据,不仅可以降低数据的维度,还可以提高预测的精度[10]。
随机森林(RF)是一种回归分类器,使用多个决策树来训练样本,并集成预测。从原始的数据中随机选取一部分特征进行组合,然后对每个特征组合进行打分。用变量重要性的二次距离确定变量重要性的最小阈值,利用所选变量的最优子集进行预测[11]。对于含有噪声及缺失值的数据,采用RF建模会得到较为准确的结果,对每一个维度的特征进行特征权重提取,设置权重阈值0.005,对贡献度小的无用数据进行剔除,得到最优的特征组合共有47个维度,基本遍布整个光谱的各个阶段,见图7。

图7 随机森林进行波段选择Fig.7 Feature selection by random forest
利用RF选择出来的波段,用PLS进行建模,遍历主成分数,交叉验证,得到最优主成分数为12,将主成分数带入PLS模型中,得到预测集RMSE为0.205 9,相关系数为0.973 3,结果见图8。
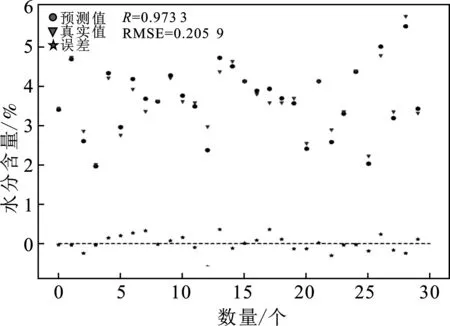
图8 RF-PLS模型预测集水分预测Fig.8 Prediction of catchment water by RF-PLS model
通过上述建模,PLS、PSO-KRR、RF-PLS建立的模型的均方根误差,相关系数见表2。

表2 模型的RMSE和RTable 2 RMSE and R of models
3 结论
PLS模型的RMSE为0.218 0,R为0.971 7,PSO-KRR模型的RMSE为0.215 4,R为0.973 8;RF-PLS模型的RMSE为0.205 9,R为0.973 3,模型的RMSE得到了较大的提升。预测精度更高,为流化床制粒过程颗粒质量属性的数字化、智能化监控提供方法。
