巧用技术 优化课堂
——以《圆的面积》教学为例
2020-06-15贺慧杰
贺慧杰
【教学内容】
浙教版六年级上册第68~70页。
【教学过程】
一、导入新课,揭示课题
(出示两个大小略不相同的圆)
师:这两个圆哪个大?哪个小?
生:左边的大一点,右边的小一点。
师:你是怎样比较的?
生:认真观察,就知道谁大谁小了。
师: 这两个圆的大小相差了多少?
师:有点困难,要想知道它们的大小、相差多少,就必须知道它们精确的面积。这节课我们就来研究圆的面积。
【设计意图:本环节采用直接引入方式激发学生的学习兴趣,通过问题引领,让学生一步步深入思考,让学生感受到仅仅靠肉眼判断哪个圆大,哪个圆小只是初步认识,还要知道它们精确的面积,进而启发学生进一步探索的欲望。】
二、探究新知
1.讨论“转化”的策略。
师:在探究之前,我们先来回忆一下我们之前学过哪些图形的面积计算公式?这些计算公式是怎样推导的?推导过程有什么共同点?
生:我们通过割补的方法,把不会计算面积的图形转化成我们会计算面积的图形。
师:化未知为已知!这是我们在学习数学的过程当中一种很重要的方法。
师:那圆的面积我们该如何去求呢?
【设计意图:本环节通过回顾总结平行四边形、三角形、梯形面积公式的推导体验转化思想,感受转化思想在数学学习中的重要性,同时为学生接下来圆的面积公式的探索做铺垫。】
2.尝试“转化”。
(1)微课教学。
师:今天我们可不可以用转化的方法来推导出圆的面积计算公式呢?
师:请同学们先看一下导学案上的前三个问题,带着问题,来看一段微课!

播放微课:

【设计意图:本环节中学生带着问题,通过微课进行圆的面积概念学习,经历把圆分成4 份、8份、16 份、32 份、64 份……同时结合动画的形式使比较抽象的知识更加直观化,让学生直观地看到圆的面积转化为平行四边形面积的过程,更直观地提升学生对转化思维的感悟,并再次感受极限思想;这一环节利用3 分钟的时间把概念教学讲清楚,为下一环节节省出大量的时间,让学生自主探索。】
3.学生合作探究,推导公式。
(1)讨论探究,出示引导语。
师:我们一起交流一下刚才导学案的三个问题。
生:圆转化成了平行四边形。
生:原来的图形与所拼图形之间形状变了,面积没变。
生:转化后平行四边形的底相当于圆的半个周长,高相当于圆的半径。
(2)演示公式推导过程。
师:根据已知条件,谁来试着推导一下圆的面积公式?
师:请大家尝试用“因为……根据……所以……”类似的关联词和同桌说一说刚才我们推导圆面积公式的过程。(学生自己说,如果觉得有困难可以求助2 号iPad)
【设计意图:本环节中在观看好微课后,结合导学案上的问题,在教师的引导下推导出圆的面积公式,但本环节还有一个重要任务是让学生在关联词的辅助下有理有据地说一说圆的面积公式推导过程,促进学生数学表达能力的发展,提升学生核心素养。】
4.小组论证圆的面积公式。
师:刚才我们一起通过平行四边形推导出圆的面积公式,现在请同学们自己动手把平均分成16 等份的圆,拼成其他可以计算面积的图形。
(1)活动要求。
①在iBooks 上将一个16 等分的圆转化成学过面积的平面图形。
②想一想,这个图形的底和高与圆有什么关系。
③自己试着推导出圆的面积计算公式。
(2)学生交流、汇报。
师:第二组先来,你们是把圆形转化成什么图形来研究的?
生:我们是转化成平行四边形,不过跟刚才那位同学不一样。
师:哪里不一样?
生:刚才那位同学是一层的平行四边形,我们小组把16 等分的圆可以转化成平行四边形的剩余情况都找出来了。
(小组投屏展示)

师:请你们小组来汇报一下你们是怎么研究的。
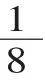
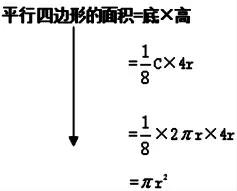
师:选择其他转化方法的小组你们是怎样推导的?
生:把圆转化为三角形。

生:把圆转换为梯形。

(3)思路拓展。
师:大家真了不起,用了这么多方法来推导圆面积的计算公式。
师:昨天2 班的一个小组是这样推导的,你估计他们组是将圆转化成了什么图形来研究的?
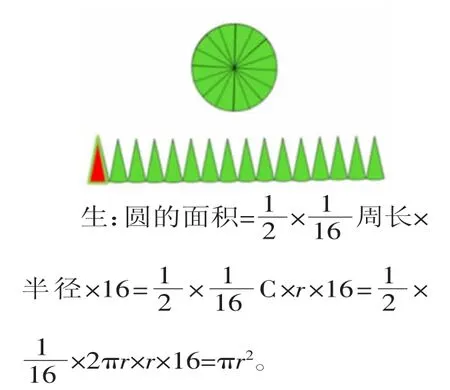
师:你的抽象思维非常棒!
5.小结。
师:通过上述一系列的操作和推算,我们都得到了圆的面积是πr2,也就是说,要求圆的面积是多少,必须知道圆的半径。
【设计意图:本环节在前面的铺垫中启发学生自主探究,把16等分的圆拼割成不同的已知的图形再推导出圆的面积。本环节主要运用iPad 自带软件iBooks 让学生自主操作,完成拼割,为课堂节省时间,提高效率,同时提高组拼的精确度减少误差。这一环节在设计时也用到了同屏技术,学生可以通过苹果TV 等把自己的操作过程投放到大屏幕上,展示一方面激发学生的兴趣,另一方面起到启发没有思路的学生想出自己的方法。】
三、巩固深化知识(UMU 平台)
基础练习:笔筒的底面是一个直径为6 厘米的圆形,把它放在桌上,会占去多少面积?
A.18.84B.28.26
C.9.42D.37.68
提高练习:图中的圆半径是1米,求:正方形和圆之间阴影部分的面积?(精确到小数点后两位)

能力提升:图中的圆半径是1 米,求:正方形和圆之间阴影部分的面积?(精确到小数点后两位)

四、课堂小结
师:今天我们一起研究了什么问题?我们是怎么研究的?
师:同学们有没有发现这些方法都用到了转化的思想,一开始求平行四边形,我们把它转化成什么图形?求三角形我们转化成?梯形呢?圆呢?
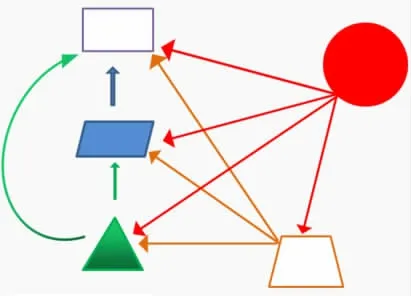
【设计意图:拓展学生的思维方式,原来我们可以从很多个角度去观察解决问题。同时对小学阶段的面积推导方法进行总结,让学生再次感悟转化思想在数学中的应用。】
