“三问”凸显数学本质——听特级教师罗鸣亮教学有感

刘 萍

我们在教学时经常做这样的思考：自己的教学体现出数学的本质了吗？如何才能很好地体现相关内容的数学本质？让我们走进特级教师罗鸣亮的课堂，一同领略“明师之道”精神指引下的凸显数学本质的教学精彩，一起探索学习精彩背后给我们带来的无限思考与启发：究竟罗老师是怎样把握数学本质？又是在哪些环节中让本质得以凸显，真正做到学生的学习乐在其中，悟在心中！

一、在质疑中，“探问”数学本质

“你知道吗？”是人教版小学数学教材中，作为拓展知识的一个板块，罗老师设计执教了《2、3、5 倍数的特征》一课。他的设计直奔主题，引导学生质疑提出问题，在疑问探究中彰显数学本质。

师：我们已经学过了2、3、5的倍数的特征，怎么判断一个数是不是5 的倍数？

生：看它的个位上是不是0或5。

师：怎么判断一个数是不是3 的倍数？

生：将所有数位上的数字相加，看看是不是3 的倍数。

师：5 的倍数只看个位数，3的倍数要看各位上数的和，有困惑或新的问题吗？

生：为什么5 的倍数只要看个位就行，而3 的倍数要看各位上数的和呢？

师：这个问题提得好吗？好在哪儿？

生：他把3 和5 的倍数特征做了比较。

师：今天的学习就从你们提出的疑问开始。

【思考：教学中经常会遇到这样的课型，传统做法都是通过举例、观察、归纳得出结论。最后学生就能带着“结论”畅通无阻地进行判断，当多问一句“为什么？”时，学生皆是一脸茫然。而反观罗老师的这一课，我们不难领悟他的用意：数学学习是否就止步于知识的表象？如何让学生透过表象学会质疑、探究、反思，在感受数学学科理性精神的精髓中形成终身受用的数学素养。当我们也本着这样的思考重新审视教材、关注学生、设计教学流程时，课，才真正走向了深入。

启发：“有困惑或新的问题吗？”唤醒学生不知所以然的“为什么”，这样的问题问出需要教师更多的勇气和底气。然而，正是这样朴实的一问，把学生甚至听课教师都推向理性思考：面对朴素的教学内容去思考知识的发生发展过程，去思考这是什么？为什么会是这样？我们可以用什么方法寻找答案？在层层深入的思考中拨开面纱，凸显本质，这样单刀直入的做法非常适合高段学生想当然却不知所以然的学习状态！紧接着罗老师又抛出一个十分精彩的问题：“这个问题提得好吗？好在哪儿？”质疑、探究、反思都在这一问中得以体现，培养学生发现问题数学品质的同时，还引导学生对“问题”的落脚点就其问题本源进行追述，这两个问题看似平常却蕴含大学问，值得借鉴。】

二、在迁移处，“追问”数学本质

罗老师的课跌宕起伏，富于变化，能让学生喜形于色的同时，又顿挫波折。原因在哪？因为他早已将问题的本质了然于心，并擅于顺着学生的认知习惯，把握生成资源，在知识点的迁移处伺机追问，问中讲理，辩中明理，以达探清数学本质的目的。

《分数乘法》精彩片断回放：

师：我也来举个例子，20×3，怎么算出来的？

生：2×3 等于6，就是有2 个10 乘3，有6 个10，就是60。

师：有道理，谁来说0.2×3？

生：2 个0.1 乘3，就是6 个0.1，就是0.6。

师：是的，计算计算就是在计一计、算一算有多少个计数单位。

【思考：这是《分数乘法》课中的一个环节，罗老师根据学生算法了然，算理懵懂的学情设计一个个问题，层层迁移，在追问中沟通算理本质。首先，他借助已有经验20×3 是怎么算出来的，引导迁移0.2×3，再迁出×3。在学生的自主迁移过程中不断追问“怎么算的？”从而明晰整数乘法、小数乘法、分数乘法算法的连通性，最后借数形结合，水到渠成地道出最为精辟的一句话：“计算计算就是在计一计、算一算有多少个计数单位”，让听课教师赞叹不已！

启发：什么样的课可以这样上？同一领域的课题，因为有共性，不论是上述算理的共性，还是如图形领域方法策略上的通用，亦或是统计领域中数据分析能力的培养，都可以借助“迁移”对数学本质进行沟通和彰显，都需要我们向罗老师学习：横比不同版本教材，纵比不同学段体系，捋清知识之间的内在联系，明晰结构，认清本质的求实做法，才能挖掘知识内涵，上出简而不凡的课。】

三、在出错后，“辩问”数学本质

罗老师上课很幽默、轻松，他会设计各种包袱，挖各种坑，让学生往里跳，让学生处在出错后不思考难受、不说理难过的愤悱状态。

《长方形面积》精彩片断回放：

师：信封里还有个长方形，谁猜对了它的面积，就送给谁。这个长方形每行有4 个正方形，有2行，谁知道它的面积？

生：8 平方厘米。

生：我认为还有可能是8 平方分米，不可能是8 平方米。

生：还可能是8 平方毫米，甚至更小。

生：8，这个数字是确定的。

师：（出示图形）你说对了吗？

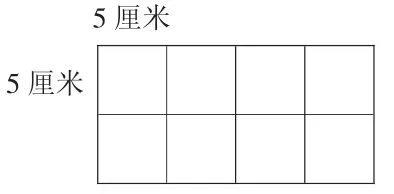
生：唉，没有！

师：错在哪儿了？

生：小正方形的边长不是1厘米。

师：谁的错？

生：你的错! 是你没讲清楚。

师：那我该怎么描述，让大家不犯错？

生：要这样说：正方形的边长是5 厘米，每行有4 个，有2 行。

师：现在可以算出长方形的面积了吗？是多少？

生：200 平方厘米。

师：如果按你们之前想的，正方形的边长是1 厘米，每行摆几个？摆几行？需要多少个正方形？

生：摆10 行，每行摆20 个，需要200 个。

师：为什么也是200？

生：因为边长5 厘米的正方形摆出的长方形，实际上就是边长1 厘米的小正方形摆出的长20 厘米，宽10 厘米的长方形。

小结：是的，不论正方形的边长是多少，最终都要计算出一共有多少个这样的单位面积。

师：都是200 平方厘米，你会选哪一种摆法？

生：第二种，快，省时间。

生：不一定，要看实际情况，要看这200 平方厘米摆在什么地方……

【思考：之前罗老师都是用“单位面积”的小正方形，借格子图让学生自主探索领悟长方形的面积本质：长×宽。但他的课并不是一味地给学生留下单纯的一种模式或者一种思维，通过让学生猜想200 平方厘米的长方形，突破了“单位面积”的思维定势，让学生在错误中辨析联系，促进对面积公式本质意义的深入理解。

启发：巧用“错误资源”是反思性学习的载体，猜测错因，提出纠错方法，让学生当小老师，在反思中对话，在对话中辨析面积的本质内涵，达到内化知识的目的。显然，这些“错误”都是罗老师有心的预设。怎样像罗老师一样预设“错误”，便是我们要学习之处。可以在学生的思维定势处预埋“地雷”，可以从课后练习中（特别是星号题）挖掘素材，还可以借课的延伸性前置知识点，造成已学知识“无用”的“错误”。还要营造“主体氛围”（当小老师），让学生错的理直气壮，让学生说得斗志昂扬！培养学生大胆探索、敢于质疑、独立思考的精神，做到不唯师、不唯书，学会讲道理。】