锥台点阵异面压缩仿真建模方法的比较研究
2020-06-03孙彦彬徐天时马思群
孙彦彬,徐天时,马思群
(大连交通大学机车车辆工程学院,辽宁 大连 116028)
点阵材料是由特定的胞元在空间中有序排列构成的组合结构材料[1]。依据胞元的类型,点阵材料主要分为四棱锥点阵、金字塔点阵、Kagome点阵、编织结构点阵等[2]。点阵材料具有优异的力学性能、复杂的空间结构和多样化的可设计性,近年来被越来越多地关注和研究[3-6]。
点阵材料胞元的尺寸小,在利用仿真方法研究点阵材料性能时,为了体现出点阵的结构特征,往往需要进行精细的仿真建模。韩福娥等[7]在对多级金字塔点阵结构进行压缩吸能研究时,用实体单元对细致的金字塔点阵棱柱结构和面板进行建模,由于二级金字塔结构较复杂,因此采用对称建模的方式以4个金字塔胞元代表整个金字塔夹芯板来进行点阵结构的研究。朱凌雪等[8]在研究芯体截面梯度变化的金字塔点阵平压性能时,用实体单元模拟了芯体,由于模型中最小网格尺寸小于1.5 mm,为了控制仿真模型规模,因此模型中只有一个胞元。考察点阵结构宏观力学性能时,需要点阵胞元达到一定的数量,如果此时仍将点阵结构的细节表达出来,将导致整个模型求解难度增加,这时点阵的细节特征需要进一步简化。徐建新等[9]对金字塔点阵结构进行了低速冲击有限元仿真,在建模时将结构用壳单元和实体单元网格准确地表达出来,在172 mm×172 mm的区域内网格单元数量有近30万个,尽管模型精度足够高,然而这种建模方式并不适合在大型结构中使用;舒剑[10]在对金字塔点阵夹芯结构进行抗暴抗侵彻仿真时,用梁单元简化金字塔结构,与精细模型相比,简化模型的单元数量是原模型单元数量的1/30,但仍具有较高的精度。
建立点阵结构有限元模型时,有必要根据考察的重点忽略一些细节特征,进行合理的简化。模型网格的尺寸足够小才能体现点阵胞元的变形特征,但是工程上将点阵结构应用于整车碰撞安全仿真时,关注的重点是整个点阵块体的力学性能,并且当整车中点阵结构的网格尺寸远小于其他部件时,整个模型的求解时间步长会减小,求解时间增加。为了提高求解效率,从点阵材料力学特征一致性角度出发,研究实体单元替换壳单元建模的可行性,具有实际意义。
1 点阵块壳单元建模的异面压缩仿真
1.1 锥台点阵结构简介
锥台点阵材料的胞元是薄壁锥台结构,胞元在空间上周期排列,点阵的层与层之间对称排布,由钎焊连接在一起。锥台小底面的形状为正方形,边长为a,锥台下边缘形状也是正方形,边长为b,锥台高为h,壁厚为t。垂直于锥台小底面的方向是T方向,又称为异面方向,平行于小底面的方向称为共面方向,即L和W方向。锥台点阵块结构如图1所示。
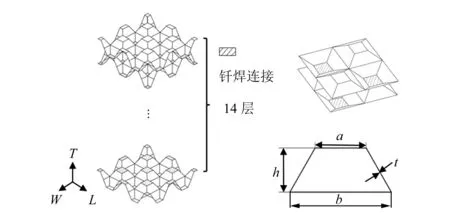
图1 锥台点阵块结构示意图
1.2 点阵块的壳单元建模
以四边形壳单元建立薄壁多层钎焊的点阵块模型。锥台小底面边长a=4.5 mm,锥台下边缘边长b=11.0 mm,锥台高h=6.0 mm,壁厚t=0.8 mm。模型共14层,沿着T方向叠在一起,层与层的间距为0.8 mm,层间以tied单元相连,模拟钎焊连接。整个点阵块的高度是83.2 mm,点阵块在共面方向的整体尺寸是44 mm×44 mm。
点阵块的材料为钢,壳单元属性在PAM-CRASH软件中被赋予可反映各向同性弹塑性的103号材料,表1给出了壳单元的材料参数。

表1 壳单元的材料参数
在T向压缩过程中,点阵层与层之间、点阵块和上下刚性墙之间会发生接触。设定点阵层间的接触方式为36号自接触,接触厚度为0.8 mm,点阵块和上下刚性墙为主从接触,接触厚度为1.0 mm。
图2所示为壳单元点阵块T向压缩模型。点阵块无约束地放在固定的刚性墙上,上端放置一个以1 m/s的固定速度下压的刚性墙,点阵块和上下刚性墙的摩擦系数设定为0.1,这能保证压缩过程中不发生相对滑动。上刚性墙被约束5个自由度,只能在T方向上移动;下刚性墙的6个自由度全部约束住。输出上刚性墙的位移作为压缩行程,上刚性墙的反力作为点阵块的压缩反力。
1.3 点阵块的壳单元建模仿真结果
图3所示是壳单元点阵块模型T方向的压缩力-位移曲线。开始时,主要由4个斜撑的梯形胞元外壁支撑垂向载荷,此时点阵产生的变形主要是弹性变形,在压缩力曲线中,这一阶段的曲线表现为反力随着位移的增大呈直线上升,曲线第一个峰值的力值是触发力。
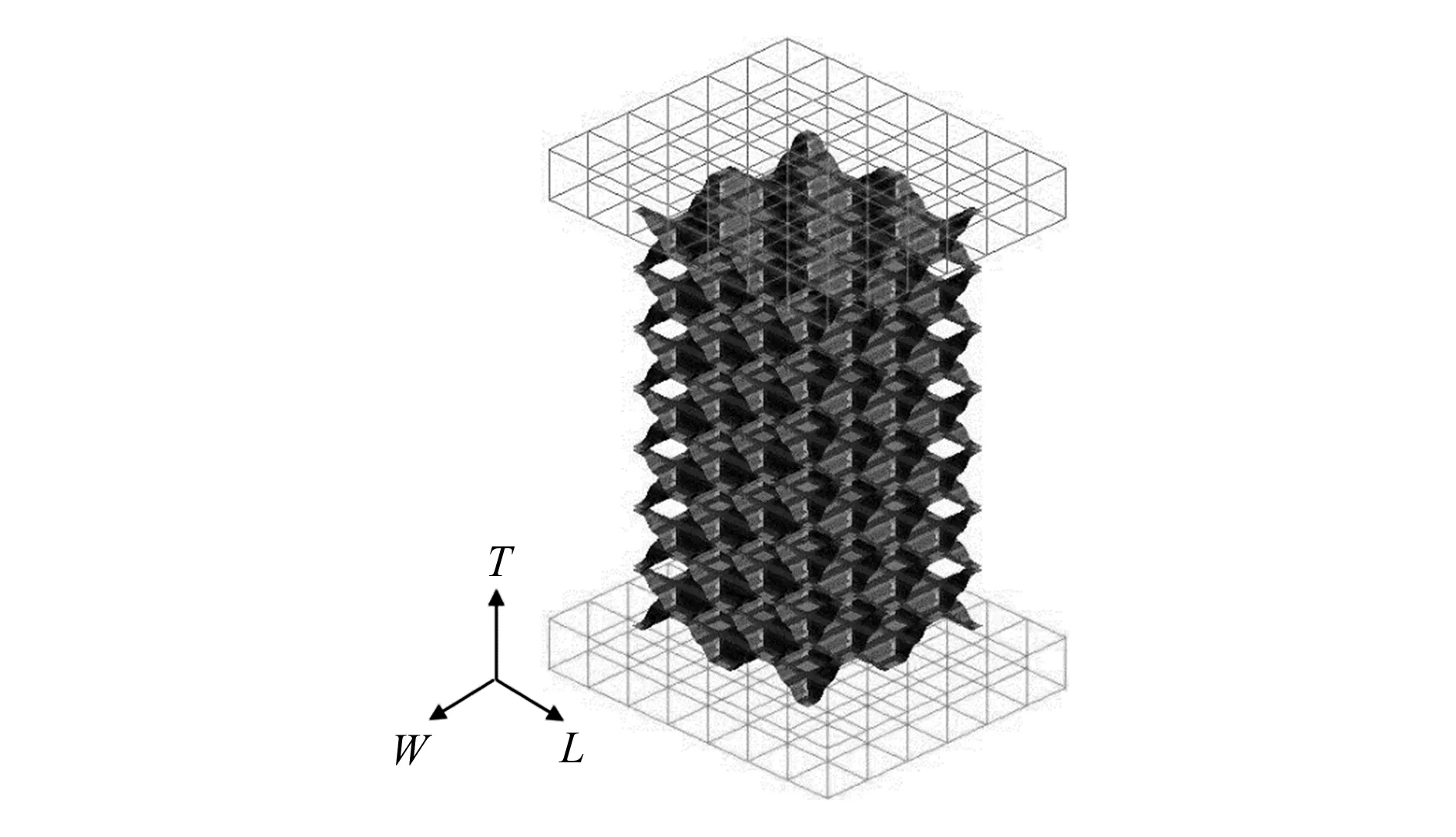
图2 壳单元点阵块T向压缩模型示意图
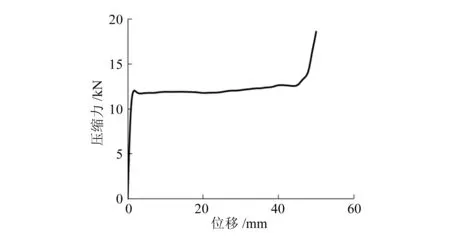
图3 壳单元点阵块T向压缩力-位移曲线
随着刚性墙不断下压,锥台棱边开始产生塑性变形,此时的压缩力曲线呈现出平稳的走势,点阵处于平台力阶段。区别于传统点阵结构,锥台点阵在平台力阶段的力曲线更平稳,没有明显的波动,这是因为在传统结构中,孔壁或杆每折叠一次代表着塑性铰生成一次,相应的力-位移曲线上就产生一次波动,而锥台点阵的塑性铰是锥台的棱边,是预先生成的塑性铰,且塑性铰的数量足够多,因此曲线在平台阶段不产生波动。
最后,当大部分锥台被压平,平台阶段结束进入压实阶段,此时点阵块基本不再产生塑性应变,上刚性墙继续下压导致力曲线陡然升高,开始进入压实阶段时的应变是压实应变。
2 点阵块实体单元建模的异面压缩仿真
2.1 实体单元材料参数
用实体单元建立点阵块模型时,实体单元的属性在PAM-CRASH软件中用41号材料卡片来描述,该材料卡片需要定义一些特征参数。
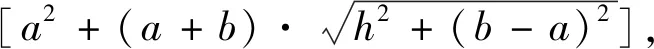
(1)
式中:ρs为基体材料的密度。
式(1)是将点阵绝对理想化后得到的点阵相对密度,实际上锥台棱边的过渡更圆滑,薄壁结构也绝对不是完全平整的,因此结合壳单元模型,给出点阵相对密度的修正系数,修正后的点阵相对密度为:
(2)
式中:S为修正系数,在本文模型中S=0.934。
然后分别定义41号材料T,W,L3个方向的弹性模量、屈服应变、第一切线模量、第二切线模量、屈服应力、压实应变等参数,用实体单元模拟点阵块的各向异性特征。
对于典型的弹塑性点阵材料,这些参数无法通过查表或查询相关标准得到,而是由相应方向上壳单元点阵块模型正向压缩的应力-应变曲线得到。具体方法是:将壳单元点阵块模型的应力-应变曲线简化为弹性阶段、平台阶段和压实阶段,得到预估的折线,根据折线得到各参数预估值。预估值特征点如图4所示。

图4 预估值特征点取值
点阵材料在W,L方向上是各向同性的,因此在定义材料参数时,W,L两个方向上的参数相同。图 5给出了壳单元点阵模型在W,L两个方向上的压缩力位移曲线。
2.2 点阵块的实体单元建模
以六面体实体单元建立点阵块仿真模型,实体单元卡片中定义了单元各向异性坐标系,其中第一方向是T方向,第二方向是L方向,第三方向由右手定则确定。单元网格大小为6 mm,模型整体尺寸为84 mm×44 mm×44 mm。实体单元点阵块模型与上下刚性墙接触厚度为0.6 mm,为主从接触,摩擦系数为0.1,刚性墙压缩速度为1 m/s,实体单元点阵块T向压缩模型如图6所示。
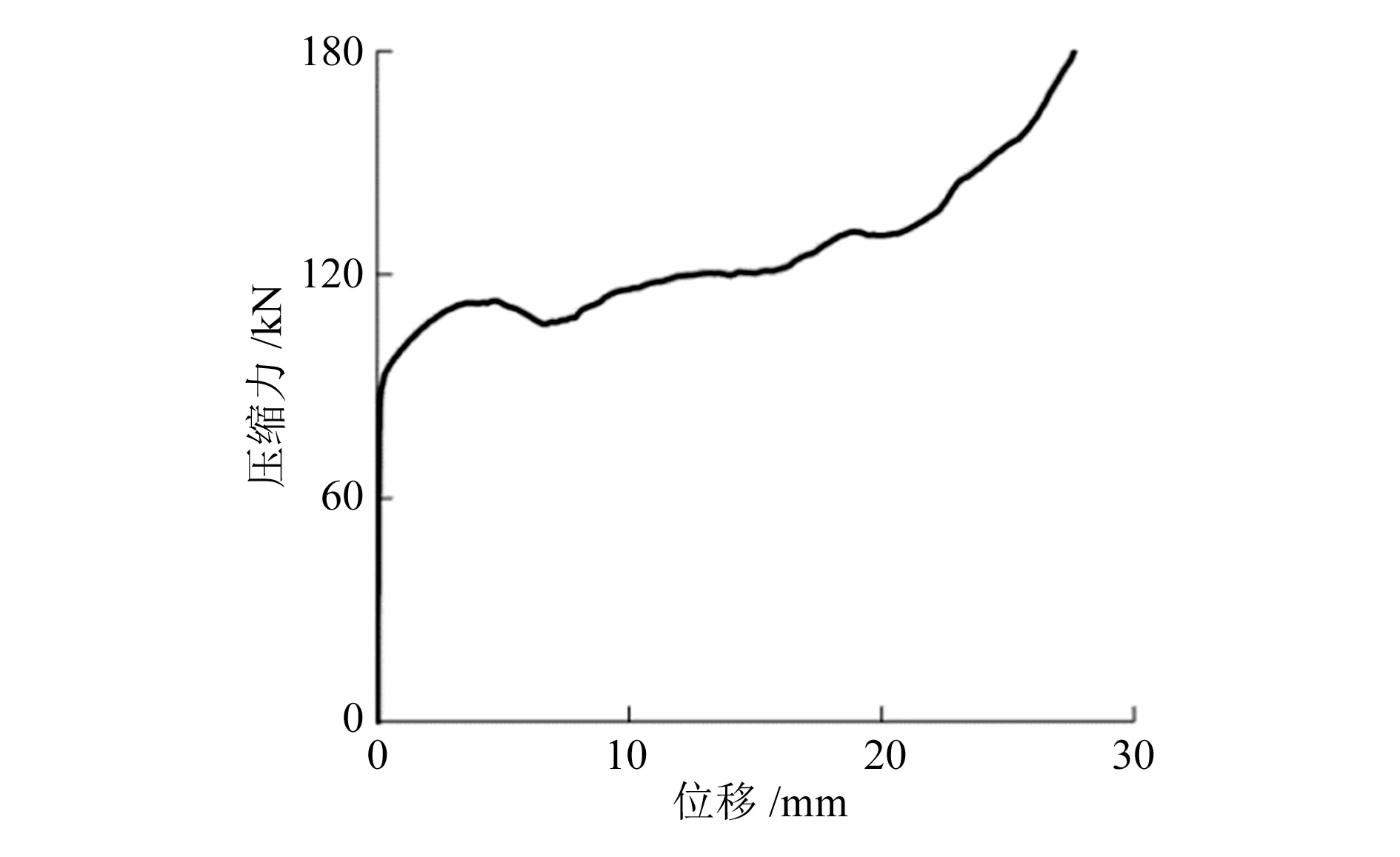
图5 壳单元点阵块模型在W、L方向上的压缩力-位移曲线
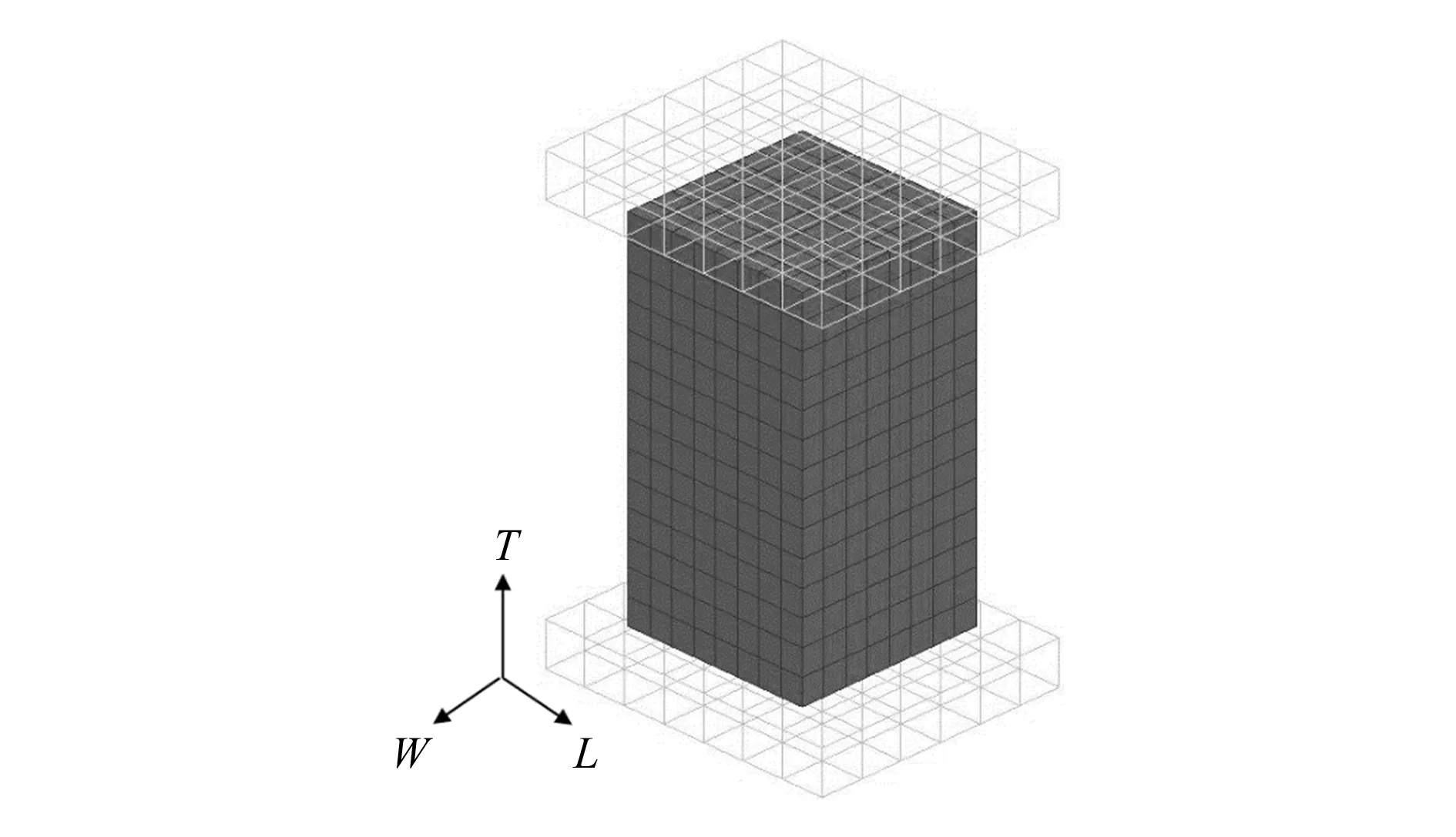
图6 实体单元点阵块T向压缩模型示意图
2.3 点阵块实体单元建模与壳单元建模的仿真结果对比
图7所示为不同时刻实体单元模型和壳单元模型的压缩过程,其中左侧是实体单元点阵块模型,右侧是壳单元点阵块模型。从图中可以看出,实体单元点阵块模型在细节上与壳单元点阵块模型不同,不能表达详细的胞元变形过程;在压缩过程中实体单元点阵块模型也观察不到塑性铰的产生与变化;实体单元点阵块模型的所有单元在T方向上均匀地变形,而壳单元点阵块模型的胞元变形程度以及变形的顺序不同;从相同时刻的压缩位移来看,两种模型在相同时刻的压缩位移大致相同。为了考察实体单元点阵块模型的吸能性能,进一步对比了两种模型的压缩力-位移曲线和内能-位移曲线,如图8和图9所示。
从图中可以看出,点阵块实体单元模型与壳单元模型的压缩力和内能随位移的变化趋势一致。
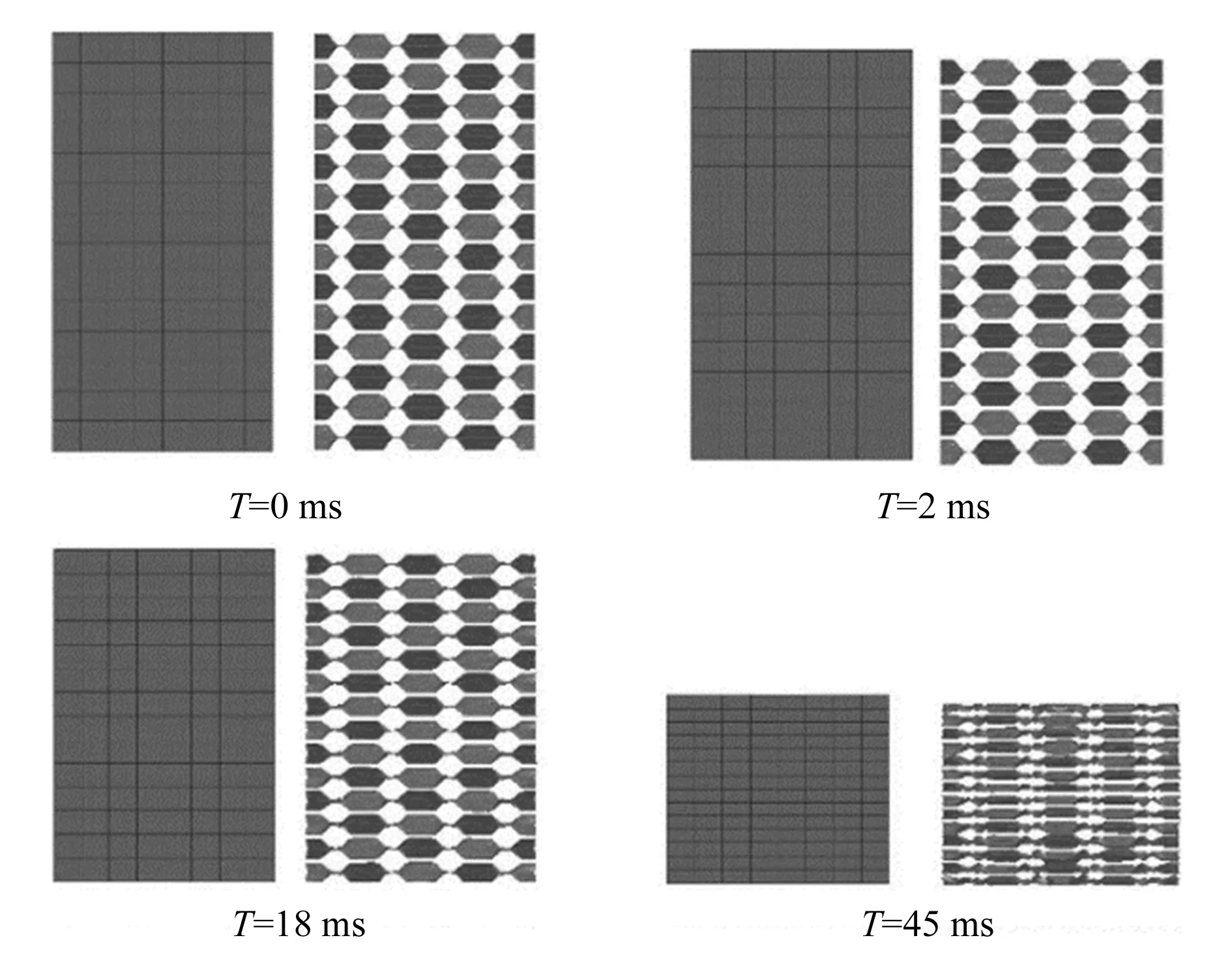
图7 实体单元模型和壳单元模型T向压缩过程对比

图8 实体单元模型与壳单元模型的压缩力-位移曲线

图9 实体单元模型与壳单元模型的内能-位移曲线
表2对比了实体单元点阵块模型与壳单元点阵块模型的吸能参数。实体单元点阵块模型在触发力、平台力平均值、压实应变以及吸能量上与壳单元点阵块模型差距很小,说明实体单元点阵块模型的吸能能力与壳单元点阵块模型相当。

表2 点阵块实体单元模型与壳单元模型吸能参数对比
表3对实体单元建立的点阵块模型与壳单元建立的点阵块模型的有限元求解参数进行了对比。由表可以看出,壳单元点阵块模型在节点个数和单元个数上都远大于实体单元点阵块模型,实体单元点阵块模型的时间步长更小,壳单元点阵块模型的求解时间远远大于实体单元点阵块模型。

表3 点阵块实体单元模型与壳单元模型求解参数对比
综合比较可知,用实体单元点阵块模型模拟点阵块体T向压缩吸能,可以得到和壳单元点阵块模型相同的吸能性能,并且实体单元点阵块模型的单元数量和求解时间远小于壳单元模型,求解效率更高。
3 结论
通过比较壳单元建立的点阵块模型和实体单元建立的点阵块模型T向压缩仿真获得的吸能特征参数以及求解参数,得到以下结论:
1)壳单元建立的点阵块模型和实体单元建立的点阵块模型T向压缩仿真获得的力-位移曲线趋势一致,均包括弹性阶段、平台力阶段和压实阶段。
2)对触发力、平台力平均值、压实应变和吸能量等指标进行比较,实体单元与壳单元点阵块模型的仿真结果差值不超过5%,说明两种建模方式下的动态压缩响应特征吻合良好。
3)用实体单元建立的点阵块模型求解时间以及单元数量都远小于用壳单元建立的点阵块模型,如果只考察吸能部件的吸能能力,用实体单元代替壳单元建模,对吸能部件进行简化能够提高求解效率。
