胞元结构准静态压缩力学行为及吸能特性研究

2022-09-23赵著杰侯海量夏习持

振动与冲击 2022年17期

赵著杰，侯海量，李典，夏习持

(海军工程大学舰船与海洋学院，武汉 430033)

胞元结构在工程之中广泛存在，凭借良好的综合力学特性，其在生物医药、交通运输、建筑结构、机械工程、减振降噪、防火隔热、分子材料、防务技术等[1-8]多领域得到了重点关注与研究。

胞元结构一般可以分为夹层结构[9]、类蜂窝结构[10]和点阵结构[11]，它们通常由板材、桁架、节点通过均匀排布、交错排布、梯度布置等方式组合而成，其制造工艺主要有焊接、热熔、电熔、铸造、3D打印等。Gibson[12]对多孔固体进行了深入的研究，从线弹性变形、弹性屈曲、塑性塌陷、脆性破坏、黏弹性、蠕变等方面总结了常见胞元结构的综合力学性能，并通过单个胞元结构的基础力学参数表征了胞元结构的诸多力学性能指标。

针对单个胞元结构的力学性能探索主要有构型研究和规格研究两大方向。在构型研究方面，基于三角形、方形、圆形等常规几何构型，内凹型、拉胀型、手性、箭型、星型、压扭型等[13-18]新颖构型先后被提出；与此同时，诸多构型设计方法也为胞元结构构型设计提供了思路:Xiang[19]受甲虫的鞘翅结构启发，提出了管壁复合仿生蜂窝胞元结构，秦浩星[20]基于SIMP拓扑优化方法，建立了任意泊松比胞元结构模型，Zhang[21]结合自相似设计方法提出分级层状蜂窝结构，研究了其在大挠度变形条件下的面内压缩特性，Shi[22]采用变分渐近法建立蜂窝夹层板的等效模型有效预测了胞元局部场的分布，为结构优化设计提供了帮助。在规格研究方面，有关研究主要针对结构壁厚、边长、内角等基础力学参数对胞元结构综合力学性能的影响：罗昌杰[23]推导得到了Y形胞元结构在异面压缩下的平均压缩应力，证明了结构规格参数与结构静、动态平均压缩应力存在直接关系，严效男[24]在对六边形聚氨酯蜂窝结构的研究中发现：胞元凹角、宽度、壁厚都会对结构泊松比和能量吸收特性产生影响，梁森[25]结合等效弹性参数计算方法开展了对蜂窝夹芯结构的研究，并针对胞元结构的壁面厚度进行了优化设计，Namvar[26]在对六边形蜂窝夹层板的优化设计中使用了多目标粒子群遗传算法，为胞元结构的规格设计提供了新思路。

船舶工程领域中，液舱、双层底隔舱等结构都是典型的胞元结构，在碰撞、搁浅、水下爆炸等情况下，这类结构通常会受到外部冲击载荷作用。本文以单个胞元结构为研究对象，考虑结构构型和规格对单个胞元结构力学特性的影响，提出了7种体积相等、构型不同的单个胞元结构，采用准静态压缩试验开展了不同壁厚下各类胞元结构的力学行为特性和结构吸能特性研究，为工程领域中的胞元结构综合性能研究提供基础。

1 试验设计

1.1 准静态压缩试验装置

准静态压缩试验装置由WANCE-ETM105D型电子万能试验机和载荷传递工装两部分组成如图1所示。最大试验压力为100 kN，压缩速度设置为5 mm·min-1，实时记录位移、压力、应力、应变数据，数据采样率为250 Hz。

图1 准静态压缩试验装置Fig.1 Quasi-static compression test device

载荷传递工装包含固定限位垫板和活动传力垫板，其中，固定限位垫板由1块20 mm厚的钢垫板和4根直径为48 mm的钢柱焊接而成，钢板下部焊有钢圈限制其位移，确保钢圈直径与万能试验机下压头直径一致。活动传力工装由1块20 mm厚的钢垫板和3块20 mm厚的传力板焊接而成，重约25.8 kg，在钢垫板中心及四周分别预制孔洞以便钢柱穿出，以保证压缩方向位于轴心处。

1.2 胞元结构

共设计七种胞元结构(见图2)。其中，W表示外凸设计方法，N表示内凹设计方法，H表示弧形胞元，L表示六边形胞元，G表示鼓形胞元；W-H和N-H分别为对照设计的外凸、内凹弧形胞元，W-L和N-L分别为对照设计的外凸、内凹六边形胞元，W-G和N-G分别为对照设计的外凸、内凹鼓形胞元，Z-Z为正方形胞元；W-L、N-L为折线型胞元，W-H、W-G、N-G、N-H为弧线型胞元。

每个胞元构型在平面XZ截面的轮廓面积相等，在Y方向的宽度均为80 mm，细部尺寸如图2(b)所示。各胞元壁面通过氩弧焊连接，在胞元上壁面设置排气管，管高度20 mm，内径6 mm，壁厚2.0 mm。

(a) 胞元结构构型

胞元结构的壁面材料选用1.0 mm、1.5 mm、2.0 mm钢板，对各型钢材进行切割取样，并对样件进行了拉伸试验如图3所示，可得钢材的屈服强度约为200 MPa，抗拉强度约为295 MPa。

图3 材料拉伸试验Fig.3 Material tensile test

1.3 试验工况

水平放置电子万能试验机、活动传力垫板、胞元结构和固定限位垫板，确保各部分的中心位于同一铅垂线上，通过摄像机记录胞元结构的准静态压缩过程。压缩试验共设置了21个工况，各工况中的胞元结构参数如表1所示。

表1 试验工况Tab.1 Working conditions

2 结构力学行为

2.1 外凸型胞元

图4为外凸弧形胞元(W-H型)的变形破坏过程。在载荷作用初期，胞元的前、后壁面最先发生了失稳屈曲和向结构外部的鼓胀弯曲，塑性铰线a和塑性铰线b1～b4先后形成，左、右壁面分别向胞元内部(箭头方向)对称收缩。受初始挠度和缺陷影响，胞元上半部分和下半部分的初始刚度有所不同，初始刚度较小的部分(区域I)最先发生失稳，刚度较大的部分(区域II)随后发生失稳。在区域I失稳之前，胞元的压缩量和前、后壁面的变形量均较小，塑性铰线a未发生大挠度变形，随后受区域I失稳的影响，塑性铰线a向下弯曲。在区域I停止变形后区域II开始变形，塑性铰线转而向上弯曲，并最终在胞元密实时恢复至平直状态。

ε=0.2

图5为外凸弧形胞元的应力应变曲线。结合变形破坏过程可以看出：在载荷作用初期，胞元的应力上升迅速，随着壁面发生失稳，应力在达到峰值后开始下降；在载荷作用中期，刚度较小的部分最先失稳变形，在结构壁面发生堆叠接触后，失稳区域的刚度得到增强，应力出现了回升；随着压缩量的进一步增加，刚度较大的部分发生失稳变形，结构应力发生二次回落；在载荷作用后期，结构整体趋于密实，应力再次迅速上升。

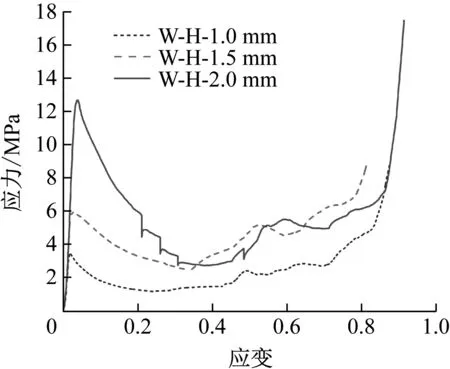
图5 外凸弧形胞元的应力应变曲线Fig.5 Stress-strain curves of convex arc cells

在结构壁面较薄(1.0 mm、1.5 mm)时，各壁面的刚度相对较低，失稳变形发展较为协调，焊缝在载荷作用前期未发生明显破坏，应力应变曲线较为平滑，结构的应力初始峰值的下降幅度较小、后屈曲软化效应较弱；在壁面较厚(2.0 mm)时，结构各壁面的刚度提高，壁面协调变形能力减弱，焊缝在前期发生了逐段的撕裂破坏，应力应变曲线中出现了多个应力骤降点，结构的应力初始峰值的下降幅度较大、后屈曲软化效应较强。

图6为外凸弧形胞元受力分析。结构的折线壁面和直立壁面变形模式有所区别：在载荷作用初期，弧线壁面受初始曲率影响，在受到载荷压力和支持力作用下呈现出向结构内部的弯曲收缩，弧线壁面外压力随着压缩量的增加而增大；直立壁面受到了载荷压力、支持力以及弧线壁面外压力的共同作用发生了失稳屈曲。由于弧线壁面拥有较好的弯曲和延展特性，其腰部和上、下两端的变形收缩量均较小，直立壁面的主要失稳区域(图6虚线)呈现为长方形，塑性铰线a和塑性铰线b1～b4先后出现。在载荷作用中后期，直立壁面沿各塑性铰线屈曲变形，弧线壁面则在其中部和上下端焊缝的约束作用下发生了弯曲收缩。

图6 外凸弧形胞元受力分析Fig.6 Force analysisof convex arc cell

图7为外凸六边形胞元(W-L型)的变形破坏过程。在载荷作用初期，塑性铰线c1～c3同时在胞元前壁面形成，随后前壁面以各个塑性铰线为轴发生了屈曲变形，左、右壁面向结构外部发生鼓胀和弯折。随着压缩量的增加，焊缝在点1处最先发生破坏，而后发生了自中部向上、下两端的撕裂，各壁面的变形挠度迅速增大直至结构发生密实。

ε=0.2

与外凸弧形胞元类似，结构壁厚和焊缝强度影响了外凸六边形胞元的变形破坏模式。在结构壁面厚度较小时，左、右壁面的弯折变形对前、后壁面产生了向结构内部的弯扭作用(箭头方向)，这导致前、后壁面的屈曲变形朝向结构内部，在壁厚增加后，壁面刚度提高，焊缝较早发生了破坏，前、后壁面与左、右壁面的协同变形作用消失，共同发生了向结构外部的花瓣状弯折变形。

图8为外凸六边形胞元的应力应变曲线。与外凸弧形胞元不同，外凸六边形胞元左、右壁面的运动趋势朝向结构外部，这使得胞元的前、后壁面受到了朝向左、右侧的拉力，前、后壁面的稳定性和胞元整体刚度得到提升，因而外凸六边形胞元的应力初始峰值较外凸弧形胞元存在明显提高。

图8 外凸六边形胞元的应力应变曲线Fig.8 Stress-strain curves of convex hexagonal cells

相比壁面较薄(1.0 mm、1.5 mm)的情况，壁面较厚(2.0 mm)的外凸六边形胞元的峰值应力回落较快，并呈现出多点骤降的情况。这是由于较高的壁厚值改变了结构的变形破坏模式：短时间内大范围的焊缝破坏导致结构承载力迅速丧失。对比壁厚为2.0 mm的外凸六边形、外凸弧形胞元的应力应变曲线可以看出，外凸六边形胞元的后屈曲软化现象更为明显。

图9为外凸六边形胞元受力分析。在压缩载荷作用于结构后，胞元的直立壁面和折线壁面分别发生了失稳屈曲和弯曲外张(图9)。在折线壁面弯曲外张的过程中，其与直立壁面的交点处(图7中的点1)出现了应力集中并导致焊缝较早的发生了失效，失效焊缝附近的直立壁面和折线壁面出现了自由边界。在自由边界出现后，折线壁面仅在自由边界附近的部分区域发生了弯曲外张，直立壁面则在自由边界附近发生了较大程度的失稳屈曲(图9虚线)：其失稳屈曲区域被塑性铰线c2对称分为了上、下两个部分，两部分分别以塑性铰线c1、c3为界线发生进一步的对称屈曲变形。最终，结构的主要失稳区域产生了大幅度弯曲变形直至结构被压至密实，结构其他区域的变形量则相对较小。

图9 外凸六边形胞元受力分析Fig.9 Force analysis of convex hexagonal cell

图10为外凸鼓形胞元(W-G型)的变形破坏过程。在载荷作用初期，外凸鼓形胞元的前壁面沿塑性铰d1～d3发生了失稳屈曲，左、右壁面则产生了往外侧的弯曲变形。随着压缩过程的进行，薄弱处焊缝发生失效，各壁面发生了大挠度变形，结构最终被压至密实。

ε=0.2

与外凸六边形胞元的折线型壁面不同，外凸鼓形胞元的左、右壁面为曲线形壁面，各壁面在弯曲变形过程中的变形较为协调，未出现类似于图7点的结构焊缝破坏。在壁面较薄(1.0 mm、1.5 mm)时，前、后壁面向结构内部的变形对左、右壁面产生了拉伸作用，塑性铰e形成后，左、右壁面呈现出多角度弯曲变形，在壁面较厚(2.0 mm)时，焊缝由底部向上部发生破坏，各壁面皆向外发生了花瓣状弯曲变形。

图11为外凸鼓形胞元的应力应变曲线。受左、右壁面的拉伸作用，外凸鼓形胞元的前、后壁面刚度和结构的应力初始峰值较外凸弧形胞元均得到了提高。结合变形破坏过程可以看出，在结构壁面较薄(1.0 mm)时，焊缝未发生明显破坏，应力变化较为平缓。在结构壁面较厚(2.0 mm)时，结构失稳导致初始峰值应力下降后，左、右弧形壁面的弯曲变形较平稳，焊缝撕裂过程较为缓慢，应力值未出现断崖式骤降。

图11 外凸鼓形胞元的应力应变曲线Fig.11 Stress-strain curves ofconvex bulbouscell

在壁面厚度为1.5 mm时，受焊接缺陷影响，结构前壁面、右壁面相交处的焊缝在载荷作用初期即发生了失效，结构的变形破坏模式也因此改变：在单一焊缝破坏后，结构产生了两条自由边，其余焊缝受壁面拉伸作用而破坏的可能性大大降低，胞元的前、后壁面出现了类似图4中b1～b4的塑性铰线，相比较塑性铰线d1～d3，这种屈曲变形模式提升了前、后壁面的塑性变形耗能能力，胞元的应力值产生了一定的波动但未出现明显的下降，结构的后屈曲软化效应有所减弱。

图12为外凸鼓形胞元受力分析。外凸鼓形胞元的直立壁面和折线壁面的变形模式与外凸六边形类似，即分别发生了失稳屈曲和弯曲外张，但两者变形的区域也有所区别：弧线壁面拥有较折线壁面更好的弯曲特性，其与直立壁面交界处焊缝的应力分布较为均匀，焊缝较难发生撕裂，因而弧线壁面呈现出整体的弯曲外张，此时直立壁面主要失稳区域(图12虚线)的屈曲也较为完全，塑性铰线d1和d3分别出现在了上壁面、下壁面附近，胞元整体未出现类似外凸六边形胞元壁面的部分屈曲现象。

图12 外凸鼓形胞元受力分析Fig.12 Force analysis of convex bulbous cell

图13展示了各类外凸胞元的应力应变曲线。总的来看，曲线大致可分为两类，一类如外凸六边形和外凸鼓形胞元，其侧壁面在变形过程中呈现为弯曲回缩，这破坏了直立壁面的局部稳定性和承载能力，胞元在载荷作用初期的峰值应力较高，应力初始峰值的持续时间较长，后屈曲软化效应较弱；另一类如外凸弧形胞元，其侧壁面在变形过程中呈现为弯曲外张，直立壁面的局部稳定性和承载能力得到增强，胞元在载荷作用初期的峰值应力较低，应力初始峰值的持续时间较短，后屈曲软化效应较强。从图中还可以看出，由于折线型壁面外张力大于曲线形壁面，外凸六边形胞元的整体承载能力(初始峰值应力)较外凸弧形胞元有了一定的提升，然而由于焊缝易于发生撕裂从而导致结构整体失稳，外凸六边形胞元在结构变形中后期(应变值为0.2～0.7)的应力值下降较为明显。

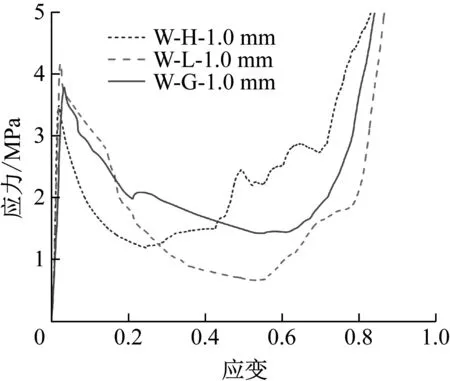
图13 外凸胞元的应力应变曲线Fig.13 Stress-strain curves of convex cells

2.2 正方形胞元

图14为正方形胞元(Z-Z型)的变形破坏过程。受结构的对称性影响，在载荷作用初期，结构的前壁面形成了与外凸鼓形胞元类似的塑性铰线(f1～f3)，每个壁面沿各自的塑性铰线发生了方向不一的屈曲变形：左、右壁面向外凸出，前、后壁面向内凹陷。胞元壁面厚度亦会显著改变正方形胞元的变形破坏模式，当胞元壁面厚度较大时，结构焊缝会较早发生破坏，各壁面皆向内发生了变形，随后呈现出花瓣状弯折破坏。

ε=0.2

图15为正方形胞元的应力应变曲线。可以看出，随着壁面厚度的增加，正方形胞元应力初始峰值的增长规律与外凸弧形、外凸鼓形胞元保持一致。然而对于壁面较厚(2.0 mm)的正方形胞元，其在失稳后的应力值波动剧烈，结构应力一度下降到了0.07 MPa，这是由于此工况中正方形胞元的四周焊缝同时发生了破坏，相比于焊缝为折线型或弧线型的胞元，正方形胞元直线型焊缝的撕裂失效过程极为迅速，结构的自由边迅速增至8条，各壁面短时间内发生了大挠度弯曲变形，结构应力值骤降，后屈曲软化现象尤为明显。

图16为正方形胞元受力分析。在载荷作用初期，结构的各壁面均产生了与外凸鼓形胞元直立壁面类似的塑性铰线f1～f3，区别在于正方形胞元与垫板的接触面积更大，结构失稳区域(图15虚线)的面积有所增加，由于正方形胞元各壁面均不存在明显的初始曲率，其前、后壁面的屈曲变形方向(向内屈曲或向外屈曲)与左、右壁面保持相反，且屈曲方向存在着一定的随机性，实际的结构屈曲方式与壁面的初始挠度等因素有关。

图15 正方形胞元的应力应变曲线Fig.15 Stress-strain curves of square cell

图16 正方形胞元受力分析Fig.16 Force analysis of square cell

2.3 内凹型胞元

图17为内凹鼓形胞元(N-G型)的变形破坏过程。在载荷作用初期，左、右壁面最先发生失稳并向结构内部产生扭转变形(箭头方向)，受该变形的挤压作用，前、后壁面发生了朝向结构外部的弯曲变形，塑性铰h、g1～g4先后形成。随着压缩量的增加，左、右壁面收缩量不断增加，受到其协同变形作用，上、下壁面的发生了向结构内部的弯曲变形。与外凸鼓形胞元有所不同，内凹鼓形胞元的变形破坏模式未因壁面厚度改变而发生明显变化，胞元各壁面的变形过程较为协调，未出现明显的焊缝受拉破坏现象。

ε=0.2

从内凹鼓形胞元的应力应变曲线如图18可以看出，其应力应变曲线较为光滑，未出现焊缝失效导致应力骤降的现象，后屈曲效应较弱。对比不同壁厚的内凹鼓形胞元，各胞元的应力应变曲线形貌大致类似；对比相同壁厚的内凹鼓形胞元和外凸鼓形胞元，外凸鼓形胞元的应力初始峰值较内凹鼓形胞元提高了约1.5倍～2倍，这说明内凹鼓形构型尽管降低了胞元多条焊缝同时撕裂失效的可能，但较易失稳的内凹壁面也减小了胞元整体刚度，胞元应力的初始峰值下降明显。

图18 内凹鼓形胞元应力应变曲线Fig.18 Stress-strain curves ofconcave bulbous cell

图19是内凹六边形胞元(N-L型)的变形破坏过程，与内凹鼓形胞元相类似：胞元的前、后壁面发生了向结构外部的弯曲变形，产生了横向塑性铰i和双“V”型塑性铰j1～j4；左右壁面产生了向结构内部的折叠变形，受该折叠变形产生的协同作用，胞元的上、下壁面出现了一定的弯曲变形。

ε=0.2

对比内凹六边形胞元(图19)和内凹鼓形胞元(图17)的变形破坏过程可以发现，两者壁面的变形及耗能模式相似：对于内凹六边形胞元的前(后)壁面，其绕塑性铰线i变形的区域与内凹鼓形胞元对应区域的形状、面积基本一致，绕塑性铰线j1～j4变形的区域面积则较小，基本可以忽略；对于内凹六边形胞元的左(右)壁面，其绕腰部塑性铰线变形的区域形状、面积与内凹鼓形胞元相近。因而两类胞元壁面的塑性变形过程以及能量消耗规律类似，应力应变曲线(图18，20)特征也极其相似。

“新生儿睾丸扭转短时间内即可发生坏死，同时可能会引起全身炎症反应及影响另一侧睾丸，必须急诊手术，需紧急转到一师医院救治……”陈正副院长在询问患儿病情后，立即与一起参加义诊的一师医院小儿外科援疆专家钱云忠主任和泌尿外科方家杰副主任进行实时会诊，同时将患儿的检查结果和相关资料通过微信传给了其后方医院——浙江大学医学院附属儿童医院的泌尿外科专家徐珊主任，在返程的车上共同商讨和制定了周详的手术方案，指导赵主任立即进行手术前相关检查并联系120中心马上进行新生儿转运，争取为抢救患儿节省时间。

内凹弧形胞元(W-H型)的变形破坏过程与内凹鼓形、六边形胞元略有不同(图21)：一方面，内凹鼓形、六边形胞元均存在明显的焊缝应力集中点(图17中的点2、图19中的点3)，焊缝较早发生了失效，内凹弧形胞元的焊缝应力分布较为均匀，焊缝发生失效的时间较晚。另一方面，内凹鼓形、六边形胞元的左、右壁面通过弯折制成，弯折线在变形过程中成为了天然塑性铰线，结构的失稳过程发展迅速；内凹弧形胞元的左、右壁面则无天然塑性铰线，结构的失稳过程较为缓慢。

图20 内凹六边形胞元应力应变曲线Fig.20 Stress-strain curves of concave hexagonal cell

ε=0.2

图22是内凹弧形胞元的应力应变曲线。与内凹鼓形、六边形胞元相比，内凹弧形胞元的应力初始峰值较高，峰值回落的速度也较慢。这一现象受两大因素影响：一方面，折线型胞元结构的多壁面交界点易于成为变形过程中的应力集中点和优先失效位置，这一现象在弧线型胞元结构中则不明显；另一方面，多壁面交界点处的焊接质量较难保证，这加剧了交界点破坏的可能性，结构的极限承载力和后屈曲刚度因而降低。

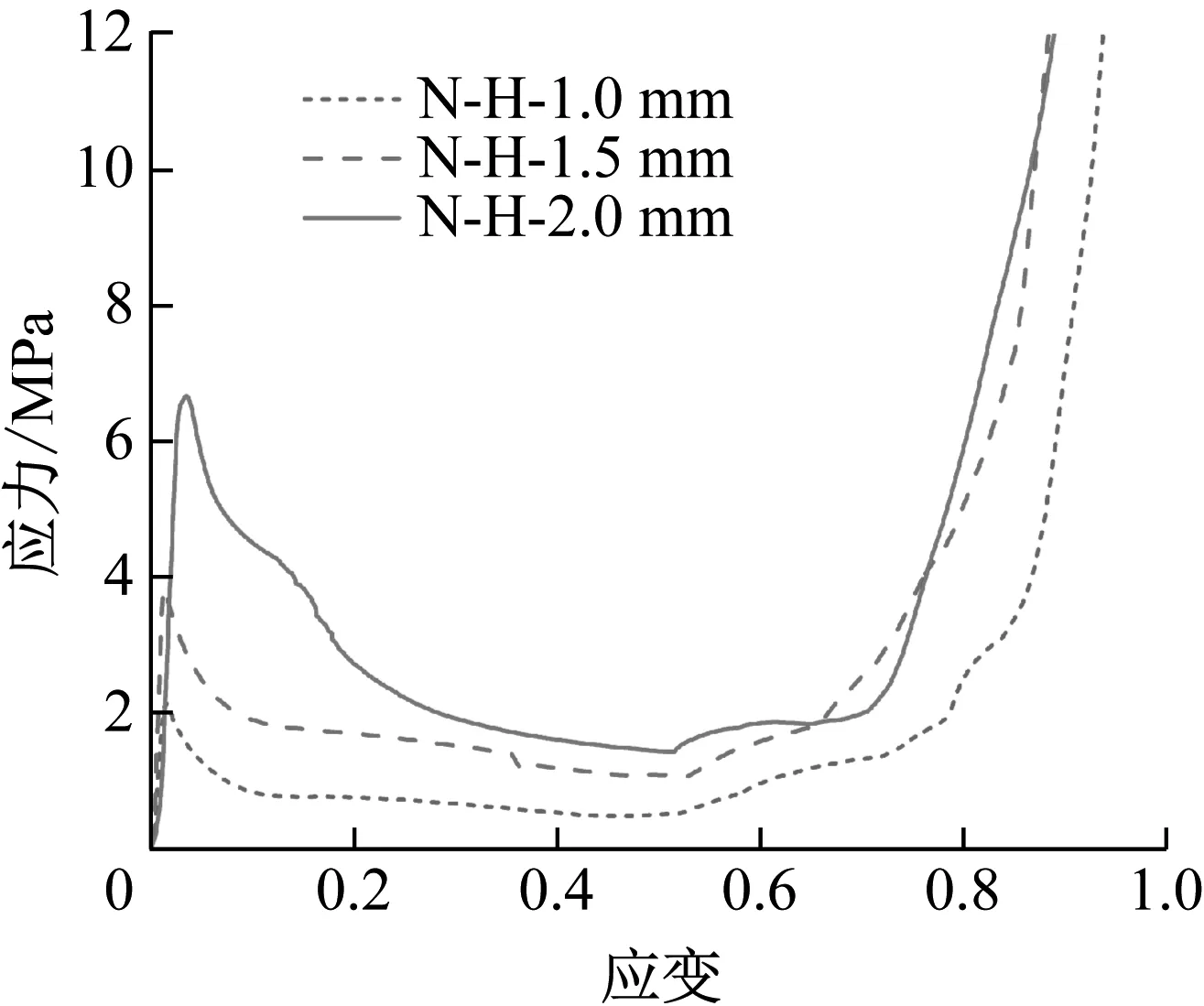
图22 内凸弧形胞元应力应变曲线Fig.22 Stress-strain curves of concave arc cell

图23为内凹形胞元受力分析。压缩载荷主要由胞元的直立壁面和内凹壁面(内凹弧线壁面或内凹折线壁面)两部分承担。在载荷作用初期，内凹曲面出现了向结构内部的弯曲收缩变形，胞元腰部区域最先发生失稳，塑性铰线i最先形成。随着压缩量的增加，左、右壁面收缩运动量逐步增加，直立壁面对称形成了塑性铰线j1～j4并沿各铰线发生了多区域的失稳屈曲。在载荷作用中期，内凹壁面沿腰部中线处进一步弯曲收缩，直立壁面则主要以塑性铰线i为轴向结构外部屈曲外张。在载荷作用后期，结构的直立和内凹壁面分别发生了部分堆叠，结构逐步被压至密实化。与外凸形胞元不同，内凹形胞元直立壁面的边缘区域在铰线j1～j4处发生了大变形，这对直立壁面与内凹壁面连接处的焊缝起了一定的保护作用，胞元结构在压缩的前期和中期未出现明显的焊缝破坏现象。

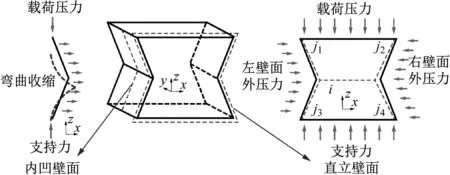
图23 内凹形胞元受力分析Fig.23 Force analysis of concave cell

图24展示了各类内凹形胞元的应力应变曲线。总体上看，内凹形胞元的应力应变曲线变化规律与外凸弧形胞元大体类似但略有区别：内凹形胞元的应力初始峰值的持续时间较短，后屈曲软化效应较强，但应力初始峰值低于外凸弧形胞元。一方面，由于内凹形胞元的内凹壁面发生了与外凸弧形胞元的弧线壁面类似的弯曲收缩变形，这降低了胞元的整体稳定性，使得应力应变曲线初始峰值持续了较短时间便发生了下降；另一方面，受构型因素影响，外凸弧形胞元的弧线壁面的腰部收缩量较小，这在一定程度上提高了胞元的整体刚度，从而使得外凸弧形胞元的应力初始峰值高于内凹形胞元。

图24 内凹胞元的应力应变曲线Fig.24 Stress-strain curves of concave cells

2.4 宏观泊松比特性

在载荷作用后期，胞元的应力值第二次达到初始峰值应力后，结构进入密实化阶段。测量各胞元进入密实化阶段后的壁面变形形貌，得到了各胞元的宏观泊松比μ

(1)

式中:εx为胞元横向宏观应变值;εz为胞元垂向宏观应变值;x1和x2分别为压缩前和密实化后胞元左、右壁面几何中心连线的长度(mm);z1和z2分别为压缩前和密实化后胞元上、下壁面几何中心连线的长度(mm)。

图25比较了各个胞元的宏观泊松比与初始峰值应力。可以看出：壁厚不同、构型一致的胞元的宏观泊松比数值相近：N-H、N-L、N-G型胞元呈现出宏观负泊松比，W-L、W-G、Z-Z型胞元呈现出宏观正泊松比，W-H型胞元呈现为宏观近似零泊松比。在胞元壁面较薄(1.0～1.5 mm)时，初始峰值应力受宏观泊松比影响较小，在胞元壁面较厚(2.0 mm)时，初始峰值应力受宏观泊松比影响较明显。

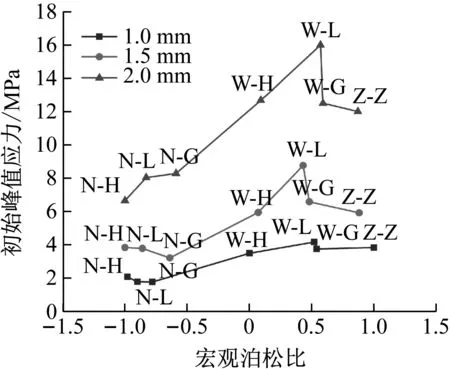
图25 胞元宏观泊松比与峰值应力关系Fig.25 Macroscopic Poisson’s ratio versus peak stressfor cells

3 结构吸能特性

胞元结构的单位质量吸能水平体现了其结构综合吸能特性，通过比吸能值表征各胞元的结构吸收特性

(3)

式中:SEA为胞元的比吸能值(J/kg);F为载荷压力值(kN);z为胞元的垂向压缩量(mm);M为胞元质量(kg)。图21(a)～(c)分别比较了壁厚为1.0 mm、1.5 mm、2.0 mm的各类胞元的SEA变化规律。

(a) 胞元壁厚1.0 mm

图27展示了各类胞元比吸能值随应变值变化的关系曲线。总体来看，各类胞元的SEA值均随应变值的增加而提高，各外凸胞元的SEA值高于内凹胞元。在外凸胞元中，外凸鼓形胞元(W-G)的结构综合吸能特性较好，外凸六边形胞元(W-L)的综合吸能特性较一般；在内凹胞元中，内凹弧形胞元(N-H)的综合吸能特性较好，内凹六边形胞元(N-L)的综合吸能特性较一般。

图27 不同壁厚下各类胞元的比吸能值变化规律Fig.27 The variation pattern of specific energy absorption values for cells with different wall thicknesses

记录应变值为0.8时各胞元的比吸能值，比较不同壁厚下各内凹、外凸胞元的比吸能值差异(图27)。从图中可以发现，对于外凸胞元(W-H型、W-L型、W-G型)，在壁面较薄(1.0～1.5 mm)时，胞元比吸能值随着壁面厚度的增加而增加，在壁面较厚(1.5～2.0 mm)时，胞元比吸能值则随着壁面厚度的增加而减小。这一现象与壁面不同的变形模式有关：在胞元壁厚较小时，各壁面更易于屈曲，焊缝不易破坏，后屈曲软化效应不明显，各壁面的协同变形作用有效提升了结构耗能能力，胞元的比吸能值随壁厚的增加而增加；在胞元壁厚较大时，各壁面不易于屈曲，焊缝较易发生破坏，后屈曲软化效应明显，各壁面的协同变形作用较弱，因而导致胞元的比吸能值随壁厚的增加而降低。

对于内凹胞元(N-G型、N-L型、N-H型)，各胞元的比吸能值均随着壁面厚度的增加而增加，这与内凹结构的宏观负泊松比特性有关：在压缩过程中，壁面向结构内部的收缩变形保护了胞元焊缝，保证了结构各壁面的协调变形，在焊缝失效后，向结构内部运动的壁面对结构产生了一定的支撑作用，后屈曲软化效应得到减弱，因而在壁面厚度较大时，各内凹胞元未出现比吸能值随壁厚的增加而降低的现象。