非线性能量汇胞元减振效率分析1)
2023-12-16李孙飚
李 猛 李孙飚 丁 虎
(上海大学力学与工程科学学院,上海市应用数学和力学研究所,上海 200444)
引言
很多情况下,振动都是不利因素[1].比如,建筑结构的振动和交通工具运行时的振动会带来不可忽视的安全问题[2-3].为了减少有害振动,人们已经设计了许多减振装置[4-5].非线性能量汇(nonlinear energy sink,NES)作为一种非线性的被动减振器,因其减振频带宽、减振效果好、不需要额外消耗能量等诸多优点,受到了持续而广泛的关注[6-7].对NES 的结构设计和力学特性已经有了很多广泛而深入的研究,但是其工程应用的研究却十分有限.因此,探究使得NES 能够便捷、可靠和高效地应用到工程实际中的方式十分重要.
近20 年来,众多研究表明,NES 中存在的非线性刚度可以使得主系统产生丰富的动力学现象[8-9],包括混沌、分岔和调制响应等[10-13].特别是,NES 可以使得系统产生高效的能量靶向传递现象,使得主系统的能量以不可逆转的方式传递至NES 中,最终转化为NES 的机械能和阻尼耗散能[14-18].作为非线性减振器,NES 可以在宽频范围内稳定吸收主系统的能量,以此达到良好的减振效果[6].为了进一步的研究和应用,人们也对NES 的结构进行了众多的设计,包括轨道型NES[19]、杠杆型NES[20]、具有组合非线性阻尼的NES[21]和黏弹性NES[22]等.
对于各种振动问题,NES 均表现出了良好的减振作用.例如对于整星系统[23]、机翼结构[24]、深海柔性张力腿[25]、悬臂薄板[26]、线性镗杆系统[27]和简支输液管道[28]等结构的振动,NES 均具有良好的减振效果.在应用NES 进行减振的研究中,也不乏一些实验研究.刘中坡等[29]通过实验证明了NES 具有良好的宽频减振效果.姚红良等[30]通过实验验证了可调永磁双稳态NES 对悬臂梁的瞬态时域响应和稳态频域响应都有很好的振动抑制能力.Geng等[31]提出了可以封装的限幅型NES,并通过实验证明了限幅型NES 在限制NES 振子振幅的同时产生了比没有限位的NES 更好的减振效果,而且能够对不同模态的振动进行减振.Ding 等[32]提出了胞元化NES 分布式减振策略,并应用于弹性梁的多模态减振,从理论上证明了该策略的有效性.目前关于NES 应用的探究中,针对不同振动主结构的NES 的设计具有个性化的特性,其普适性并不高.因此,如何将NES 以高效和便捷的方式应用于不同工程结构的减振,是目前面临的挑战.
针对以上问题,本文设计了NES 胞元策略,并探讨了NES 胞元的减振效果与优势.本文对NES胞元的减振效果进行分析,研究NES 胞元减振的规律,以期为NES 的工程应用提供理论依据.
2 动力学方程及近似解析解
本节将首先建立偏心转子激励下n个NES 胞元耦合单自由度振子组成的系统的运动微分方程,之后采用复化平均法获得系统响应的近似解析解.最后给出对系统响应的近似解析解进行稳定性判断的方法.
2.1 动力学方程
偏心转子激励下n个NES 胞元耦合单自由度振子组成的系统的力学模型如图1 所示.
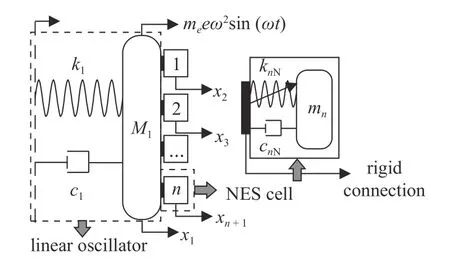
图1 力学模型图Fig.1 Mechanical model diagram
系统的运动微分方程为
式中,M1,c1和k1分别代表主振子的质量、阻尼和刚度,n代表NES 胞元的个数,mp(p=1,2,···,n),mk,cpN(p=1,2,···,n)和kpN(p=1,2,···,n)分别代表第p个NES 胞元振子的质量、框架的质量、阻尼和非线性刚度,me,e和ω分别代表偏心转子的质量、偏心距和频率,x1,xp+1(p=1,2,···,n)和t分别代表主振子的位移、第p个NES胞元质心的位移和时间.NES 的参数满足如下条件
2.2 近似解析解
为了运算方便,引入如下变量替换
其中,φ10和 φ20分别为系统处于稳态响应时 φ1和φ2的值.将变换(4)代入方程组(1),再将每个方程两端同时乘以eiωt,之后在一个激励周期上对方程进行平均,可以得到如下慢变方程组
对式(6)和式(7)组成的方程组的不动点进行代数运算,得到系统稳态响应幅值满足的非线性方程组
方程组(8)是非线性方程组,可以用伪弧长法求解.此外,方程组(8)的第二式是系统的慢不变流形(slow invariant manifold,SIM).将所求得的| φ10|和|φ20|代入式(5)可以得到主振子和NES 的位移幅值x1max和x2max分别为
将位移幅值乘以ω2,得到主振子和NES 的加速度幅值a1max和a2max分别为
2.3 稳定性分析
对解(9)的稳定性可以通过非线性微分方程组式(6)和式(7)来判断.将微分方程(7)代入式(6),消去 φ1,可以得到仅关于φ2的微分方程
将代换(12)代入式(11),得到仅关于扰动量δ的微分方程.将扰动运动微分方程线性化之后,得到该方程的一次近似微分方程.可以通过判断一次近似微分方程雅可比矩阵特征值实部的正负来判断解的稳定性.若雅可比矩阵的特征值全为负,则方程的解稳定;若雅可比矩阵的特征值存在正值,则方程的解不稳定;若雅可比矩阵的特征值全为0,则方程的解处于稳定与不稳定的临界情况.
2 NES 胞元的减振效果分析
将系统的参数设置为:M1=15.9273 kg,c1=3.36163 N·s/m,k1=33795.8 N/m,e=0.0092 m,me=0.0362 kg,cN=1 N·s/m,mk=0.05 kg.对于小重量NES 胞元,取m=0.1101 kg;对于大重量NES 胞元,取m=0.2541 kg.假设NES 胞元的个数在0~4 之间变化.下面考察NES 胞元的非线性刚度kN对减振效率的影响规律.采用1.1 节给出的方法,可以求出主振子耦合不同个数NES 胞元时的幅频曲线,如图2所示.与此同时,利用龙格-库塔法对方程组(1)进行数值运算来求得系统幅值,以验证近似解析结果的正确性.而小重量NES 占主振子重量的比例βs以及大重量NES 胞元占主振子重量的比例βl如表1 所示.
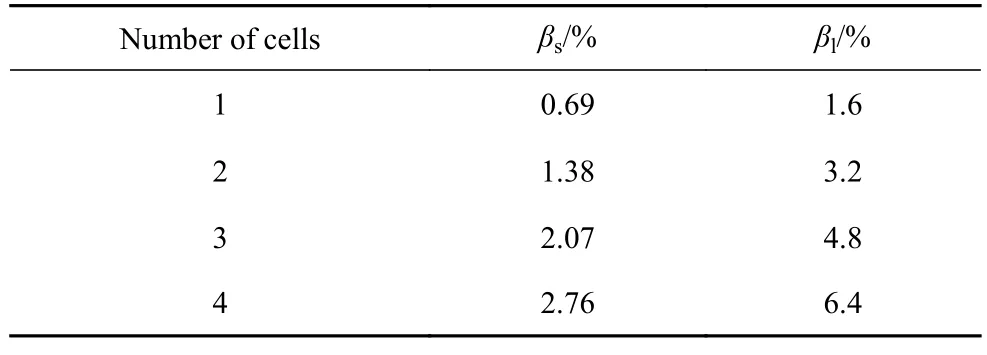
表1 NES 胞元重量占比Table 1 NES cell weight ratio
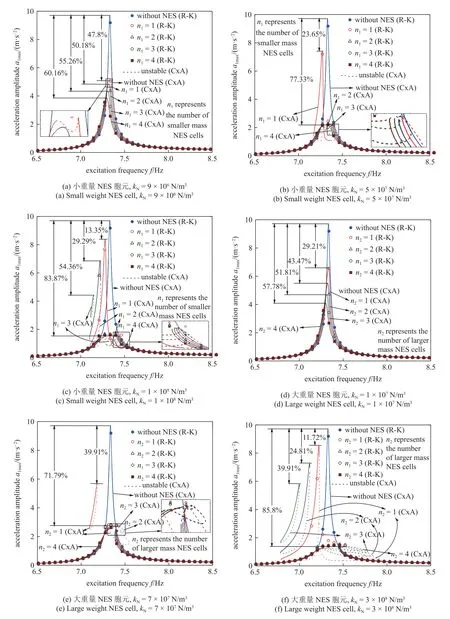
图2 非线性刚度对NES 胞元减振效果影响的分析Fig.2 Analysis of the influence of nonlinear stiffness on NES cell damping effect
可以看出,NES 胞元占主振子的最高比重也仅为6.4%,表明NES 胞元对主系统重量的影响较小.
在本文中,NES 胞元的减振效率采用如下表达
其中,a1max和a1max(withNEScells)分别表示有无加装NES 胞元时主振子的加速度幅值.而激励频率以f表示,其和对应的角频率ω的关系为
从图2 可以得出4 条规律.(1) 存在最佳的非线性刚度,使得相同数量的NES 胞元具有最佳的减振效率,高于或低于此值都会降低其减振效率.例如,在采用大重量NES 胞元的情况下,当n2=2 时,kN=7×107N/m3时的减振效率最高,当kN大于此值时,会由于系统在共振峰左侧鞍结分岔的出现导致其减振效率慢慢降低;当kN小于此值时,系统的响应越来越稳定,但是由于其刚度较小,NES 胞元弹性恢复力的作用也越来越小,导致其减振效率变低.(2) NES胞元的最佳减振非线性刚度随着其个数的增加而增加.从图2 可以看出,增加NES 胞元的个数会抑制其SN 分岔以及频率岛的产生.而NES 胞元最佳非线性刚度的增加不能持续增加其减振效率正是由于SN 分岔的存在.所以NES 胞元的个数越多,其最佳非线性刚度也越高.(3) NES 胞元可以具有良好的减振效率.小重量NES 胞元和大重量NES 胞元的最大减振效率分别达到了83.87%和85.8%.(4) 一般来讲,NES 胞元的减振效率随着个数的增加而增加.
由于NES 没有线性刚度,自身不存在共振频率,因而能够实现振动能量从主结构向NES 的靶向转移,这也是NES 能够胞元化共同作用减振的原因.也正是因为振动能量的靶向转移,NES 胞元化后,振动能量分布到各个NES 胞元中,从而减小了单个NES 的能量接收,避免了强激励环境中NES 强非线性引起的SN 分岔和频率岛现象,提高了减振的效率.另外,NES 对共振频率的自适应性能够使得NES 胞元适用于多模态结构不同位置处不同频率的减振.这是调谐质量阻尼器所不具备的.
相对单个NES 来说,NES 胞元具有多种优势.首先,NES 的减振需要一定的质量比,而当主系统质量很大时,需要很大的NES 质量.但是对应于大质量NES 所需要的强非线性刚度在实现上存在很大困难.NES 胞元能以较小的单个胞元质量克服这一困难.其次,在对不同结构进行减振时,NES 胞元具有极大的灵活性和多变性,便于以各种形式进行布置.另外,多个胞元共同作用,也能够增强应用中的可靠性.这些优势都便于NES 胞元的工程应用.
3 系统响应特征分析
多NES 胞元耦合线性振子组成的系统具有多种响应机制,包括稳态响应,强调制响应等.本节将分析NES 处于不同个数时系统的响应特征.主要针对频率岛及共振区附近的响应进行分析.
3.1 频率岛响应特征
如图2(e)所示,频率岛的上分支为稳定响应,下分支为不稳定响应,而频率岛下方的主曲线为稳定响应.取激励频率f=7.177 Hz,NES 胞元个数为1,通过R-K 方法可以得到图2(e)中频率岛上分支和其下方主曲线上的点对应的时程图与相位图,如图3所示.此时系统的参数与图2(e) 对应的系统参数相同.而f=7.177 Hz 对应频率岛上分支最高点附近.
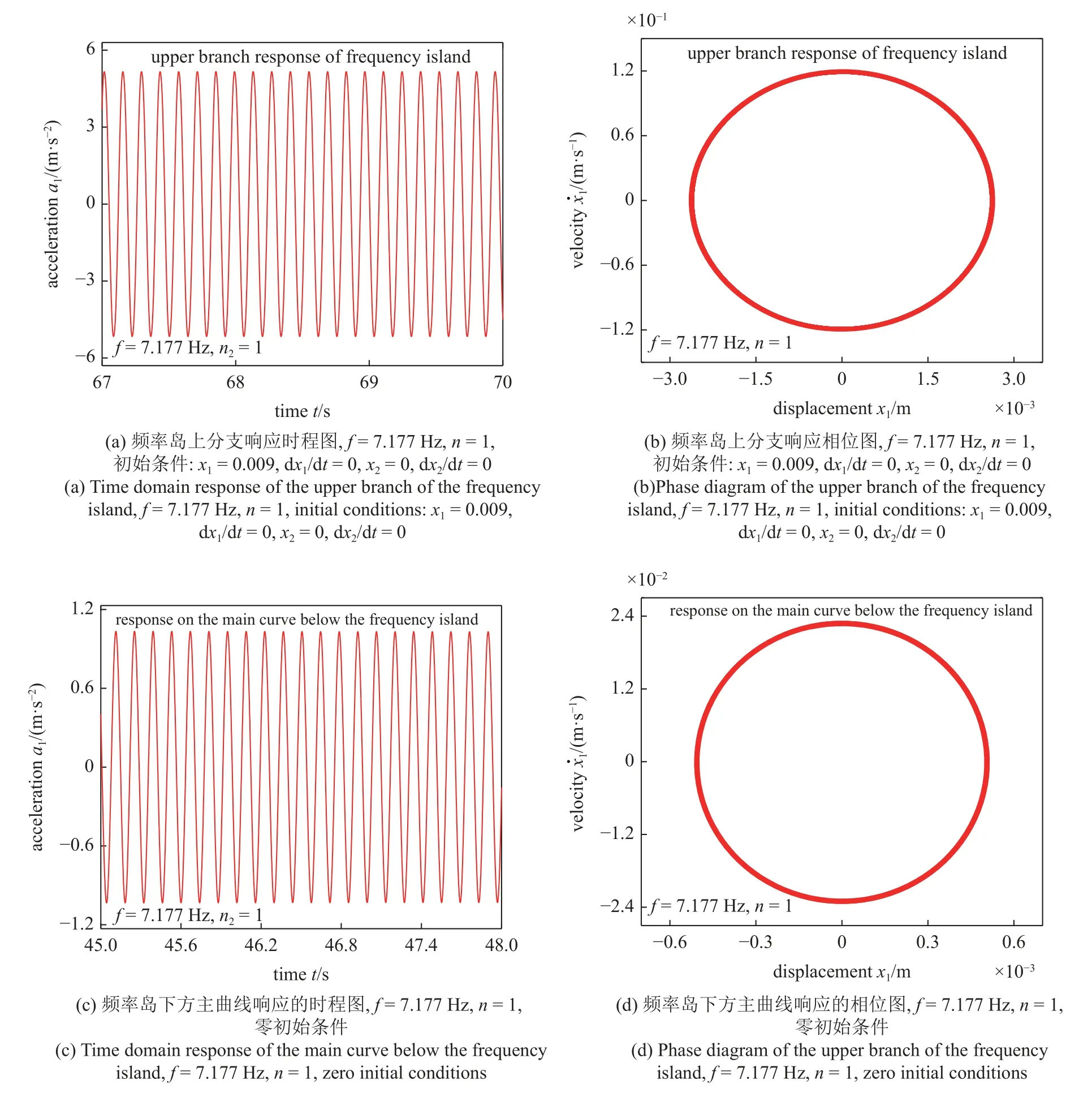
图3 频率岛上分支及其下方主曲线的时程图与相位图Fig.3 Time domain response and phase diagram of the upper branch of the frequency island and main curve below it
从图3 可以看出,不同的初始条件可以使得系统的响应处于不同的稳定状态.改变主振子的初始位移可以使得系统响应处于频率岛的上分支.而通过图3(a)与图3(c)可以知道,系统处于频率岛的上分支时,其响应幅值比同频率下频率岛下方主曲线上的响应幅值高出很多,且为稳定状态.而在工程实际中,初始条件往往不能精确控制.因此频率岛的出现在工程实际中可能带来很大的安全隐患.而NES胞元个数的增加可以有效抑制频率岛的产生,进而具有重要的意义.
3.2 共振区响应特征
通过图2(c)可以知道,系统在共振区的响应较为复杂,可以表现出稳定响应和不稳定响应.而且随着胞元个数的增加,其响应状态会发生多种变化.采用图2(c)对应的系统参数,并将激励频率固定到共振区,此处取f=7.346 Hz.利用R-K 方法绘制时程图和相位图可以研究系统在共振区的响应特点.本小节绘制出了NES 胞元个数分别取1,2,4 和9 时,系统的时程图与相位图,如图4 所示.
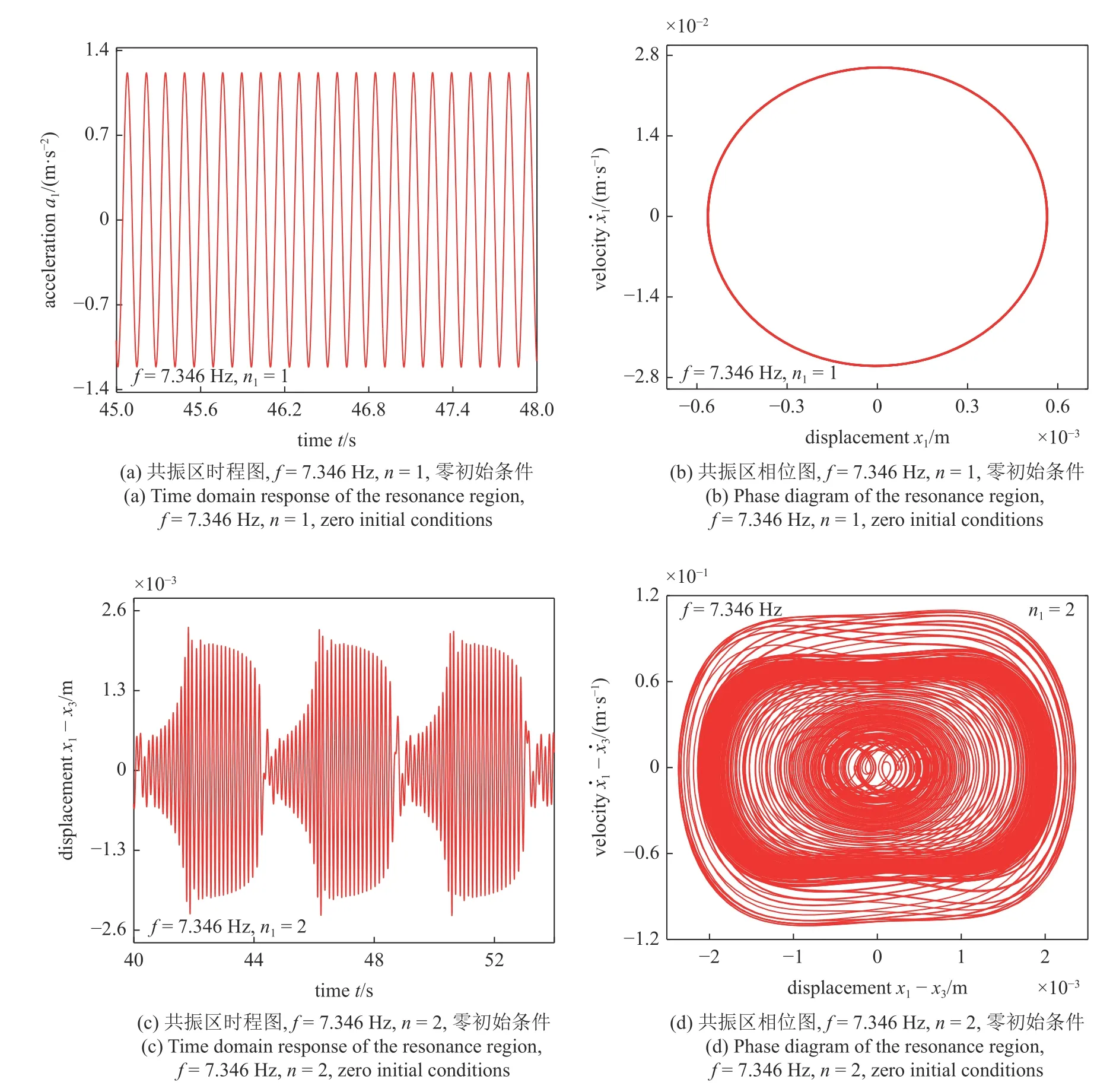
图4 共振区的时程图与相位图Fig.4 Time domain response and phase diagram of the resonance region
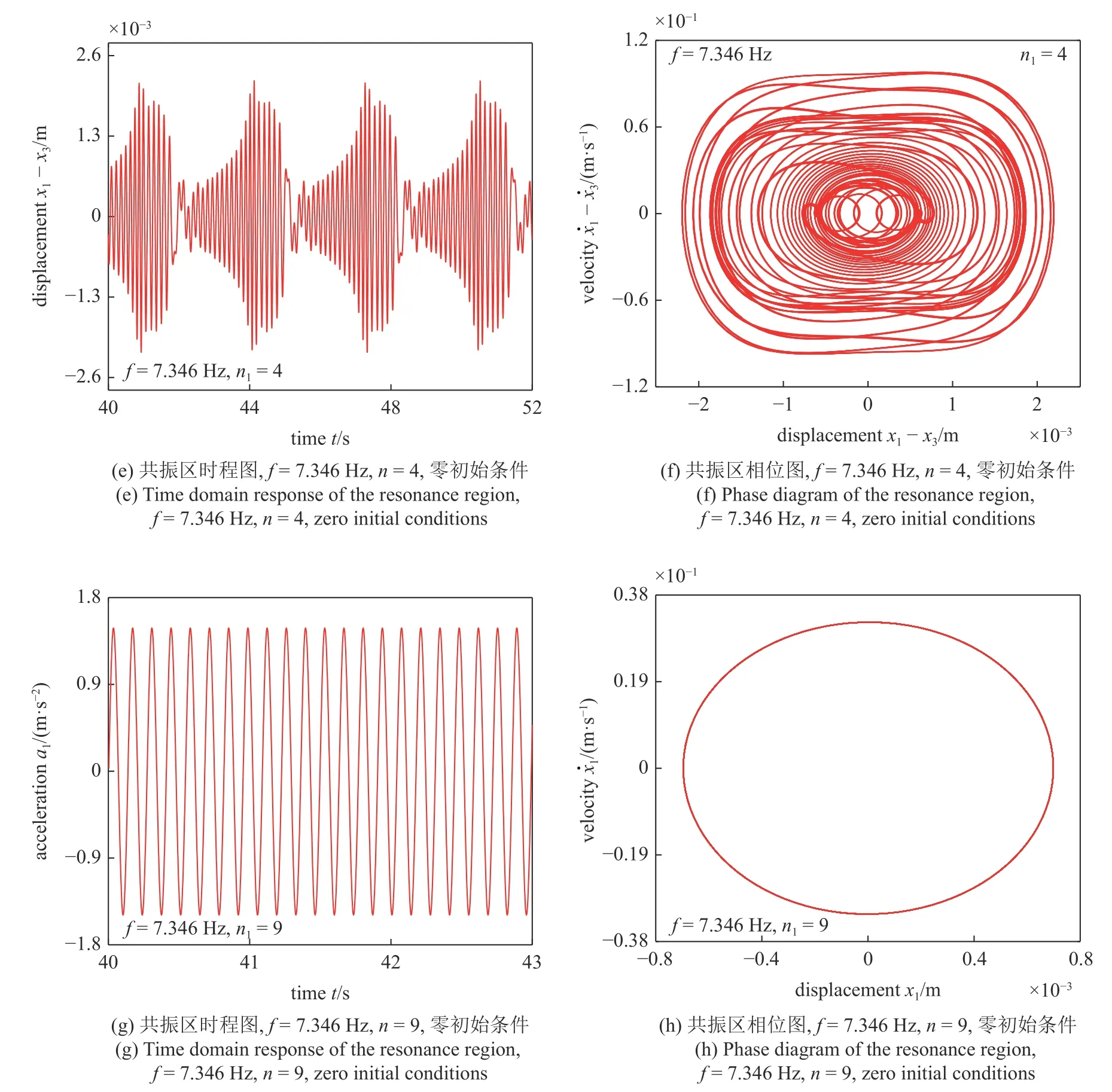
图4 共振区的时程图与相位图 (续)Fig.4 Time domain response and phase diagram of the resonance region (continued)
在图2(c)所示的情况中,单个NES 胞元的减振效率很低,对应的幅频曲线共振峰较高,形成了减振恶化区.而此时,在共振区中f=7.346 Hz 的位置,系统的响应为稳定状态,如图4(a)所示.当胞元个数增加时,共振区的稳定相应变为不稳定响应.当NES胞元增加至2 时,系统就处于强调制响应状态了,如图4(c)和图4(d)所示.此时主振子的能量以不可逆转的方式靶向传递至NES 胞元中.而为了更好地展现强调制响应状态,在图4(c)~图4(f)中,采用主振子与NES 胞元的位移差及速度差来衡量其运动.当胞元个数继续增加时,系统的强调制响应幅值减小.这一点可以通过对比图4(d)和图4(f)得出.当胞元个数从2 增加至4 时,主振子与NES 胞元位移差的幅值减小.而当胞元个数继续增加时,系统的响应又从强调制响应变为稳定响应.当胞元个数增加至9 时,系统的响应就已经变为稳定响应了,如图4(g)和图4(h)所示.
根据上述分析,可以总结出胞元个数对共振区响应状态的一般规律:随着胞元个数的增加,共振区响应从稳定响应转变为强调制响应,最后又变回稳定响应,而响应处于强调制状态时,其幅值随着胞元个数的增加而减小.从能量的角度看,胞元个数的增加会使得主系统传递至每个NES 胞元的能量减小,进而减轻了单个胞元的压力,因此强调制响应的幅值会随着胞元个数增加而持续减小,直至响应呈现出稳定状态.而在整个过程中,胞元个数的增加一般会使胞元减振效率提升.
4 结论
本文对NES 胞元的减振效率进行了理论分析.将不同个数的两种重量NES 分别耦合于线性振子上,在偏心转子激励的情况下,采用复化平均法和龙格-库塔法探究了NES 胞元的减振效果及系统响应规律.得出的结论包括:NES 能够以胞元的形式方便地应用于振动结构的控制,而且增加NES 胞元的个数会显著增加NES 对主结构的减振效果,且振子重量大的NES 胞元具有更好的减振效果.尤其是当小重量胞元的数量较少时,随着胞元数量的增加,减振效率会快速增长.胞元个数的增加会使得系统共振区响应状态从稳定状态、强调制状态到稳定状态依次变化.其中,强调制响应的幅度随着胞元个数增加而减小.
本文提出了一种可以使NES 便捷高效地应用于工程减振的策略,即将NES 胞元化装配于主结构中.此外,通过理论分析NES 胞元的减振规律,揭示了其减振潜能.未来,将对NES 胞元的结构进行研究和设计,使其更加可靠和高效,并研究NES 胞元在不同主结构中的应用,为NES 应用于工程减振奠定基础.
