基于闭环控制的齿轮传递误差研究

杨振虎

(山东劳动职业技术学院智能制造系，山东 济南 250300)

闭环齿轮传动系统是当前工业制造机器中经常用到的机械传动系统，当系统出现齿轮传递误差时，会立刻改变齿轮的传动比，导致系统噪声增大，对系统的传动平稳性产生消极影响[1]。因此研究闭环齿轮传动系统的齿轮传递误差十分重要。经过实际调查分析发现，闭环齿轮传动过程中振动和噪声的主要来源是齿轮传递误差，因此大量学者开始研究齿轮传递误差。文献[2]提出基于齿轮啮合质量的传递误差问题，还分析了齿距啮合偏差对齿轮传递误差的影响程度，但没有从闭环齿轮传动系统角度出发研究齿轮传递误差。文献[3]提出基于误差耦合补偿的齿轮传动误差问题，能够有效降低传动误差，但未考虑齿轮同步传递误差。

针对上述研究存在的问题，笔者从当量啮合传递误差角度出发，研究闭环齿轮传动系统中的齿轮传递误差，最终依照位置环误差控制方法调节误差初始相位，降低齿轮同步传递误差，提升闭环齿轮传动系统的平稳性。

1 当量啮合传递误差分析

1.1 当量啮合传递误差参数计算

当量啮合误差是一种等效误差，主要由安装误差和齿轮制造误差引起，当量啮合误差啮合线的延长方向为正方向，反之为负方向。图1为当量啮合误差图。

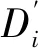
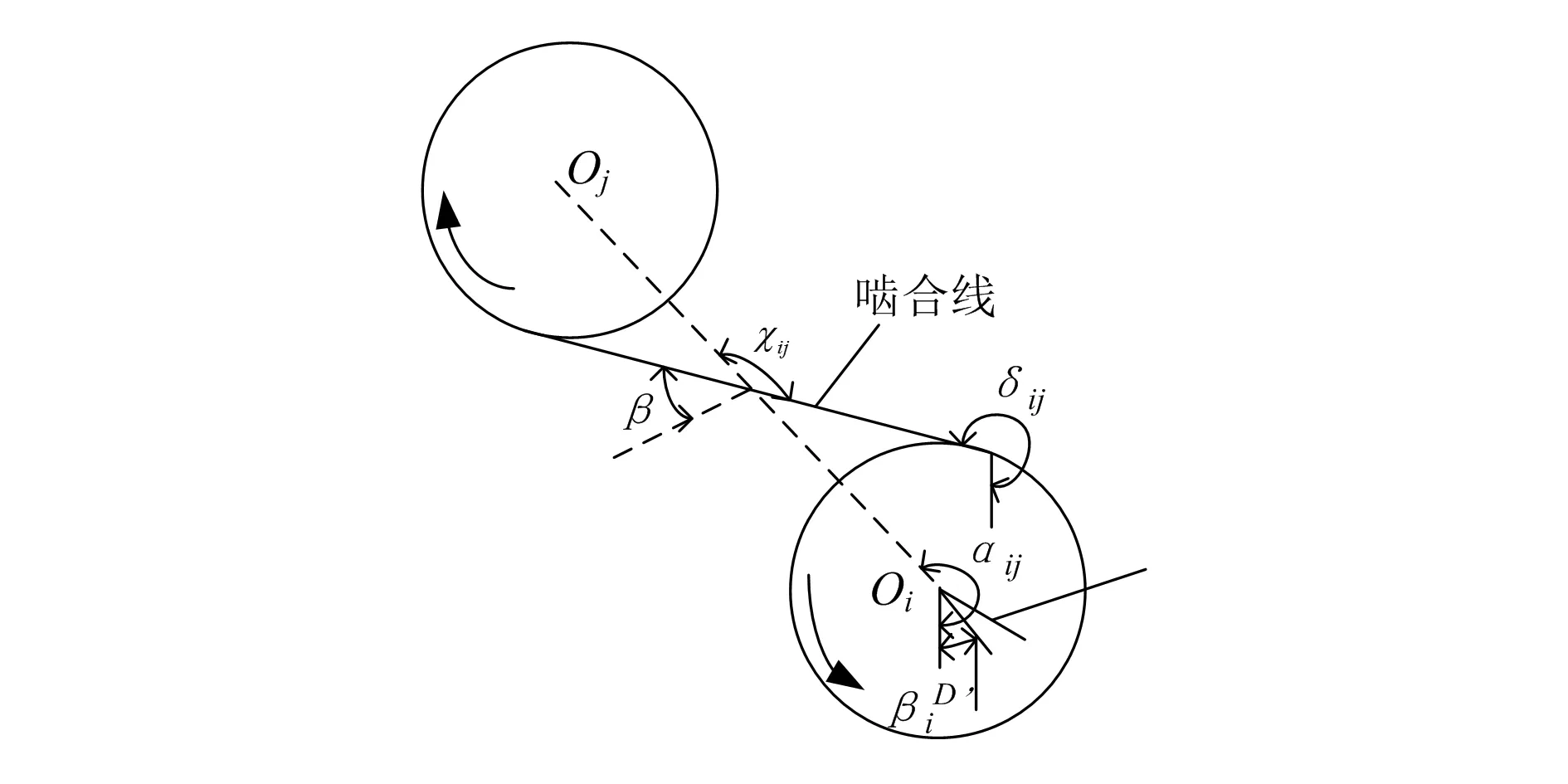
图1 当量啮合误差图

(1)

(2)

式中：b为齿数。

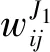
(3)

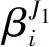
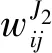
(4)

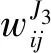
(5)

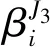
假设啮合线上存在齿轮安装误差wAij和制造误差wZij的投影，可得到：

(6)

整个闭环齿轮传动系统结构如图2所示。

图2 闭环齿轮传动系统结构图

从图中可看出，该闭环齿轮系统中包含m个齿轮组，m≥2，且m是偶数。闭环齿轮系统中功率分流成Z1和Z2两个支路。αij(Z1)、αji(Z1)、αij(Z2)、αji(Z2)分别为当传动方向为ij时x轴和传动方向之间不同的夹角，χij(Z1)、χji(Z1)、χij(Z2)和χji(Z2)分别为当传动方向为ij时x轴和啮合线之间不同的夹角。相关角度的计算公式如下：

(7)

(8)

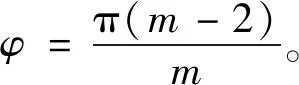
1.2 当量啮合传递误差计算

理论转角和实际转角之间的差值为齿轮传递误差，当差值为正数时，理论转角小于实际转角，反之大于实际转角。设闭环齿轮系统逆时针旋转为正向，顺时针旋转为负向。此系统中齿轮安装误差和制造误差构成单个齿轮误差，单个齿轮误差Pi计算公式如下：

Pi=wAij+wZij

(9)

同时综合相互啮合的单个齿轮误差得到一对齿轮副的误差，该误差计算公式如下：

(10)

式中：δ1为齿轮副的误差；P1和P2分别为齿轮1和齿轮2的误差；r2为齿轮2的基圆半径。通过传动比将多个齿轮副误差转化到最后一个齿轮上得到齿轮传递误差[3]，误差δ计算公式如下：

(11)

式中：δm为第m个对齿轮副传递误差；im-1为第(m-2)根轴到第(m-1)根轴的传动比。

2 同步传递误差计算

闭环齿轮传动系统中，输入轴的额定功率在第一个齿轮处将功率分流成两个支路传递，两个支路传递的功率在最后一个齿轮上汇合。传递过程中该系统会出现噪声：一种是开环传动过程中支路传递误差导致的，另一种是功率合流时齿轮传动不同步导致的。齿轮传递误差仅能反映各个支路中单独齿轮的准确性和平稳性[4]，为研究整个系统的平稳性，需考虑齿轮的同步传递误差,通过同步传递误差可以反映多输入齿轮传动时齿轮的同步性。同步传递误差指整个齿轮传动过程中，当单个齿轮接收到多个主动齿轮传递的功率时，两种齿轮之间传递误差的差值[5]，公式表示为：

T=δZ1-δZ2

(12)

式中：T为同步传递误差；δZ1和δZ2分别为Z1和Z2两个支路的传递误差。通过上述计算获取了闭环齿轮传动系统中齿轮传递误差后[6]，应采用位置控制方法控制闭环齿轮传动系统中的齿轮传递误差，减少齿轮传动过程中出现的角度和位移偏移。

3 基于位置环PID的误差控制方法

为实现对闭环齿轮传动系统中齿轮传递误差的控制，需采用位置环限定传动过程中齿轮的位移和角度，改变齿轮误差初始相位。本文设计的位置环整体结构如图3所示。

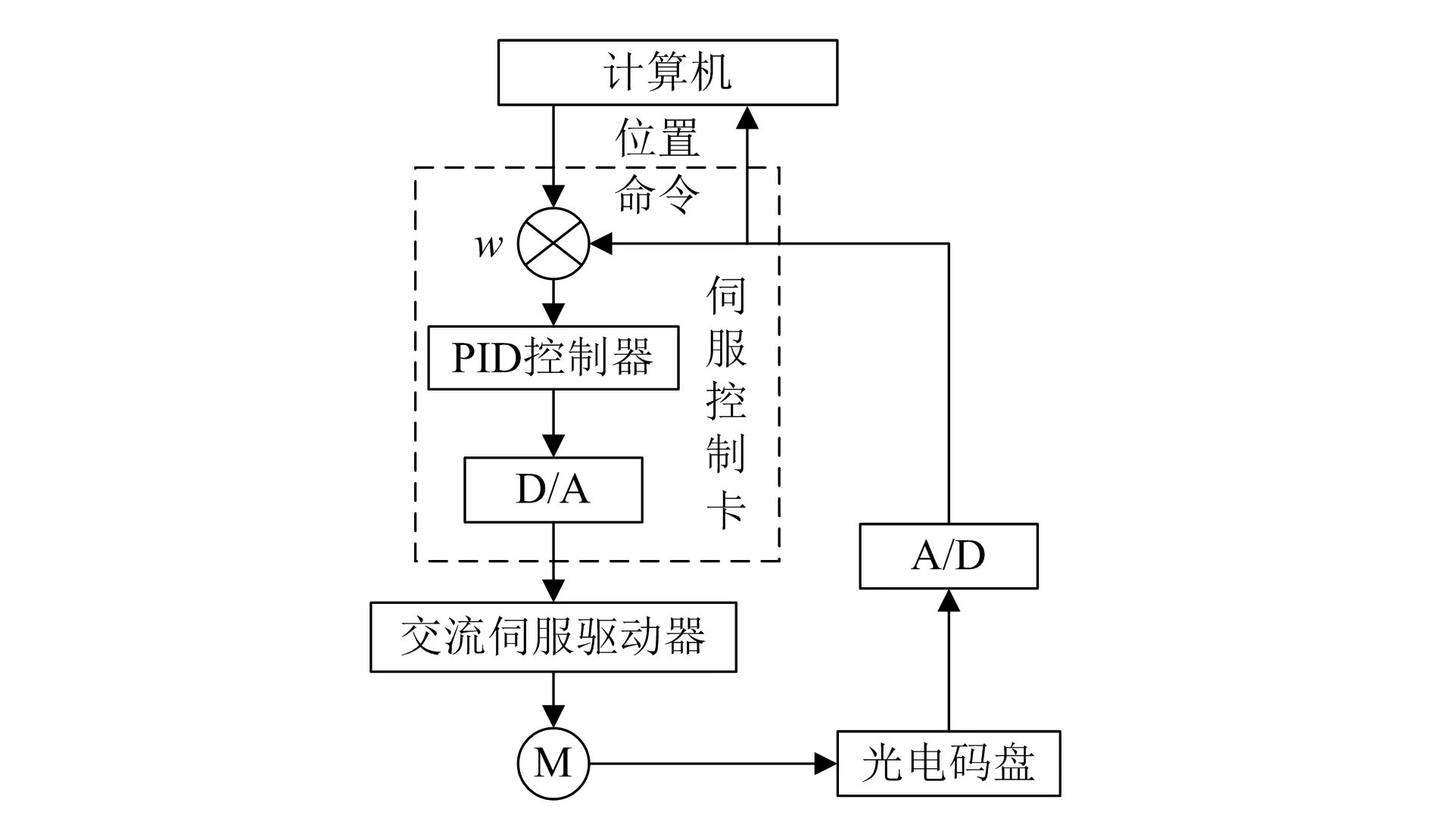
图3 位置环整体结构

从图可知，该位置环主要包含计算机、PID控制器、交流伺服驱动电机(M)等部分。在齿轮传动过程中，应采用光电码盘将齿轮位置变换量转换成相差分脉冲，并将其传输到计算机中对脉冲进行计数，向PID控制器提供反馈信号，如此就实现了位置反馈。采用脉冲计数获取数字化信息位置，根据计算机计算反馈位置和实际位置之间的偏差数值，采用相应的PID控制策略[7]，经过D/A转换成模拟控制电压并传输到交流伺服驱动机中，调节交流伺服驱动机的运转情况，最终完成期望值的定位，实现对齿轮传递误差的修正。

在闭环齿轮传动系统中，为调节传递误差，需设置一定的PID参数，但是如果整个过程中多次设置参数[8]，会引起系统的超调和震荡。为减少上述情况，PID控制过程中需采用积分分离的PID控制算法，当齿轮传递既定位置大于齿轮传递实际位置和齿轮传递期望位置之间差值时，恢复积分校正环节[9]，降低系统稳态误差，提升控制精准度。

采用积分分离的PID算法时需设定积分分离阈值ε，比较ε和实际误差，当ε和实际误差具有较大差异性时，需要采用PID算法对ε进行调整。离散化的PID控制算法公式如下：

(13)

式中：W(l)为位置控制量，其中l为采样序号，l=0,1,2,…；lp为比例系数；li为积分系数；ld为微分系数[10]。

通过式(13)计算出齿轮传动过程中齿轮传递位置控制量，即可依照该位置控制量调整闭环齿轮传动系统中齿轮误差初始相位，降低齿轮传动过程中产生的传递误差值和齿轮磨损程度。

4 实验方法测试

为验证该方法的有效性，需进行实验检测。实验选择由6个齿轮组成的闭环齿轮传动系统在某工厂内进行实际应用，实验选用的减速器中心距为155 mm；齿轮的传动比为3，齿轮齿数为8，齿面宽20 mm；动力采用直流电机，电机的额定功率为40 kW,额定转速为3 500 r/min。齿轮的材料为合金钢，弹性模量为207 000 MPa，泊松比为0.35。在闭环齿轮传动系统中，输入功率会在齿轮S1处分流，在S4处进行功率合流，输入功率是通过两条相对独立的支路进行传递的，即支路Z1(S1(Z1),S2(Z1),S3(Z1),S4(Z1))和支路Z2(S1(Z2),S2(Z2),S3(Z2),S4(Z2))。将闭环齿轮传动系统中齿轮的齿数设置为75，将压力角设置为21°，传动比设置为1，统计误差初始相位，结果见表1。

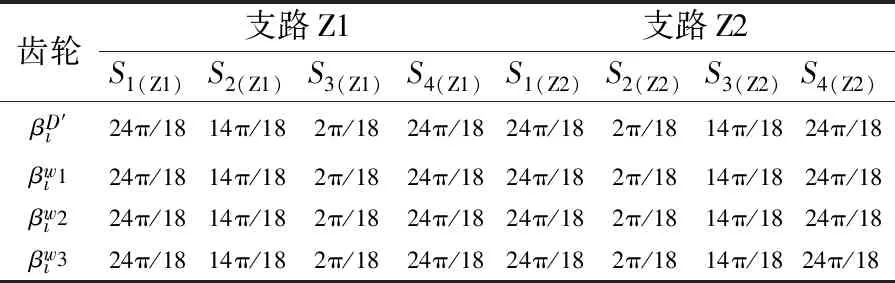
表1 误差初始相位

实际检验过程中应通过误差初始相位研究齿轮传递误差和同步误差，探析传递误差和同步误差的特点，同时检测本文方法的控制效果。

4.1 实际控制效果分析

为验证本文方法对闭环齿轮传动系统中齿轮传递误差控制效果，系统中两个支路分别采用本文方法和传统方法控制齿轮传递误差，探析在相同工况条件下6个月后两个支路中齿轮的实际控制效果，结果如图4所示。

从图中可以看出，用本文方法控制控制的齿轮未出现显著磨损，而用传统方法控制的齿轮磨损程度较为严重，对比结果证明本文方法效果较好。

4.2 当量啮合传递误差和同步误差特点

为研究当量啮合传递误差和同步误差与时间的关系，需采用本文方法分析当量啮合传递误差和同步传递误差特点，在实验工况条件下的结果如图5所示。

图4 实际效果图

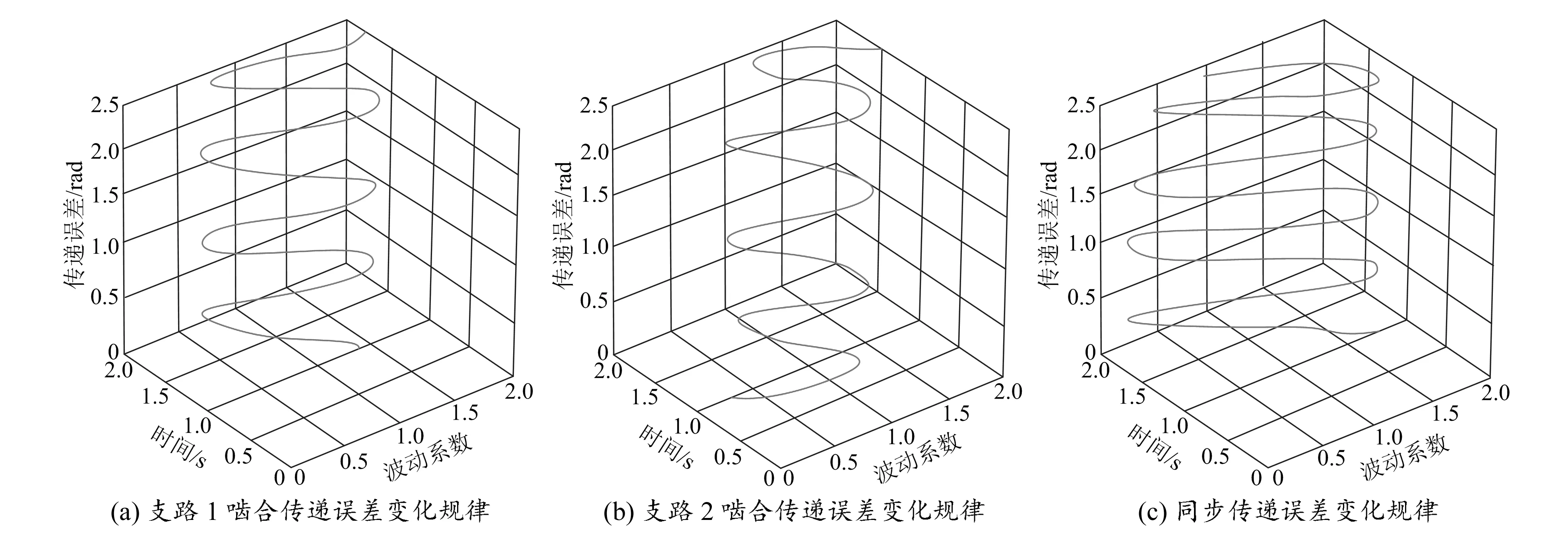
图5 传递误差变化规律

从图可知，两个支路齿轮传递误差都以高频和低频随时间呈周期性变化，同时可以看出两个支路齿轮传递误差不同步，且两个支路齿轮传递误差中的最大瞬时传递误差不一致，对比发现，同步传递误差中存在耦合作用，因此采用位置环误差控制方法控制齿轮传递误差。

4.3 控制结果

本文通过PID控制算法调节齿轮切向误差初始相位，实现对闭环传动系统中的齿轮传递误差的调节，控制后的误差初始相位见表2，控制后的同步传递误差变化规律如图6所示。

表2 控制后各误差初始相位

从表2中可以看出，使用本文方法控制闭环齿轮传动系统后，系统中各个齿轮误差初始相位相差0或者是π，各个齿轮之间传递误差耦合情况较好，同时从图6中可以看出，采用本文方法控制后齿轮同步传递误差为0.151 8 rad，与控制前相比，同步传递误差降低到98.69%，说明本文方法效果较好。

图6 齿轮同步传递误差变化规律

4.4 本文方法稳定性

为验证本文方法的稳定性，需选取不同齿长和齿高方向的采样点，分别选取9个和5个，检测采用本文方法控制后系统中齿轮凸面和凹面法向偏差，检测结果见表3和表4。

从表3和表4可以看出，经过本文方法控制后齿轮最大法向偏差绝对值是0.023 6 mm，且整个系统中各个齿轮齿面偏差变化较为均匀，说明该方法稳定性较好。

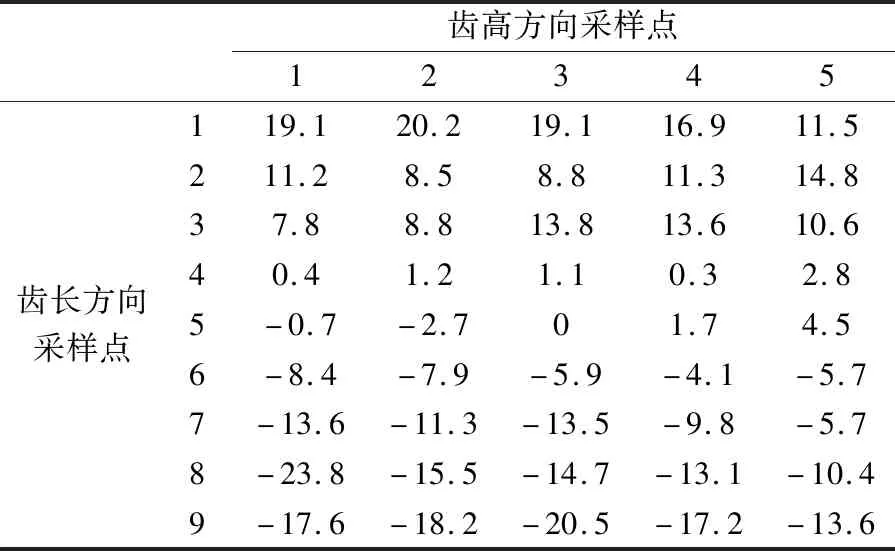
表3 齿轮法向偏差(凹面) μm

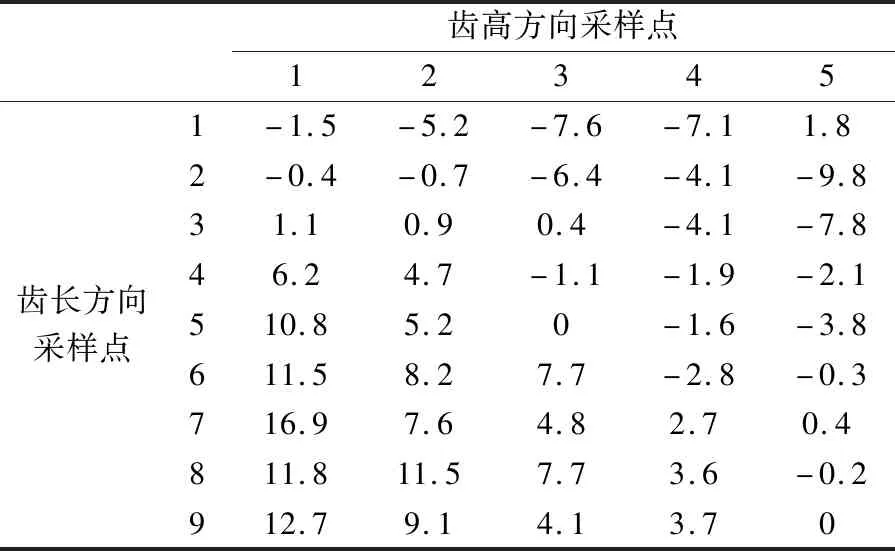
表4 齿轮法向偏差(凸面) μm

5 结束语

本文研究基于闭环控制的齿轮传递误差，实验选取包含六个齿轮的闭环齿轮传动系统为研究对象，证明了本文方法能够有效控制齿轮传递误差，控制稳定性较好。原因在于该方法在分析当量啮合传递误差、安装误差和制造误差、同步传递误差的基础上，采用位置环PID控制方法计算齿轮传递位置控制量，实现基于闭环控制的齿轮传递误差控制方法。采用该方法能够减小齿轮传递误差与噪声，提升系统的稳定性，提高制造效率，促进综合效益的大幅度提升。