侵彻过程数值模拟单元及网格的试验研究

王玉凯，赵建新，韩国柱

(中国人民解放军陆军工程大学石家庄校区火炮工程系，河北 石家庄 050003)

目前，针对各种侵彻问题一般采用有限元法进行解决。单元和网格作为有限元方法的基础，对数值计算的规模、精度等有不可忽视的影响，为了得到客观、理想的仿真计算结果，研究人员需要分析其变化对仿真结果的影响程度。门建兵等[1]通过对比不同尺寸网格的数值计算结果，分析了单元尺寸对混凝土侵彻数值模拟的影响，获得了较为合理的网格尺寸。邓记松[2]通过模拟研究了压力容器的应力分析设计，明确了单元类型、单元技术和网格密度对有限元分析结果有直接影响。林华令等[3]采用拉格朗日网格描述法对混凝土侵彻问题进行了数值模拟分析，考察了拉伸失效模式、网格尺寸和销蚀应变对模拟结果的影响，得到的结论是网格尺寸为5.0 mm时较为合适。

为保证仿真模拟结果的客观性，排除人为设定因素的影响，本文利用ABAQUS软件对枪弹侵彻松木靶板过程进行仿真模拟，探究单元类型和网格尺寸对仿真模拟结果的影响，明确了适用于枪弹侵彻过程仿真模拟的单元类型和网格尺寸。

1 数值模拟

1.1 模型构建

弹、靶几何结构及其所受载荷具有明显的轴对称性，建模时可只构建1/4弹、靶的仿真模型，以便于仿真模型的建立和减少计算量。为了模拟真实情况，由弹头壳、铅套和弹芯三部分组成的弹头模型参照7.62 mm枪弹弹头建成，如图1所示。同时，构建尺寸为250 mm×100 mm×25 mm的松木靶板1/4板模型，其材料参数可通过查阅含水量为12%左右的俄罗斯红松木的资料获得[4]。根据弹、靶材料力学性能及特点，分别采用Johnson-Cook模型和改进的Hashin失效模型来描述弹丸和靶板的动态力学响应。为更准确地描述枪弹侵彻靶板的损伤破坏过程，选择面面侵蚀接触来处理枪弹与靶板的接触问题。

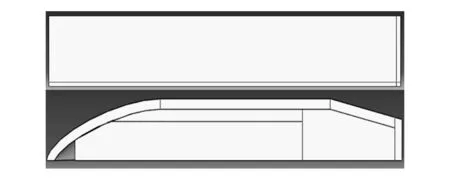
图1 枪弹和靶板几何形状

1.2 单元类型

ABAQUS/EXPLICIT中有丰富的实体单元库，针对不同的问题可以选择不同的单元类型进行解决。对于三维动力学问题，六面体单元和四面体单元是两种应用较为广泛的单元类型。由于枪弹侵彻松木靶板属于动态力学大变形问题，弹、靶在高速撞击侵彻过程中均发生损伤变形，而松木靶板的几何构型为规则的长方体，因此为了便于对靶板进行网格划分，节约计算成本以及保证计算准确性，分别选择三维线性六面体单元C3D8R和三维修正四面体单元C3D10M作为靶板的单元类型[5]。

C3D8R单元(图2(a))是线性六面体减缩积分单元，包含8个节点，每个节点有6个自由度，分别为沿x,y,z轴向的平移和绕各个轴的转动。C3D8R单元形状规则，具有一定的承受扭曲变形的能力，可以根据需要设定扭曲控制的长度比来减少单元扭曲变形的影响，划分出的靶板网格质量较高。但是该单元本身存在沙漏数值问题，需要通过“沙漏控制”设定“沙漏刚度”来增加单元的刚度，控制沙漏在模型内的扩展。在枪弹侵彻松木靶板过程的仿真模拟中，靶板单元会发生严重的扭曲变形，为避免单元扭曲对计算结果的影响，需将扭曲控制的长度比设定为0.1。其多项式位移模式为：

u=a1+a2x+a3y+a4z+a5xy+a6yz+a7xz+a8xyz

(1)

v=b1+b2x+b3y+b4z+b5xy+b6yz+b7xz+b8xyz

(2)

w=c1+c2x+c3y+c4z+c5xy+c6yz+c7xz+c8xyz

(3)

式中：u为x方向的节点位移函数；v为y方向的节点位移函数；w为z方向的节点位移函数；ai为x方向节点位移函数的插值多项式系数；bi为y方向节点位移函数的插值多项式系数；ci为z方向节点位移函数的插值多项式系数；x,y,z为整体坐标。

自然坐标系的形函数为：

(4)

式中：Ni为形函数；ξ0=ξiξ,η0=ηiη,ζ0=ζiζ，其中ξ,η,ζ为自然坐标，ξi,ηi,ζi为节点i的自然坐标。

C3D10M单元(图2(b))是修正四面体单元，包含10个节点，各节点的自由度与C3D8R单元相同。该单元同样需要考虑单元扭曲的影响，设定合理的扭曲控制参数，与C3D8R单元不同的是,该单元本身能够较好地解决沙漏数值问题，不需要通过设定沙漏控制参数来解决仿真过程中沙漏的影响。10节点四面体单元的多项式位移模式为：

u=a1+a2x+a3y+a4z+a5xy+a6yz+a7xz+a8x2+a9y2+a10z2

(5)

v=b1+b2x+b3y+b4z+b5xy+b6yz+b7xz+b8x2+b9y2+b10z2

(6)

w=c1+c2x+c3y+c4z+c5xy+c6yz+c7xz+c8x2+c9y2+c10z2

(7)

自然坐标系的形函数为

Ni=(2Li-1)Li(i=1,2,3,4)

N5=4L1L2

N6=4L2L3

N7=4L1L3

N8=4L4L1

N9=4L4L2

N10=4L4L3

式中：Li为第i节点单元的面积坐标。

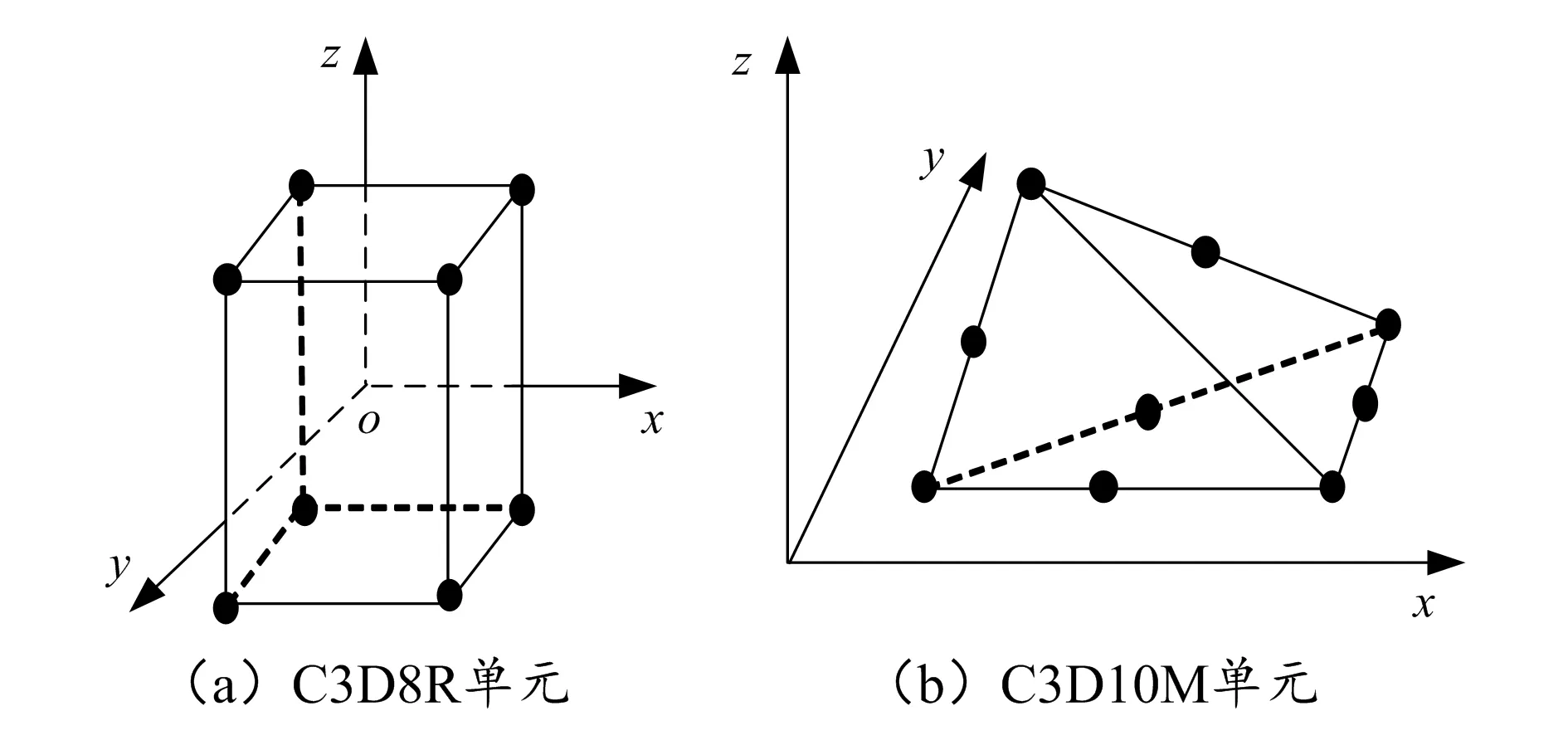
图2 靶板模型单元类型

根据上述两单元的多项式位移模式和自然坐标系的形函数可以发现，两单元的多项式位移插值函数阶次均比较高，由有限元相关理论可知，基于两单元的有限元计算的精度较高，整个计算收敛的速度也较快。但是，由于其阶次较高，相应的计算量也会比较大，因此运算过程中计算精度与计算量需要平衡好。

1.3 网格划分

由于Zukas等[6]对网格划分的研究结果表明弹丸半径方向上的网格数应不少于3个，因此本文中弹丸半径上的网格数划定为4个。考虑到靶板实际的损伤情况以及计算量，基于Lagrange法应用局部网格加密的方法对弹靶接触区域进行局部网格细化，而其他区域的网格尺寸则相对较大[7-9]，如图3所示，其中网格细化的范围为20 mm×20 mm。另外，为了便于操作，设定靶板厚度方向的网格尺寸为1 mm，网格数量始终为25，其他两个方向的网格尺寸相同[10-11]，根据需要分别设定为1.00 mm、1.30 mm、4.00 mm、6.67 mm。分别对这4种尺寸的网格进行计算，综合分析比较其计算结果，找到最合适的网格尺寸。靶板细化区域划分的网格尺寸与单元数量见表1。

图3 松木靶板模型网格划分情况

表1 靶板细化区域网格尺寸和数量

2 计算结果

2.1 单元类型的影响

图4所示分别为两种不同的单元类型模拟得到的弹丸速度随时间变化的曲线。由图可以看出，不同单元类型模拟得到的弹丸速度衰减过程以及着弹时弹丸剩余速度是不同的。C3D8R单元模拟得到的弹丸速度变化是逐步衰减至剩余速度为697.0 m/s，而C3D10M单元模拟得到的弹丸速度变化是突然衰减至剩余速度为675.0 m/s，然后在该值上下波动。C3D8R单元模拟得到的弹丸剩余速度值与实验值698.8 m/s几乎一致，相差仅为1.8 m/s，而C3D10M单元模拟得到的弹丸剩余速度与实验值相差23.8 m/s。综上所述，单元类型对于枪弹侵彻松木靶仿真结果具有重要影响，C3D8R单元是较为合适的单元类型。

图4 不同单元类型的弹丸速度-时间曲线

2.2 网格尺寸的影响

在分析使用不同网格尺寸模拟弹丸速度-时间曲线(图5)时发现，仿真得到的4条速度-时间曲线非常相似，且弹丸着弹时剩余速度也相差不大，网格尺寸为1.00,1.30,4.00,6.67 mm分别对应的弹丸剩余速度为 697.0,699.6,696.0和695.2 m/s。图5显示除了网格尺寸为1.30 mm外，当网格尺寸由1.00 mm增加至6.67 mm时，仿真得到的弹丸剩余速度随网格尺寸的增加而减小，但衰减幅度却随之增大。当网格尺寸为1.30 mm时，仿真得到的弹丸剩余速度与实验值698.8 m/s更加接近。图6所示为4种网格尺寸的靶板模型模拟的靶板损伤情况，分析发现，网格尺寸为1.00 mm和1. 30 mm时模拟的靶板损伤情况比网格尺寸为4.00 mm和6.67 mm时更加精细，弹孔的形状与实际也更加接近。

图5 不同网格尺寸的弹丸速度-时间曲线

图6 靶板的损伤情况

3 结论

本文通过对7.62 mm枪弹侵彻松木靶过程进行仿真模拟，分析了单元类型和网格尺寸对仿真结果的影响，得到如下结论：

1)运用 C3D8R单元划分网格的单元数量明显少于C3D10M单元，表明模拟仿真时的计算量小于C3D10M单元。利用C3D8R单元进行网格划分时，模拟获得的弹丸剩余速度与实验结果更加接近。

2)单元类型一定时，仿真模拟的弹丸剩余速度和靶板损伤情况随着网格尺寸的变化而变化。网格尺寸为4.00 mm和6.67 mm时模拟的结果与实际值差别较大，网格尺寸为1.00 mm和 1.30 mm时模拟的靶板损伤情况与实际情况很接近，且网格尺寸为1.30 mm时模拟的弹丸剩余速度值更加接近实际值。

3)为了得到理想的仿真结果，较为合理的建模设定是C3D8R单元和1.30 mm的网格尺寸。