飞机复合材料阶梯状蒙皮有限元建模方法研究

杨晓东

(上海飞机设计研究院，上海 201210)

飞机自然网格有限元模型以飞机结构骨架数模(机身按框/长桁，翼面按肋/长桁)作为网格划分标准，反映飞机结构主承力构件的传力特征，是飞机结构强度设计、分析的主要依据和基础[1-2]。

复合材料在航空领域的使用已越来越普及，现今复合材料的使用率已经成为飞机先进性的评判标准之一。复合材料结构复杂，给飞机蒙皮的有限元建模及分析带来很多挑战。比如，有的结构铺层变化剧烈，呈阶梯状。而在自然网格下，长桁间或框/肋间通常只有一个规则的板壳单元，无法反映阶梯状的铺层变化。

因此本文提出一种新的建模方法，以求能够保证等效后的变形与实际结构变形相近。具体思路为：第一步，按阶梯边界把单元分块，求解出每一块综合的刚度矩阵；第二步，考察整个单元在单向拉压和纯剪切作用下的变形，在一定假设下，求出4个等效刚度；第三步，用一个新的0°铺层来代替原单元，合理设置4个独立弹性常数E1,E2,υ12,G12，使得等效后的4个刚度与实际值相同。

1 理论推导

1.1 标准层压板理论

层压板板长为l，宽为b，单层厚为h，共有n层，x方向为沿长度方向，y方向为沿宽度方向，如图1所示。

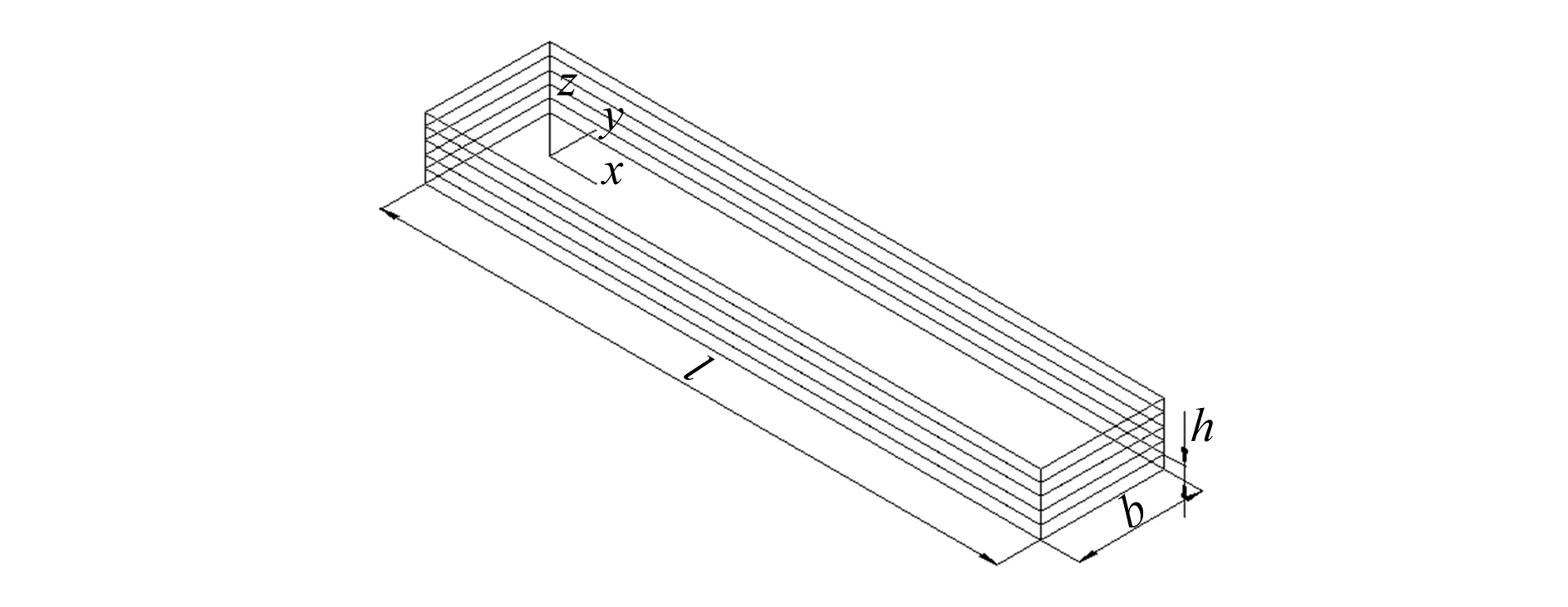
图1 典型复合材料层压板示意图

每一层都应满足式(1)：

(1)

式中：σx和σy分别为任意正交x和y方向正应力；

τxy为xy平面内剪应力；εx和εy分别为对应x和y方向正应变；γxy为xy平面内剪应变；下标1，2分别表示纤维方向和垂直于纤维方向；E1,E2分别为1方向和2方向的弹性模量；υ12为当在1方向受拉伸时决定2方向收缩量的泊松比；υ21为当在2方向受拉伸时决定1方向收缩量的泊松比；G12为面内剪切模量；c为纤维方向与x方向夹角的余弦值；s为纤维方向与x方向夹角的正弦值。

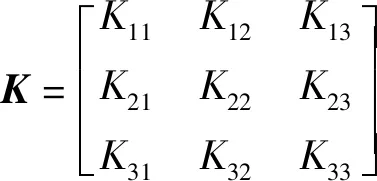
(2)

式中Kij可由式(1)对应位置求出。

假设层压板单层内应力应变与z坐标无关，并且不同层间的同一个(x,y)坐标点具有相同的位移和应变。

定义应力合力：

(3)

式中：Nx，Ny分别为x和y方向的正应力合力;Ns为剪应力合力；p为铺层序号。

将式(3)代入式(2)得到：

(4)

同时将n层看作一个整体:

(5)

对比式(4)、式(5)得到层压板的刚度矩阵各分量Kij满足：

(6)

而对于不等厚的层压板，各分量容易证明满足

当铺层对称，并且均衡(对于不为0°或90°的角度θ，每有一个θ的铺层就对应存在一个-θ的铺层)时，层压板刚度矩阵分量K13,K23,K31,K32均为0，即拉压和剪切解耦[4]。

1.2 阶梯状层压板理论推导

1.2.1刚度定义

如图2所示，单元按阶梯边界可分为n块，从左至右依次为第1,2,…,n块。考虑掉层后仍满足对称以及±θ角度对应铺层，则可以将每一块等效为一层后再进行计算。

图2 阶梯状层压板示意图

对刚度矩阵K取逆，得到柔度矩阵λ。

(7)

式中：λmn为相应柔度系数。

结合式(2)得到

(8)

对于某一块，有

(9)

对刚度作如下定义：

(10)

式中：kx,ky分别为x,y方向单向拉伸刚度；kxy,kγ分别为xy方向耦合刚度及剪切刚度。

1.2.2x方向单向拉压响应

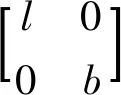
(11)

式中：Δl，Δb分别为长度和宽度方向的变化量。

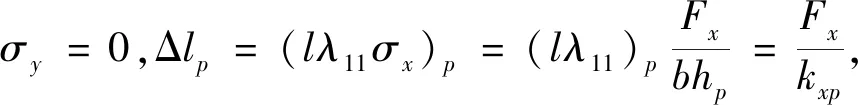
(12)

现假设整个单元在y方向变形是一致的，位移为Δb，因此在受到拉力Fx作用的同时，还存在y方向的自平衡力系，设第p块上受到y方向的拉力为F0p,整个单元上F0p合力为0。

对于整个单元：

(13)

1.2.3y方向单向拉压响应

考虑到y方向变形一致，则每一块阶梯状层压板都承受y方向的拉力。

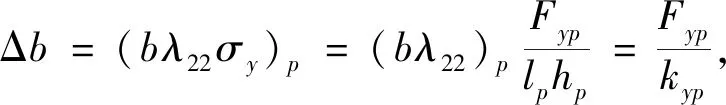
(14)

式中：Fyp为第p块y方向拉力。

1.2.4纯剪切响应

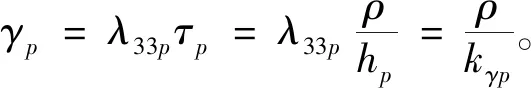
(15)

对其变形可得：

(16)

1.3 等效常数确定

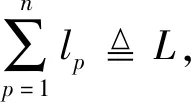
(17)

2 建模验证

2.1 建模及参数计算

建模及仿真计算采用ABAQUS 6.11软件。设置材料为碳/环氧树脂，材料常数为E1=137.44 GPa，E2=11.71 GPa,υ12=0.25，υ21=0.021 3，G12=5.51 GPa。

复合材料层压板共铺12层，每层厚度0.2 mm，长度为80 cm，宽度为30 cm，其中0°铺2层，45°铺4层，-45°铺4层，90°铺2层，满足对称铺层的要求。层压板右侧有20 cm长度区域设置4层掉层，分别为45°2层，-45°2层，不掉层和掉层区域长度分别为60 cm和20 cm。

按照第1节中的计算过程，求得等效材料常数为E1=42.206 GPa，E2=42.568 GPa，υ12=0.392 4，G12=21.241 GPa。

2.2 不同工况加载对比

2.2.1x方向单向受拉载荷

约束左下角节点x,y方向位移和左边线节点x方向位移，并在右边线节点的x方向上施加3 000 N/m的拉力。仿真得到的实际结构x方向位移云图如图3所示，等效处理后，约束和加载情况不变，得到的位移云图如图4所示。

图3 等效处理前x方向位移云图(x单向受拉)

图4 等效处理后x方向位移云图(x单向受拉)

2.2.2y方向单向受拉载荷

y方向单向受拉载荷和x方向类似，约束左下角节点x,y方向位移和下边线节点y方向位移，在单元的y方向边界上施加3 000 N/m的拉力,得到的实际结构位移云图如图5所示。等效处理后，约束和加载情况不变，得到的位移云图如图6所示。

图5 等效处理前y方向位移云图(y单向受拉)

图6 等效处理后y方向位移云图(y单向受拉)

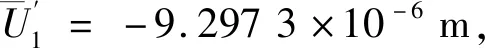
2.2.3纯剪切载荷

约束左下角节点x,y方向位移和下边线未丢层60 cm区域y方向位移，在层压板四边施加3 000 N/m的剪力。得到的实际结构位移云图如图7所示。等效处理后，约束左下角节点x,y方向位移和右下角节点y方向位移，单元四边加载3 000 N/m的剪力，得到的位移云图如图8所示。

图7 等效处理前x方向位移云图(纯剪切)

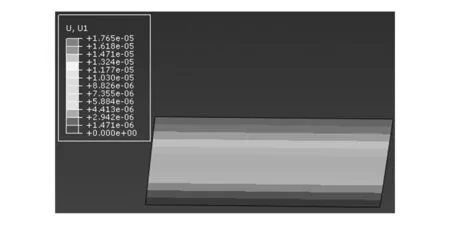
图8 等效处理后x方向位移云图(纯剪切)

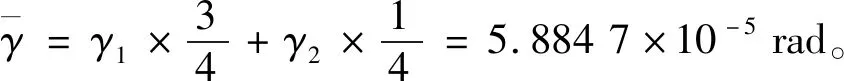
等效处理后，从场输出报告得到剪切角γ′=5.884 1×10-5rad。

2.3 结果对比分析

将不同工况下实际结构位移和等效建模计算位移列在表1中，可以看出：等效模型能够很好地模拟实际情况的拉压、剪切工况，对于文中所给的示例，误差在1%以内。

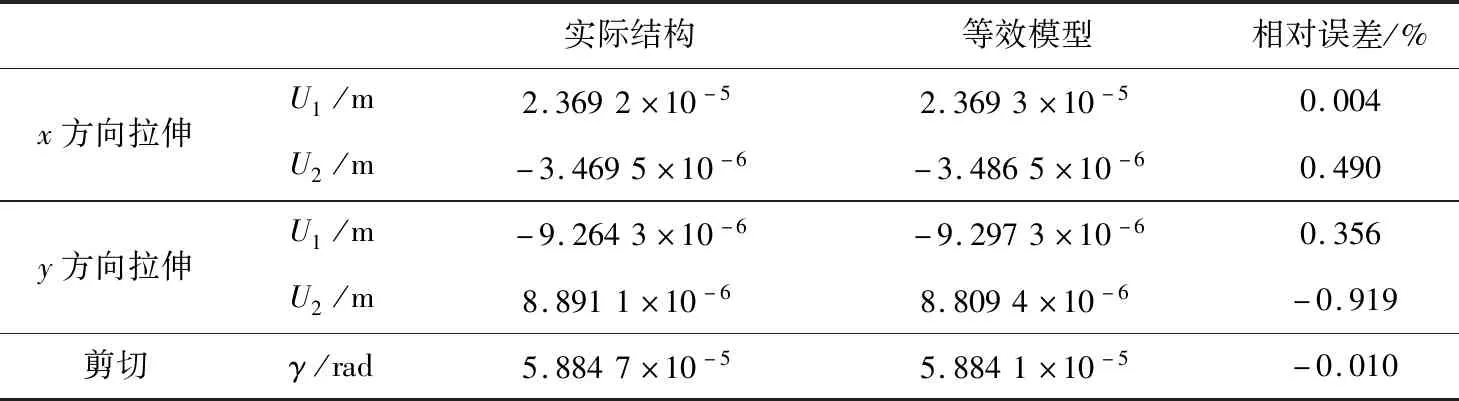
表1 不同工况下等效结果比较

3 结束语

本文通过理论推导的方式，在一定假设下，得出了复合材料阶梯状蒙皮的等效方法。通过ABAQUS软件建模仿真验证，表明该方法能够很好地模拟实际结构的拉压、剪切响应。工程实际中蒙皮主要承受拉压、剪切载荷，很少承受弯矩，因此等效方法在工程中是可行的。

同时文中分析过程也较容易退化至各向同性材料，可用于金属材料蒙皮的等效。建模时需要注意的是，等效蒙皮厚度H并没有实质上的限制，只是为了跟原几何尺寸保持一致，选取了原厚度h1。因而可以设想，通过调整等效蒙皮厚度H，在一定的假设和等效处理下，能够很好地模拟实际模型弯曲工况下的变形。因此，本文提出的建模方法对于复合材料结构有限元建模分析具有重要意义。