深埋洞室软岩开挖卸荷-流变与支护时机研究

张胜佳 许晓亮，2 赵想利 周 鑫 黄 鹏

(1.三峡库区地质灾害教育部重点实验室，湖北 宜昌 443002；2.三峡大学 土木与建筑学院， 湖北 宜昌 443002)

软岩作为一种特殊的岩体，流变持续时间比较长，常常表现出显著的大变形和非线性流变特性.岩隧道工程由于埋深大、洞程长、地质条件复杂，在修筑过程中，会发生一系列特殊的灾害地质问题，如高地应力软岩隧道在开挖过程中遇到的大变形问题[1-3]，隧洞开挖施工引起岩体应力释放并重新分布，软岩变形速率快，收敛慢，如果支护不及时或支护不当，极易发生坍塌等失稳事故[4].软岩洞室二次支护时间过早，则围岩应力释放较小，对岩体的支护要求较高，二次支护时间过晚，洞室变形过大，影响了洞室的正常使用[5].针对上述问题，国内外学者做了大量卓有成效的研究.邓华锋，方景成，李建林，等[6]对红层软岩抗压和抗拉强度特性、变形破坏特征及微观结构特征进行了比较系统的试验和检测分析.刘泉声，罗慈友，彭星新，等[7]进行软岩的现场流变试验建立了现场软弱岩体的非线性分数阶蠕变模型.R.Quevedo等[8]描述了一种可靠而有效的数值方法来预测易流变的地质材料的位移、变形和应力；陈子全，何川，吴迪，等[9]对高地应力层状软岩隧道的变形破坏机理进行了分析，提出了一种适用于高地应力层状软岩隧道的大变形预测分级指标.丁远振，谭忠盛，马栋[10]结合区域地应力、围岩强度试验等研究了高地应力断层带软岩隧道变形特征与控制措施，提出了控制大变形的技术措施.吴迪[11]研究了软岩隧道初期支护和二次衬砌的不同施作时机对围岩变形和结构受力的影响，提出了初期支护和二次衬砌施作时机的原则.

综上，目前对于软岩洞室方面的研究主要集中于：1)软岩等易流变地质材料力学特性试验研究；2)软岩变形破坏机理分析与变形预测；3)软岩洞室开挖方式选择与最佳支护时机等方面.对于软岩洞室二次支护时机的研究，特别是高地应力条件下软岩流变变形及支护的研究中较少有考虑卸荷效应的情况.为此，本文以大渡河丹巴水电站引水隧洞工程为对象，通过室内试验，开展软岩卸荷力学参数劣化分析，确定开挖卸荷、开挖卸荷-流变计算参数，借助FLAC3D模拟不同二次支护时机对深埋洞室的影响.

1 工程概况

丹巴水电站位于四川省甘孜藏族自治州丹巴县，左岸引水隧洞埋深为1000m，穿越断层破碎带，洞轴沿线出露的地层主要为志留系茂县群第四岩组(Smx4)，由灰-灰黑色蓝晶石榴二云(英)片岩、蓝晶十字石二云(英)片岩、硅线石榴二云英片岩、长英质变粒岩夹少量黑云斜长片麻岩组成.

左岸引水发电系统沿线地质构造比较复杂，断层破碎带宽约0.1～1.0m，产状为N60°W，NE∠65°，强卸荷带水平深度一般约1.8～20.0m 以内，垂直深度一般小于17.0m；弱卸荷带一般为沿顺层随机发育，水平深度一般约27.0～39.5m，垂直深度一般为28.0～37.0m.引水线路尾部区边坡强卸荷带水平深度为4.5m，弱卸荷带水平深度为45.5m，工程地质剖面图如图1所示，研究区段围岩类别属于Ⅳ(Ⅳb)类.

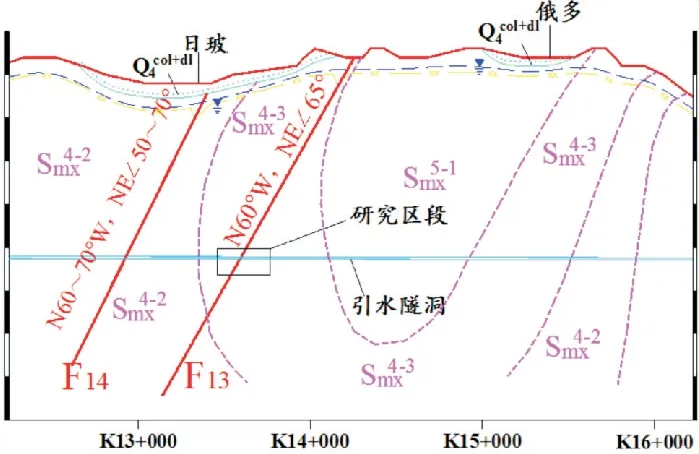
图1 工程地质剖面图

根据丹巴地质勘探资料，丹巴深埋洞室围岩初始地应力大多在25～35MPa左右，且围岩为较弱的石英云母片岩，抗压强度约为20MPa.丹巴岩体强度应力比值(R)均在4以下，属极高地应力，可见，丹巴地质条件为高地应力下的深埋软弱挤压围岩.

2 软岩卸荷力学参数劣化分析

以大渡河丹巴水电站左岸平洞的石英云母片岩为研究对象，该片岩干密度约2.65～2.85g/cm3，颜色分布不均匀，呈灰、灰白、深灰等多种颜色，中低硬度，为弱风化岩层，呈弱松弛或挤压变形状.按试验规程[12]制成标准岩样分别开展室内单轴压缩试验、不同围 压 水 平(5MPa、10 MPa、15 MPa、20 MPa、25 MPa)的三轴压缩试验和三轴卸荷试验.三轴卸荷试验的卸荷应力水平取相应围压下三轴抗压强度80%，卸荷阶段采用恒轴压卸围压控制模式，保持轴压不变，以0.05MPa/s的卸围压速率卸围压至岩样破坏.

2.1 强度参数劣化分析

由Mohr-Coulomb准则，分别得到单、三轴压缩试验和三轴卸荷试验的抗剪强度参数，见表1.同时，表1还给出了三轴卸荷试验相对于三轴压缩试验抗剪强度参数的降幅.

表1 单三轴压缩、卸荷试验抗剪强度参数

由表1发现，相对于单、三轴压缩试验，三轴卸荷试验下软岩抗剪强度参数均有显著降低，将单、三轴压缩状态近似作为洞室围岩内软岩初始(开挖前)赋存状态，则可通过上述软岩抗剪强度参数的劣化程度，修正洞室围岩开挖后卸荷区的抗剪强度参数值.

2.2 变形参数劣化分析

考虑到围岩所在区域的埋深和地应力条件[13]，重点探讨围压水平约为35MPa下的软岩变形参数的劣化特征.岩石的变形参数包括变形模量E和泊松比μ，由于围岩开挖卸荷过程对泊松比影响的变化不显著，故只分析对变形模量E的劣化效应.

根据单、三轴压缩试验，得到岩样不同围压水平下的变形模量，将其进行多项式拟合获得变形模量与围压的拟合关系：y=-0.0055x2+0.6603x+1.4068，进而得出35MPa围压下岩样单、三轴压缩的变形模量.

为了表征不同程度的卸荷效应，在进行卸荷阶段的分析之前，先引入卸荷率ω的概念，卸荷率ω表示卸荷围压变化量比上初始围压再乘以100%得到的数值，公式可表示为：

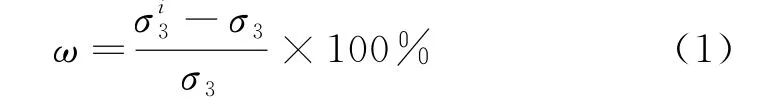
式中：σ3为初始围压值；σi3为卸围压过程中i时刻的围压值.

根据三轴卸荷试验，得到不同围压水平不同卸荷率(0%、20%、40%、60%、80%、100%)下 的 变 形 模量，类似于岩样三轴压缩变形模量的推求，可得出35 MPa围压水平不同卸荷率下岩样三轴卸荷变形模量.见表2.同时，表2还给出了三轴卸荷试验相对于三轴压缩试验变形模量的降幅.

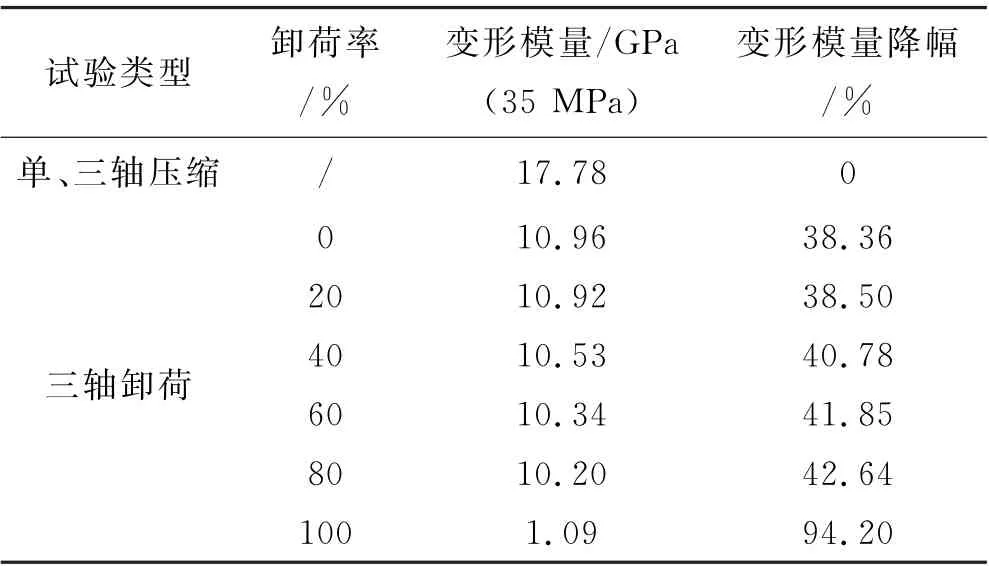
表2 单、三轴压缩试验和三轴卸荷试验变形模量

由表2 可知，相对于单三轴压缩试验的变形模量，三轴卸荷条件下各变形模量有不同程度的降低，将单、三轴压缩状态近似作为洞室围岩内软岩初始(开挖前)赋存状态，则可通过上述软岩变形参数的劣化程度，修正洞室围岩开挖后卸荷区的变形参数值.

3 深埋洞室软岩开挖卸荷参数修正

考虑到丹巴水电站引水隧洞地勘报告中有关卸荷区的初始力学参数取值仅通过经验和综合类比得出，结合文献[14-15]的研究，尝试以上述室内软岩卸荷力学参数劣化分析结果为依据，将单、三轴压缩状态近似作为洞室围岩内软岩初始(开挖前)赋存状态，对丹巴水电站引水隧洞开挖后卸荷区的初始力学参数进行修正.

3.1 强度参数修正

根据丹巴水电站地质勘察报告及已有研究资料[16]，丹巴水电站引水隧洞的初始力学参数见表3.由于围岩卸荷分区中，强卸荷区受扰动最为显著，为了便于研究，针对初始力学参数，主要对洞室围岩开挖强卸荷区的粘聚力c和内摩擦角φ进行修正，弱卸荷区、断层及其余新鲜岩体(卸荷未扰动区)力学参数仍采用表3中初始力学参数进行计算.

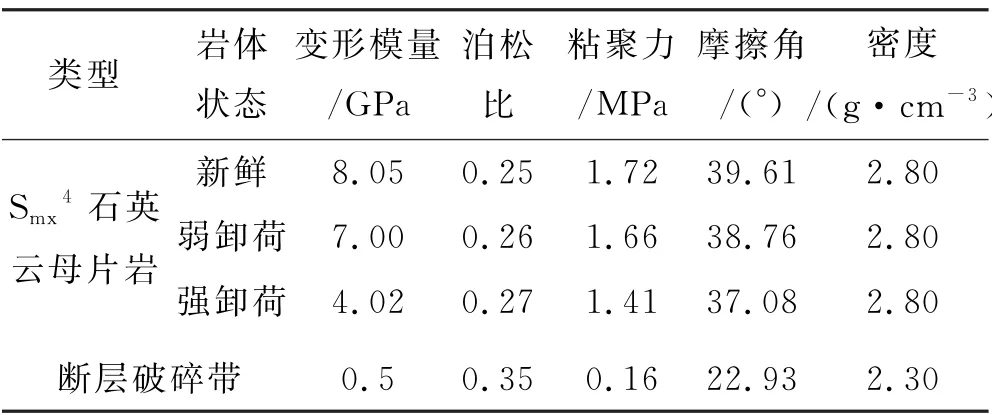
表3 洞室软岩开挖卸荷初始力学参数取值表

结合表1抗剪强度参数的降幅，以新鲜围岩参数为基准值，则软岩洞室开挖强卸荷区修正后的岩体粘聚力和内摩擦角分别为1.51MPa和33.26°，与初始参数整体比较接近，处于合理范围之内.

3.2 变形参数修正

如前所述，围岩开挖卸荷过程对泊松比影响的变化不显著，只考虑对变形模量E进行修正.

在此，首先引入应力释放率[17]的概念：在洞室开挖的瞬间还未产生位移时，开挖轮廓线上任一点M处于失衡状态，不平衡力记为P0，随后洞室在失衡力作用下向洞内发生收敛变形，无支护条件下，位移发生到一定程度时的不平衡力记做Pi，则定义此时M点应力释放率δ为：

结合前面卸荷率的概念，通过不同的应力释放率来模拟不同的卸荷率进而反映不同程度的卸荷效应.不同应力释放率下的参数可以通过不同卸荷率的试验结果进行修正，针对不同应力释放率，本文仅通过不同的变形参数进行表征.此外在FLAC3D中对不同应力释放率模拟时，除了上述提到的变形参数的修正外，反向施加的空间荷载也会发生变化.结合常见洞室围岩开挖卸荷应力释放率研究[18]，分别考虑了20%、40%、60%、80%应力释放率水平.由表2，以新鲜岩体的变形模量为基准值，对不同应力释放率下强卸荷区的变形模量做相应的修正，见表4.

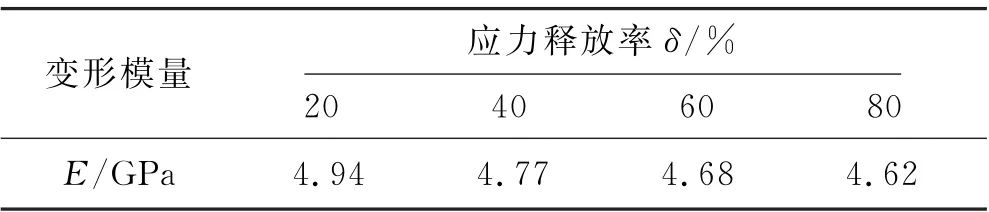
表4 不同应力释放率δ下的变形模量取值表

综上，将开挖卸荷后的参数汇总，见表5.

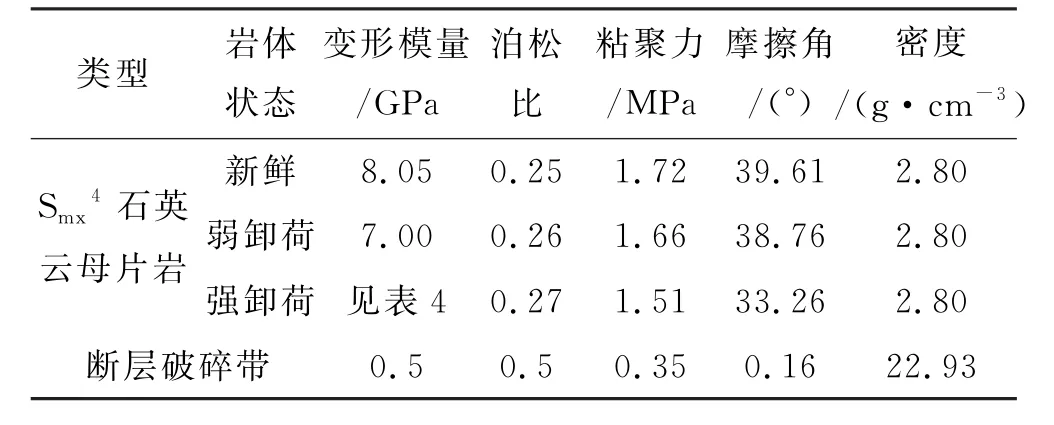
表5 洞室软岩开挖卸荷参数取值表

4 深埋洞室软岩围岩二次支护时机

基于上述参数修正的成果，以丹巴水电站左岸洞室埋深为1000m 且通过断层破碎带的一段引水隧洞为研究对象(见图1)，通过FLAC3D开展深埋洞室软弱围岩开挖卸荷-流变下不同二次支护时机对洞室变形影响的研究.

4.1 本构模型及参数

所建立模型(如图2 所示)中，圆型洞室洞径为16m，图中从里向外依次为开挖洞室、1.2m 厚C30混凝土、0.3m 厚C25混凝土、强卸荷区、弱卸荷区、断层破碎带和新鲜岩体.根据丹巴水电站地质勘察报告中松弛圈测试相关资料，同时参考类似工程卸荷影响区的划分方法[14]，本模型中强卸荷区取3m，弱卸荷区取10m.

图2 围岩洞室模型图

本文采用的流变模型为FLAC3D中的Cvisc模型，其中EM和EK分别为弹性模量和黏弹性模量，ηM和ηK 分别为Maxwell黏性系数和Kelvin黏性系数.当施加的应力σ小于Mohr-Coulomb准则的长期屈服应力σs时，元件的应力为零，本构方程可表示为：

当施加的应力σ大于或者等于Mohr-Coulomb准则的屈服应力σs时，元件基于Mohr-Coulomb准则发生塑性流动，本构方程可表示为：

计算中，开挖卸荷力学参数见表4和表5，开挖卸荷-流变参数根据地勘报告及类似研究资料[19]获取，见表6.

表6 软岩洞室卸荷-流变试验参数取值表

4.2 支护方案

初期支护方案为锚杆加混凝土，施工中边开挖边支护.二次支护选择等级为C30的混凝土进行衬砌，根据要求在不同时机进行施加，沿洞周布置1.2m厚.支护布置如图3所示.支护结构使用各向同性的弹性模型，其中，混凝土材料采用实体单元模拟，锚杆采用结构单元中的CableSEL单元模拟.

根据研究的需要，在初期支护混凝土的外边缘和二次支护衬砌混凝土的外边缘分别布置关键结点，关键结点分别为对应外边缘圆周上的四分点处，初期支护的关键结点命名A1、B1、C1和D1，二次支护的关键结点命名为A2、B2、C2和D2.如图4所示.

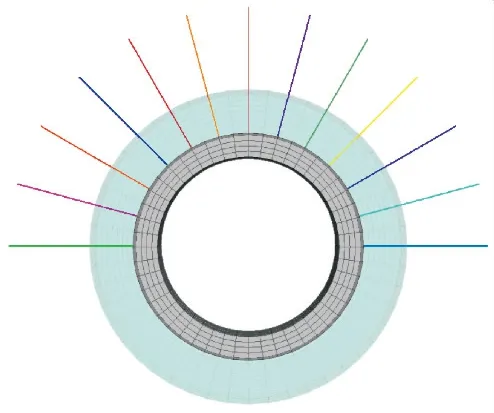
图3 支护布置

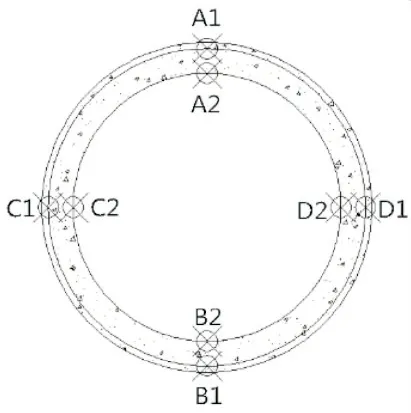
图4 关键节点布置

4.3 二次支护时机指标选取

考虑到围岩变形数据相对较易观察，考虑以拱顶和拱底的相对位(记为ΔA1B1)作为二次支护时机的参考标准.首先建立相对位移ΔA1B1与应力释放率δ的关系，建立方法如下：

1)初期支护后，未施加二衬的之前，应力释放率δ以0%开始取值，然后以5%等步长递增至100%(100%即表示不进行二次支护或不施加空间反向荷载)，监测不同应力释放率下30d时间内(设计上30d内施加二衬效果较好[20-22])关键节点A1、B1、C1 和D1产生的位移.

2)根据计算中关键点监测数据，建立应力释放率δ与相对位移ΔA1B1多项式拟合关系(如图5所示).相对位移ΔA1B1在应力释放率为100%时为301.14 mm，将此30d 相对位移定义为ΔA1B1max，然后取ΔA1B1max的20%(60.23mm)、40%(120.46mm)、60%(180.68mm)和80%(240.91mm)作为不同的二次支护时机.

图5 应力释放率与相对位移多项式拟合曲线

3)根据图5的关系曲线可得上述4种相对位移对应的应力释放率为25%、46%、67%和88%，通过表4可插值得出25%、46%、67%和88%应力释放率下的变形模量，其它参数同表5，通过FLAC3D模拟不同应力释放率，实现对洞室不同二次支护时机进行模拟.

4.4 长期运行中衬砌结构变形分析

在洞室的长期运行中，针对选定的4种二次支护时机，对二次支护后洞室的流变计算50a，分别统计出关键结点A2、B2、C2 和D2 在0～50a产生的变形，如图6所示.进一步分析发现：

1)尽管在30d内二次衬砌支护后变形量大小有差异，但是4种支护时机下5a左右洞室变形基本收敛，10a左右洞室变形完全收敛.

2)二次衬砌时机占ΔA1B1max的比例越大，二次衬砌后产生的收敛变形越小.由此可以看出，二衬支护前适度的让压可以使二衬后产生的变形减小.

3)二次衬砌后洞室流变变形经历了衰减流变阶段和稳定流变阶段.

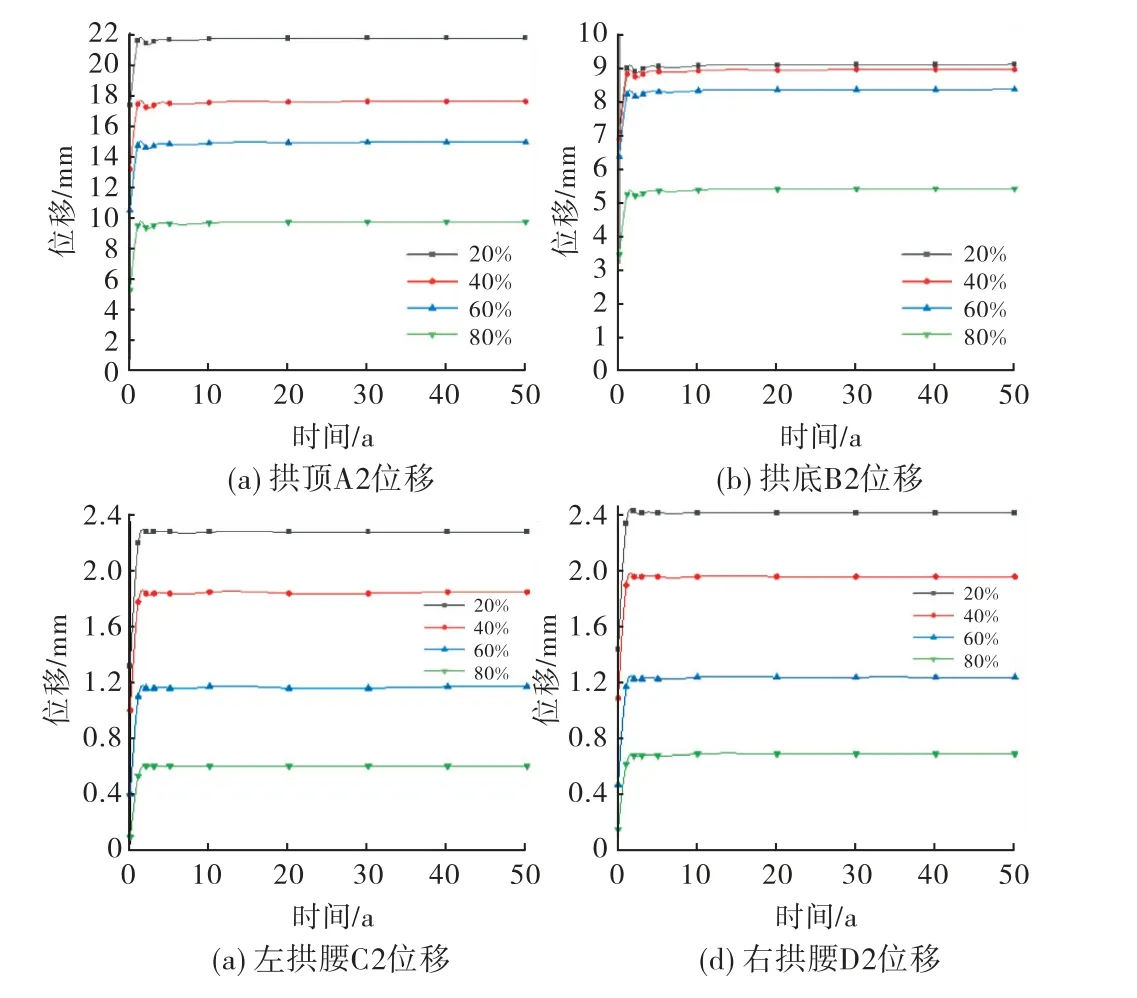
图6 不同二衬时机衬砌结构关键点位移

4.5 二次支护时机确定

以衬砌结构不同阶段的长期变形和应力值作为参考，进一步分析洞室围岩二次支护时机，分别列出运行时间为1年、5年、10年和50年的长期变形和第三主应力极值，见表7～8.

表7 不同二次支护时机下衬砌结构内长期变形统计表

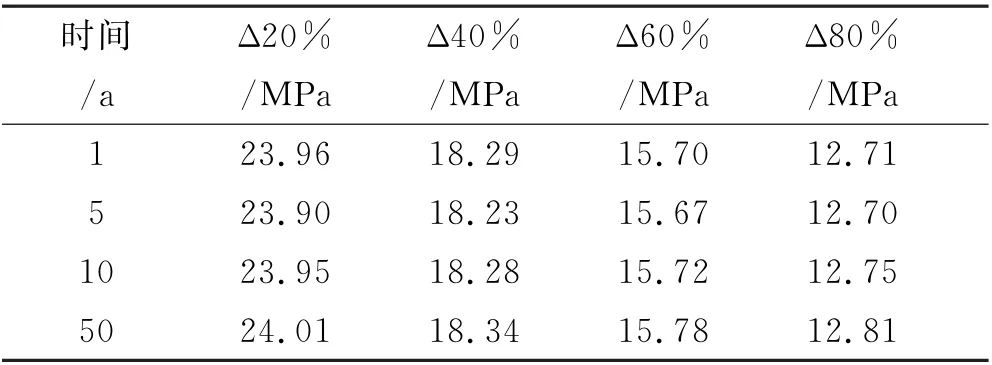
表8 不同二次支护时机下衬砌结构内长期应力极值统计表

由表7和表8可得：

1)在相同年限时，4种支护时机下，二次支护时机为ΔA1B1max的百分比越大，关键结点位移和衬砌结构内长期应力极值会越来越小，适度的让压对二衬长期位移和应力有促进作用.

2)相同二次支护时机下，随着时间的增长，衬砌结构内长期变形和衬砌结构内长期应力极值会随之增加.其中洞室变形在5年左右基本收敛，10年左右完全收敛.