人字闸门底枢摩擦副接触力学特性分析

赵新泽 周紫嫣 赵美云

(1. 三峡大学 水电机械设备设计与维护湖北省重点实验室， 湖北 宜昌 443002； 2.三峡大学 机械与动力学院， 湖北 宜昌 443002)

对人字闸门底枢的研究从20世纪90年代开始，主要集中在选材、构件加工工艺及润滑体系几个方面.由于人字闸门底枢摩擦副低速重载的特性，接触区容易出现润滑失效[1]，从而严重影响底枢寿命.因此对人字闸门底枢摩擦副的接触研究尤为重要，诸多学者采用软件仿真进行分析.岳陆游，丁建宁，杨继昌，等[2]用有限元软件对两接触零件的位移、应力和应变等参数进行计算，并对参数选择和结构设计进行了优化分析，结果表明，各参数优化计算中蘑菇头、帽皆处于弹性变形状态，且在有限元数值计算下外载作用面积、摩擦因数、球面半径和配合间隙等对接触变形的影响与赫兹公式理论分析结果一致；殷恋飞[3]应用有限元软件对参数选择和结构设计进行了优化设计，其结论说明，改变外载的作用面积以及接触表面粗糙度的变化对接触变形的参数影响不大，而减少底枢间隙可以有效地减少磨损，并且通过曲线拟合，对有限元分析结果进行了简单的二维拟合，可为人字闸门底枢蘑菇头的合理计算与设计提供一定的参考.

此外关于底枢摩擦副的数学模型，现有的文献中均采用赫兹接触模型对其进行分析[2-3]，求得底枢半径、载荷大小、底枢接触间隙与最大接触应力的关系，然而与底枢的工程实际却存在较大偏差.底枢设计中常采用两种经验公式[4]对底枢应力进行分析，但这两种经验公式只是给出底枢蘑菇头半径、外载荷对最大应力的影响，且仅仅反映蘑菇头的局部承压应力.

本文引入Fang接触模型分析人字闸门底枢摩擦副的接触力学特性.将人字闸门实际运行中对人字闸门摩擦副的接触力学特性产生影响的参数，如载荷、底枢半径、底枢接触间隙及底枢材料进行研究，为底枢设计提供理论依据.

1 人字闸门底枢摩擦副的接触模型

人字闸门底枢摩擦副由承轴巢中镶嵌的衬套(轴瓦)、半球形轴头(蘑菇头)、底座、垫板构成.由于在其运行过程中主要承受闸门自身重力、风压力、水压力等作用力，对人字闸门整体做受力分析，根据力和力矩的平衡条件可获得人字闸门底枢受到一个有倾角的合力作用.

本文研究底枢摩擦副的接触力学特性，对闸门做出以下假设：1)材料均匀，各向同性；2)接触表面光滑，忽略润滑介质；3)弹性变形仅发生在接触区域，符合胡克定律，且不超过材料的弹性极限；4)与两个接触体相比，接触区域的尺寸很小；5)闸门运行过程平稳且匀速，且合力不变.此时人字闸门底枢摩擦副的接触模型示意图如图1所示.

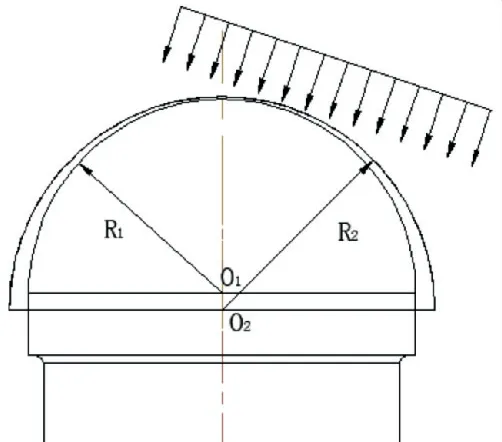
图1 闸门底枢接触模型草图

Fang接触模型建立在多位专家[5-9]的研究基础之上，用以分析弹性球面的共形压力分布的半数值、半解析模型.假设人字闸门底枢摩擦副的接触面积(即蘑菇头与轴瓦的接触面积)小于其整体尺寸，公式可表示如下[9]：

式中：P0是最大接触应力；a是接触区域边界轮廓的半径；r是表面上的点与对称轴之间的投影水平距离；n是 接 触 应 力 分 布 指 数；F2是 外 部 负 载；k1，k2分是与蘑菇头、轴瓦的杨氏模量和泊松比相关的参数；B是由n和Γ函数确定的函数；δ是两个物体在集中力方向上相互趋近的距离；Γ 是伽马函数；R1，R2是蘑菇头半径和轴瓦半径；ΔR=R2-R1；g、C是系数函数.

2 计算结果与分析

以某工程两个闸门为例，相关参数见表1.蘑菇头材料40Cr 的泊松比为0.277，杨氏模量为211 GPa；轴瓦材料选用QAL9-4的泊松比和杨氏模量分别为0.330、116GPa.Fang接触模型计算流程中，计算迭代误差参数给定0.1.

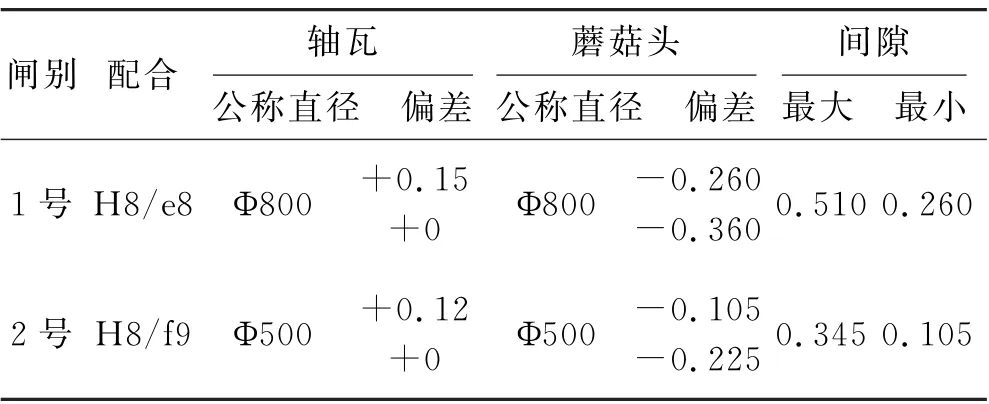
表1 闸门相关参数 (单位：mm)

2.1 赫兹接触与Fang接触

图2(a)和(b)为赫兹接触模型与Fang接触模型在不同间隙下的接触区域边界轮廓的半径变化曲线和最大接触应力变化曲线.其中aH、P0H为赫兹接触模型计算结果，aF、P0F为Fang接触模型计算结果.图2(c)与(d)将Fang接触模型的计算结果纵坐标的坐标尺放大.

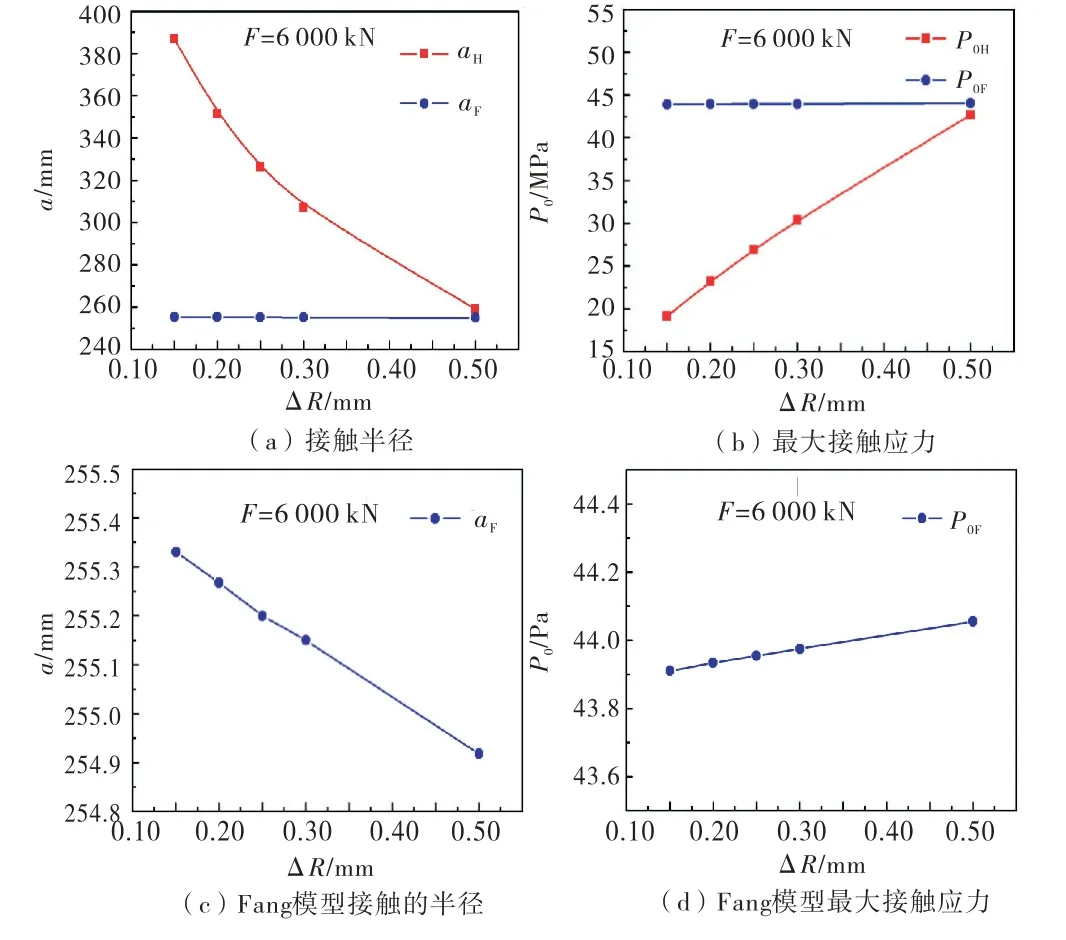
图2 Fang模型和赫兹模型下接触半径(或最大接触应力)随接触间隙的变化曲线

由图(a)和(b)可知，随着底枢轴瓦与蘑菇头间隙ΔR的增加，赫兹接触模型中接触区域边界轮廓的半径a有一个明显降低的趋势，故此时最大接触应力有明显增加.当ΔR由0.15mm 增加至0.5mm 时，aH由386.86mm 降为259.05mm，降低了33.04%，最大接触应力P0H由19.14MPa增至42.69MPa，增加了123.04%.与之相比Fang接触模型的下降趋势则不明显.如图2(c)所示，在Fang接触模型下，接触区域边界轮廓的半径a与间隙ΔR成负相关的关系；图2(d)所示，最大接触应力也有一定的增长，由43.91 MPa增至44.055MPa.

规定最大接触应力的相对误差为εP、接触区域边界轮廓的半径的相对误差为εa.其表达式如下：

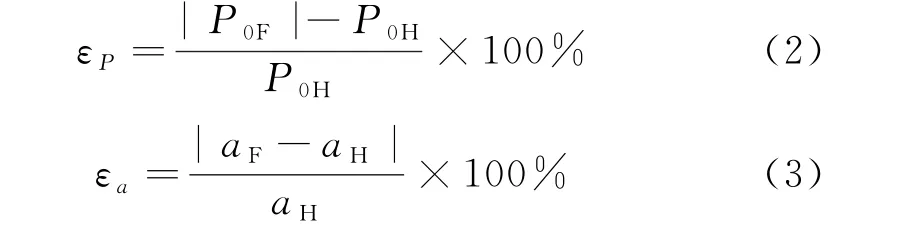
Fang接触模型与赫兹接触模型之间的相对误差如图3所示.当ΔR=0.5mm 且外载荷超过5500kN时，最大接触应力相对误差与接触区域边界轮廓的半径的相对误差均小于更小的接触间隙下的计算值，F=6000kN 时，接触区域边界轮廓半径的相对误差仅有1.62%，最大接触应力相对误差为3.10%.当ΔR=0.15mm 且F=7000kN 时，接触区域边界 轮廓半径的相对误差为67.85%，最大接触应力相对误差达到64.49%.根据赫兹接触模型，当接触间隙仅有0.1mm 的情况下，接触区域边界轮廓半径的计算结果为442.8mm，超过此时底枢半径.显然这表明赫兹接触模型不适用于小间隙或相对接触区域较大的接触.

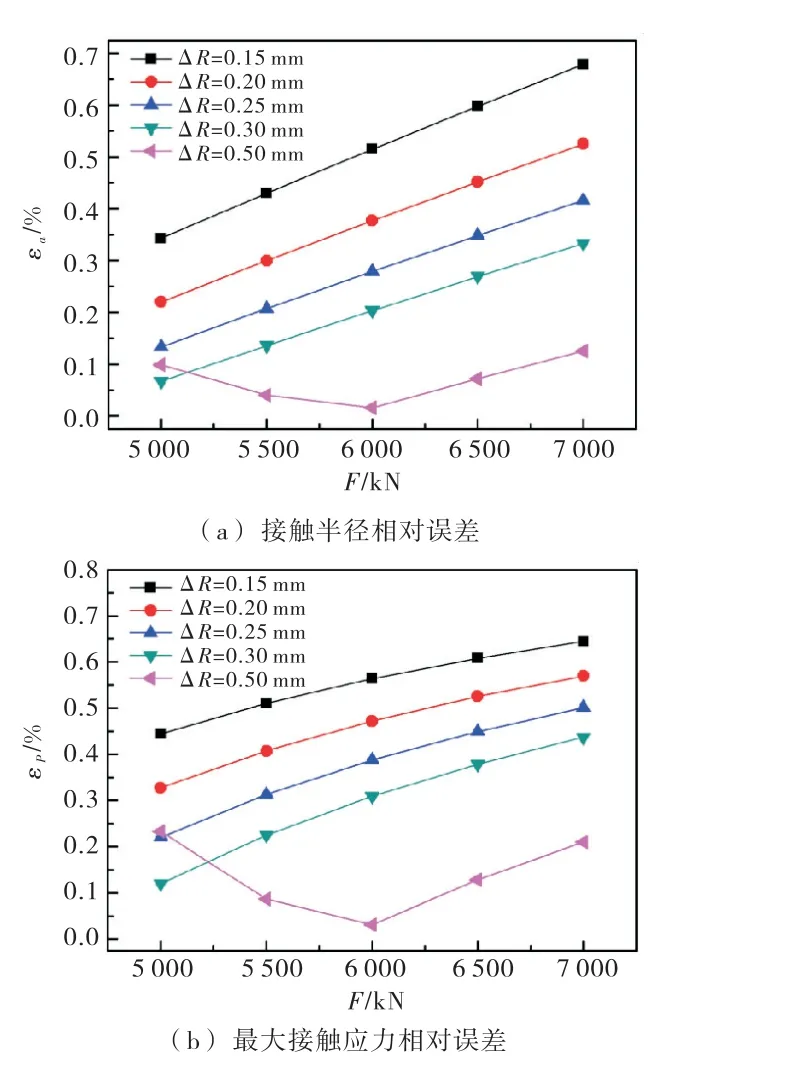
图3 赫兹接触模型与Fang接触模型之间的相对误差

2.2 有限元分析

利用Fang模型和有限元模型，能够分析球面滑动轴承的接触压力分布，并验证Fang理论模型运用在底枢摩擦副上的的有效性.使用Workbench确定的压力等高线如图4所示.

图4 底枢蘑菇头在不同载荷下接触压力分布曲线

有限元建模时的蘑菇头半径为250mm，蘑菇头与底枢的接触半径为0.3mm.此时利用Fang接触模型计算的最大接触应力与有限元计算的最大接触应力的相对误差在5000～7000kN 载荷下分别为7.74%、12%、4.65%、5%、0.7%.误差表明，Fang模型适用于确定球面底枢摩擦副的接触参数.故下文将采用Fang模型对底枢摩擦副进行分析计算.

2.3 外载荷对接触特性参数的影响

图5为底枢在5000～7000kN 载荷下的接触半径与最大接触应力变化曲线.

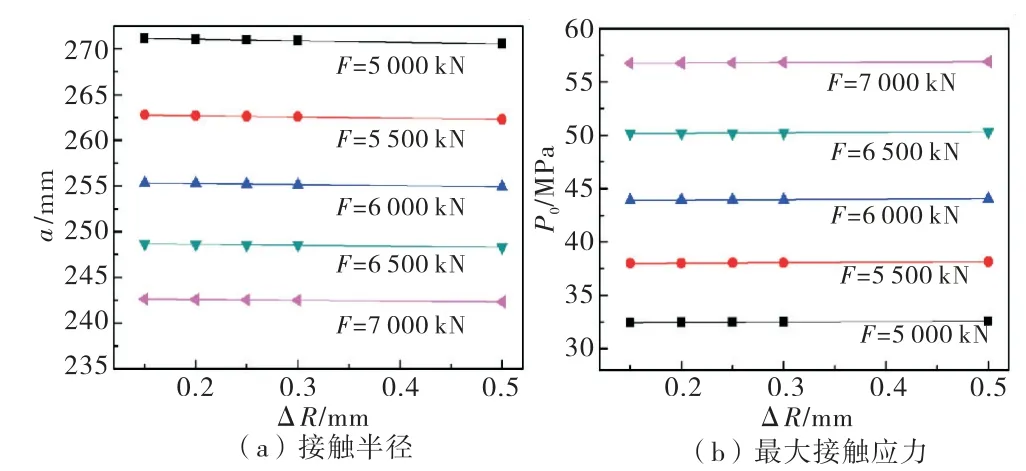
图5 外载荷与接触轮廓边界半径、接触应力的变化曲线

当载荷由5000kN 增长至7000kN，增加了40%，轮廓半径将减少12.5%.随着外载荷的增加，接触区域边界轮廓的半径有明显减小.载荷增加40%时，最大接触应力将同时增加95.8%.随着外载荷增加，最大接触应力相应地增加.显然，接触应力对外载荷更为敏感.

图6为不同外载荷下压力分布曲线，底枢蘑菇头表面应力关于外载荷对称.此时接触间隙ΔR=0.25 mm，随着载荷的增大，接触半径减小，而相应的接触压力增大.当载荷减小，接触应力分布曲线逐渐平坦，即随着载荷的减小，接触应力分布趋势变化越小.可知在重载时，应力更集中，会加剧底枢摩擦副的磨损以至失效.故在设计底枢摩擦副时，必须要将载荷值作为最关键的参数纳入设计方案.

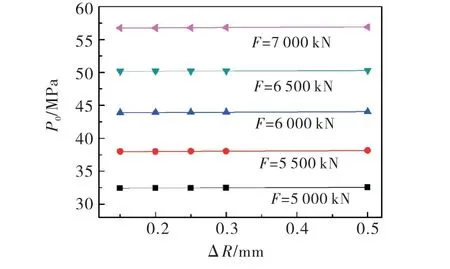
图6 不同外载荷下底枢蘑菇头压力分布曲线

2.4 底枢半径对接触特性参数的影响

图7为接触间隙固定0.3mm 时，不同尺寸底枢在变化载荷下对底枢接触特性参数的影响.

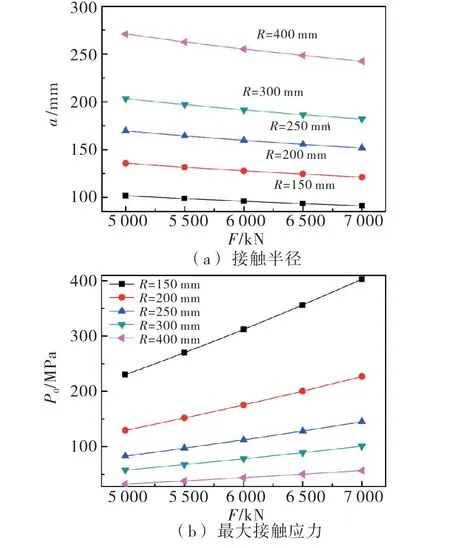
图7 底枢半径与接触轮廓边界半径、接触应力的变化曲线

当外载荷为6000kN 时，底枢半径由150mm 增至200mm，半径增大33.3%，其接触区域边界轮廓的半径增大33.2%；底枢半径由300mm 增至400 mm，半径增大33.3%，其接触区域边界轮廓的半径增大33.2%，表明在相同载荷下接触区域边界轮廓的半径与底枢半径成正比关系，随着底枢半径的增加，接触区域边界轮廓的半径增加.不同底枢半径值的“F-a”曲线图为近乎相互平行的直线段，如图7(a)所示，可知接触区域边界轮廓的半径与底枢半径存在的正比关系几乎不受载荷影响.

如图7(b)所示，当外载荷为5000kN 时，底枢半径由150mm 增至200mm，半径增大33.3%，最大接触应力减小43.66%；底枢半径由300mm 增至400 mm，半径增大33.3%，最大接触应力减小43.66%，表明在相同载荷下最大接触应力与底枢半径存在一个反比的关系，随着底枢半径的增加，最大接触应力明显减小.此时，不同底枢半径值的“F-P0”曲线图为呈现“楔形”，表明载荷对这种反比关系有一定的影响.当外载荷为7000kN 时，底枢半径增大33.3%，最大接触应力降低43.69%.故在极端苛刻重载的情况下，底枢半径对最大接触应力的影响增加，在适用范围内增加底枢半径尺寸，则可以更有效地降低最大接触应力.

图8为不同底枢半径下压力分布曲线，此时外载荷为6500kN，随着底枢半径的增大，接触区域边界轮廓的半径增大，接触应力峰值减小，故相应的接触应力减小.分布曲线随着底枢半径的增大而平缓，故增大底枢半径可有效地减少应力集中，降低接触区域的摩擦与磨损，提高底枢工作可靠性.

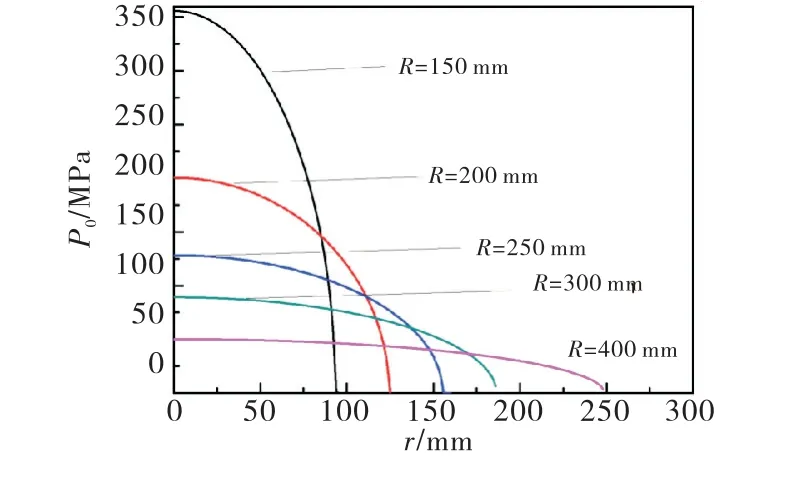
图8 不同半径下底枢蘑菇头压力分布曲线

2.5 接触间隙对接触特性参数的影响

图9为5组接触间隙与接触区域边界轮廓的半径、最大接触应力的变化曲线.在5000kN 外载荷作用下，间隙为0.15mm 时，接触区域边界轮廓的半径为271.13mm，最大接触应力为32.43MPa；间隙为0.5mm 时，接触区域边界轮廓的半径为270.55mm，最大接触应力为32.575MPa；此时接触区域边界轮廓的半径减小0.58 mm，最大接触应力增加0.447%.即随着间隙增大，接触区域边界轮廓的半径有微弱的下降趋势，最大接触应力增大.整体而言，接触间隙对接触参数的影响较小，因此底枢制造加工中，严格保证配合公差就足以将间隙对接触带来的影响减弱.

图9 接触半径与接触轮廓边界半径、接触应力的变化曲线

2.6 材料的杨氏模量与泊松比对接触特性参数影响

对于底枢蘑菇头和轴瓦的材料，通常有以下材料，见表2.

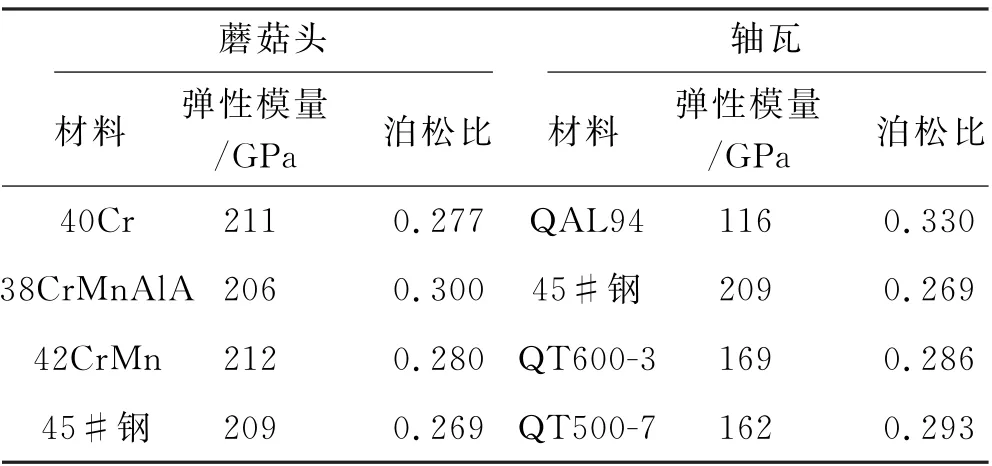
表2 底枢摩擦副的材料

在底枢半径固定为400mm，接触间隙为0.25 mm 时，选定配对副材料.蘑菇头材料为40Cr，轴瓦材料为QAL94，此时接触区域边界轮廓的半径为a1，最大接触应力为P01.规定：Δax=ax-a1，ΔP0x=P0x-P01.其中脚标x代表配对副序号，见表3.

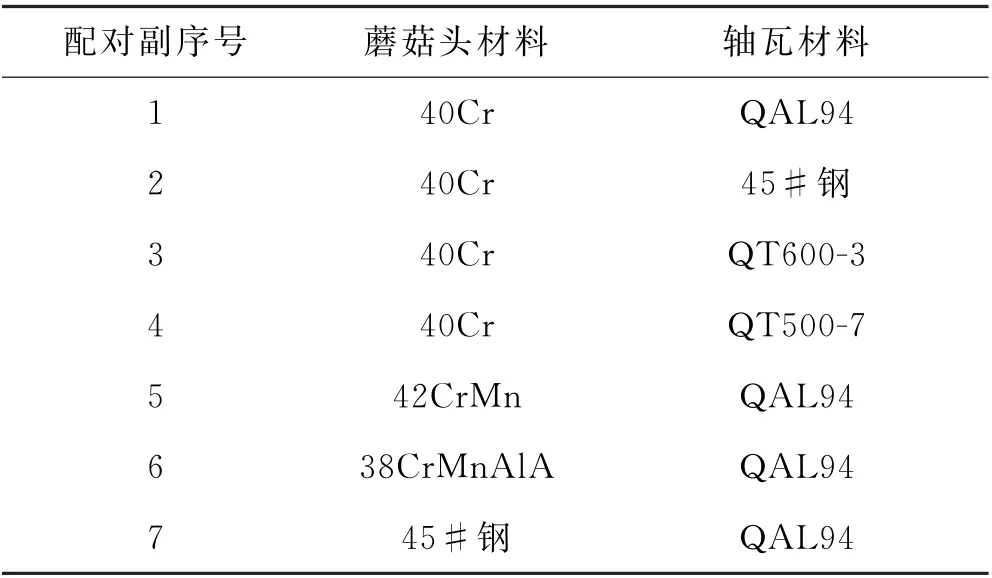
表3 配对副序号

图10为2～7号配对副与1号配对副的接触区域边界轮廓的半径差值及最大接触应力差值.不同材料的配对副的a、P0存在一定区别.其中6号与7号配对副接触性能更优，有更大的接触区域和更低的接触应力.随着外载荷的增加，2、3、4、6、7号配对副的接触区域面积与1号配对副相比区别变小，而接触应力的区别变大.因此，在重载的情况下，2、3、4号配对副会加剧底枢的磨损，而6、7号配对副对底枢的接触性能有所改良.

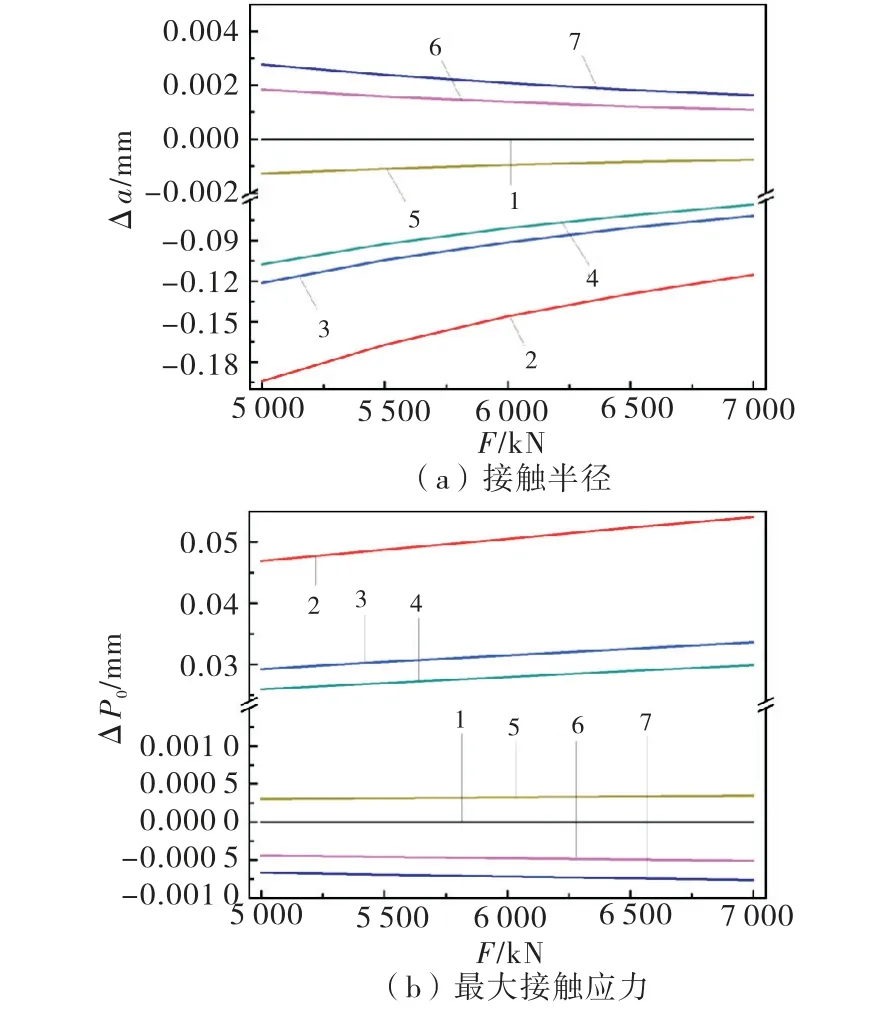
图10 摩擦副材料与接触轮廓边界半径差、接触应力差的变化曲线

分析得知材料的杨氏模量对底枢的接触性能有影响.杨氏模量值越大，接触区域面积越小，即表面形变越小，这对底枢的润滑起正面作用；但同时杨氏模量值越大，最大接触应力将越大.因此，可以选择通过表面加工工艺处理，如渗碳、氮化、硬质阳极氧化、镀铬、表面淬火等使表面硬度增强，同时可选择相对柔性的金属材料作为配对副材料.

3 结 论

1)Fang接触模型表明，外载荷与底枢半径对人字闸门底枢摩擦副的接触性能有重要影响.接触面积随着外载荷增加而减小，最大接触应力随着外载荷增加而增大；底枢半径增大，接触面积成比例增大、最大接触应力成比例减小，且在极端苛刻重载的情况下，底枢半径对最大接触应力的影响增大.

2)接触间隙与底枢配对副材料对人字闸门底枢摩擦副的接触性能也有一定影响.在不考虑润滑的情况下，严格保证配合公差将控制间隙对底枢摩擦副接触性能的影响.从减少摩擦和磨损的角度出发，选择渗碳、氮化、硬质阳极氧化、镀铬、表面淬火等处理方式的柔性材料将提高耐磨性，同时有效降低最大接触应力.