大规模压气储能洞室稳定性和洞周应变分析

夏才初，张平阳，周舒威，周 瑜，王 蕊

（1.同济大学 地下建筑与工程系，上海 200092；2.中国大唐集团新能源股份有限公司，北京 100053）

1 引 言

压气储能（compressed air energy storage，简称CAES）是一种利用压缩空气作为介质来储存能量和发电的技术。在用电低谷时，用电网中多余的电能驱动空气压缩机，把空气压缩进地下洞室储存起来，到用电高峰时，再把高压空气放出，并与少量的气体燃料混合在气轮机燃烧室中燃烧而迅速膨胀做功，进而带动发电机发电[1]。作为压缩空气储能电站主要组成部分的地下储气构造物是压气储能电站选址的决定因素，也是保障其运行性能和可靠性的技术关键，一般是利用已开采完的贮气和贮油的地质构造、地下含水层、已开采或专门开凿的盐岩溶腔、硬岩中人工开挖的地下洞室等[2]。前3种都是利用特殊的地质构造，在风能富集或用电需求量大而需建压气储能电站的地区不一定存在这类地质构造。因此，在岩石中人工开挖地下洞室便成为这些地区压气储能电站最可能选择的地下构造物方案。

迄今，世界上仅建成了两座商业化运行的压气储能电站，第一座是1978年建成的德国Huntorf电站[3]（290 MW），另一座是1991年建成的美国阿拉巴马州的McIntosh电站[4]（110 MW），其地下构造物都是利用盐岩溶腔。美国于1981年启动了Soyland压气储能项目，利用硬岩洞室作为储气构造物，最终以失败告终[5]。美国 Norton Energy Storage LLC公司正在设计利用石灰岩洞的压气储能项目[2,6]。日本利用硬岩洞室进行了压气储能的小型试验[7]，韩国正在进行利用硬岩洞室的压气储能的试验[8]。目前还没有商业化运营的利用硬岩洞室的压气储能电站。Lu[9]对瑞典的岩石内衬洞室（lined rock cavern，简称LRC）的径向位移和围岩塑性区进行了计算。Zimmels等[10]使用FLAC计算了圆形洞室在不同水平构造应力、不同内压和不同洞室间距时围岩的塑性区，得出了合理的洞室布置间距。但是，对于洞室方案选型，只考虑洞室稳定性是不够的，还要兼顾洞室的密封性能，故应从塑性区和洞周应变两个方面进行分析。塑性区能较好地反映围岩受力的危险区域，洞周应变量则是密封材料选择的基础数据。

我国拟计划修建一个装机容量为 105kW 的压气储能电厂，所需地下洞室容积为 105m3，洞内最大气压为10 MPa，洞址区岩性为花岗岩，围岩级别为Ⅱ级，初始地应力为自重应力场，不考虑地下水的影响。拟在衬砌内表面施作高分子材料密封层对洞室进行密封。为建设一个安全稳定运营的地下洞室，需对高内压下洞室围岩稳定性和洞周应变进行研究。在典型的洞室埋深（200、300、500 m）下，取隧道式（包括圆形和马蹄形两种截面）和大罐式两种洞室形式，并考虑不同的洞室尺寸，应用Abaqus有限元软件计算出高内压作用下的围岩塑性区和洞周应变。通过分析比较，获得适合该工程的洞室形式，并为密封材料在不同温度下的延伸率和耐久性研究提供了基础数据。

2 压气储能洞室及其有限元模型

2.1 压气储能洞室方案

隧道式压气储能洞室由一条或多条并行隧道组成，暂不考虑隧道间的相互影响。选择圆形和马蹄形两种截面，两者的截面积相等，圆形截面选择洞径为15、10、6 m，马蹄形截面选择宽度为18、12、7 m，洞室埋深取200、300、500 m。混凝土衬砌厚度取50 cm。

大罐式压气储能洞室形似内衬岩洞储气库[11－12]，拱顶和底部呈半球形，中间圆柱体连接拱顶和底部，形状类似煤气罐。大罐式压气储能洞室选择两种尺寸：①拱顶和底部呈25 m半径的半球形，中间圆柱体高为25 m，开挖体体积为1.16 × 105m3（有效容积约为 105m3）；②拱顶和底部呈半径为20 m的半球形，中间圆柱体高为 20 m，单洞开挖体体积5.9 × 1 04m3（有效容积约为5 × 104m3），需建两个洞室，暂不考虑洞室间的相互影响。混凝土衬砌厚度取50 cm。

2.2 屈服准则和参数选取

围岩材料假定为理想弹塑性材料，采用摩尔-库仑屈服准则：

式中：σ1为最大主应力（MPa）；σ3为最小主应力（MPa）；c为岩石的黏聚力（MPa）；ϕ为岩石的内摩擦角（°）。

围岩级别为Ⅱ级，其弹性系数和强度参数取值参照《公路隧道设计规范》(JTG D70－2004)中的范围，并根据经验取值，详见表1。

表1 围岩物理力学参数Table1 Physico-mechanical parameters of surrounding rock

混凝土材料假定为弹性材料，其强度参数按照设计取值参照《水工隧洞设计规范》(DL/T5195-2004)，详见表2。

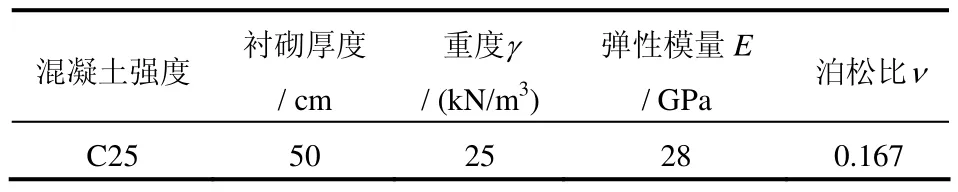
表2 混凝土衬砌物理力学参数Table 2 Physico-mechanical parameters of concrete

2.3 模型尺寸和边界条件

隧道式洞室左右及下边界取3倍洞径，洞室上方取实际埋深以计算地表变形。隧道断面在二维平面模拟中假定为平面应变问题。计算模型的左右边界分别受到x轴方向的位移约束；模型的地层下部边界受到y轴方向的位移约束；地表则为自由边界，未受任何约束。采用四边形网格进行划分，200 m埋深下洞室网格见图1(a)、1(b)。

大罐式洞室左右及下边界取3倍洞径，洞室上方取实际埋深以计算地表变形。该洞室用轴对称模型进行模拟。计算模型的左右边界受到x轴方向的位移约束；模型的地层下部边界受到y轴方向的位移约束；地表则为自由边界，未受任何约束。采用四边形单元进行划分，200 m埋深下洞室网格见图1(c)。

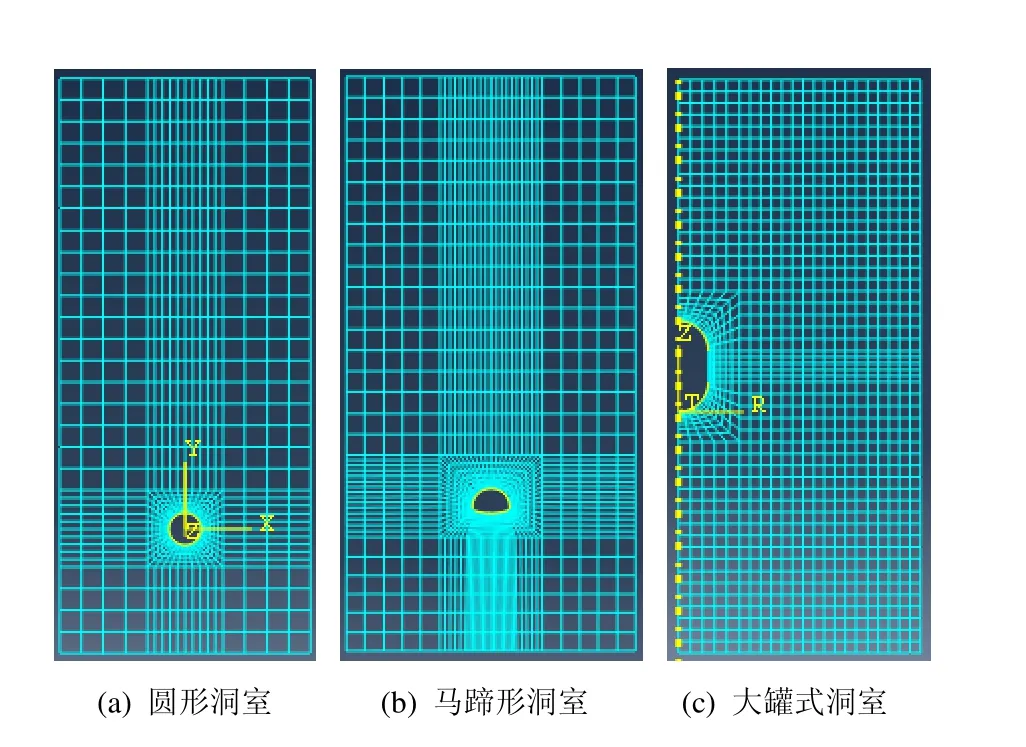
图1 压气储能洞室有限元网格示意图Fig.1 Sketch of FEM meshes of CAES cavern

计算工况分为3步：第1步，初始地应力平衡；第2步，洞室开挖，应力重分布；第3步，浇筑衬砌，施加10 MPa内压，获得充气后围岩塑性区和衬砌应变。

3 计算结果及讨论

3.1 圆形洞室

3.1.1 开挖后洞室稳定性

在同一埋深下，不同直径的圆形洞室开挖后塑性发展程度基本一致，塑性区面积与洞室截面积之比基本相同，直径为15 m圆形洞室开挖后塑性区见图2。以直径为15 m洞室为例，当埋深为200 m时，洞室围岩在开挖后大多处于弹性状态，只在洞壁表层出现部分塑性区，开挖引起的地表沉降为0.97 mm。当埋深增加至300 m时，洞壁塑性区深入围岩约1 m，开挖引起的地表沉降为1.56 mm。当埋深为500 m时，洞室洞壁上出现较大塑性区，深入围岩达1.8 m，开挖引起的地表沉降为2.93 mm。

3.1.2 充气后洞室稳定性和变形

图2 不同埋深下直径15 m的圆形洞室开挖后的塑性区Fig.2 Plastic zone of 15 m-diameter round cavern in various buried depths after excavation

不同埋深下，10 MPa内压下圆形洞室的剪切破坏塑性区见图3～5。从图中可以看出，在同一深度范围内，改变洞径对充气形成的塑性区范围影响不大。以15 m直径洞室为例，当埋深为 200 m和300 m，围岩自重小于内压，由充气引起的洞室塑性区主要集中在拱顶和底部，此时的地表隆起量分别为0.75 mm和0.14 mm；当埋深为500 m，围岩自重略大于内压，洞顶和洞底塑性区明显减小，此时地表沉降量为1.24 mm。

图3 埋深200 m不同洞径的圆形洞室充气后的塑性区Fig.3 Plastic zones of round cavern in the buried depth of 200 m after inflation

图4 埋深300 m不同洞径的圆形洞室充气后的塑性区Fig.4 Plastic zones of round cavern in the buried depth of 300 m after inflation

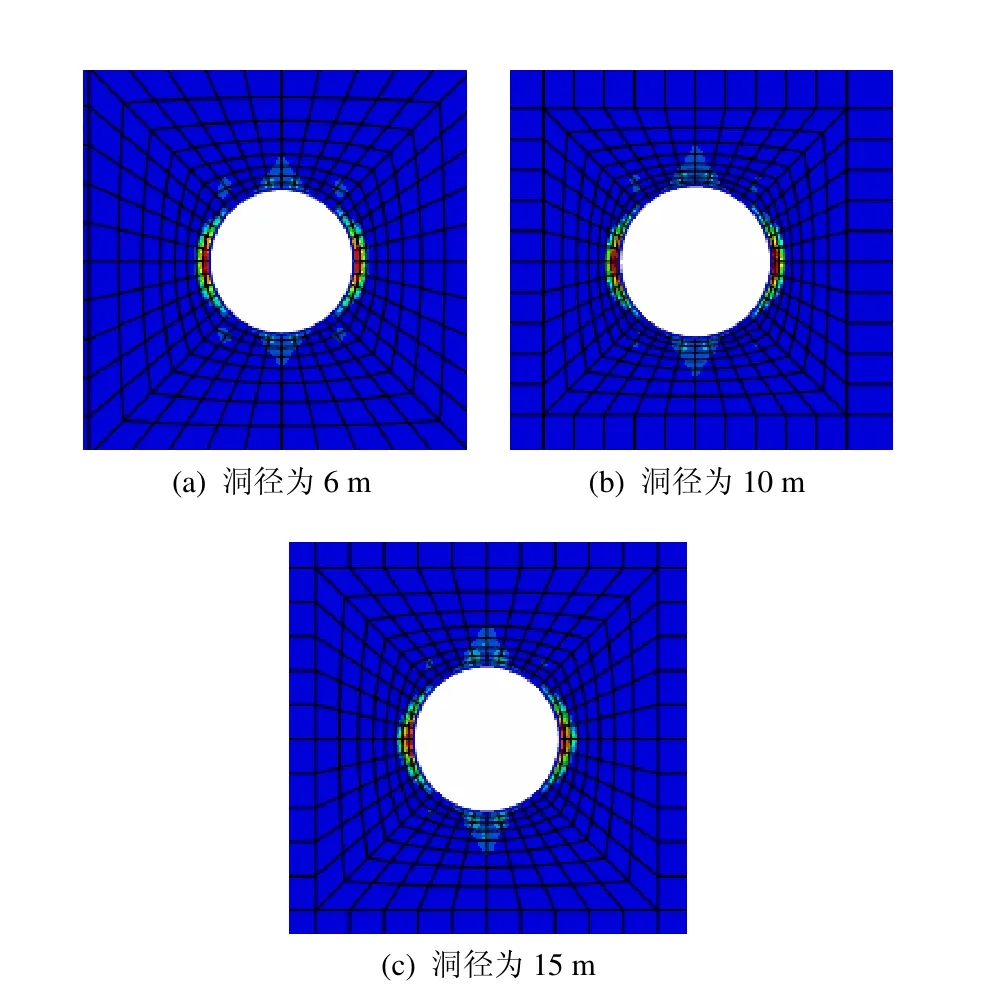
图5 埋深500 m不同洞径的圆形洞室充气后的塑性区Fig.5 Plastic zones of round cavern in the buried depth of 500 m after inflation

充气后洞室围岩可能处于受拉状态，圆形洞室围岩第一主应力最大值见表 3，可见，围岩未出现张拉破坏。

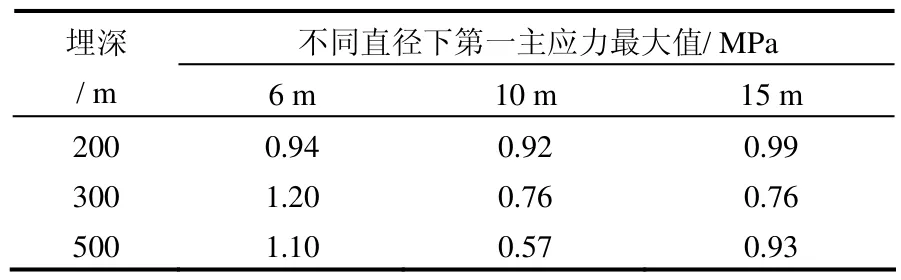
表3 圆形洞室围岩第一主应力最大值Table 3 Maximum of major principal stress of round cavern

洞室最大洞周应变分布位置与塑性区对应，最大洞周应变位于拱顶，洞室底部洞周应变与拱顶接近，最小洞周应变位于侧壁。200 m埋深下，对于直径为6 m的洞室，拱顶和侧壁上的洞周拉应变值分别为7.77 × 10−4和4.75 × 1 0−4；对于直径为10 m的洞室，拱顶和侧壁上的洞周拉应变值分别为9.58 × 10−4和5.26 × 1 0−4；对于直径为15 m的洞室，拱顶和侧壁上的洞周拉应变值分别为11.48 × 10−4和5.49 × 10−4。在同一洞室中，最大洞周应变比最小洞周应变大约1倍。

洞径的变化对洞周应变的影响明显。不同埋深下，不同洞径圆形洞室最大洞周应变见图 6。在200 m埋深下，10 m直径洞室最大洞周应变比6 m直径洞室大23.3%，15 m直径洞室最大洞周应变比10 m直径洞室大19.8%。相对而言，埋深的变化对洞周应变影响不大。对于15 m直径洞室，当埋深从200 m增至300 m时，最大洞周应变只减小了8.5%；当埋深从300 m增至500 m时，最大洞周应变只减小了4.8%。

圆形洞室充气后混凝土衬砌的内力值见表 4。剪力和弯矩对衬砌的影响较小，轴力对衬砌的影响为主要因素。埋深越大、洞室直径越小，相应的轴力越小。

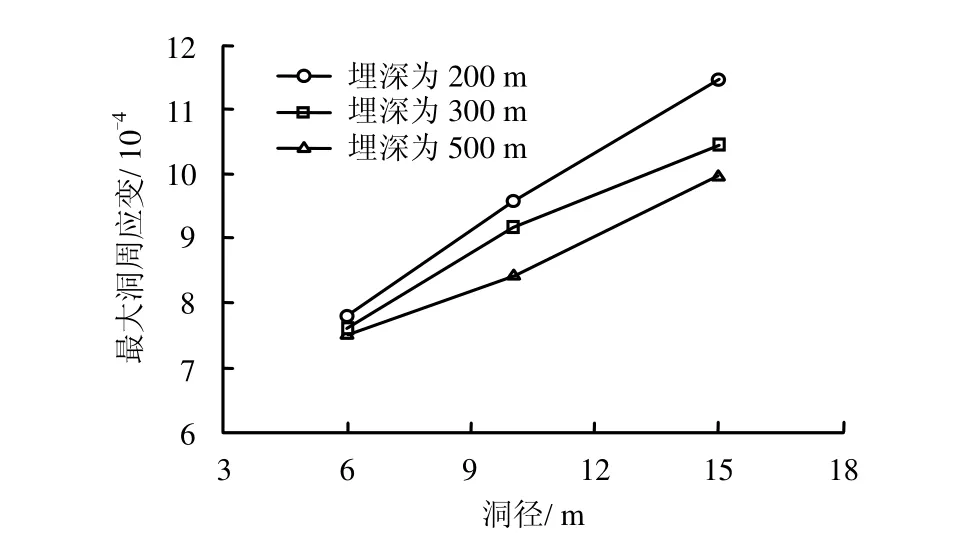
图6 圆形洞室最大洞周应变与洞径的关系Fig.6 Relationships between maximum tangential strain and diameter of round cavern

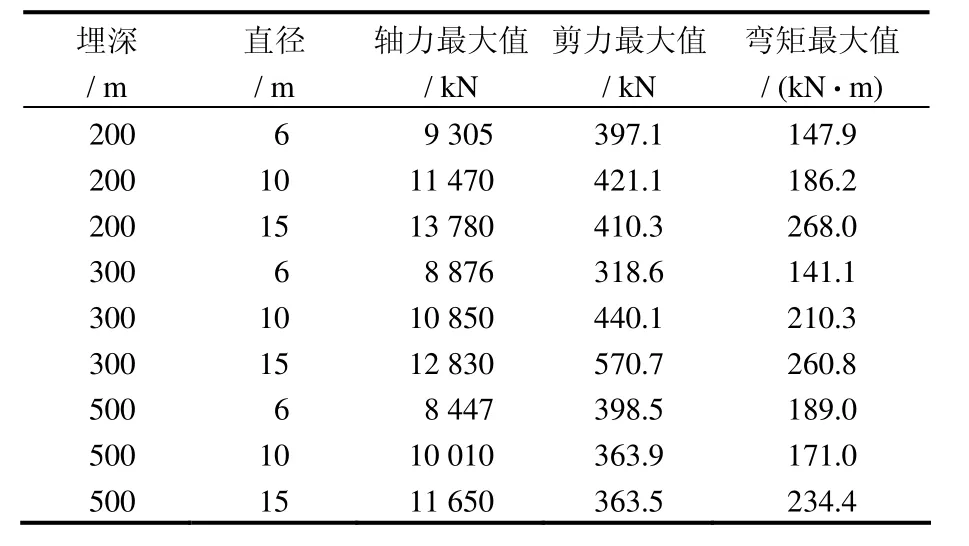
表4 圆形洞室混凝土衬砌内力值Table 4 Internal force values of concrete lining of round cavern

混凝土衬砌材料参考了高压隧洞的计算方法，假定为弹性材料。在计算所得的轴力作用下，衬砌已经开裂，故衬砌轴力较正常值偏大，有待进一步研究。

3.2 马蹄形洞室

3.2.1 开挖后洞室稳定性

不同跨度的马蹄形洞室开挖后塑性区基本相同，跨度18 m的马蹄形洞室开挖后塑性区见图7。从图中可以看出：当埋深为200 m时，塑性区主要集中在边墙上；当埋深为300 m和500 m时，在拱脚下出现了狭长的塑性区。18 m宽洞室在 200、300、500 m埋深下开挖后地表沉降量分别为1.07、1.77、3.46 mm。

3.2.2 充气后洞室稳定性和变形

不同埋深下马蹄形洞室充气后剪切破坏塑性区见图 8～10。在同一深度范围内，改变洞径对压气洞室形成的塑性区范围影响不大。当埋深为 200、300 m时，即埋深较浅时，由充气引起的洞室塑性区主要集中在拱顶和仰拱处，地表隆起量分别为0.83、0.11 mm；当埋深为500 m，即埋深较深时，充气后的塑性发展程度相比开挖引起的塑性小很多，地表沉降量为1.61 mm。

图7 不同埋深下跨度18 m的洞室开挖后的塑性区Fig.7 Plastic zones of 18 m wide cavern in various buried depths after excavation

图8 埋深200 m不同跨度的马蹄形洞室充气后的塑性区Fig.8 Plastic zones of horseshoe cavern in buried depth of 200 m after inflation

图9 埋深300 m不同跨度的马蹄形洞室充气后的塑性区Fig.9 Plastic zones of horseshoe cavern in buried depth of 300 m after inflation

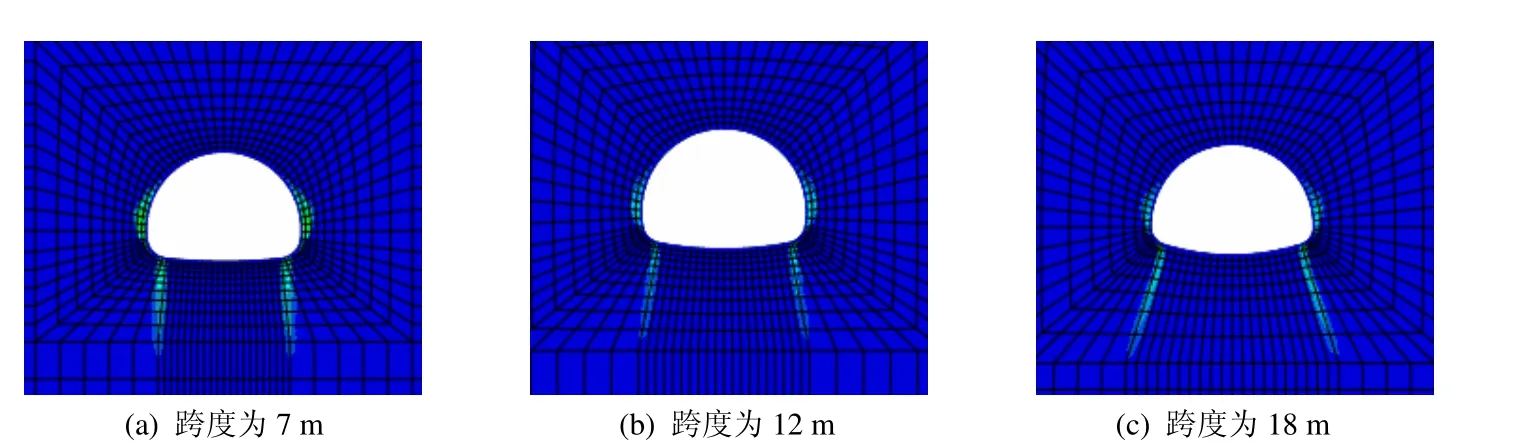
图10 埋深500 m不同跨度的马蹄形洞室充气后的塑性区Fig.10 Plastic zones of horseshoe cavern in buried depth of 500 m after inflation

充气后洞室围岩可能处于受拉状态，马蹄形洞室围岩第一主应力最大值见表5，可见，跨度为7 m和12 m洞室围岩出现张拉破坏。

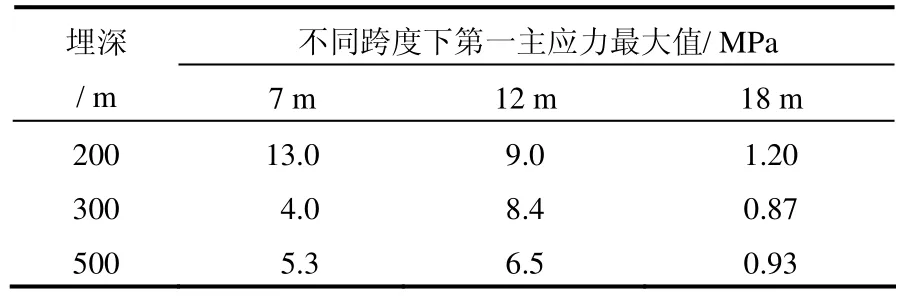
表5 马蹄形洞室围岩第一主应力最大值Table5 Maximum major principal stresses of horseshoe cavern

在同一洞室中，不同位置的洞周应变相差较大，最大值位于拱脚，最小值位于仰拱中点。200 m埋深下，对于跨度7 m洞室，拱顶、拱脚、仰拱三处洞周应变分别为4.07 × 10−4、10.72 × 10−4、4.4 × 10−5，对于跨度12 m洞室，拱顶、拱脚、仰拱三处洞周应变为 4.17 × 10−4、12.53 × 10−4、−0.66×1 0−4，对于跨度18 m洞室，拱顶、拱脚、仰拱三处洞周应变为3.73 × 10−4、13.24 × 10−4、−1.0 × 1 0−4。

不同埋深下，不同跨度洞室最大洞周应变见图11。埋深变化对洞周应变影响不大。当埋深增加时，各种跨度洞室洞周应变均减小，但变化不大，以跨度为18 m洞室为例，埋深从200 m增至300 m时，最大洞周应变减小1.7%，埋深从300 m增至500 m时，最大洞周应变减小2.9%。相对而言，跨度的变化对洞周应变的影响较明显。在200 m埋深下，跨度12 m洞室最大洞周应变比跨度7 m洞室大16.0%，跨度18 m洞室最大洞周应变比跨度12 m洞室大6.5%。

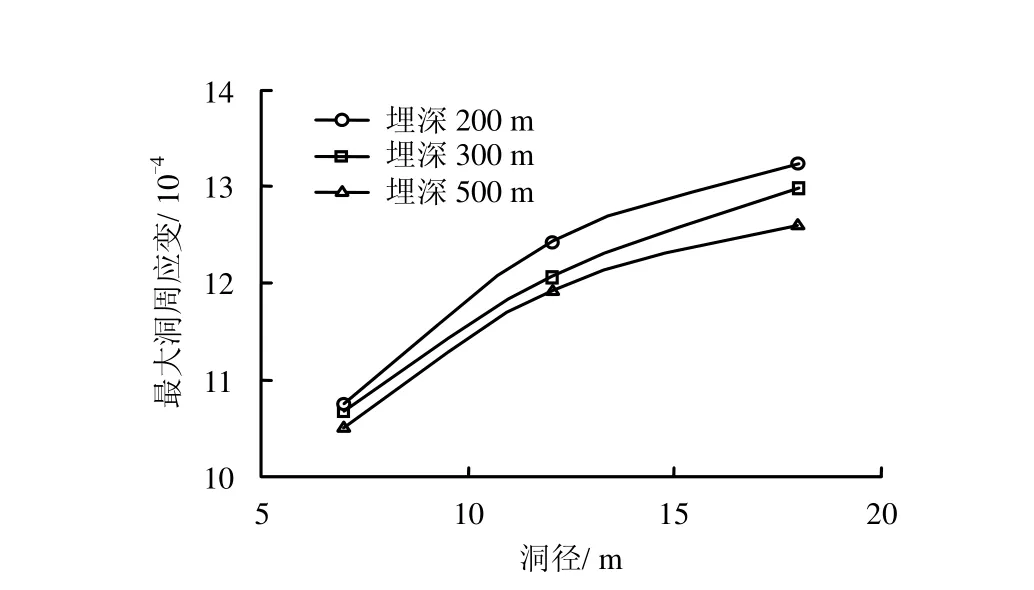
图11 马蹄形洞室最大洞周应变与洞径的关系Fig.11 Relationships between maxium tangential strain and diameter of horseshoe cavern

马蹄形洞室充气后混凝土衬砌的内力值见表 6。与圆形洞室相比，马蹄形洞室的剪力和弯矩值更大，而轴力值则与圆形洞室相近。故从衬砌受力的角度比较，圆形洞室更合理些。

表6 马蹄形洞室混凝土衬砌内力值Table 6 Internal force values of concrete lining of horseshoe caverns

3.3 大罐式洞室

3.3.1 开挖后洞室稳定性

两种尺寸的大罐式洞室开挖后塑性区基本相同，容积为 105m3大罐式洞室开挖后塑性区见图12。从图中可以看出，埋深为200 m和300 m的洞室围岩在开挖后基本处于弹性状态，出现小部分塑性区，基本位于洞壁表面，地表沉降量分别为0.29 mm和0.39 mm，洞室整体稳定性良好。埋深为500 m 的洞室侧壁出现较大塑性区，深入围岩9 m，地表沉降量为0.90 mm。

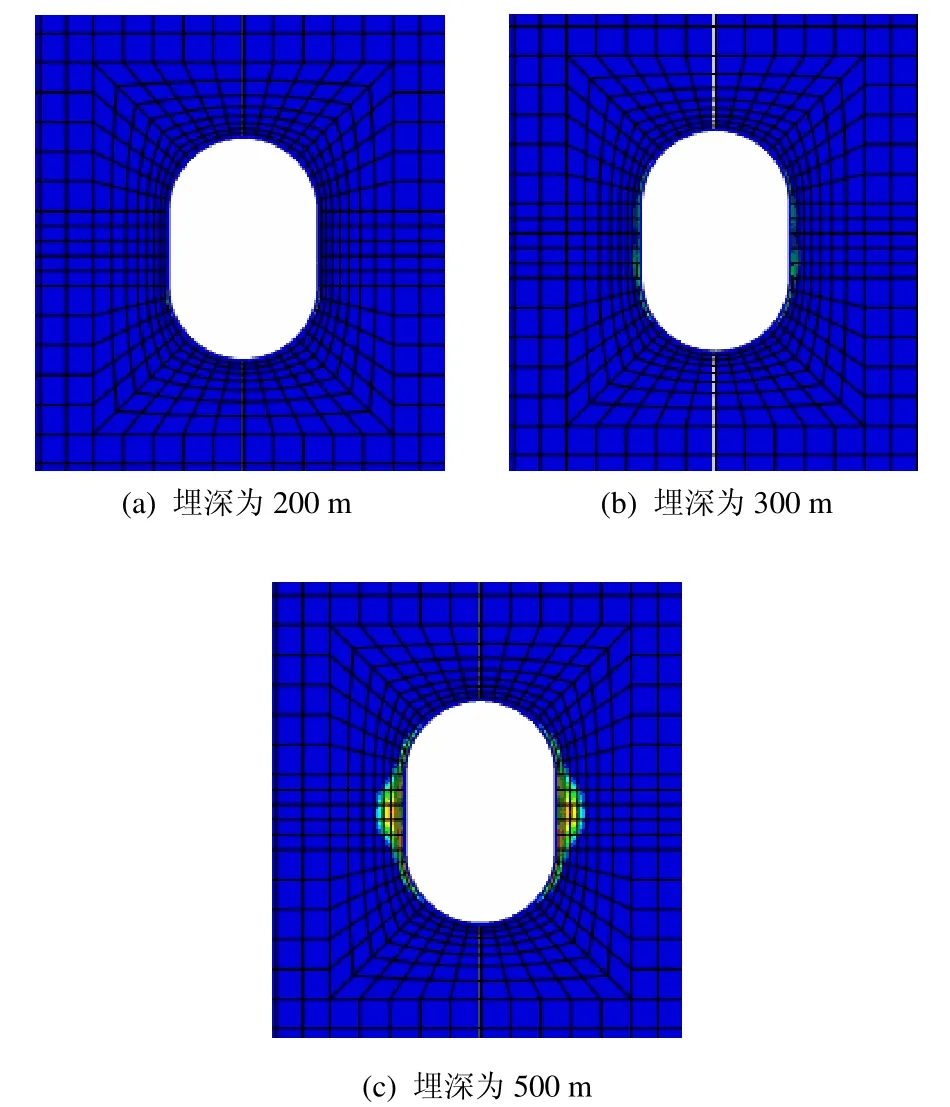
图12 不同埋深下105 m3大罐式洞室开挖后的塑性区Fig.12 Plastic zones of jar cavern with the volume of 100 thousand cubic meters in various buried depths after excavation

3.3.2 充气后洞室稳定性和变形

大罐式洞室的充气后剪切破坏塑性区见图13～15。将埋深为200 m的两种尺寸洞室进行比较发现，尺寸改变几乎不影响洞室塑性区范围，埋深300 m和500 m时情况亦如此。将容积为 105m3洞室置于200、300、500 m埋深下，拱顶塑性区逐渐减小，地表变形量分别为隆起0.32 mm、隆起0.27 mm、沉降0.23 mm。

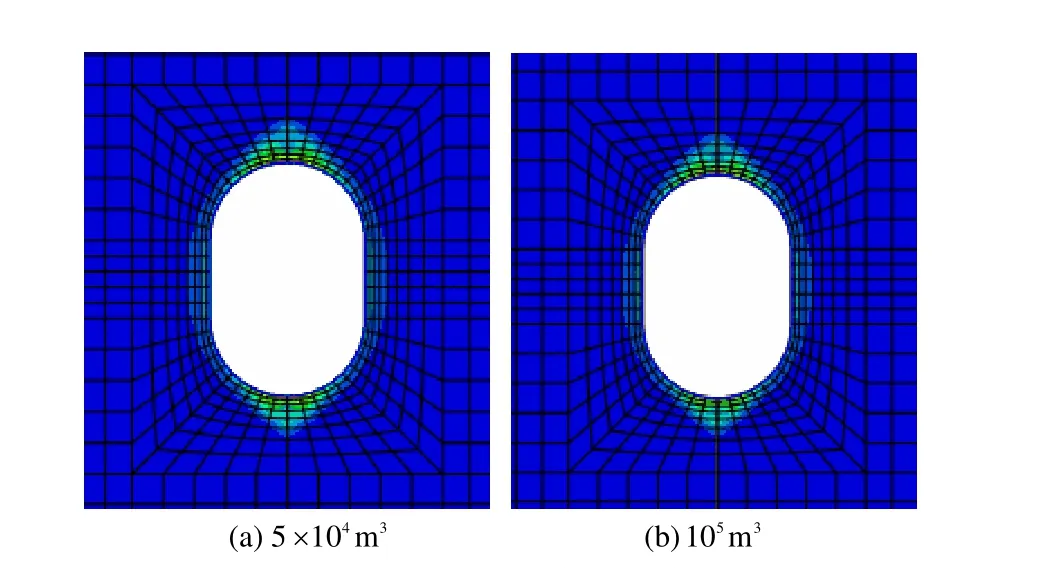
图13 埋深200 m不同容积大罐式洞室充气后的塑性区Fig.13 Plastic zones of jar cavern in buried depth of 200 m after inflation

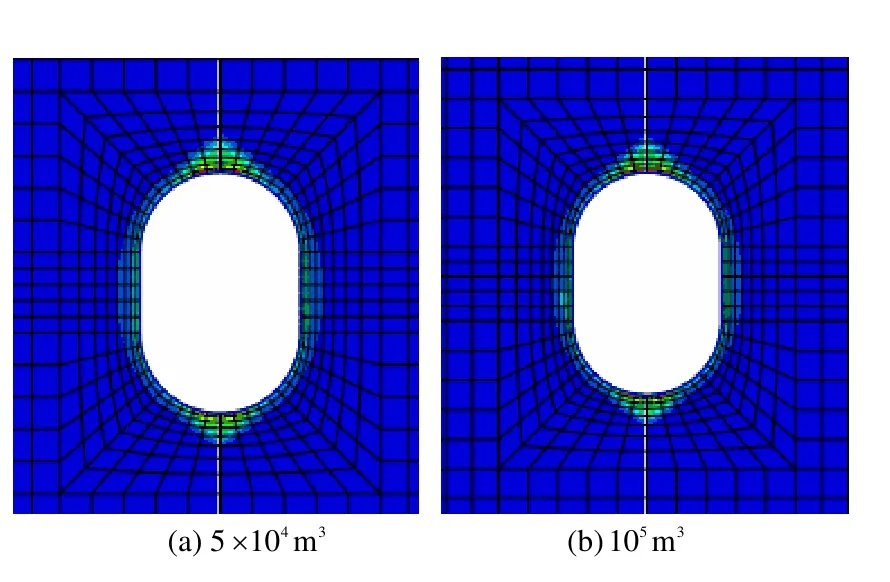
图14 埋深300 m不同容积大罐式洞室充气后的塑性区Fig.14 Plastic zones of jar cavern in buried depth of 300 m after inflation

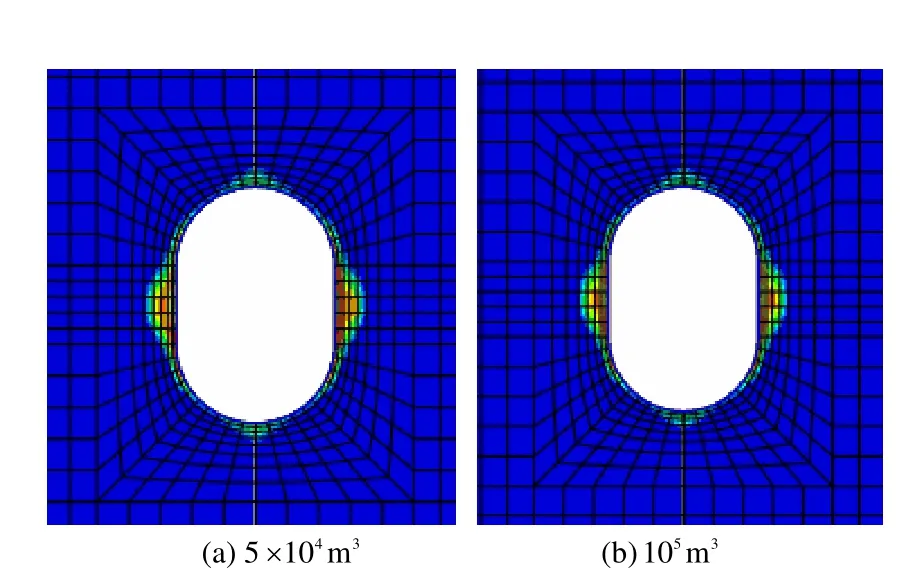
图15 埋深500 m不同容积大罐式洞室充气后的塑性区Fig.15 Plastic zones of jar cavern in buried depth of 500 m after inflation

充气后洞室围岩可能处于受拉状态，大罐式洞室围岩第一主应力最大值见表 7。由表可见，围岩未出现张拉破坏。

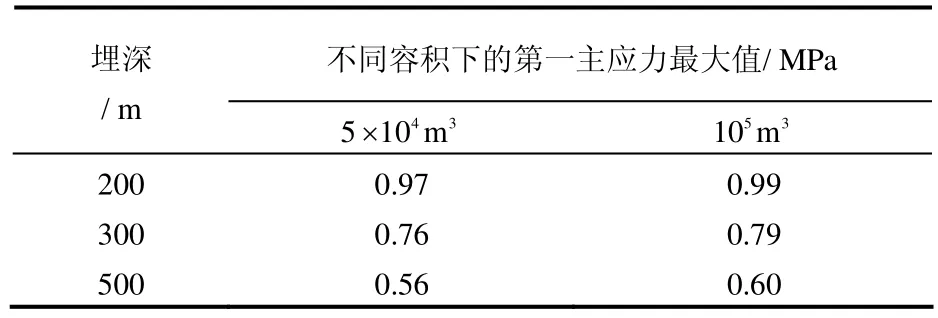
表7 大罐式洞室围岩第一主应力最大值Table7 Maximum major principal stresses of jar caverns

不同埋深下两种尺寸洞室最大洞周应变相差不大（见表8），可见，洞室尺寸的改变对洞周应变影响不大。相对而言，埋深的影响更大些。对于105m3洞室，300 m埋深下洞周最大主应变比200 m 埋深时分别减小了7.0%，500 m埋深下洞周最大洞周应变比300 m埋深时分别减小了10.5%。

表8 大罐式洞室最大洞周应变与洞室尺寸的关系Table 8 Relationships between maximum tangential strain and dimension of horseshoe cavern

大罐式洞室充气后混凝土衬砌的最大主应力值见表 9。与圆形和马蹄形洞室相比，大罐式洞室所受拉应力更小。

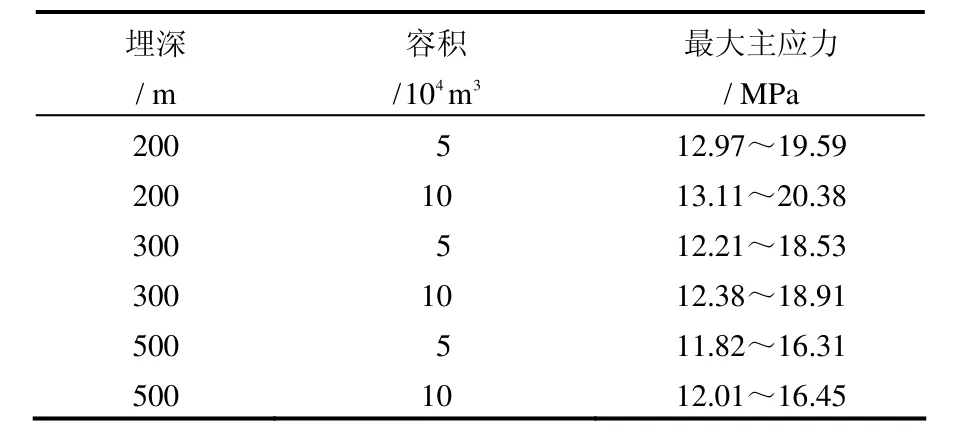
表9 大罐式洞室混凝土衬砌最大主应力Table9 Maximum principal stresses of concrete lining of jar caverns

4 结 论

（1）埋深为300 m的圆形洞室和大罐式洞室稳定性相对较好，适合作为压气储能地下构造物。各洞型洞室整体稳定性良好，在一定的支护措施下都具有可行性。在埋深和洞室尺寸两个影响洞室稳定性的因素中，埋深起主要作用。当埋深为200 m时，充气工况比开挖工况更危险；当埋深为500 m时，则是开挖工况较为危险；而当埋深取300 m 时，开挖和充气引起的塑性区发展程度相近，较200 m和500 m埋深时更安全。

（2）获得了在10 MPa内压下，Ⅱ级围岩中不同洞径和埋深的圆形、马蹄形和大罐式压气洞室的洞周应变，为密封材料的延伸率和耐久性研究提供了基础数据。其中，300 m埋深下6 m直径圆形洞室最大洞周应变为7.55 × 1 0−4，300 m埋深下7 m宽马蹄形洞室最大洞周应变为10.69 × 1 0−4，300 m埋深下容积为 5 × 104m3的大罐式洞室最大洞周应变为5.54 × 10−4，三者都在一般橡胶类高分子材料的正常工作范围内。

（3）洞型是影响洞周应变的主要影响因素之一。在计算的所有模型中，马蹄形洞室洞周应变最大（最大洞周应变范围为 1.053 × 1 0−3～13.24×10−4），圆形洞室次之（最大洞周应变范围为7.55×10−4～11.48× 10−4），大罐式洞室最小（最大洞周应变范围为4.99 × 10−4～6.07 × 1 0−4）。

（4）洞室尺寸是影响洞周应变的另一主要影响因素，尤其是对隧道式洞室。洞室尺寸越大，洞周应变越大。当埋深300 m时，直径10 m圆形洞室最大洞周应变比直径 6 m圆形洞室大 21.5%，宽12 m马蹄形洞室最大洞周应变比宽7 m马蹄形洞室大12.7%，105m3大罐式洞室最大洞周应变比5 × 104m3大罐式洞室大2.0%。

（5）埋深也是影响洞周应变的主要影响因素，对大罐式洞室影响尤为明显。一般而言，埋深越大，洞周应变越小。

[1]李仲奎,马芳平,刘辉.压气蓄能电站的地下工程问题及应用前景[J].岩石力学与工程学报,2003,22(增刊1):2121－2126.LI Zhong-kui,MA Fang-ping,LIU Hui.Underground engineering problems in compressed air energy storage and its developing future[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(Supp.1): 2121－2126.

[2]徐新桥,杨春和,李银平.国外压气蓄能发电技术及其在湖北应用的可行性研究[J].岩石力学与工程学报,2006,25(增刊 2): 3387－3392.XU Xin-qiao,YANG Chun-he,LI Yin-ping.Review on compressed air energy storage abroad and its feasibility application to Hubei Province[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(Supp.2):3387－3392.

[3]CROTOGINO F,MOHMEYER K U,SCHARF R.Huntorf CAES: More than 20 years of successful operation[J].Natural Gas,2001,45(50): 55.

[4]SCHALGE R,MEHTA B.The Alabama electric compressed air storage cavern from planning to completion[C]//Proceedings of the American Power Conference.Chicago I L: Illinois Inst.,1993: 998－1003.

[5]SALTER M G,MACFARLANE I M,WILLETT D C,et al.Design aspects for an underground compressed air energy storage system in hard rock[C]//ISRM Symposium on Design and Performance of Underground Excavations.London: British Geotechnical Society,1984: 37－44.

[6]SUCCAR S,WILLIAMS R H.Compressed air energy storage: Theory,resources,and applications for wind power[R].Princeton: Princeton Environmental Institute,Princeton University,2008.

[7]HAYASHI M.Rock mechanics of compressed air energy storage and super magnetic energy storage in Japan[J].Rock Mechanics in Japan,1991,(6): 50－57.

[8]KIM H M,LETTRY Y,PARK D,et al.Field evaluation of permeability of concrete linings and rock masses around underground lined rock caverns by a novel in-situ measurement system[J].Engineering Geology,2012,137－138: 97－106.

[9]LU Ming.Finite element analysis of a pilot gas storage in rock cavern under high pressure[J].Engineering Geology,1998,(49): 353－361.

[10]ZIMMELS Y,KIRZHNER F,KRASOVITSKI B.Design criteria for compressed air storage in hard rock[J].Energy and Environment,2002,13(6): 851－872.

[11]JOHANSSON J.High pressure storage of gas in lined rock caverns: Cavern wall design principles[D].Stockholm: Division of Soil &Rock Mechanics Royal Institute of Technology,2003.

[12]张筱萍,王金昌,杨森,等.内衬岩洞储气库(LRC)应用前景分析[J].青岛理工大学学报,2009,30(6): 107－111.ZHANG Xiao-ping,WANG Jin-chang,YANG Sen,et al.Appliance foreground of lined rock caverns(LRC)[J].Journal of Qingdao Technological University,2009,30(6): 107－111.