降雨条件下不同非饱和参数的数值模拟研究

秦世伟 陈 俊 武亚军 赵 玮

(上海大学 土木工程系， 上海 200444)

降雨是边坡失稳的重要诱因之一[1-3].降雨会导致边坡内部孔压升高[4-5]，边坡土体参数降低[6-7]，有效应力减小[8-9]，从而导致滑坡的产生.滑坡会致使灾区建筑物受损，居民生命财产安全受到威胁，因此，对于降雨边坡渗透稳定的研究对认识降雨边坡入渗机理，防止边坡灾变具有十分重要的作用.

国内外对于降雨边坡的渗透稳定性研究较多，试验方面：杨宗佶，蔡焕，雷小芹，等[10]对典型砾石土滑坡堆积体破坏过程在降雨条件下的破坏过程进行了室内试验；万琪，岳夏冰，闫强，等[11]利用大型土工离心机及自主研发降雨装置，开展12组不同开挖—支护时序边坡模型试验.数值模拟方面：张珂峰[12]利用Geo-slope软件对降雨条件下的边坡渗透稳定性规律进行了数值模拟研究.但是以上研究均未考虑到气候边界的影响.

本文利用Geo-slope软件中的Seep/W， Sigma/W， Vadose/W 与Slope/W 4个模块进行耦合，对广西某边坡体在降雨气候边界条件下的温湿耦合进行了数值模拟，同时利用灰关联度理论对不同非饱和参数下的边坡的渗透稳定性进行了敏感性分析.

1 考虑蒸发的降雨入渗理论

1.1 蒸发-蒸腾下的渗流场

水的质量方程可以写成以下形式：

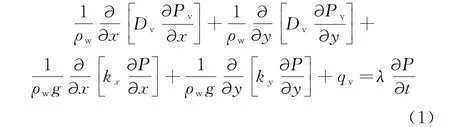
其 中：ρw是 密 度；Pv是 蒸 汽 压；Dv是 消 散 系 数；g是加速度；kx是x向渗透张量；ky是y向渗透张量；qv是 水 流 量；P是 总 压 力；λ是SWCC 曲 线 斜 率；t是 时间.

热传导方程则表示为：

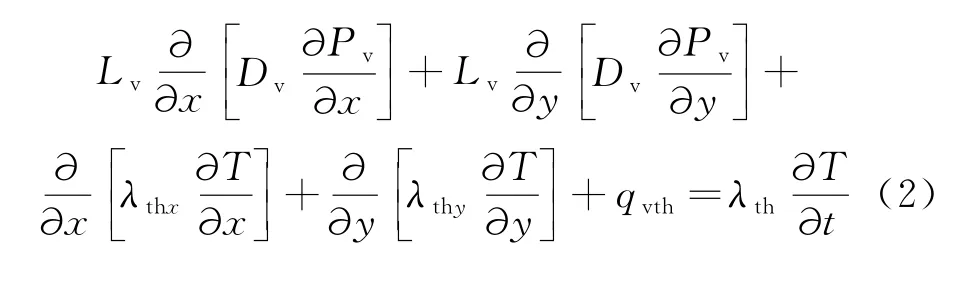
其中：Lv是热量系数；λthx是x向热导率；λthy是y向热导率；qvth是 热 量 函 数；T为 温 度 变 量；λth是 热 导率函数.

1.2 坡面的蒸发与蒸腾

降雨入渗与蒸发蒸腾作用互为反过程，蒸发量估算方程可以写成：

其中：E是坡面蒸发；Q是坡面辐射量；v是物化参数；A是湿度系数.

1.3 边坡安全系数理论

非饱和边坡抗滑稳定根据非饱和强度理论及Bishop极限平衡安全系数公式进行确定：

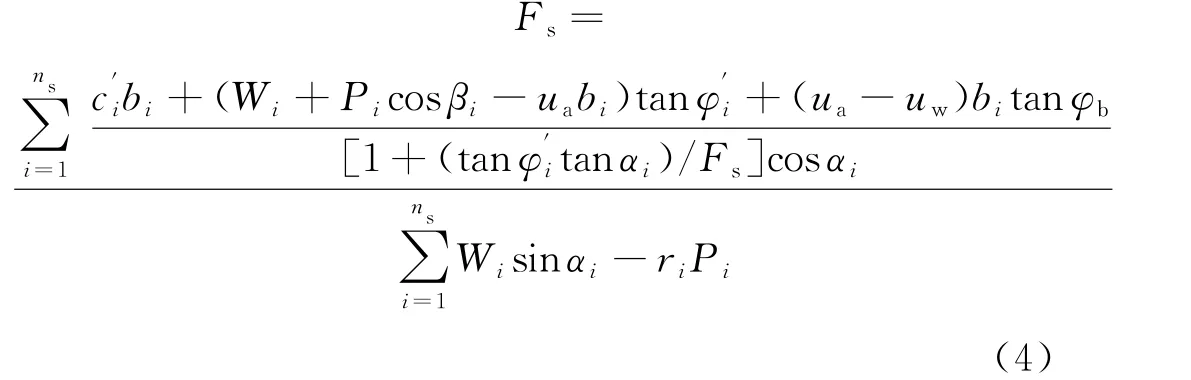
其 中：ci是 有 效 粘 聚 力；i是 编 号；Wi是 质 量；Pi是水压力；βi是倾角；ua是孔隙气压力；bi是土条宽度；φi是内摩擦角；uw是孔压；φb 是基质吸力贡献所的强度.

2 灰色关联度理论

2.1 比较矩阵、参考矩阵的选取

可以选取反映土体的非饱和程度的4个参数：a，m，n，k等 为 比 较 矩 阵，即：

将边坡的安全系数作为参考矩阵：

2.2 无量纲化矩阵形式

将比较矩阵与参考矩阵无量纲化，其中比较矩阵可以写成：

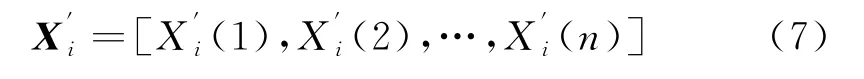
其中：

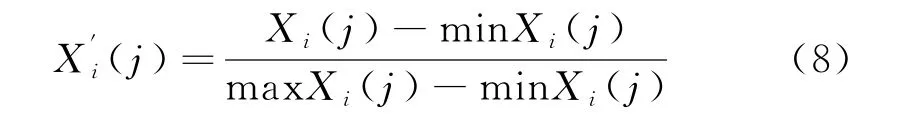
参考矩阵同理如下：

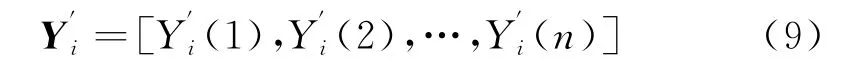
其中：

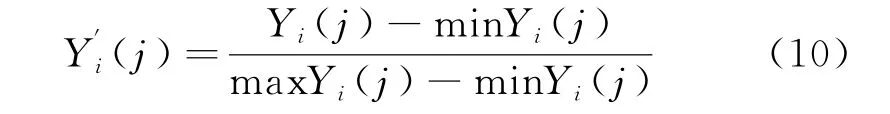
2.3 灰关联差异矩阵的计算

对无量纲化的参考矩阵与比较矩阵进行差异计算：

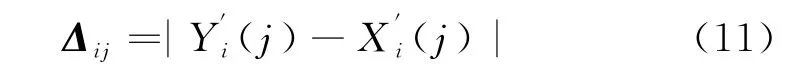
其中最大最小值可以写成：

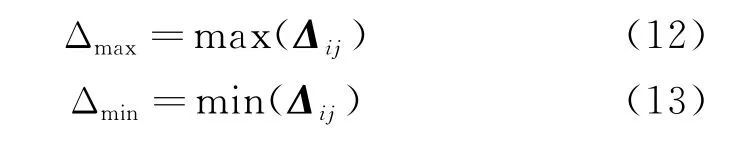
2.4 灰关联度系数矩阵的计算

关联系数可以表示成为：

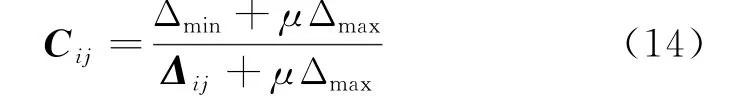
其中：μ为分辨系数.关联度Di可以表达成为：

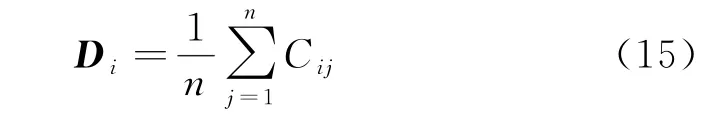
3 计算模型

计算模型选取广西某典型边坡体为工程实例，计算模型及模型网格如图1所示，一共剖分为675个单元，607个节点.设置上部，中部，下部监测点来实时监测计算过程中的温度、孔压及位移情况.

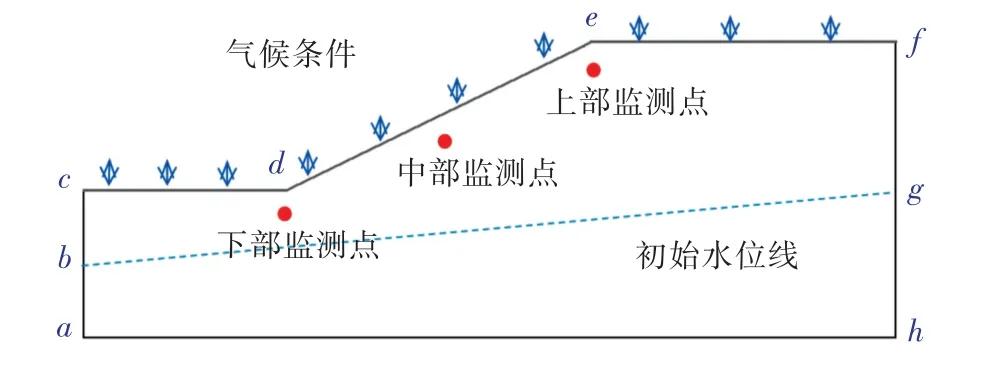
图1 计算模型

初始条件为图1(a)的初始水位线计算所得的初始孔压，其中ab，gf是水头边界，分别设置5m 和8m；cb、gf及af是零流量边界；cdef为综合的气候边界.

气候边界基于实测资料，如图2所示.

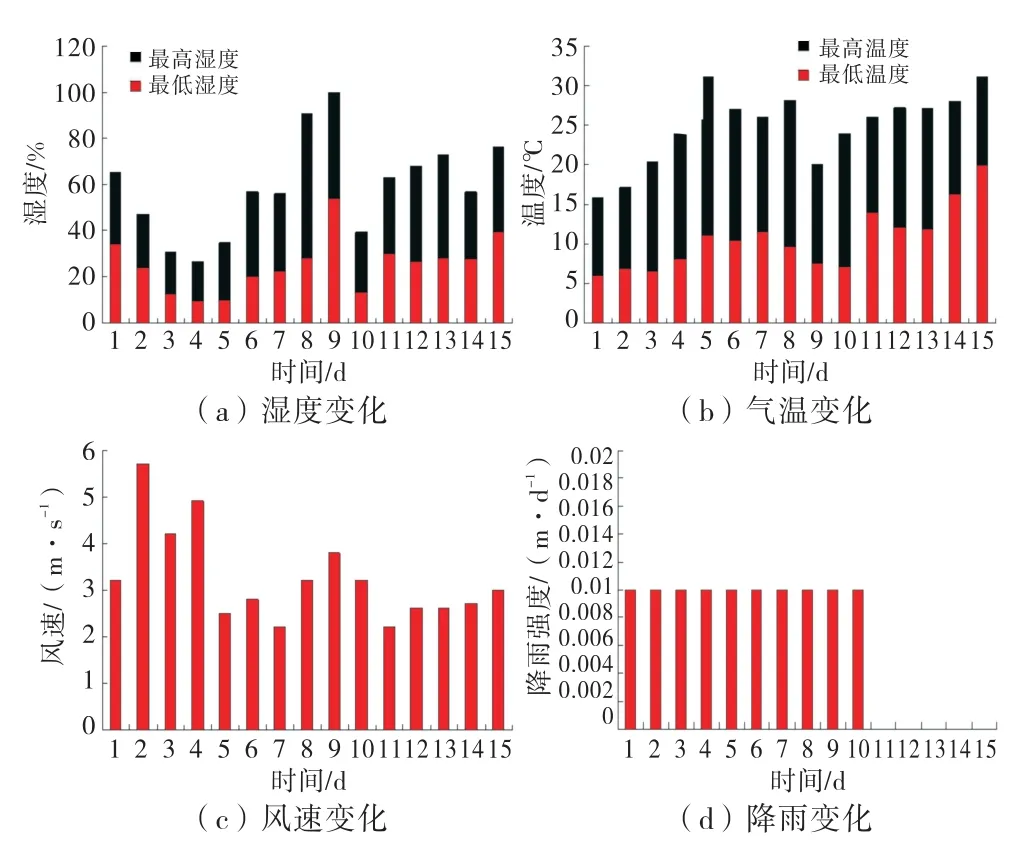
图2 边界变化

4 计算参数及工况

计算参数设置如下[9]：土体的渗透系数设置为0.6m/d；非饱和参数的进气值a=10kPa，拟合参数m=1，n=2.饱和体积含水量0.3m3/m3；热传导系数1875kJ/(m3·℃)；比热容是0.00176kJ/(g·℃-1)，导热系数函数曲线、体积-热容函数变化规律如图3所示.

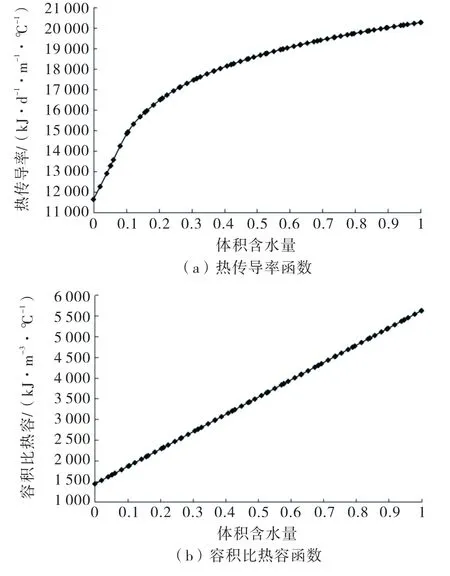
图3 热传导率函数及容积比热函数

计算工况为改变不同Fredlund & Xing参数k，a，m，n，工况设置如下：

1)a=5kPa，10kPa，20kPa，40kPa；m=1；n=2；

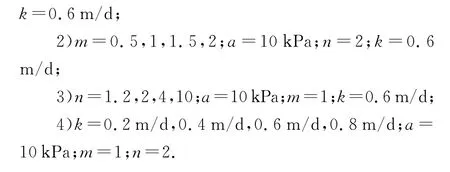
5 计算结果

5.1 不同监测点孔压变化

不同监测点的孔压变化规律如图4所示.

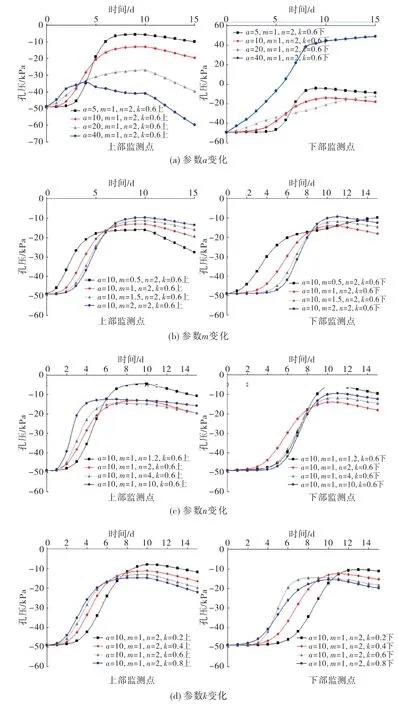
图4 孔压变化规律

由图4可知：降雨情况下边坡内部孔压不断升高，停雨后边坡表面发生蒸腾作用，孔压逐渐降低，但是在本文设定计算结束时刻的孔压仍大于初始孔压值.测点越靠近坡脚，孔压变化幅值以及整体孔压值大小均大于距离坡脚较远的测点.进气值a越大，前期测点孔压值上升越快，幅值也越大，但是孔压后期下降的速度也越快，幅值也越大.下部监测点在a值较小的时候(进气值a≤20kPa)时，a越小，前期孔压上升幅值也越小，但是孔压后期上升幅值较大，对于进气值a值较大情况下，边坡内部孔压较进气值a较小情况上升幅度大.拟合参数m值越大，前期孔压上升速率越慢，幅值也越小，但是孔压后期上升较快，幅度越大，测点越靠近坡脚，整体上孔压数值要大于远离坡脚的监测点.n值较小(n=1.2)时，前期测点孔压上升速率较慢，幅度较大，但是孔压后期上升较快，幅度也较大，在n值大于1.2的情况下，n值的不同引起的孔压差异并不大.拟合参数k值越大，前期测点孔压上升速率越慢，幅度也越小，但是孔压后期上升较快，幅度也较大.

5.2 不同监测点温度变化规律

不同情况下的测点温度变化如图5所示.

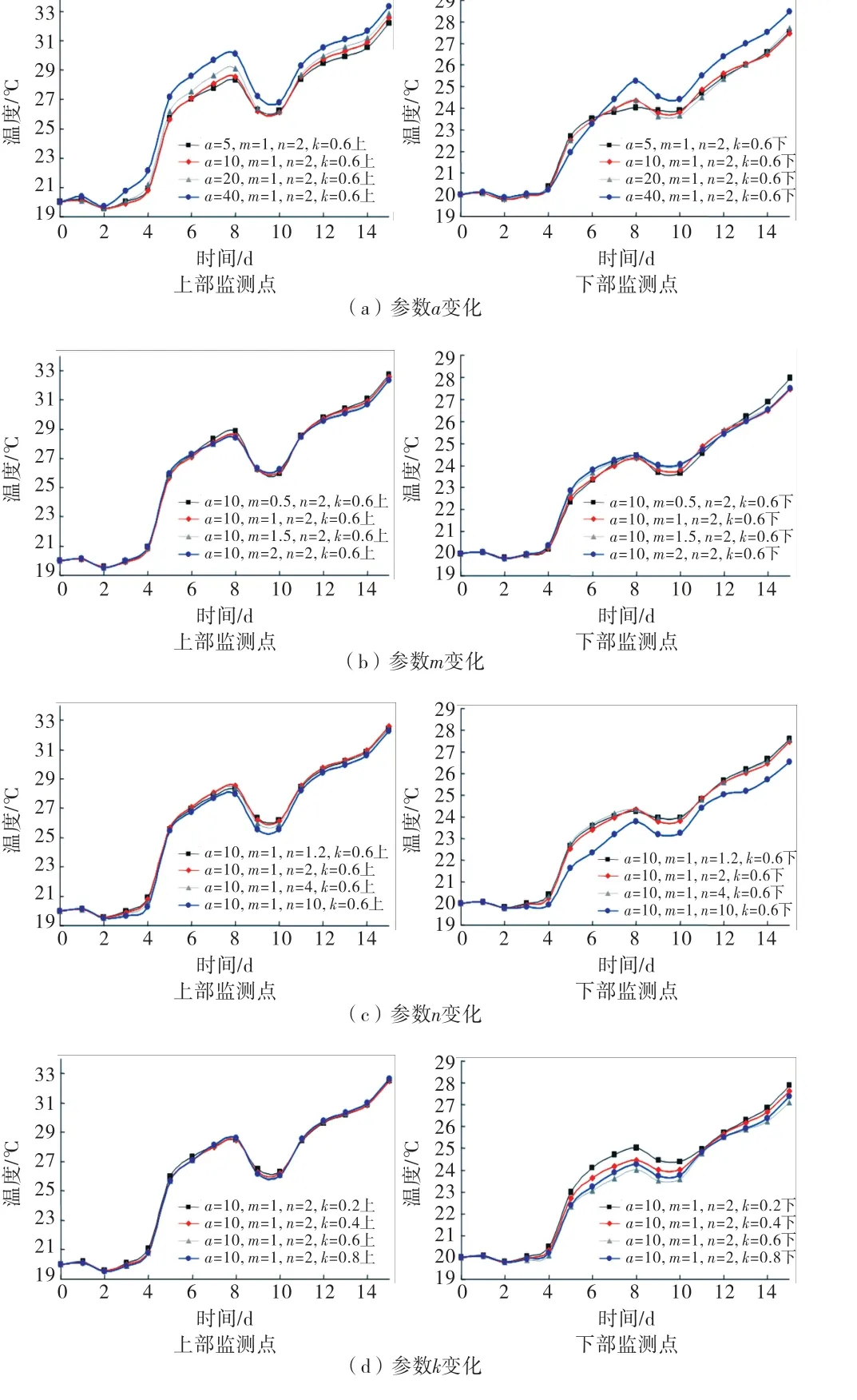
图5 温度变化规律

由图5可见，边坡内部不同监测点的温度变化规律与当地的气温变化的大体规律一致，不同非饱和参数对边坡不同监测点的温度变化略有影响，a值越大，m，n，k值越小，整体的温度越高，同时，监测点距离坡脚越近，温度变化幅度要大于远离坡脚的监测点.

5.3 不同情况下的监测点位移

不同监测点不同非饱和参数下的位移变化如图6所示.

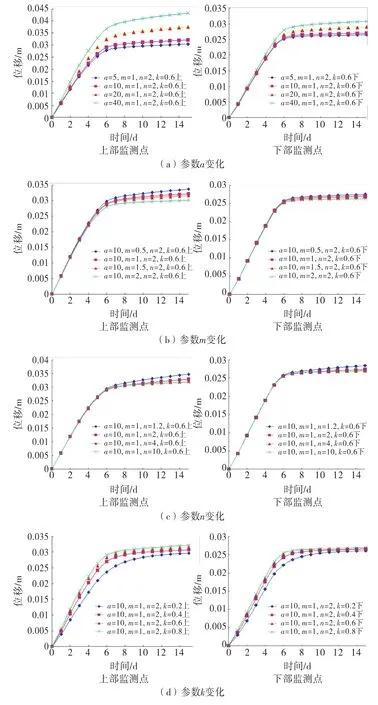
图6 位移变化规律

边坡变形较大发生在降雨前期，而残余变形则发生在降雨后期及停雨过后，变形较前期要小.对于不同非饱和参数下，降雨过程中的变形量的变化则不同，参数a对边坡在库水位骤降情况下的变形量影响最大，上部监测点的最大变形量在3.1～4.8cm 之间，下部监测点的最大变形量在2.7cm～3.4cm 之间；参数m，n，k则影响较小，上部监测点的平均最大变形量在3.1～3.3cm 之间，下部监测点的平均最大变形量在2.7～2.9cm 之间.

5.4 边坡安全系数

边坡安全系数变化如图7所示.降雨条件下安全系数呈现单调下降的规律，降雨前期安全系数迅速下降，降雨后期安全系数缓慢下降，这与本文第5.3节中的边坡监测点位移计算规律一致.参数a与参数k变动对稳定系数的变幅影响较大，其中当参数a=5时最小稳定系数为0.99，说明此时边坡处于失稳的状态，而参数m与参数n对稳定系数的变幅影响较小.

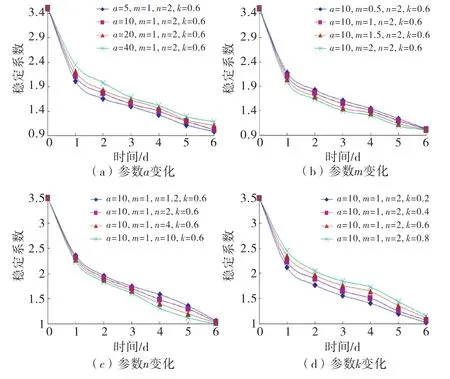
图7 安全系数变化规律

6 灰关联度敏感性分析

对不同参数变动下的边坡渗透稳定性根据式(10)～(20)进行灰色关联度敏感性分析.对不同非饱和参数a，m，n，k变化情况下的上部、中部及下部位移情况及最小安全系数统计见表1.

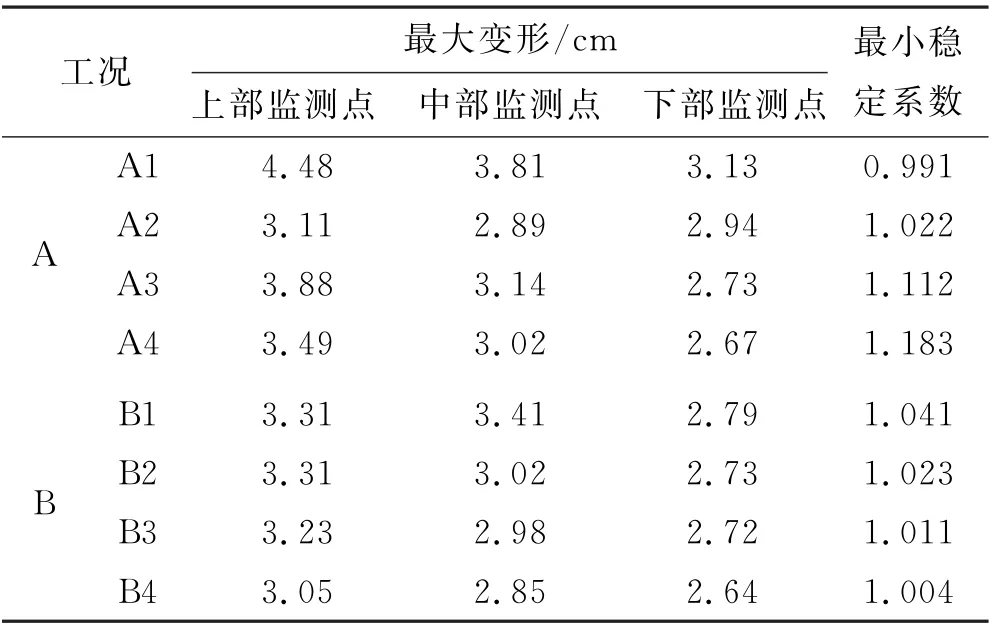
表1 不同工况变形及稳定系数

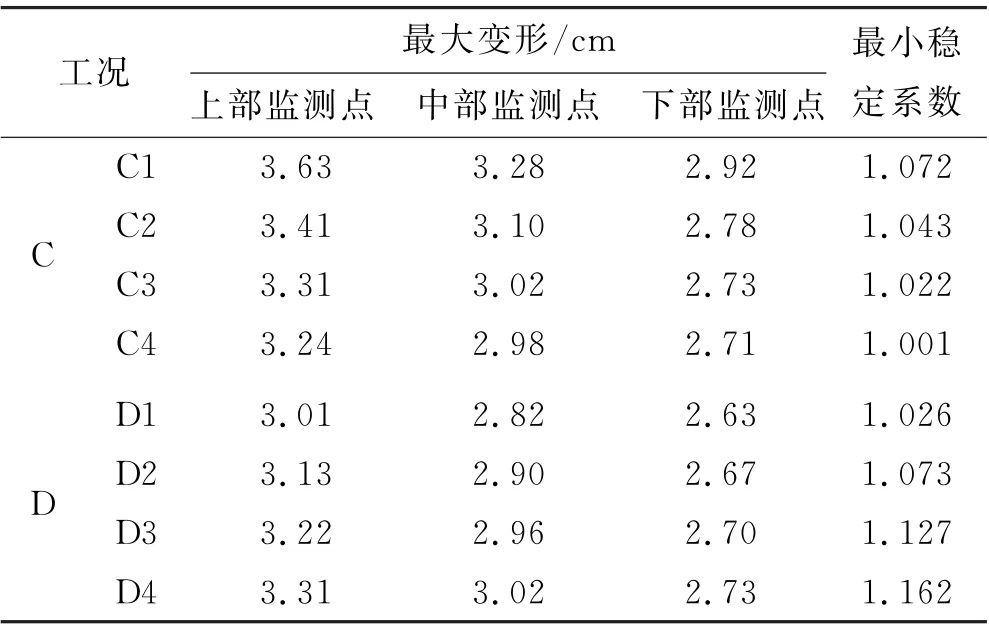
续表1 不同工况变形及稳定系数

可以得到会关联度系数矩阵如下：

关联度矩阵可以根据式(14)求出：

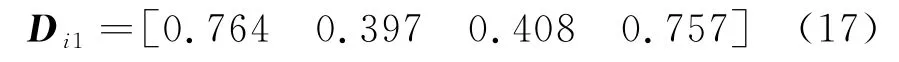
汇总灰关联系数表见表2.由表2所示，对于本文所分析的参考指标(上部监测点，中部监测点，下部监测点与最小安全系数来说)参数a与参数k对降雨工况下的边坡渗透稳定性影响较大，而参数m与参数n影响较小.

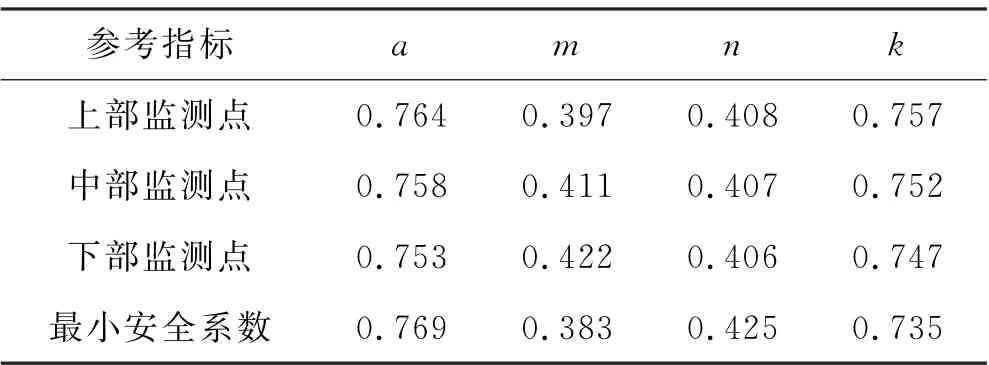
表2 汇总灰关联系数表

7 结 论

1)不同监测点在降雨过程中孔压呈现不断增大的趋势，停雨后由孔压逐渐回落，检测点越靠近坡脚，孔压上升幅度以及整体上的孔压值均大于远离坡脚的监测点，a值，n值越大，孔压前期上升越块，而在后期上升越慢，m，k则刚好相反.

2)温度变化趋势与气候条件下的温度变化较为一 致，a值 越 大，m，n，k值 越 小，整 体 的 温 度 越 高.

3)边坡位移与安全系数在降雨前期变形较大，而在降雨后期及停雨过后较小，参数a与k对边坡位移影响较大，而参数m，n影响则较小.

4)对考虑蒸发条件下的边坡温湿耦合情况下的渗透稳定性规律进行了灰关联度敏感性分析，得到了上部监测点，中部监测点与下部监测点与安全系数的灰关联度系数，参数a与参数k对降雨工况下的边坡渗透稳定性影响较大，而参数m与参数n影响较小.