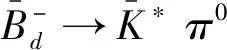因子化框架下同位旋破缺效应对CP破缺的影响

吕 刚，刘良辰，李秋实，王 莹，霍志鹏，韩江凡，彭 娜

(河南工业大学理学院，河南 郑州 450001)

CP破缺的测量是理解标准模型(SM)和探索新物理信号的一个重要领域。CP破缺来自于弱相角和强相角，由于夸克味道的混合，Cabibbo-Kobayashi-Maskawa (CKM)矩阵为其提供了弱相角。但强相角来源于量子色动力学和其他机制，可以通过一些新的机制来改变强相角，从而改变CP破缺的数值，同位旋破缺的π0-η-η′混合可以提供新的强相角。基于这种考虑，本文在简单因子化框架下，研究了B→P(V)π0衰变过程中同位旋破缺效应对CP破缺的影响，为国际大型强子对撞机实验提供理论依据。

1 计算与结果

1.1 有效哈密顿量

由算符乘积展开，△B=1的B介子弱衰变过程有效哈密顿量可表示为[1]：

(1)

1.2 同位旋对称性破缺效应的CP破缺

1.2.1 形式

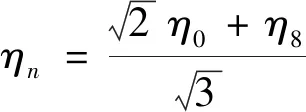
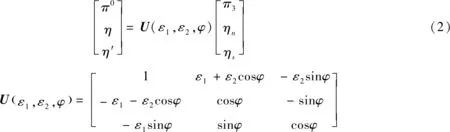
(3)

ε1,ε2∝O(λ)，λ≪1和高阶项被忽略。在同位旋极限ε1→0,ε2→0时，可以发现式(3)可表示为方程中的η-η′混合：

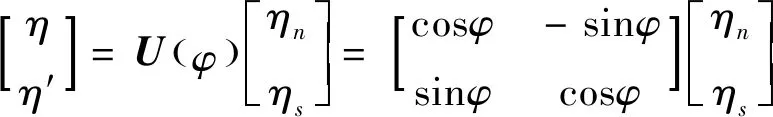
(4)

其中φ是混合角[3]。

相关的衰变常数可以写成[4-5]：

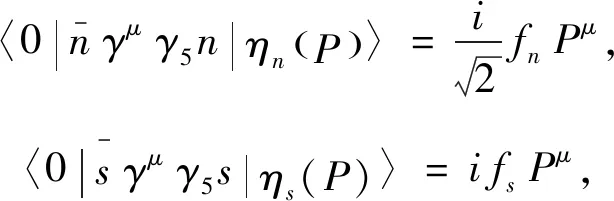
(5)

其中P是指ηn或ηs的动量。可以理解为同位旋对称性破缺是由标准模型中的电弱相互作用和u-d夸克质量差引起的。而且可以通过手征微扰理论计算同位旋对称性破缺校正，从而得到π0-η-η′混合。对于同位旋对称破缺的领头阶，式(2)、式(3)的物理本征态π0，η和η′可以写为[6]：

|π0〉=|π3〉+ε1+ε2cosφ|ηn〉-ε2sinφ|ηs〉

|η〉=(-ε1-ε2cosφ)|π3〉+cosφ|ηn〉-sinφ|ηs〉

|η′〉=-ε1sinφ|π3〉+sinφ|ηn〉+cosφ|ηs〉

(6)

其中ε=ε2+ε1cosφ，ε′=ε1sinφ。π3是指三重态中的同位旋I=1分量。使用的值为ε=0.17±0.002，ε′=0.004±0.001，φ=39.0°[2]。

1.2.2 计算过程

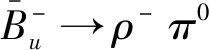
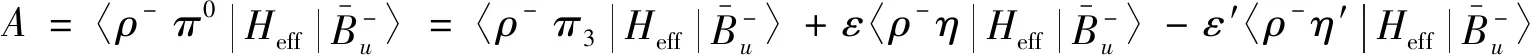
(7)

此时π3表示I=1的I3=0的三重态，即π0。

(9)

其中HT和HP是哈密顿量中的树图和企鹅图算符。

HT和HP的相对振幅和相角可以表示为：

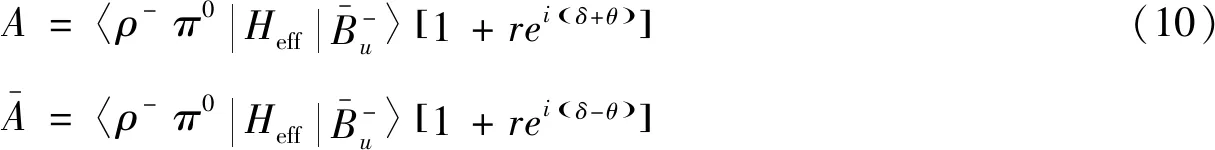
(11)

其中δ和θ分别为强相角和弱相角，相关的弱相位和强相位获得如下[6]：

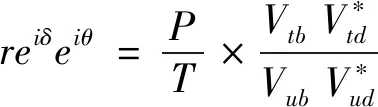
(12)

参数r表示企鹅图和树图振幅比值的绝对值：

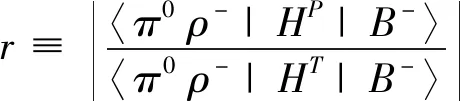
(13)

与r相关的强相角可以给出：

(14)

其中，

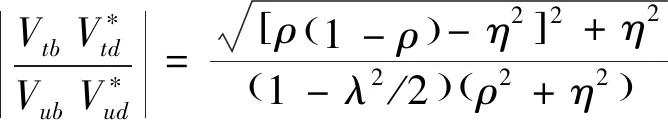
(15)

其中，ρ，η，λ是Wolfenstein参数。

CP破缺的参数表示为：

(16)

1.2.3 数值结果

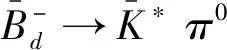
表1 同位旋对称性和同位旋对称性破缺π0-η-η′混合的CP破缺数值Tab.1 CP breaking values for isospin symmetry and isospin symmetry breaking π0-η-η′ mixture

2 结论