VSG控制参数对系统频率稳定性的影响分析

夏正邦，李培强，李俊男，林 穿，商俊杰

(1.福建工程学院信息科学与工程学院，福建 福州 350118；2.智能电网仿真分析与综合控制福建省高校工程研究中心，福建 福州 350118)

新能源发电技术是当今世界能源发展的新目标，因其不会排放二氧化碳引起温室效应，也不存在燃油、燃煤的空气污染问题，故而具有绿色、环保的优点。但新能源发电在受到负荷的扰动和出力的波动时会影响系统的稳定性，虚拟同步机是实现新能源友好并网的关键技术[1-2]。虚拟同步发电机不同的控制参数对系统动态稳定性的影响是不同的。为了更全面地应用虚拟同步发电机技术, 有必要探究这些因素对电力系统频率稳定性的影响规律。

在微电网领域VSG是参与电网电压幅值、频率调节的控制策略，能在大功率缺失情况下对提高系统电压和频率发挥出应有的作用[3-4]。采用虚拟同步机控制的可再生能源发电协同储能装置模拟传统同步发电机的外特性, 使得逆变电源对外输出具有一定的惯性和阻尼，体现了VSG控制算法的优势[5-6]。文献[7]建立了单机三相无穷大电源系统算例，虚拟发电机控制技术能快速响应负载功率变化，改善系统频率变化幅值。文献[8-10]建立VSG转子机械方程的小信号建模，根据根轨迹分析同步电抗、阻尼系数、线路参数、负荷参数等参数对系统稳定性和动态性能的影响规律，并利用VSG带RL负载的工作模式进行系统仿真验证。目前相关文献对VSG的稳定性问题进行了一定的研究，但考虑的参数不全，而且仿真的工况较少。

本文首先建立VSG各环节的数学模型，建立系统的小信号模型，分析关键控制参数变化时的根轨迹，探究其对系统稳定性的影响规律，为控制参数的选取提供依据。仿真比较分析了虚拟同步机与下垂控制之间频率响应特性的差异，最后研究了VSG在孤岛独立运行、参考功率变化和负荷扰动3种不同工况下对控制参数理论分析进行了仿真验证，仿真结果证明了理论分析的正确性。

1 虚拟同步机的基本原理

1.1 虚拟同步发电结构模型

同步发电机定子电压方程可表示为：

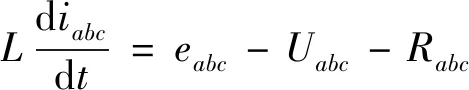
(1)

式中的eabc为内电势，Uabc为机端电压，Iabc为相电流。

电磁转矩Te和虚拟同步机的电磁功率Pe之间的关系为：

(2)

1.2 虚拟同步机控制原理

VSG控制通过借鉴同步发电机中的调速器作用模拟一次调频特性、同步发电机的转子运动方程来模拟转动惯性和阻尼特性以及励磁控制器来模拟无功—电压下垂特性，使得电力电子逆变器具备一定的惯性和阻尼，能够具有参与电网调频和调压的能力。VSG控制框图如图2所示，其使用三相电压型逆变器与微电网相连。整体控制策略由频率控制、电压控制、阻抗环节和双电控制组成。其控制算法过程如下：实时采集虚拟同步发电机并网端输出电压Uabc和电流信号Iabc，系统自动计算得到Udq、电压幅值Um和Pe，并通过功率计算模块和幅频运算得到系统实际的无功功率Q和系统角频率ω0；将这些信号传送至有功频率控制器和无功电压控制器中，获取VSG控制算法的输入信号虚拟同步发电机的角度θ、励磁电动势E0、Iabc、ω0和Udq，通过内部虚拟同步发电机算法得到并网电压指令值U*，将该值作为SPWM调制信号波，从而得到并网逆变器的驱动信号控制逆变电源；最终通过逆变器控制储能系统发出或吸收的功率，使得系统能够保持功率平衡，从而实现提高系统稳定性的作用。

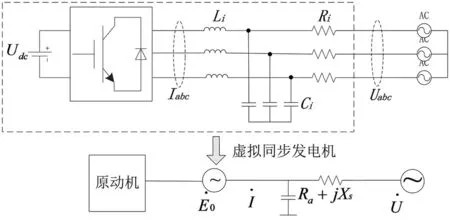
图1 逆变器虚拟同步发电机的等效模型Fig.1 Synchronous generator structure simplified diagram

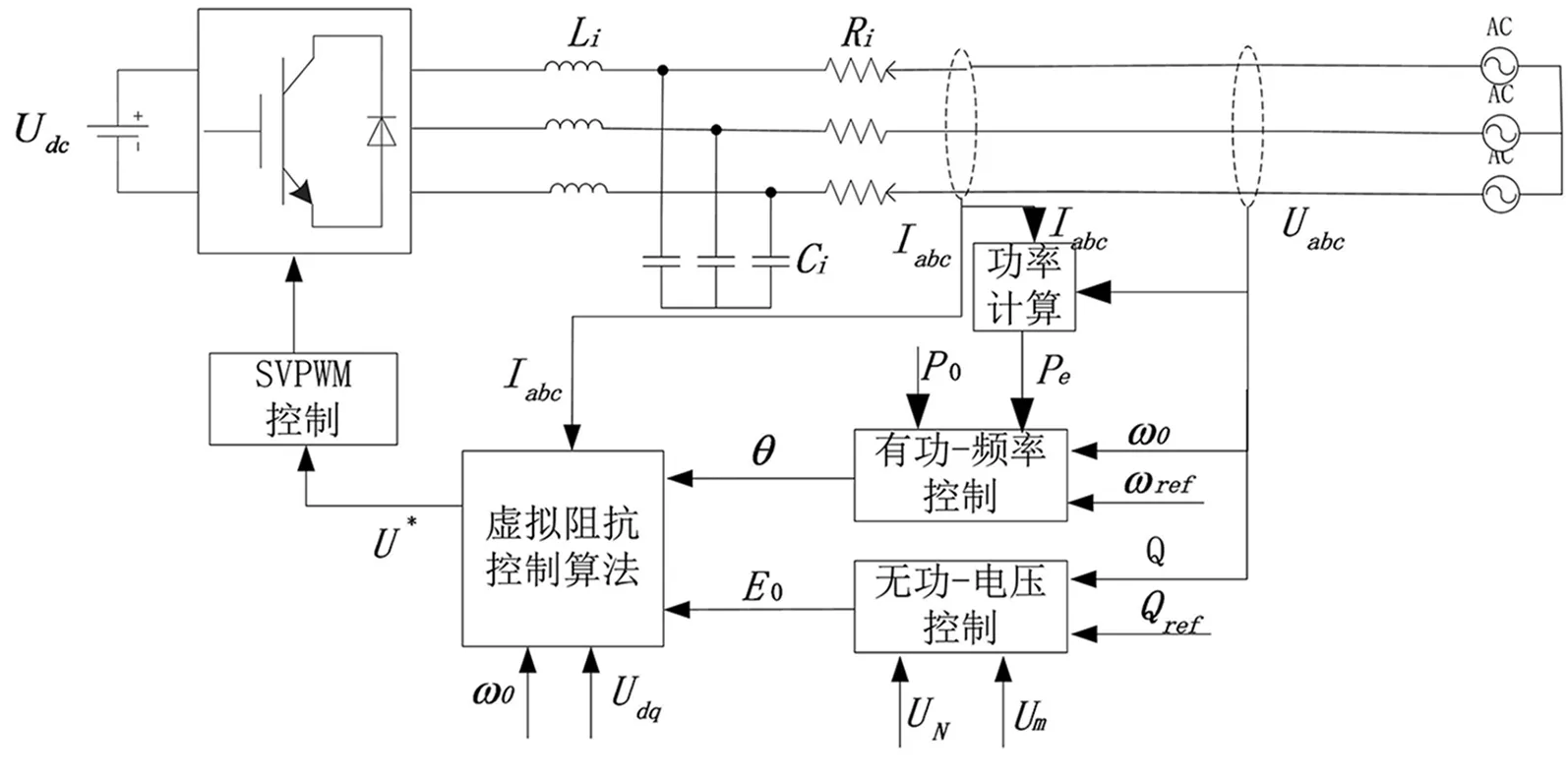
图2 虚拟同步发电机控制框图Fig.2 Virtual synchronous generator control schematic

1.3 功频控制器

在电力系统运行中,同步发电机内部的调速器会根据频率的偏差量、控制原动机的输入量并改变机械功率的大小。通过调控发电机转速使系统有功功率重新达到平衡工作状态，实现电力系统的一次调频。参考同步发电机的调速器原理，设计一个有功—频率控制环节，能根据反馈系统频率变化率，可以补偿系统中的不平衡能量，

根据ω=pΩ,当极对数P为1时，转子运动方程可表示为：

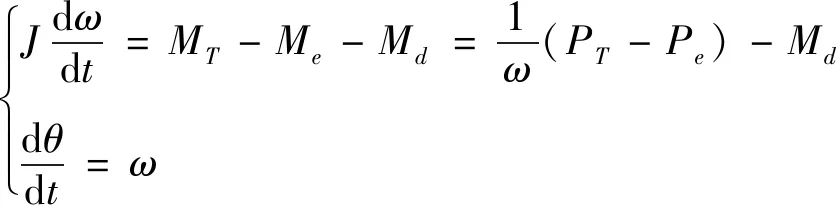
(3)

式中PT、Pe分别为机械功率和电磁功率，J为转动惯量，MT为机械转矩，Me为机械转矩，Md为摩擦和损耗转矩，ω为机械角速度，电角度θ为ω经过积分得到。

将机械方程式变形为：

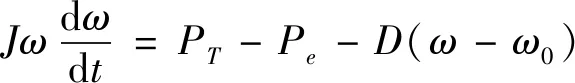
(4)

综合转子运动方程和调速器方程，得到VSG功频控制的方程式：

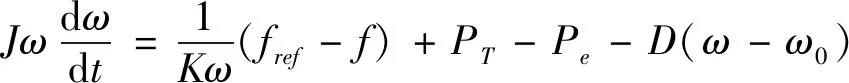
(5)

根据式(5)设计的功频控制器如图3所示。

图3 功频控制器Fig.3 Power frequency controller

根据式(4)和式(5)，P-ω的传递函数可以写为：

(6)

进一步整理得到变化的系统频率和有功功率之间的关系如下：

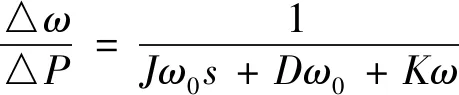
(7)

2 虚拟同步发电机关键参数分析

2.1 J和D的影响分析

同步发电机正常运行时，一部分动能以电能形式输送出去，剩余动能由于转子的高速旋转以转动惯量形式体现出来。当系统受到扰动时，转子能够继续存储和释放动能，转动惯量起到了缓冲的效果，同时达到有效抑制频率迅速波动的目的。以电力电子元件为基础的逆变器动态响应迅速，几乎没有任何惯性。因此，当大量以逆变器为基础的新能源系统连接到电网中，它们对负荷的变化特别敏感，即使负荷产生微小的变化，也会导致电力系统的频率产生非常大波动，对逆变器带来冲击进而引起逆变器故障，对电网的稳定也十分不利。

将虚拟同步发电机的惯性用虚拟惯量J来表达：

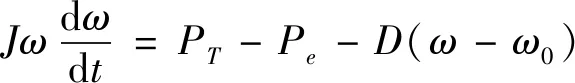
(8)

以同步发电机为例，当受到负荷扰动时，会破坏原有的功率平衡，造成功率差额。然后，同步发电机的调速器开始动作，通过改变输出的机械功率以补足功率差额。而调速器的惯性作用使得调节具有滞后性，同步发电机不能立即根据负荷的变化输出功率，同时发电机上的转矩不相等会造成转速的变化，并引起系统功率的波动和频率的变化。根据式(8)等式右边不变的情况下，由于转动惯量J的存在，角频率变化率会变小，且J越大，角频率变化率会越小，J对转速变化具有约束作用。对于传统逆变器来说，J几乎为0，对系统转速调节没有滞后性，导致功率变化快会给逆变器带来很大的冲击。不过引入了大惯量特性的VSG控制算法，可以使逆变器可以具有和同步发电机类似的动态特性，有效抑制电网内由于负荷扰动引起的频率波动，提高了系统频率的稳定性。

当电力系统进入稳态时，角速度变化率等于零，式(8)变为：

△T=D(ω-ω0)

(9)

可见阻尼系数D主要影响系统频率的变化量，可以有效地逐渐下降振动幅度，防止在负荷突变下导致不平衡转矩，频率发生较大的波动下使VSG能够尽快恢复到稳定运行状态。下面建立VSG控制的小信号模型，更好说明参数J和D对系统控制性能的影响。

2.2 小信号模型的建立

为了探究VSG控制中主要控制参数对系统频率稳定性的影响规律，因此有必要对VSG控制进行建模。

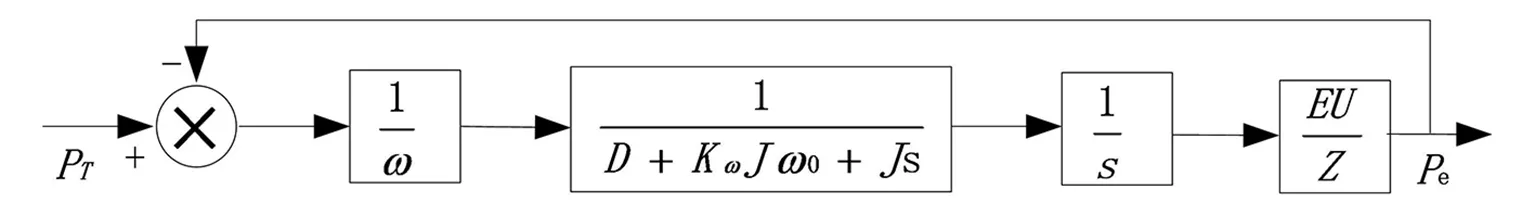
图4 VSG小信号模型Fig.4 Small-signal model of VSG

由小信号模型可以得出逆变器输入输出有功功率的传递函数：

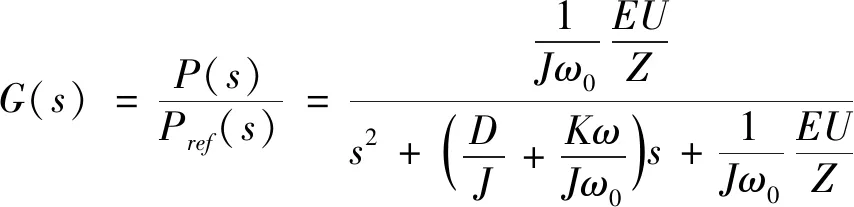
(10)

其为典型的二阶传递函数,对应的自然震荡角频率ωn和阻尼系数ξ为：

(11)

二阶系统动态性能由J、阻尼系数D和调差系数Kω决定，一般Kω恒定，当D恒定时，J越大，ξ越小，调节时间越长; 当J恒定时，D越大，ξ越大，调节时间越短。通常为了减少超调量和调整时间，转动惯量J不能过大。

系统特征方程为：

(12)

等效开环传递函数：

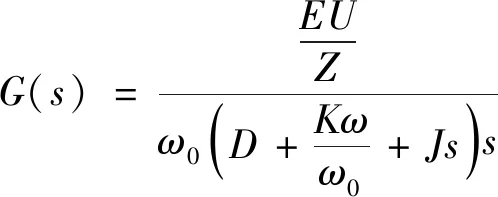
(13)

2.3 控制参数对系统稳定性的影响

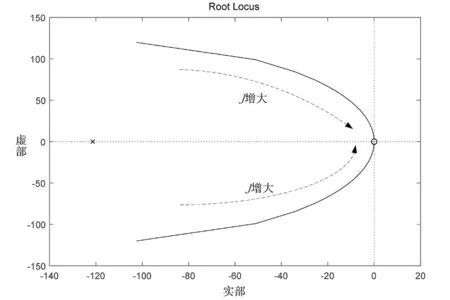
图5 J增大时的根轨迹图Fig.5 Root locus when J increases

开环传递函数涉及J、D和Kω3个变量，为了分析判断其对系统稳定性和动态性能的影响，可以根据建立的等效开环传递函数绘制出不同参数变化时的根轨迹图来表示。取内电势E等于240 V,电网相电压有效值220 V，虚拟阻抗Z为(1+j2)Ω，额定频率50 Hz。

当D取20和Kω取10 000时，虚拟惯量J不断增大时，系统的特征根轨迹如图5所示。J的存在会对系统的稳定性有改善作用，J越大，开环极点越接近坐标原点，系统的稳定性逐渐变差，说明参数J的变化对系统稳定性具有一定影响，但转动惯量的选取不能过大。

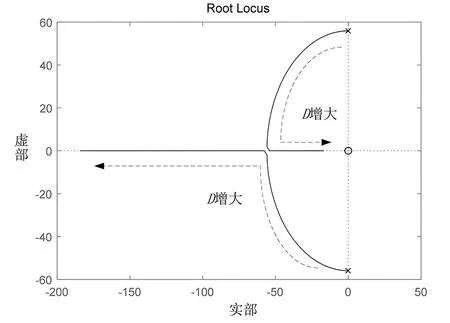
图6 D增大时的根轨迹图Fig.6 Root locus diagram when D increases

当J取0.5和Kω取10 000时，阻尼系数D不断增大时，系统特征根轨迹如图6所示。特征根在虚轴上，系统处于临界稳定状态，受到扰动时将会失去稳定，从另一个角度说明了阻尼参数的意义。随着D的不断增加，系统的阻尼比也会不断增加，但其中一个特征根也将不断靠近虚轴，系统的稳定性开始恶化。

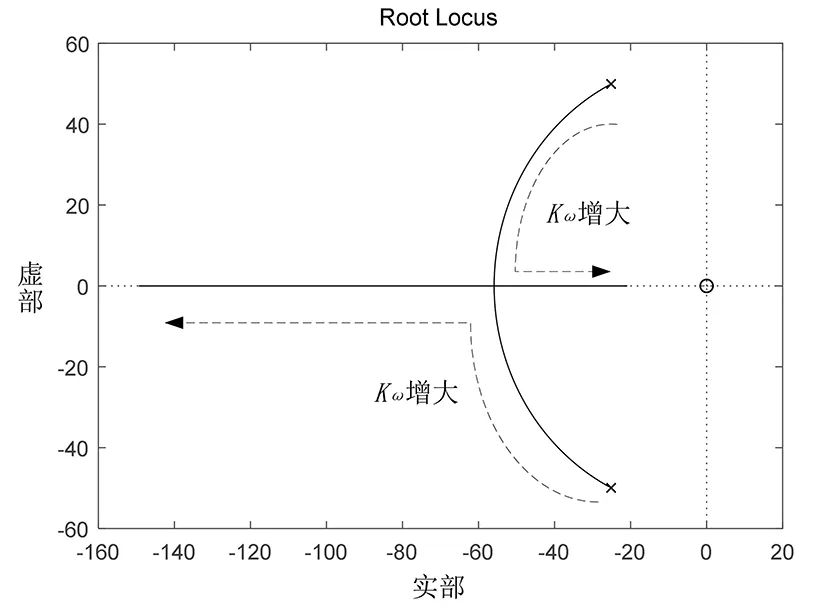
图7 Kω增大时的根轨迹图Fig.7 Root locus graph when Kω increases

当J取0.5和D取20时，调差系数Kω不断增大时，系统的特征根轨迹如图7所示。当D和J不变时，Kω值较小时，增加Kω的值，根轨迹逐渐向左侧移动，系统的稳定性逐渐提高；Kω继续增大，根值随着箭头方向移动到实轴，系统处于过阻尼状态并开始在实轴上以相反方向移动，导致稳定裕度减小。

因此，控制参数J、阻尼系数D和调差系数Kω的设计和选择对于VSG控制策略的实现至关重要。当J为恒定值时，阻尼系数D或Kω太小或者太大都将降低系统的稳定性，因此有必要适当选择D或Kω的值。在设计时也会结合不同的控制效果综合考虑诸如低频振荡、动态响应时间等因素，以满足系统稳定性的要求。

3 算例仿真验证

以上采用小信号分析方法对主要控制参数系统稳定性的影响进行了探讨，为了验证本文虚拟同步发电机组控制策略及参数设计的正确性，根据图2,在Matlab/Simulink上建立了模型进行分析验证。三相电源额定电压380V，系统频率为50Hz。VSG相关的参数如下表1，参数可根据系统运行工况灵活选取。

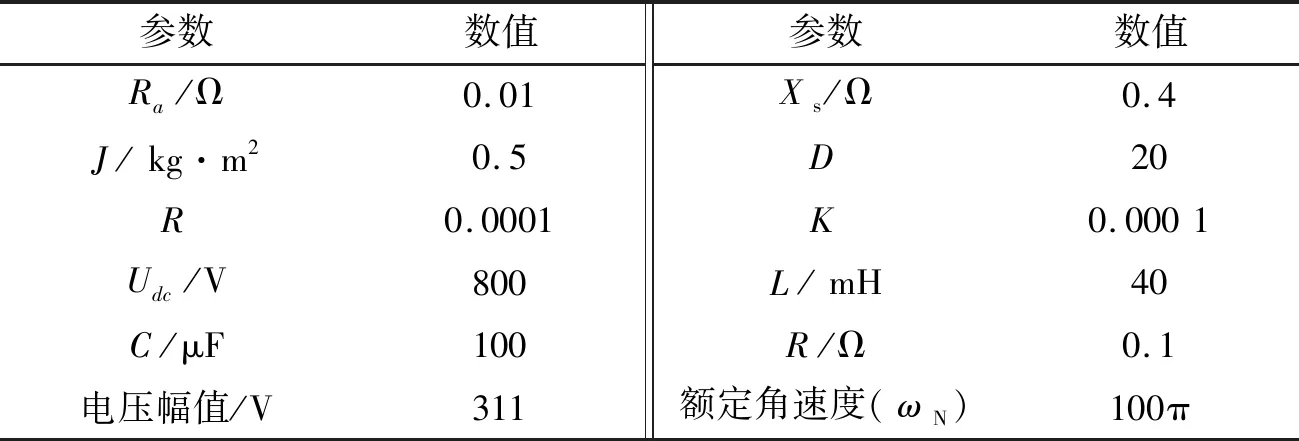
表1 VSG本体参数设置Tab.1 VSG parameter setting

3.1 与传统下垂控制对比分析

将VSG与下垂控制在孤岛带负荷工况下进行仿真对比，直观的比较两者在负荷扰动时频率的差异。在仿真对比中，VSG中的控制参数Kω=10 000、J=0.5和D=20，孤岛模式运行下，在0.5 s时，突加2 kW的负载，在1 s时，减少4 kW的负载，负荷有功功率变动如图8(b)所示，频率响应曲线如图8(a)所示。下垂控制在负载变化后，系统的频率下降速度较快，响应迅速，而由VSG控制的系统其频率变化过程比较缓慢，但一段时间后都将稳定在相同的额定频率值。由此可见，下垂控制下的频率瞬时响应，而VSG在惯性作用延缓了频率的下降速度频率缓慢响应，虚拟同步发电机控制中转动惯量可以提高系统频率的稳定性。

3.2 虚拟同步发电机对频率的调节特性

VSG孤岛带载运行时，VSG的输出有功功率和频率是由负载大小决定，逆变器的输出功率随着负荷功率变化而变化，频率跟着发生变化。系统运行时，在1 s和2 s时分别投入和切除负载。当D=20和Kω= 10 000，分别令J= 0.5、1、2进行仿真运行；当J=0.5和Kω= 10 000，分别令D=5、10、20进行仿真运行；当为D=20和J=0.5不变，分别令Kω= 10 000、20 000、40 000进行仿真运行。VSG的频率变化曲线如图9所示。从仿真结果可以看出，频率的变化与上述分析一致。当D和Kω一定时，J越大，惯性响应时间越长，系统的频率变化越缓慢；J和Kω一定时，随着D的增大，频率变化幅度越小，D每增加一倍，频率变化量大约减少0.25 Hz；J和D一定时，随着Kω的增大，频率变化幅度越小，Kω每增加一倍，频率变化量大约减少0.05 Hz。

图8 VSG控制和下垂控制的对比仿真Fig.8 Comparative simulation of VSG control and droop control

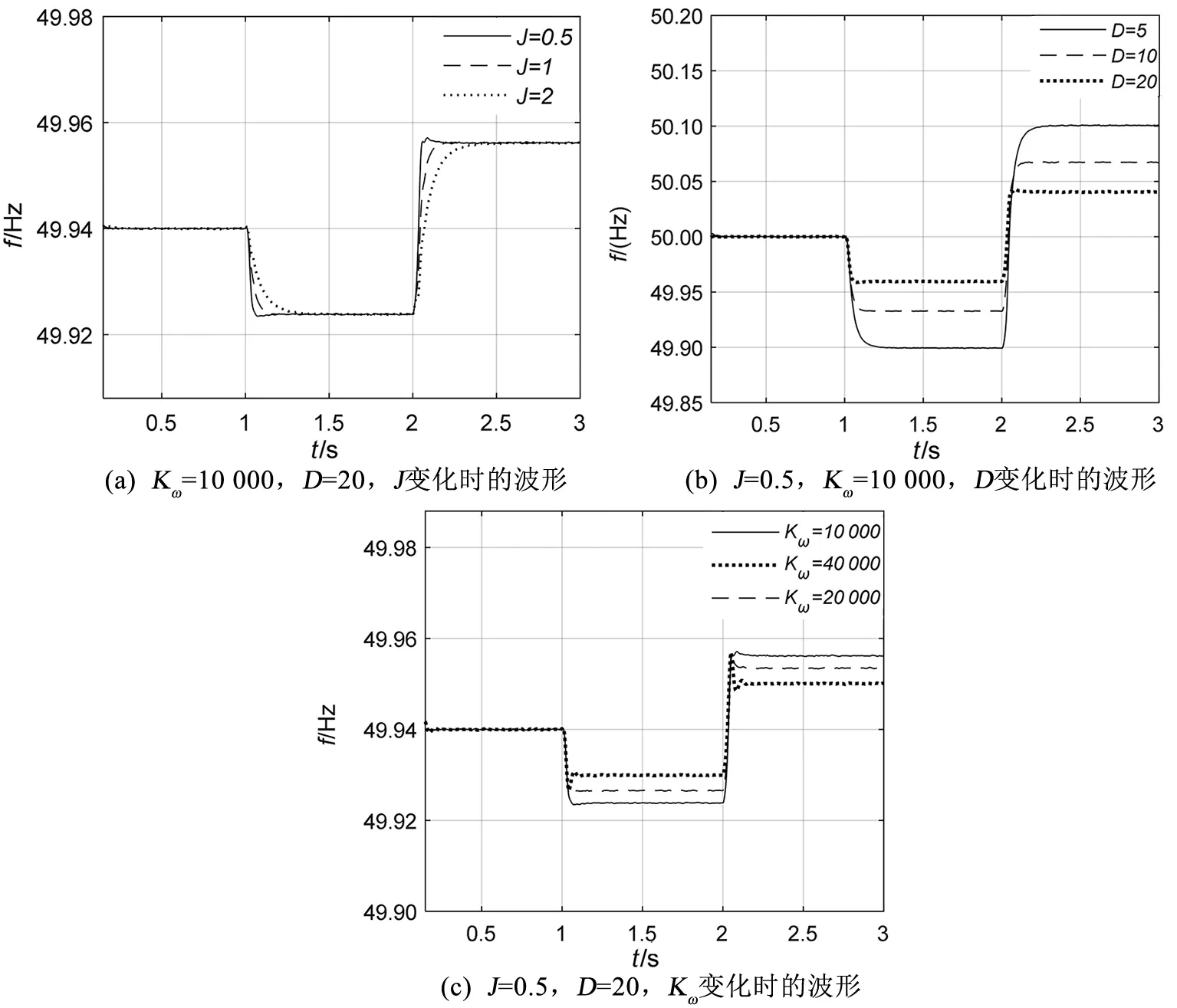
图9 参数不同时对应的频率波形Fig.9 Frequency waveforms corresponding to different parameters

3.3 VSG的输出功率调节对电网频率的影响

VSG与无穷大电源连接运行时，分析VSG的输出特性。1.5 s和3 s时分别将VSG输入功率的参考值设置为20 kW和10 kW。当D=20和Kω=10 000，分别令J=0.5、1、2进行仿真运行；当J=0.5和Kω=10 000，分别令D=5、10、20进行仿真运行；当为D=20和J=0.5，分别令Kω=10 000、20 000、40 000进行仿真运行。以上分析与所述轨迹图分析及仿真结果相吻合，VSG频率响应过程如图10所示。

图10 参数不同时对应的频率波形Fig.10 Frequency waveforms corresponding to different parameters

J值在0.5、1和2时的频率最低值分别为49.90、49.92和49.92 Hz，最高值分别为50.19、50.16和50.14 Hz，不同的J常数下，表现出不同的惯性大小对系统的频率调节也不同，即J越大，减少了系统频率的变化幅值，对系统有功频率的支持作用越明显；但随着数值的增加到2附近时，分布式电源系统的动态响应速度变缓，超调量也逐渐增加，并产生了振荡；D值在5、10和20时的频率最低值分别为49.83、49.87和49.91 Hz，最高值分别为50.32、50.25和50.20 Hz，不同的D常数下，表现出不同的阻尼大小对系统的频率调节也不同，即D越大，减少了系统频率的变化幅值，对系统有功频率的支持作用越明显，且频率变化的越缓慢；Kω值在10 000、20 000和40 000时的频率最低值和最高值时差距不大，但Kω越大，系统的动态响应速度变缓，超调量也逐渐增加，并产生了振荡。VSG进行调节后，输出频率都能恢复到50 Hz。因此在并网运行时，J取值范围为1～2，D为20时最好，Kω值在20 000和40 000之间。

3.4 负荷扰动时VSG的输出频率调节

为了分析并网运行模式下系统负荷发生变化时VSG的输出特性，仿真运行时，在2 s和3 s时，分别设置了负荷突减和突增扰动，当D=20和Kω=10 000不变，分别令J= 0.5、1、2进行仿真运行；当J=0.5和Kω=10 000不变，分别令D=5、10、20进行仿真运行；当为D=20和J=0.5不变，分别令Kω=10 000、20 000、40 000进行仿真运行。并网负荷扰动下，VSG输出的频率响应变化与上一节基本一致，其效率响应过程如图11所示。

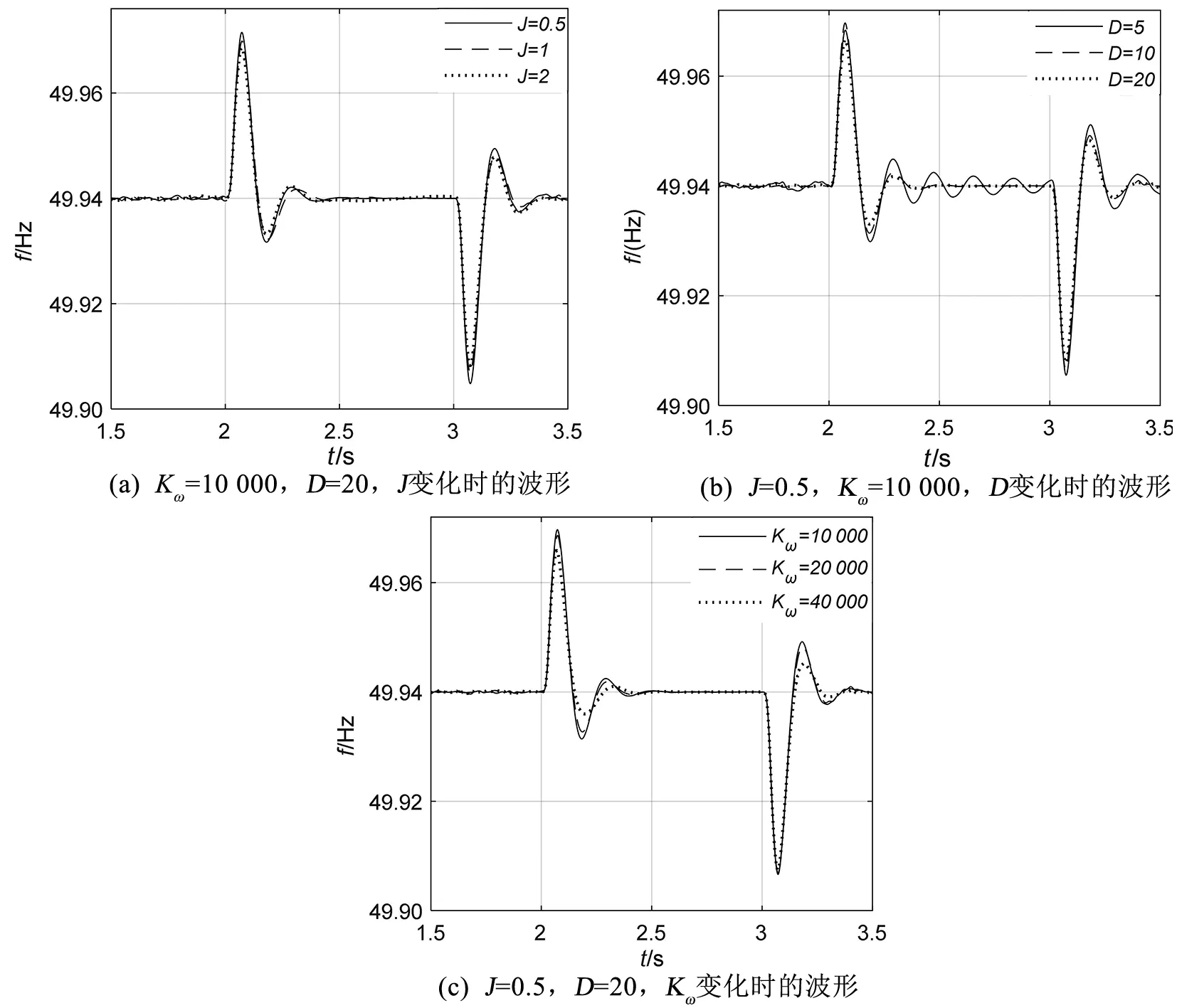
图11 不同参数对应的频率波形Fig.11 Frequency waveforms corresponding to different parameters

4 结语

本文首先针对VSG控制中关键控制参数进行研究，给出了惯性、阻尼和调差系数参数的数学模型，建立了逆变电源的小信号模型，并探讨了其对系统动态稳定性的影响规律。然后将所提出的VSG控制和下垂控制算法进行比较，从而对比出VSG控制算法的优点。最后针对3种不同工况进行了仿真验证，进而得到对频率稳定性的影响规律，总结了关键参数的选取原则。通过仿真分析，可以得到如下结论：

1) 与传统的下垂控制策略对比下，可以看出VSG控制策略能增大系统等效惯量的优点,VSG由于惯性的存在其频率响应的动态特性更好。

2) VSG的动态稳定性受控制参数的影响较大，J可以增大系统的惯性，系统参数D和Kω值的增加可以减小频率下降的幅度，但同时会增加超调量和调节时间，进而导致不稳定。因此在孤岛运行时，3个变量的取值可以适当大些；但在并网运行时，J取值范围为1～2，D为20时最好，Kω值在20 000和40 000之间。可以根据具体的要求来制定虚拟同步发电机相关控制参数。