随机五边形网格螺旋链图的ABC指标和GA指标
2020-05-29胡晓婷魏首柳余倩倩
胡晓婷,魏首柳,谢 丹,余倩倩
(闽江学院数学与数据科学学院,福建 福州 350108)
图的拓扑指标是基于图中顶点的度、边与边、顶点与顶点之间的连接情况,是图的一种不变量及分子结构数值化的一种方式,将分子结构抽象成数字反映分子的拓扑特征.它直接衍生于化合物结构图的数学不变量,依赖于化合物的分子结构。拓扑指标不但可以定量地描述化合物的分子结构,也可以分析相关分子的结构和性能之间的关系。分子拓扑结构的描述确定了分子的许多特性,除了包括那些与分子大小和形状有关的性质外,还包括分子的量子力学特性,特别是在定量结构—属性关系(QSPR)和定量结构—活动关系(QSAR)的研究中得到了广泛应用。 因此,给出反映分子结构基本特征的一种定量标准(度量)在化学图论中具有重要意义。从Wiener提出第一个分子拓扑指标即Wiener指标之后,已有数百种分子拓扑指标出现在各种不同的文献中[1-2]。 Gutman在文献[3]中全面总结归纳了基于度的各种拓扑指标的计算表达式和相应的历史背景,其中最著名的有Randic指标、Wiener指标、Merrifield-Simmons指标、Zagreb指标、Atom-bond Connectivity指标(ABC指标)和Geometric-arithmetic指标(GA指标)等。近年来,许多数学工作者和化学工作者把研究具有化学背景的特殊图类的拓扑指标作为自己的主要研究方向[3-14]。
本文所研究的图均是无向的连通简单图。设G是具有顶点集V(G)={v1,v2,…,vn}和边集E(G)的一个图,且di表示图G中顶点vi的度。称G中连接度为di的顶点vi和度为dj的顶点vj的一条边为(i,j)-边。用符号eij(G)表示图G中的(i,j)-边的数目。文中没有说明的符号和术语可以参见文献[15]。
Estrada等人于1998年提出的一个图G的拓扑不变量[16],即原子键连通性指标,简称ABC指标且定义如下:
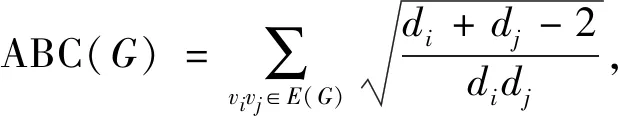
(1)
其中求和符号表示对图G的所有边进行求和.对于ABC指标的应用背景,已被证实其在研究烷烃的热形成中是一个有效的预测性指数,且已被广泛用来研究烷烃的稳定性以及环烷烃的应变能等[5,16].关于ABC指标的研究和众多成果,可以进一步参考文献[17-23]及其所引用的参考文献。
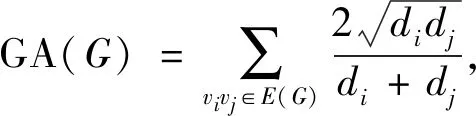
(2)
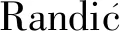
1 基本定义
为了给出本文的研究结果及其证明,首先给出五边形网格螺旋链图的概念。
定义1[29]两个多边形通过一个公共顶点相联,这种联接方式称为螺接;其中公共顶点称为螺接顶点。
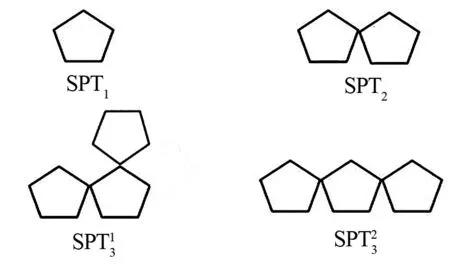
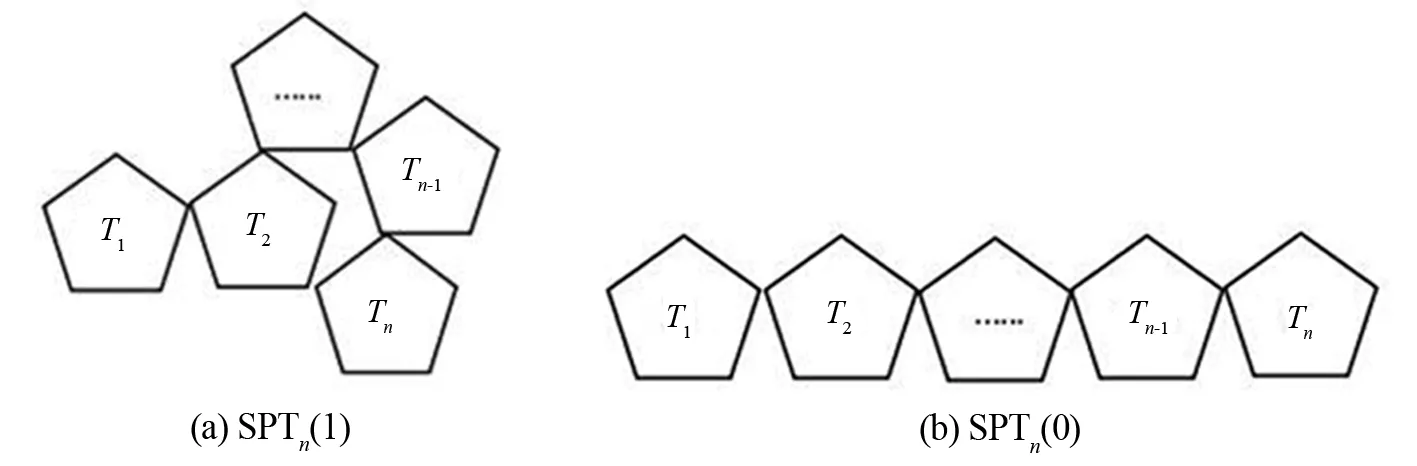
定义2五边形网格螺旋链图是一个由一系列五边形T1,T2,…,Tn构成的1-连通图,而且必须满足:1)对任意的1≤t 不妨用Sn表示具有n个五边形的五边形网格螺旋链图的集合。设SPTn∈Sn,则SPTn(n≥2)可以看作由Sn-1的某一个元素SPTn-1再联接一个五边形而得到,如图1所示。图2显示了n=1,2的唯一五边形网格螺旋链图以及n=3的所有五边形网格螺旋链图;图1显示了五边形网格螺旋链图的一般情形,其中vn-1是SPTn-1中Tn-1的一个顶点。因为每个五边形有5个顶点,所以由图2可知:每个在SPTn-1中的五边形有4个可联接位,即n≥3的SPTn不是唯一的。从图的同构角度考虑,只有两个非同构的螺接方式(图3)。 图1 含有n个五边形的五边形网格螺旋链图Fig.1 The spiro pentagonal chain with n pentagons 图2 n=1,2,3的五边形网格螺旋链图Fig.2 The spiro pentagonal chains with n=1,2,3 图3 五边形网格螺旋链图的两种非同构的螺接方式Fig.3 The two types of non-isomorphic arrangements in a spiro pentagonal chain 本节主要考虑一个随机五边形网格螺旋链图的ABC指标和GA指标的推导和计算。为了方便,沿用在上述部分提到的各个符号和定义的表达含义。如图1所示,设SPTn为通过在五边形网格螺旋链图SPTn-1上联接一个新五边形Tn而得到的一个五边形网格螺旋链图,其中Tn=x1x2x3x4x5。显然,在五边形网格螺旋链图SPTn上只有(2,2)-边、(2,4)-边和(4,4)-边。由此,公式(1)和(2)可以直接改写为: (3) 和 (4) 因此,为了计算五边形网格螺旋链图SPTn的ABC指标和GA指标,只需要确定出SPTn中的不同种类的边数e22(SPTn),e24(SPTn)和e44(SPTn)即可。 定理1设SPTn(p)是一个长度为n的随机五边形网格螺旋链图(n≥2),则 证明当n=2时,SPT2(p)由两个五边形构成且它们之间有一个公共顶点(图2),则容易计算求得 当n≥3时,由图3所示的两种可能非同构联接方式,可以得出e22(SPTn)、e24(SPTn)和e44(SPTn)的具体数量。 和 因此,通过式(3)可以求得: 因此,通过式(3)可以求得: 综上所述,可得出: (5) 由递归式(5)和初始条件可以推导得到: 即定理得证。 利用定理1中完全类似的证明方法,可以计算得到关于GA指标的一个显式表达式。 定理2设SPTn(p)是一个长度为n的随机五边形网格螺旋链图(n≥2),则 定理1和2表明:E[ABC(SPTn(p))]和E[GA(SPTn(p))]关于n都是渐近的且关于p都是线性的。同时,可以利用定理1和2的公式立即得到两类特殊的五边形网格螺旋链图的ABC指标和GA指标的显式表达式,其中两类特殊的五边形网格螺旋链图分别记为SPTn(1)和SPTn(0),如图4所示。 图4 2类特殊的五边形网格螺旋链图Fig.4 The two types of special spiro pentagonal chains 推论1设SPTn(1)和SPTn(0)为如图4所示的两类特殊五边形网格螺旋链图,则 和 推论2设SPTn(1)和SPTn(0)为如图4所示的两类特殊五边形网格螺旋链图,则 和 前文已提到,Sn表示具有n个五边形的五边形网格螺旋链图的集合,则Sn的所有五边形网格螺旋链图的ABC指标和GA指标的平均值可分别定义如下: 和 定理3Sn的每个元素都有ABC指标和GA指标的平均值分别为 和 文献[27]比较研究了有关化学树、分子图和带有一定限制条件的简单图的ABC指标和GA指标的大小。2018年,Wei等又在文献[7]中考虑了随机六边形网格螺旋链图的ABC指标和GA指标的数学期望的大小问题。这里,也将对随机五边形网格螺旋链图的ABC指标和GA指标的数学期望的大小进行比较,并得出相应的结论。 定理4设SPTn(p)是一个长度为n的随机五边形网格螺旋链图(n≥2),则 E[GA(SPTn(p))]>E[ABC(SPTn(p))]。 证明当n=2时,显然有 当n≥3时,由定理1和2可得: 不妨记: 则显然a0>0,a1>0,a2<0,a3<0。因此,当n≥3时,通过计算可以得到: E[GA(SPTn(P)]-E[ABC(SPTn(P)]=[a0p+a1]n+a2p+a3>0, 即 E[GA(SPTn(P)]>E[ABC(SPTn(P)]。 综上所述,可得出:当n≥2时,E[GA(SPTn(P)]>E[ABC(SPTn(P)]。 本文主要研究了随机五边形网格螺旋链图的ABC和GA指标的确定问题。研究了随机五边形网格螺旋链图中的ABC指标和GA指标的数学期望公式;给出了所有含有n个五边形的五边形网格螺旋链图的ABC指标和GA指标的平均值;比较了随机五边形网格螺旋链图中的两个拓扑指标的数学期望,结果表明:随机五边形网格螺旋链图的GA指标的数学期望大于其ABC指标的数学期望。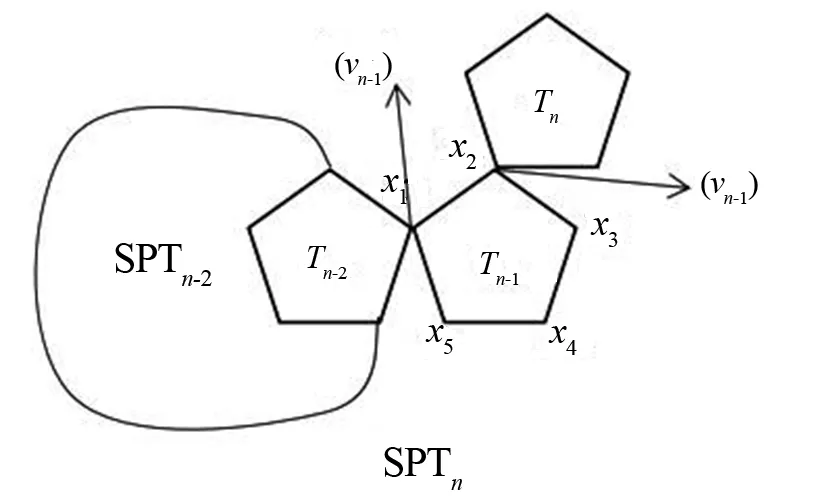
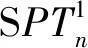
2 随机五边形网格螺旋链图的ABC指标和GA指标


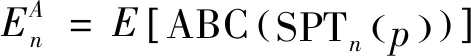
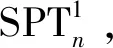
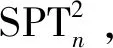
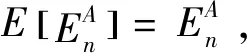

3 五边形网格螺旋链图的ABC指标和GA指标的平均值
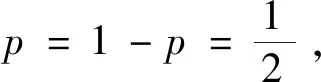
4 随机五边形网格螺旋链图的ABC指标和GA指标的比较
5 结论
