基于Phase数字相机的无人机倾斜摄影测量应用试验

张建霞

(闽江学院海洋学院，福建 福州 350108)

0 引言

我国摄影测量技术已进入数字摄影测量时代。当前随着数码相机技术的飞速发展，其相机的分辨率不断提高，配以当前较为普及的无人机低空摄影平台，使得我国当前的低空摄影测量技术在测绘生产中得到广泛应用与普及，其航测生产的效率得到进一步提升[1]。本文基于单画幅Phase高分辨率数字相机以及无人机航摄平台，研究倾斜摄影测量技术的应用。

1 数字相机的选择

当前用于无人机低空遥感的数字相机大多为索尼、佳能、尼康、宾得等品牌，在倾斜摄影测量技术中，主要使用双拼或五拼等方式进行组合摄影。本研究所选的数字相机为Phase数字相机(图1)，该相机属于较高档的民用工业级数字相机，像素多，分辨率高，具体的技术参数见表1。

图1 Phase数字相机Fig.1 Phase camera

表1 Phase数字相机主要技术参数Fig.1 The chief parameters of Phase digital camera

2 无人机航摄平台

无人机航摄平台的选择主要考虑了有效载荷、续航时间等因素，为了能够搭载较重的工业级Phase数字相机，且具有较长的续航时间，本次航摄采用了CW-20型垂直起降的固定翼油动无人机(图2)，其技术参数见表2。

图2 CW-20型无人机Fig.2 CW-20 UAV

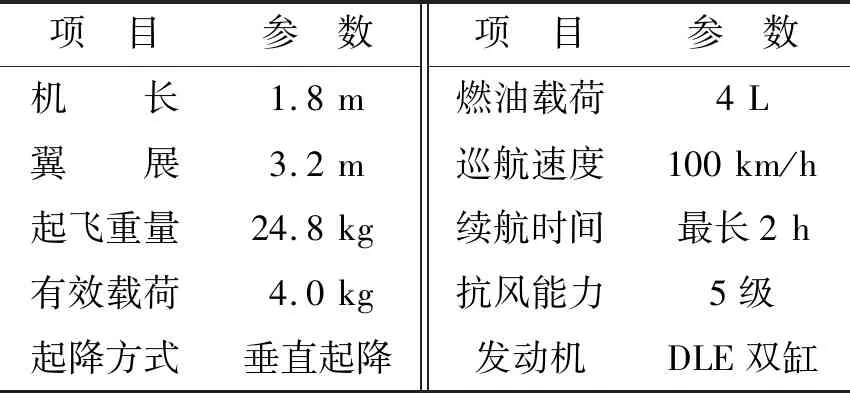
表2 无人机主要技术参数Fig.2 The chief parameters of UAV

3 数码相机几何检校

数码相机为非量测相机，为了消除数码相机的固有误差，须进行几何检校。目前无人机测绘生产中的相机检校大多采用室内检校或屏幕简易检校法，其检校精度较低[2-4]。要实现较高的测绘精度，须采用基于室外检校场的间接摄影测量方法，对应的数学模型如下：

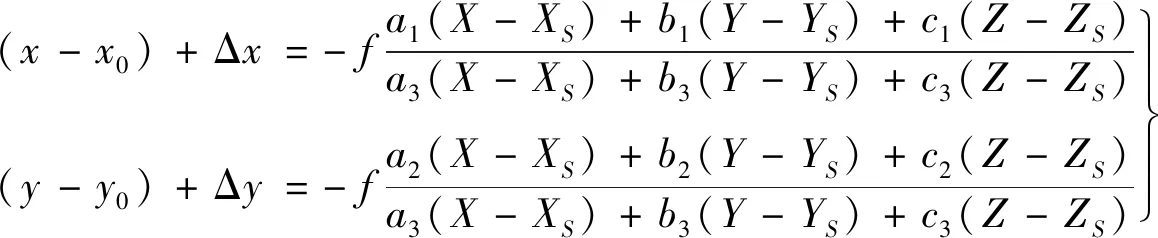
(1)

对式(1)线性化后，得到的平差模型如下(以像点坐标为观测值)：

V=AXE+BXI+CXAD-L

(2)

式(2)中，XE表示影像外方位元素；XI表示影像内方位元素；XAD表示附加参数，主要包括光学畸变改正项[5-7]。

室外检校场设置在某建筑物立面上，在该立面上布设了300个高精度的标志控制点，采用独立坐标系，其精度优于3 mm。通过检校得到的相机主要参数及其精度如表3所示。

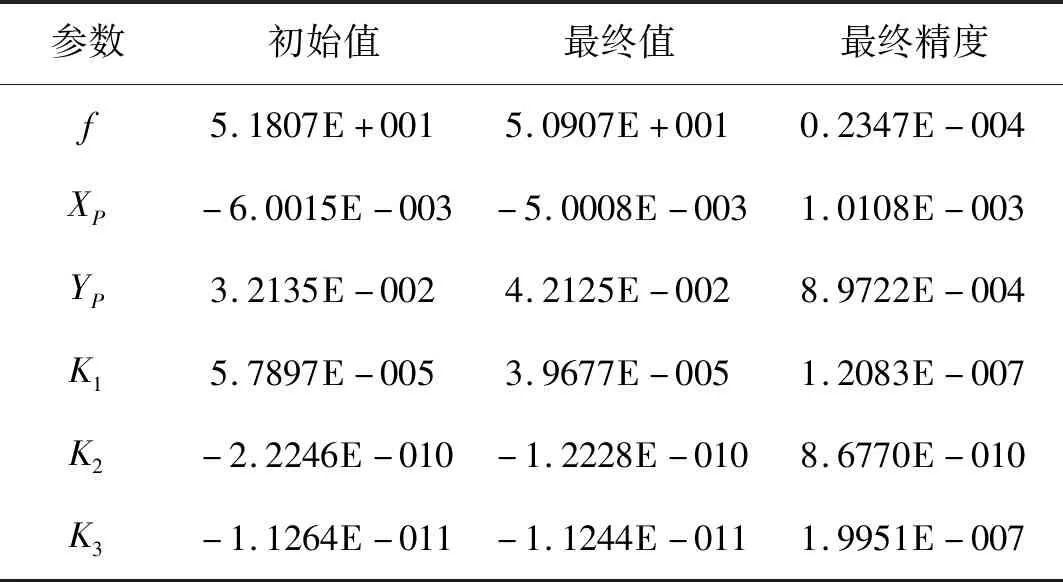
表3 检校主要参数及其精度Tab.3 Calibrated chief parameters and the precision

4 倾斜摄影测量实例

本次倾斜摄影测量的主要工作环节包括航摄设计、航空摄影、地面控制、影像数据摄影测量处理、3D建模、矢量数据采集等[8-9]，具体的技术实现见图3。

图3 倾斜摄影测量技术流程图Fig.3 Technique flow of oblique air survey

4.1 测区航摄设计

测区位于河南省某县，南北长约26 km，东西宽约20 km ，测区包含山地、平原、居民区等，地形较为丰富。航摄设计的GSD为4.0 cm，对应的相对航高为385 m，航线进行正反向井字形飞行设计(模拟45°倾斜四镜头相机的摄影方式)，设计的航向重叠度75%，旁向重叠度60%，设计的部分航线示例如图4。

4.2 航摄影像获取

利用所设计方案进行无人机搭载Phase数字相机的航空摄影，为了减少区域的地面控制工作量，航摄采用了DGPS辅助空中三角测量的方案。本次航摄共飞行1个架次，总航时181 min，获取影像2 958张，影像数据共115 G，获取的航空影像示例见图5。

图4 航线设计图图5 航空影像Fig.4 Designedair-linemapFig.5 Aerialimage

4.3 区域影像空三加密

利用Context Capture软件进行区域影像空三加密，在测区四角布设了4个角控制点，测区中央布设了1个中心控制点，共计5个控制点，并在测区内布设了16个检查点(图6)，其中五角星形点为控制点，近圆形点为检查点。经过带有DGPS的摄站坐标辅助空三加密，其检查点的平面和高程较差统计见表4，因其中有一点为粗差点，所以共统计了15个检查点。由表4的较差统计，算得检查点的平面中误差为±4.4 cm，高程中误差为±5.1 cm。

表4 空三加密检查点误差统计Tab.4 Check-point error statistics of triangulation m

图6 点位分布图图7 区域三维模型Fig.6 PointdistributionmapFig.7 Area3Dmodel

4.4 三维建模与DLG采集

基于上述的空三加密成果，进行区域影像3D实体建模及DLG数据采集，3D实体建模以及基于实体模型的平面DLG采集分别采用的是Smart 3D软件和清华三维的EPS测图软件。经过区域立体三维重建，得到的区域模型示例如图7。经过平面DLG采集，获取测绘的DLG成果，部分示例成果如图8。

图8 基于立体模型的DLGFig.8 DLG based on stereo model

4.5 成果精度

为了验证3D模型及DLG成果的精度，随机选取了12个检查点。在DLG上采集平面坐标，在三维模型上采集高程，经过x，y，h采集，得到的较差统计结果见表5。由表5较差统计，计算得到的平面中误差为±5.5 cm，高程中误差为±7.0 cm。

表5 检查点误差统计Tab.5 Check-point error statistics m

4.6 小结

通过上述的倾斜摄影测量从数据获取到数据处理，再到成果采集及精度验证可知：在航摄GSD为4 cm的情况下，空三加密平面精度为4.4 cm(1.1个GSD)，高程精度为5.1 cm(约1.3个GSD)；区域影像三维实体建模及DLG成果的平面精度为5.5 cm(约1.4个GSD)，高程精度为7.0 cm(约1.8个GSD)。精度满足1∶500的地形图测绘需求，也能够满足1∶1 000的地籍测量需求，并接近1∶500的地籍测量精度[9]。

5 结论与总结

通过本文研究可知：在单幅面Phase数字相机无人机航摄、相机进行高精度几何检校、DGPS辅助空三加密、井字形航线设计、测区四角加中心控制点、GSD为4 cm的情况下，其倾斜摄影测量的成果几何精度介于1～2个GSD，接近1∶500地籍测量的精度需求，对我国当前的无人机航测生产有明显的借鉴意义。

当前的无人机倾斜摄影主要采用的是民用较小像幅的多相机组合航摄，其等效幅面几乎均小于(远小于)工业级Phase数字相机的单机幅面，其多相机拼接为非单中心投影方式，采用的简易屏幕自检校方法精度较低，因此，在倾斜摄影测量应用中，多以牺牲分辨率来获取较高的几何精度，如设计GSD为1～2 cm(航高50～90 m)，其对应的成果精度为5～10 cm，这样，大大降低了航摄效率，并增加了内业处理的工作量和难度。

倾斜摄影测量作为经典摄影测量的新技术手段，可以得到比传统摄影测量更加准确生动的三维实体模型，具有更广阔的应用前景[10-11]。