单孔出流气泡周围流场特性研究

翟建国，鲁天龙，刘庆茶，黄筱云，胡勇虎

(1.中交武汉港湾工程设计研究院有限公司，武汉 430040；2.长沙理工大学 水利工程学院，长沙 410114)

气泡帷幕被广泛应用于各种实际工程中，如异齿裂腹鱼的阻拦[1]、河面破冰工程[2]、异重流防护[3]、水下噪音隔离[4]、水下爆破防护[5]、气幕式防波堤[6]、海上浮油拦截[7]等。在这些实际工程应用中，主要以现场试验用于确定气泡帷幕所需的孔径、空气流量以及孔口间距；但由于气泡本身及其运动引起的流场的复杂性，目前对于气泡帷幕的研究尚不完善，工程应用时对于孔径、空气流量以及孔口间距的确定变得相对困难；为减少实际应用中确定孔径、空气流量以及孔口间距的工作量，对于气泡帷幕的研究是十分必要的。目前国内外学者就气泡帷幕的研究相对较少，但对单个及多个连续气泡运动及其周围流场运动特征进行了大量理论、实验及数值研究。如不可压缩理想流体的气泡输运方程在1917年就被Rayleigh[8]提出，为气泡研究奠定了基础理论；在实验方面主要采用粒子图像测速仪(PIV)对气泡及其运动流场进行测量。如Liu等[9]采用粒子图像测速仪(PIV)对矩形气泡柱中气泡链诱导的流动结构进行了实验研究，得出随着液体粘度的降低，气泡上升轨迹由一维向三维变化，并在实验中观察到自由涡旋，错流和不规则的循环流；Fan等[10]采用粒子图像测速仪(PIV)对不同质量浓度的非牛顿流体中两个平行运动气泡周围的流场进行了实验测量，并对速度矢量、速度等值线和速度分量进行了分析。为了对气泡及其周围流场特性进行更好地分析，学者们对数值模拟也进行了广泛地应用；如徐玲君等[11]对直径为2.6 mm和4 mm的单个气泡进行了数值模拟研究；Bhusare等[12]采用OpenFoam中的欧拉-欧拉双流体模型进行了气液数值模拟，对液体中气泡的速度分布、含气率分布和环流分布情况进行了分析；吴恒等[13]应用VOF方法，分析了不同状态下的气泡脱离时间及直径；Saleh[14]通过使用k-ε闭合湍流模型对三维气液流动进行了模拟，得到小气泡由于没有足够的动量离开壁面，将在壁面跟随液体循环运动。

根据目前的研究，国内外学者对气泡及其周围流场虽然已进行了大量的实验和数值研究，但并未对气泡运动引起的周围流场在断面的分布进行深入地分析。本研究采用OpenFoam中的VOF和标准k-ε模型对单孔出流气泡周围流场特性进行了三维模拟，在此基础上通过改变孔口气体流速、孔口直径进一步对单孔出流气泡周围流场在断面的分布进行深入地分析，为气泡帷幕周围流场运动特性研究打下基础。

1 数值模拟

1.1 控制方程

本研究中，将气体与水体均视为不可压缩相，不可压缩牛顿流体的连续性方程和动量方程如下

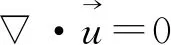
(1)

(2)

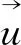
相间边界追踪采用VOF模型，对于第q相，其体积分数方程为

(3)

(4)

式中：α表示体积分数；q表示为第q相。

计算单元中混合流体的密度和粘度的计算方程如下

(5)

(6)

式中：μ表示粘度，Pa·s；g表示气体相。

在连续表面张力(CSF)模型中，气体和水体两相的体积力由式(7)给出

(7)

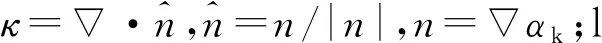
k-epsilon(k-ε)湍流模型是计算流体动力学中最常用的模型，用于模拟湍流条件下的平均流动特性。它是一个双方程模型，通过两个传输方程(PDE)给出湍流的一般描述。对于湍流动能k和耗散率ε由下式定义

(8)

(9)

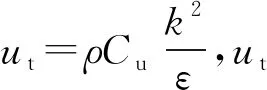
1.2 模型验证

表1 计算流体物理参数

1.2.1 气泡形态验证

根据文献[15]物理实验，选用其孔口气体流速Vg=3.0 m/s，区域尺寸为50 mm×50 mm×100 mm，孔口直径为1 mm的实验条件进行验证。数值计算几何模型及网格绘制如图1所示；计算流体物理参数如表1所示；边界条件设置底部孔口为气体相速度入口边界。数值模拟结果与文献[15]实验结果对比如图2所示，同时给出数值模拟与文献物理实验的初始气泡脱离时间与脱离直径和上升速度对比如表2所示；根据对比结果，可以看出数值模拟得到的气泡运动特性与文献试验结果吻合较好。

图1 几何模型及网格示意图

表2 数值模拟结果与文献[15]实验结果对比表

1.2.2 气泡周围流速验证

选用文献[9]实验中编号S-1下20 ml/min时的实验工况对气泡周围流速进行验证；根据具体的实验工况，数值模拟验证采用底部开孔，孔口直径d为2 mm。通过提取模拟计算得到的点(0，0，33 mm)在x方向速度随时间的变化情况，并与文献此点实验结果进行对比，对比结果如图3所示，由图可见数值计算模拟结果与文献物理实验结果数据趋势基本一致。

1.3 模拟计算工况

本文计算区域几何尺度为1 100 mm×150 mm×250 mm(长×宽×高)，具体几何模型如图4所示，建立直角坐标系，原点(0，0，0)位于底部开孔中心。

图3 数值结果与实测结果比较

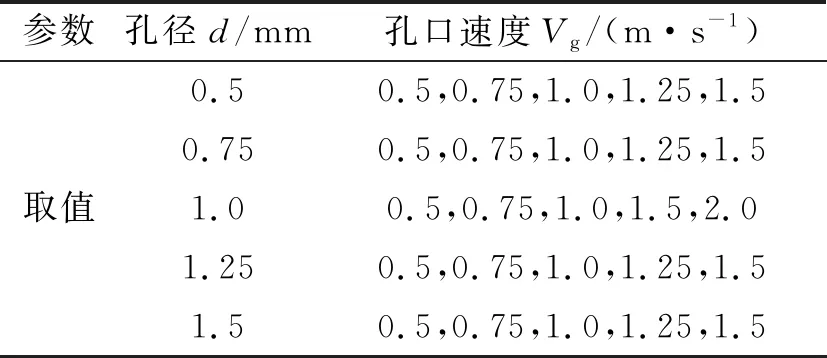
表3 模拟试验参数值

计算模拟水深h=200 mm，孔径及孔口气体流速设计如表3所示。

2 计算结果与分析

2.1 速度等值线图及流线分布

为了清楚地描述不同孔口直径、不同孔口气体流速对周围水体流场的影响，绘制了流线图及不同孔径及孔口气体流速下气泡上升运动过程中的速度等值线分布图。

图5表示孔口气体流速Vg=1.0 m/s，孔口直径d=1.5 mm时x=0断面流线分布情况。由图可见气泡上升运动过程中，气泡首先带动其周围的水体向上运动，在水体到达水面后形成环流扩散开来。

图6表示不同孔口气体流速、孔口直径下x=0断面合速度等值线图，其中图6-a～6-e的孔口直径d均为1.5 mm；图6-f～6-j的孔口气体流速Vg均为1.0 m/s。由图可见气泡上升运动带动的周围流场运动速度主要集中在垂直孔口上方附近两侧；且随着孔口气体流速、孔口直径的增大，连续上升气泡带动的周围水体运动速度相对增大，带动的周围水体运动范围也增大。

2.2 断面垂线平均合速度

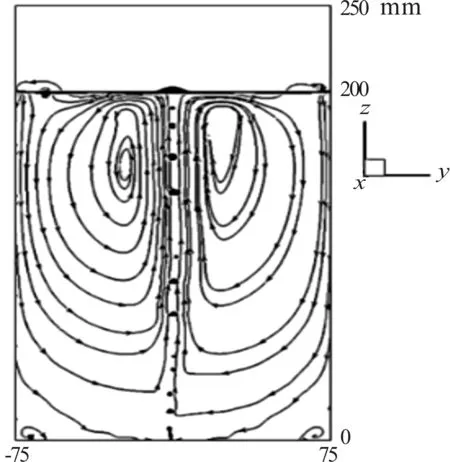
图5 x=0断面流线分布图

为了得到x=0断面垂线平均合速度的分布情况，截取x=0断面，参考方崇等[16]对垂向分布流速的研究，采用三点法对相对水深为0.2、0.6及0.8时的速度进行提取，并进行相应计算。

水深h=0.2 m，孔口气体流速Vg=1.25 m/s时，不同孔口直径下相对水深分别为0.2、0.6及0.8时，合速度在y轴上的分布情况如图7表示；其中图7-a和图7-b分别表示孔口直径d=1.0 mm和d=1.5 mm；图8表示水深h=0.2 m，孔口直径d=1.0 mm，不同孔口气体流速下相对水深分别为0.2、0.6及0.8时，合速度在y轴上的分布情况；其中图8-a、图8-b分别表示孔口气体流速Vg=0.75 m/s和Vg=1.25 m/s；由图7和图8可见，水深h=0.2 m，不同孔口直径、孔口气体流速下相对水深为0.2、0.6及0.8时，合速度在y轴上的分布规律基本相同；同组工况、不同相对水深时，合速度在y轴上的分布差别较小，大体上均呈对称分布，因此可以应用三点法求断面垂线平均合速度。

6-a Vg=0.5 m/s6-b Vg=0.75 m/s6-c Vg=1.0 m/s6-d Vg=1.25 m/s6-e Vg=1.5 m/s

7-a d=1.0 mm7-b d=1.5 mm8-a Vg=0.75 m/s8-b Vg=1.25 m/s

三点法求断面垂线平均合速度的计算公式如式(10)所示，根据提取的相对水深为0.2、0.6及0.8时的速度，可以通过三点法进行计算得到x=0断面垂线平均合速度在y轴上的分布情况。

(10)

式中：Vmag(y)表示y点对应的垂线平均合速度，m/s；Vh(y)表示y点对应的相对水深为0.2、0.6及0.8时的合速度，m/s。

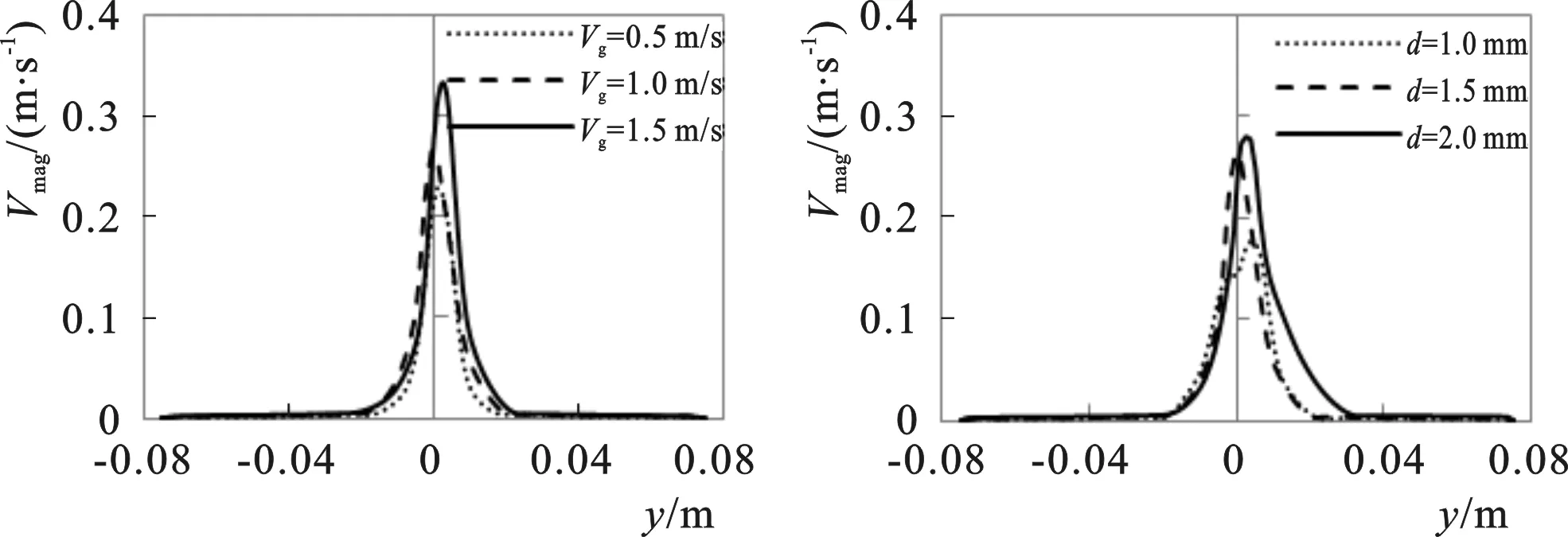
9-a d=1.5 mm 9-b Vg=1.0 m/s

图9-a表示孔口直径d=1.5 mm时，不同孔口气体流速时x=0断面垂线平均合速度在y轴上的分布；图9-b表示孔口气体流速Vg=1.0 m/s时，不同孔口直径时x=0断面垂线平均合速度在y轴上的分布；由图可见，断面垂线平均合速度在y轴上基本呈对称分布；当孔口气体流速、孔口直径较大时，断面垂线平均合速度也相对较大。

2.3 相对速度预测

相对速度D主要受表面张力、粘性力、惯性力的作用，因此可用We、Re等参数对气泡运动引起的周围流场特性进行描述，D、xo、We、Re数的计算公式为

(11)

(12)

(13)

(14)

式中：Vmag表示垂线平均合速度，m/s；Vg为孔口出气速度，m/s；xo表示相对孔径；y表示y轴坐标值，m；d为孔口直径，m；ρl为液体的密度，kg/m3；ρg为气体的密度，kg/m3；σ为表面张力系数，N/m；μl为液体黏度，kg/(s2·m)。

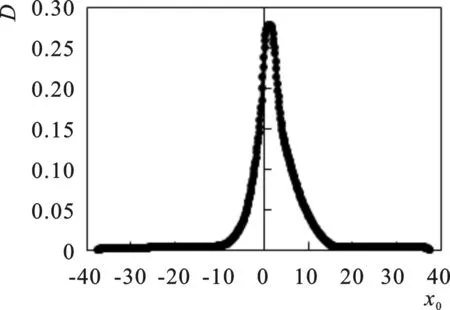
图10 D与xo的关系图

根据图9-b中孔口直径d=2.0 mm，孔口气体速度Vg=1.0 m/s时x=0断面垂线平均合速度的数据，应用式(11)和式(12)进行计算处理得到D与xo，其关系曲线如图10所示；结合分布曲线对D与xo的关系曲线进行直接高斯分布概率密度函数拟合，其相对速度分布预测公式如式(15)所示。

(15)

式中：yo、A、σ和μ为待定系数；由式(15)可知，在给定孔口气体速度Vg和孔口直径d的条件下，为了得到相对速度D的分布情况，需要对上式中含有的yo、A、σ和μ四个未知参数进行预测，考虑到对称性及水深h的影响，取μ=0；因此，采用h/d、We和Re数对上述未知参数进行拟合。

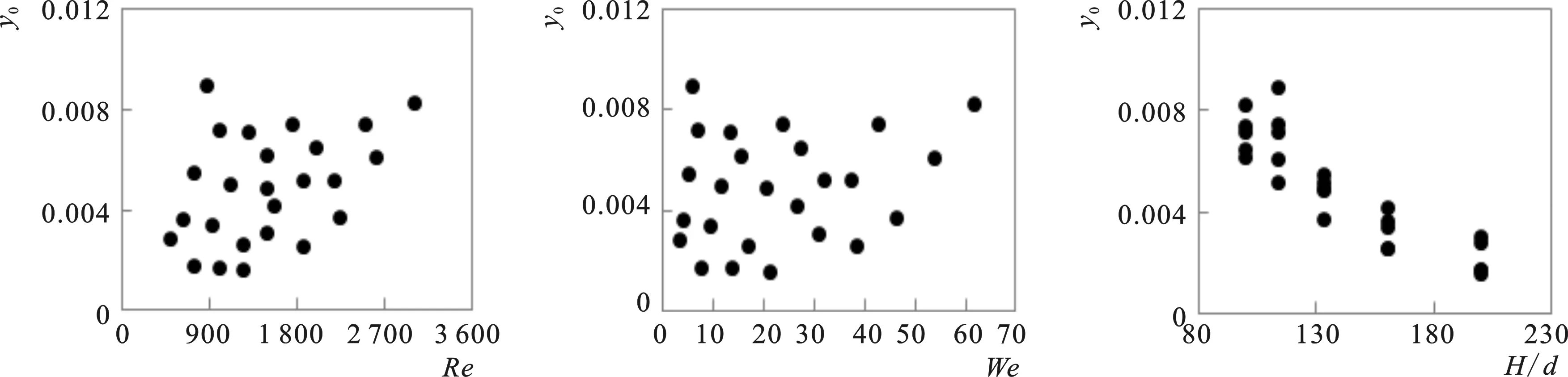
11-a yo～Re11-b yo～We11-c yo～H/d

图11表示yo与Re、We和H/d的关系图，其中图11-a表示yo与Re数的关系图，图11-b表示yo与We数的关系图。由图11-a、图11-b可见yo与Re和We数的关系不明显，故不使用Re和We数对yo进行预测；由图11-c可以看出yo总体随H/d增大而减小。

从图11可以看出：yo与H/d几乎呈线性相关，因此可构建σ与H/d之间的关联式，通过对计算数据进行拟合，找出yo的最佳预测模型

(16)

式中：ao、bo为待定系数；通过一元非线性方法对式(16)进行计算数据拟合，得到其待定系数ao=0.011 9、bo=-5.09×10-5以及均方误差S=0.002 827、平方绝对误差Sr=9.138 4×10-7和相关系数r=0.891 1。

A与Re、We和H/d的关系如图12所示。由图12-a、图12-b可见A整体随Re数及We数的增大而减少；由图12-c可以看出A与H/d关系不明显，因此不使用H/d对A进行预测。

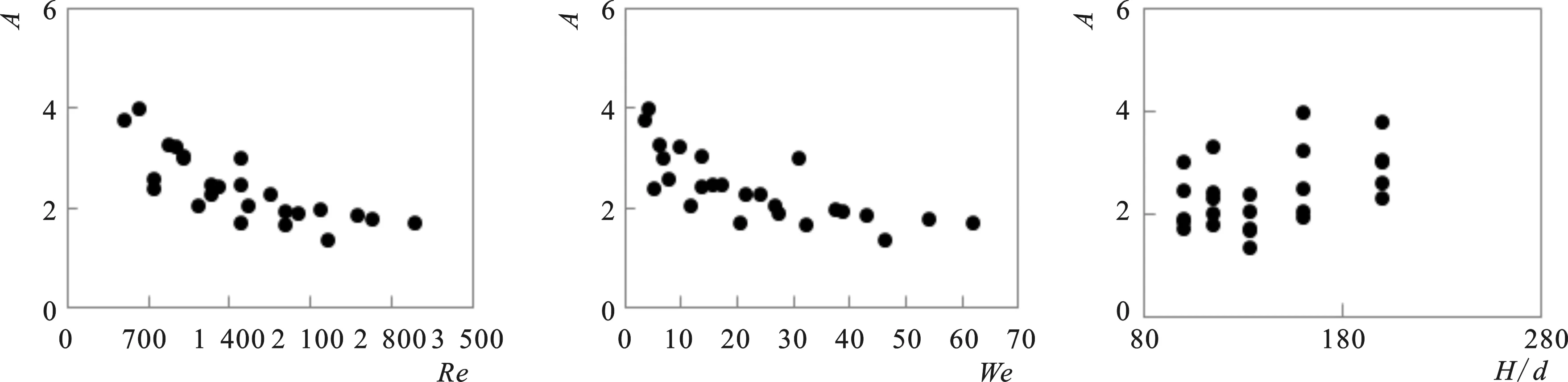
12-a A～Re12-b A～We12-c A～H/d

从图12-a、图12-b可以看出：A随着We数和Re数的增大呈现减小的趋势，因此可构建A与We数和Re数之间的幂函数关联式对数据进行拟合

(17)

式中：a1、b1、c1、f1为待定系数；Qi分别取We数和Re数，通过对上式应用一元非线性方法对模拟数据进行拟合，计算得到其待定系数a1、b1、c1、f1以及相关参数如表4所示。

表4 相关参数

图13表示σ与Re数、We数及H/d的关系图，由图13-a、图13-b可见σ与Re和We数的关系不明显，图中数据点较分散，因此不采用Re数和We数对σ进行预测；由图13-c可以看出σ随H/d的增大而增大。

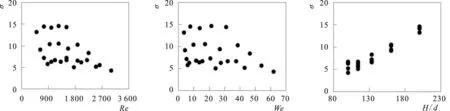
13-a σ～Re13-b σ～We13-c σ～H/d

图13表示σ与Re数、We数及H/d的关系图，由图13-a、图13-b可见σ与Re和We数的关系不明显，图中数据点较分散，因此不采用Re数和We数对σ进行预测；由图13-c可以看出σ随H/d的增大而增大。

(18)

式中：a2、b2为待定系数；通过一元非线性方法对上式进行计算数据拟合，得到其待定系数a2=-5.14、b2=0.096 5以及均方误差S=2.181、平方绝对误差Sr=0.790 5和相关系数r=0.961 4。

综合式(16)～式(18)及表4，可以得到yo、σ与A最佳预测模型，具体拟合公式如下

(19)

(20)

(21)

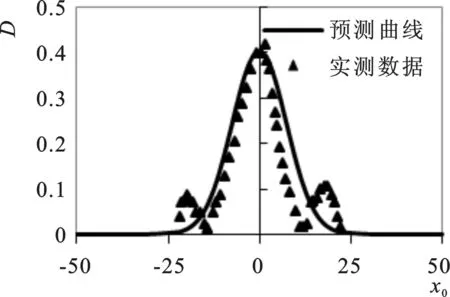
图14 实测数据与预测曲线D与xo关系图

为了验证以上公式的合理性，选用文献[9]中实验编号为S-4下Q=20 mL/min，孔口直径d=2 mm工况下的实验数据对上式进行验证；首先根据实验条件通过式(19)～式(21)计算得到相对速度D与xo的预测曲线；再根据实验数据得到的直线上速度分布的数据，根据式(11)、(12)计算得到D与xo，并一同绘制于图14；由图14可以看出实测数据基本分布在预测曲线周围，所以此模型是可以用于断面垂线平均合速度的预测。

3 结论

本文应用OpenFoam软件对单孔出流气泡进行了三维模拟，通过改变孔口气体流速、孔口直径对气泡运动引起的周围流场特性进行了分析研究，得到以下结论：(1)连续上升气泡会带动周围的水体在上升气泡两侧形成环流；(2)随着孔口气体流速、孔口直径的增加，气泡运动引起的周围流场速度逐渐增大，影响范围也逐渐增大；(3)断面垂线平均合速度随孔口气体流速、孔口直径的增大而增大；(4)拟合出基于高斯分布函数的相对速度预测公式，且与实验数据吻合较好。