测试人牙周膜粘弹性力学特性的纳米压痕实验条件研究

施昊天，鹿如鑫，刘 鑫，刘 懋，黄辉祥，吴 斌，严 斌

牙周膜(periodontal ligament,PDL)是牙齿和牙槽骨之间的重要连接组织，在正畸力作用下其介导牙槽骨的改建，影响牙齿的移动[1]。研究牙周膜的力学行为是正确理解正畸生物力学机制以及合理预测正畸治疗结果的关键。牙周膜为一种厚度为0.15～0.38mm的结缔组织[2]，主要由纤维、细胞和基质组成，其中基质中含有70%左右的水。以往研究表明牙周膜是一种典型的非线性材料[3]，多样的成分组成导致其力学特性非常复杂，兼具弹性和粘性。力学实验是精确了解牙周膜组织力学特性的最佳方法，传统的反应力学特性的实验包括拉伸、压缩、剪切等，但体内实验在现有的条件下难以开展[4]，已有的实验研究中大部分是宏观的拉伸实验[5-6]。而牙周膜结构的复杂性以及受样本制备与仪器功能的限制，导致宏观实验获得的牙周膜组织力学特性参数并不够精确。

纳米压痕是一种在微小区域内测试力学性能的有效实验方法，近年来被广泛应用于软骨、角膜等生物材料[7]，具有精度高、对样品形状要求低、操作简便等优点[8]。对于粘弹性材料，为在微观层面测试其力学性能，需开展的纳米压痕实验通常包括基于纳米压痕的蠕变实验[9]和基于纳米压痕的约化弹性模量测试[10]，前者主要通过纳米压痕时间-位移曲线的保载段变化研究材料的粘性特征，而后者主要通过载荷-位移曲线的卸载段变化研究材料的硬度和约化弹性模量等弹性属性。

Ashrafi等[11]使用Berkovich压头将牙周膜视为一种普通的韧带进行实验获得了时间和蠕变柔度关系的曲线，但样本量仅为一颗人牙。傅肄芃等[8]通过Oliver-Pharr法[12]得到并比较了犬牙根不同层面的牙周膜的约化弹性模量；Huang和Wu等[13-14]使用猪和犬的牙周膜组织开展了纳米压痕实验，并通过有限元法模拟了实验过程，从而验证了粘弹性模型的适用性。但上述研究存在以下缺陷，包括：①动物牙周膜样本不能完全反映人牙周膜特性；②部分压头，如Berkovich压头的选择不适用于软组织实验[15]；③未强调保湿条件，可能影响结果的稳定性[16]；④蠕变实验中未强调加载率的控制以尽可能达到阶跃载荷[17]；⑤基于纳米压痕的约化弹性模量测试中未严谨控制参数条件消除蠕变效应[10]；⑥载荷的选择过小，导致应力应变曲线不完整。

因此，为了获得更准确的人牙周膜纳米压痕实验数据，需要对纳米压痕实验条件和参数进行控制。本研究应用人牙周膜样本，使用0.2mm直径的平头压头，在对保湿条件进行稳定控制的条件下，分别研究基于纳米压痕的蠕变实验和约化弹性模量测试的合适参数范围，包括加载率、保载时间和峰值载荷等，以期获得更合理的测试人牙周膜粘弹性力学特性的纳米压痕实验方案，为明确人牙周膜力学特性提供参考。

1 材料与方法

1.1 主要实验材料与仪器

健康人类上颌骨3个[24～52岁，南京医科大学伦审(2019)324号]。

纳米压痕仪(Nano Indenter G200，Agilent，美国)，压头为可替换的金刚石圆柱形平头压头(半径为100μm)，见图1A；低速切割机(IsoMet, Buehler, 美国, 500r/s)，见图1B；自制保湿容器(专利申请号：CN109520837A)；切片石蜡(上海华灵康复机械厂，熔点 56～58 ℃)；迷你钢锯(SATA，304.8mm)；图表制作软件Origin(Version 9，origin-lab，美国)。

A：纳米压痕仪,B：低速切割机

图1主要实验仪器图

Fig.1Experimental instruments

1.2 实验方法

1.2.1 样本制作与处理 样本制备当日从-20 ℃冰箱中取出人上颌骨，如图2A，去除软腭、牙龈等软组织。使用骨锯切取人上颌切牙样本9个，在石蜡包埋下用低速切割机切为垂直于根长轴的(2.0±0.3)mm的厚切片，如图2B。每例样本牙取根中段，如图2C，共获取9个包含牙周膜的人切牙根中段样本。切割好的样本置于生理盐水中并保存在-20 ℃环境下[18]。实验当天，从冷冻室中取出样本于室温下解冻，测试室的温度保持在环境温度25 ℃。

A：人上颌骨样本；B：低速切割机切割后的人前牙样本；C：不同牙根位置的样本

图2样本预备示意图

Fig.2Preparation of samples

1.2.2 基于纳米压痕的蠕变实验 ①加载率的确定：将解冻后的来自不同上颌骨的3个牙周膜根中段样本(样本1、2、3)置于保湿容器中并固定于纳米压痕仪器加载台上，自制保湿容器见图3。在样本周围滴注生理盐水后，于100倍光镜下选取牙周膜宽度>0.2mm的实验位点并开始纳米压痕实验，分别选取(0.1 mN/s、0.3 mN/s、0.5 mN/s、0.7 mN/s)的加载率加载至3 mN后直接卸载，每个点均使用平头压头反复进行压痕，每次压痕间隔15min以待牙周膜充分恢复，每个参数重复3次实验以验证可重复性。②蠕变实验：将所得数据作载荷-位移曲线，选取合适的加载率参数，进行保载200 s的蠕变实验。

图3 保湿装置与根中部样本

1.2.3 基于纳米压痕的约化弹性模量测试 ①保载时间的确定。在基于纳米压痕的约化弹性模量测试中需使用Oliver-Pharr法[12]求约化弹性模量，在使用Oliver-Pharr法时，应避免蠕变效应的影响，为使蠕变效应饱和从而消除其影响，需在峰值载荷下维持足够的保载时间[19]。Xia等[20]根据保载段曲线模型拟合所得时间参数得到进入缓慢钝化阶段的时间节点，以确定保载时间。使用该定量方法时需使用粘弹性模型，本研究选取Burgers模型，此模型是研究粘弹性材料性状最常用的模型之一[20-21]，以往研究中，Burgers模型与不同材料的纳米压痕实验数据拟合较好[22]，且可以得出纳米压痕过程中不同材料粘弹性行为的精确变化。使用该模型拟合压痕曲线保载段的公式如下[23]：h=he+h1(1-e-t/τ)+t/μ。其中，h是压痕位移，t为保载时间，he是加载阶段后的弹性形变。τ为保载达到稳定阶段所需的缓冲时间，h1为初始段粘弹性系数，μ为保载段曲线进入稳定阶段后的线性变化斜率的倒数[9]。②确定基于纳米压痕的约化弹性模量测试的保载时间范围。选取另3个不同人牙周膜样本(样本4、5、6)，在相同加载率和载荷下，分别使用(25、50、75 s)的保载时间进行实验，压痕方法同1.2.2，作载荷-位移曲线。对曲线卸载段使用Oliver-Pharr法计算约化弹性模量，以分析保载时间对约化弹性模量计算的影响，计算得到的约化弹性模量越大，保载时间对其的影响越小；使用保载时间定量法，拟合保载段曲线以得到时间参数，并加入10 s缓冲时间以避免误差[20]。③确定基于纳米压痕的约化弹性模量测试的载荷范围。取其余3个不同人牙周膜样本(样本7、8、9)，在相同加载率和保载时间下，使用(1 mN、2 mN、3 mN、4 mN)峰值载荷进行纳米压痕实验，压痕方法同1.2.2，作载荷-位移曲线及蠕变速率曲线。识别不具有完整性的载荷-位移曲线，以排除过小的载荷范围。计算比较不同载荷下的约化弹性模量和蠕变速率，分析适合基于纳米压痕的约化弹性模量测试的载荷范围。

2 结 果

2.1 基于纳米压痕的蠕变实验

在使用0.1、0.3、0.5、0.7 mN/s 4种加载率进行纳米压痕实验时，每种加载率参数重复3次实验的载荷-位移曲线趋势近似相同，具有可重复性。为便于观察消除误差，将每个参数所得载荷及位移数据取平均后作图(图4)。图像显示，随着加载率减小，加载段的峰值载荷和最大压痕位移增大。为分析比较加载率对压痕曲线稳定性的影响，取每次实验加载段达到的最大载荷作加载率-最大载荷趋势图(图5)，发现0.3～0.5mN/s的加载率既能达到2.9～3.0mN的峰值载荷，也有相对较短的加载时间，为较适合人牙周膜基于纳米压痕的蠕变实验的加载率参数范围，而选取0.5mN/s加载率可达到更接近阶跃载荷的效果。

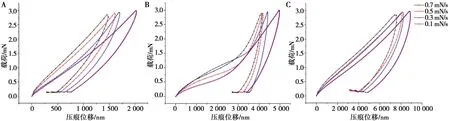
A：样本1;B：样本2;C：样本3

图4载荷-位移关系图

Fig.4Load-displacement diagram

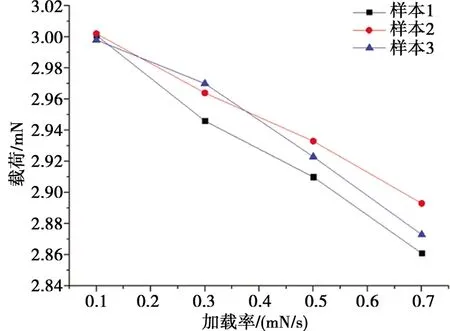
图5 加载率-最大载荷趋势图

选取0.5mN/s加载率进行保载200s的蠕变实验，时间-位移曲线如图6所示，表明了人牙周膜具有蠕变行为。

图6 纳米压痕蠕变曲线

2.2 基于纳米压痕的约化弹性模量测试

2.2.1 保载时间范围 分别使用25、50、75 s的保载时间进行基于纳米压痕的约化弹性模量测试，对卸载段使用Oliver-Pharr法进行约化弹性模量计算，发现约化弹性模量随保载时间增长呈递减趋势(见图7)，因此应尽量选取较短的保载时间以避免其对约化弹性模量计算的不利影响。

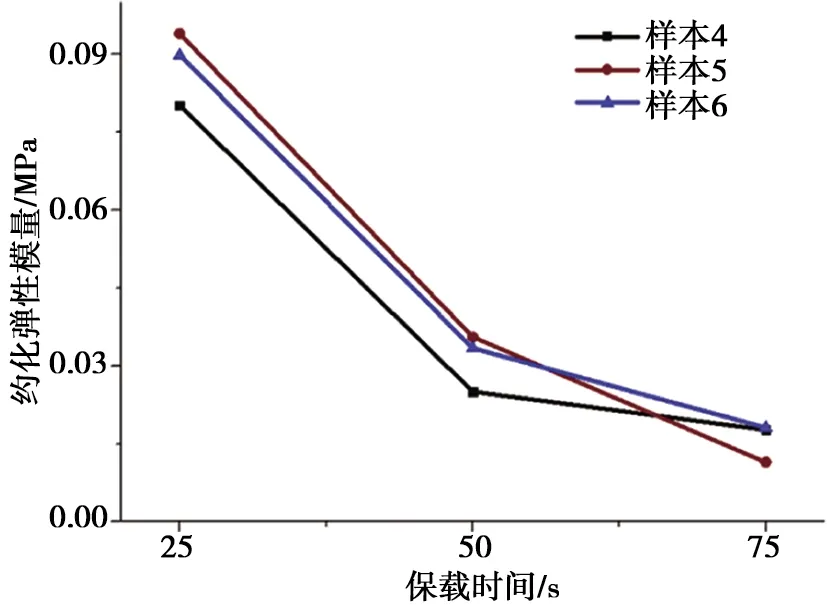
图7 约化弹性模量变化随保载时间变化趋势图

使用Burgers模型对曲线保载段进行拟合(见图8)，比较3组样本拟合所得的时间参数τ，分别为15.6、14.9、15.7s。即0.5mN/s加载率下牙周膜蠕变曲线在保载开始后约15s达到缓慢钝化阶段，此时进行压痕卸载，即可基本避免蠕变效应的影响。同时为避免误差，参考Xia等[20]的方法在15s的基础上增加10s的缓冲时间，以优化实验结果。最终，选取25s作为基于纳米压痕的约化弹性模量测试的保载时间参数。

图8 75s保载段曲线拟合Burgers模型

2.2.2 峰值载荷范围 分别使用1、2、3、4mN的峰值载荷进行基于纳米压痕的约化弹性模量测试结果如图9所示，载荷为1mN时，曲线不完整。图10A、B分别为不同载荷下的保载段时间-位移曲线和时间-蠕变速率曲线，在1～3mN的峰值载荷下，蠕变曲线更早达到稳态。蠕变速率在保载初始迅速下降，随后趋于平缓，当载荷小于3mN时，蠕变速率在保载时间达到20s后几乎已降至稳定，但载荷4mN以上的蠕变速率在保载20s时仍然较大。为避免过大的蠕变效应，峰值载荷选取不宜大于4 mN。

图9 载荷-位移曲线图

A：保载段时间-位移曲线；B： 保载段时间-蠕变速率关系

图10保载时间-蠕变速率关系图

Fig.10Curve of relationship between loading timeand creep rate

使用Oliver-Pharr法求取2～4mN载荷实验的约化弹性模量范围为0.012～6.840 MPa，如图11所示，其值随峰值载荷的增加而降低。4mN时载荷对于弹性模量计算值的影响较大。提示2～3mN为较合理的实验参数范围。

3 讨 论

蠕变为粘弹性的主要表现形式，蠕变实验可反映粘弹性材料在受力状态下的稳定性和长期负载能力[24]。Ashrafi等[11]使用人牙周膜得到了时间-蠕变柔度曲线，但并未给出具有蠕变行为的时间-位移曲线。本实验观察到，人牙周膜在保载200s的过程中出现了长期非弹性形变逐渐增加的蠕变行为，证明了人牙周膜不仅有弹性特征，还有粘弹性材料特有的时间依赖性特性。

纳米压痕蠕变实验加载段为斜坡载荷，而理想的拉伸蠕变为施加阶跃载荷。本研究中，0.1mN/s的加载率过慢，压痕位移较大，即在加载过程中会产生额外的粘弹性形变[25]。0.7mN/s的加载率与预设载荷偏离较远，根据Yang等[17]研究，过快的加载率会导致预设压痕载荷出现较大的超调，易引起峰值载荷的失稳。因此，为了减轻粘弹性形变的影响，选择0.3～0.5mN/s的加载率可在保持较快加载率的同时尽量保证实验结果的稳定性。

以往基于纳米压痕测试牙周膜的约化弹性模量时并未对保载时间进行控制与分析。本实验结果显示(见图5)，蠕变速率最初随着保载时间的推移迅速降低到接近稳定状态，在15s后进入缓慢钝化阶段。可能是随着保载时间的延长，纤维间的相对运动越来越剧烈，使得粘性得到充分表达，引起蠕变速率的迅速变缓。这也印证了在消除蠕变效应的同时不宜选取过长的保载时间。本研究中选取25s的保载时间测试弹性模量取得了较好的效果，未发现蠕变效应的不利影响。

以往对人牙周膜的纳米压痕实验常使用小于等于1mN的载荷[8]，本实验发现，此时加载段曲线未完全展开，牙周膜纤维性质未充分表达，难以算得精确的弹性模量。但载荷设定过大也存在不利影响。本实验中，随峰值载荷增大，约化弹性模量降低，考虑为蠕变效应增大可能导致牙周膜纤维的软化[26]。同时，由于压痕深度增大，接触面积增加[27]，导致牙周膜纤维的自恢复更显著地发生在压头周围的区域中。此外，更深的压痕深度会使牙周膜表层纤维和基底的关系发生变化。虽然牙周膜样本厚度足够，但由于其并非各向同性的整体，而是多层牙周膜纤维的堆叠，同样可能存在基底效应[28]。因此，在牙周膜纳米压痕设定载荷时，还需要考虑到对压痕深度和峰值载荷进行限定，防止约化弹性模量计算精度的下降。本实验结果表明，2～3mN是测试约化弹性模量时较合适的载荷范围。

在以往的研究中，最常被使用的压头为Berkovich压头，此类压头尖端锋利，由弹性到塑性行为的转变几乎瞬间发生，更适用于刚性材料的实验[15]。而本研究使用平头压头具有以下优势：①在压痕过程中，接触面积保持不变，因此接触压力随压痕载荷的线性增大而增大，便于约化弹性模量的计算；②压痕中心周围的堆积或下沉对压痕应力没有影响，体现为蠕变曲线的稳定；③载荷与位移曲线可显示一个清晰的屈服点，可以更容易更准确地与材料性能相关联。同时，使用大半径的平头用于软组织的纳米压痕测试可使其工作范围更大。牙周膜的宽度为0.15～0.38mm，因此,选用0.2mm直径的平头压头，既能适应牙周膜的宽度，又能减少表面粗糙度对实验结果的不利影响。

Yamashita等[29]的研究表明，温度对胶原纤维的粘弹性没有产生显著影响，而组织的含水量对其粘弹性有显著影响。本实验使用保湿装置增加了数据的稳定性和可重复性，减少了机械反应改变的风险；然而，即使样品已经保温保湿，实验环境仍然无法模拟真正的生理状态。未来可发展更先进便捷的表面处理技术和体内测试技术以提供更接近真实的实验数据。

4 结 论

本文对人牙周膜纳米压痕实验的实验条件和优化参数范围进行了初步研究，得出了以下结论：①本研究通过基于纳米压痕的蠕变实验验证了人牙周膜的粘弹性性质，通过基于纳米压痕的约化弹性模量测试得到了人牙周膜的约化弹性模量为0.012～6.840 MPa；②人牙周膜基于纳米压痕的蠕变实验建议使用0.3～0.5 mN/s的加载率；③人牙周膜基于纳米压痕的约化弹性模量测试建议使用25 s的保载时间和2～3 mN的峰值载荷以消除蠕变效应的影响。本研究获得了合理的测试人牙周膜粘弹性力学特性的纳米压痕实验方案，为明确人牙周膜力学特性提供了参考。