牙科氧化锆陶瓷压痕尺寸效应模型评价*

王培娜 潘 祁 李 秦 金英哲 刘振霞

全瓷修复体因其良好的生物相容性、理想的美学效果被广大修复患者所接受。氧化锆（Yttria partially stabilized zirconia，Y-TZP）陶瓷是应用最多的全瓷类修复材料，相比其它陶瓷材料，它拥有硬度高、热导率低、绝缘、耐磨、色泽稳定等优点［1-4］。目前，为了最大程度保留患者自体牙体组织，同时实现患者对美观和舒适的双重要求，口腔临床医生越来越青睐制作薄氧化锆Y-TZP陶瓷修复体。然而，在咬合力集中区域，薄氧化锆Y-TZP陶瓷修复体经常出现局部变形破坏。硬度作为体现Y-TZP陶瓷抵抗局部变形破坏的一个非常重要的力学性能，是口腔医生进行修复体局部厚度优化设计的基础。

通常说，Y-TZP陶瓷的硬度值为常数，并且硬度值越高，局部越不易变形破坏［5-7］。然而，目前国外文献研究表明Y-TZP陶瓷硬度存在压痕尺寸效应，即沿厚度方向压痕实验确定的硬度值随压痕深度变化而变化。Mei和Renjo等研究表明Y-TZP陶瓷硬度随着沿厚度方向压痕深度的增大而减小最后趋于定值［8，9］，即正压痕尺寸效应；Wang等实验结果表明沿厚度方向硬度随压痕尺寸增大先增大后减小最终趋于定值，即先逆后正压痕尺寸效应［10］。由于国内文献关于Y-TZP陶瓷压痕尺寸效应的研究较少，只有王培娜等开展了不同氧化锆陶瓷压痕尺寸效应分析及其真实硬度确定方法的研究[11]，这导致国内口腔临床医生进行Y-TZP陶瓷修复体厚度优化设计时忽略硬度的尺寸效应［12，13］。此外，现阶段开展冷热循环、着色液、酸碱腐蚀等劣化因素对Y-TZP陶瓷硬度影响研究时，忽视Y-TZP陶瓷劣化从表面到内部逐渐变化，认为压痕实验测得硬度值是常数，导致已有方法难以反映Y-TZP陶瓷厚度方向梯度劣化特征［5，14-16］。

为了准确描述沿厚度方向压痕实验确定的硬度值随压痕深度变化规律，研究者采用各种模型去描述Y-TZP或其它种类陶瓷压痕尺寸效应［8-10，17，18］。然而，一方面，目前国内外研究只是采用众多压痕尺寸效应模型中的一种或几种去描述Y-TZP陶瓷正压痕尺寸效应，对已有模型能否同时描述Y-TZP陶瓷正和逆压痕尺寸效应还未开展研究；另一方面，由于压痕尺寸效应的存在，确定Y-TZP真实硬度需要进行大量试探性压痕实验，需要耗费大量时间和金钱［19-21］。因此，本文通过收集和文献[11]相同的五种Y-TZP陶瓷压痕尺寸效应实验数据，这是现有文献能查阅到的所有Y-TZP陶瓷压痕尺寸效应实验数据，并回顾现有压痕尺寸效应模型，然后对现有压痕尺寸效应模型进行分析评价，阐明每种压痕尺寸效应模型的优缺点，推荐能准确描述Y-TZP陶瓷压痕尺寸效应的模型；在此基础上，阐明了逆压痕尺寸效应产生原因，为修复体厚度优化设计提供指导［22-26］。

1.材料和方法

1.1 Y-TZP陶瓷压痕尺寸效应实验材料 现有大量关于各种材料压痕尺寸效应研究［27-29］，由于本文只关注Y-TZP陶瓷压痕尺寸效应，因此通过查阅作者能获取的国内外涉及Y-TZP陶瓷压痕尺寸效应实验所有文献资料，本文只收集到数字光处理（Digital light processing，DLP) (QuickDemos，中国)、机械加工（Milled，MILL) (Zenostar，列支敦士登)、电泳淀积（Electrophoretic deposition，EPD) (Tosoh，日本)、添加A3染料（A3是一种牙科染料）和无染料（NA3表示在没有进行染色) (Newport Beach，美国）五种Y-TZP陶瓷压痕尺寸效应实验［8-10，30］。五种Y-TZP陶瓷晶粒尺寸如表1所示，其中A3和NA3 Y-TZP陶瓷晶粒尺寸相同，且所有Y-TZP陶瓷晶粒大小都在纳米尺度。DLP、MILL、A3和NA3 四种Y-TZP陶瓷化学组成主要为ZrO2+HfO2占比约95%、Y2O3占比约5%和Al2O3占比小于1%，EPD Y-TZP陶瓷化学组成原文献没有给出。

表1 五种Y-TZP陶瓷晶粒尺寸（nm)

1.2 Y-TZP陶瓷压痕尺寸效应实验方法［11］

按照标准（ASTM C1327-2015)，DLP、MIL 采用硬度计（Zuanshi，中国）测试维氏硬度，A3 和NA3 采用硬度计（Wilson-Wolpert，美国）测试维氏硬度，压头面夹角为138°，EPD Y-TZP 材料采用纳米玻氏压头压痕仪（NHT2，奥地利)［31］，压头面夹角为121.6°。常温下，施加不同大小载荷压入陶瓷表面，保持一定时间后卸除载荷，材料表面便留下一个压痕，测量压痕对角线的长度d，其中维氏硬度可以由如下公式求得：

纳米硬度由如下公式计算：

上式中，Pmax表示最大载荷，a和b为压头的形状参数，分别为a=0.1891、b=24.56，d为压痕对角线长平均值（d=(d1+d2)/2)，hc为压痕深度。在进行硬度测试时，载荷范围要大，以便能全面体现Y-TZ压痕尺寸效应，并且为了减小实验误差，保证结果的准确性，每种载荷需要停留10-15s，A3和NA3 Y-TZP陶瓷每种载荷硬度测试30次，MILL和DLP Y-TZP陶瓷每种载荷硬度测试10次，EPD Y-TZP陶瓷进行了59次不同压痕深度测试。为了统一，采用公式（3)(q为压头面角）计算DLP、MILL、A3和NA3 四种Y-TZP陶瓷压痕深度hc。

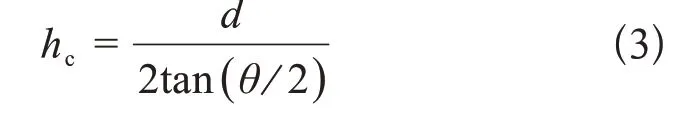
1.3 Y-TZP压痕尺寸效应实验数据收集 为了对比发现不同Y-TZP材料的压痕尺寸效应规律，并在此基础上定量评价下文公式（4)-(10）七种已有压痕尺寸效应模型，本研究收集文献［8-10］中五种Y-TZP压痕尺寸效应实验数据［11］。

1.4 压痕尺寸效应模型回顾 为了统一，采用公式（1）和（3）把所有P-d形式模型转化为公式（4)-(10）所示的H-hc形式。下面公式（4)-(10）中aij(i=1-7，j=1-3)、m、n和r为和压头形状、材料特性、弹性恢复、塑性变形和位错密度等因素相关的材料参数，下面不再逐一说明。

Meyer模型［32］

Hays-Kendal模型［33］

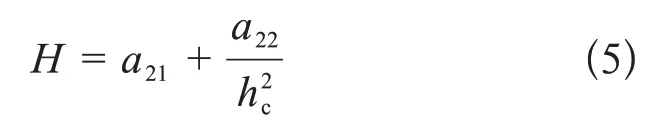
Li-Bradt93模型［34］

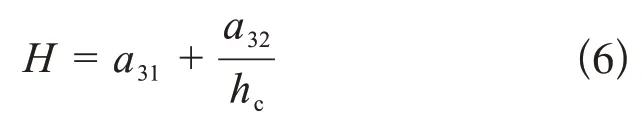
Bull模型［35］

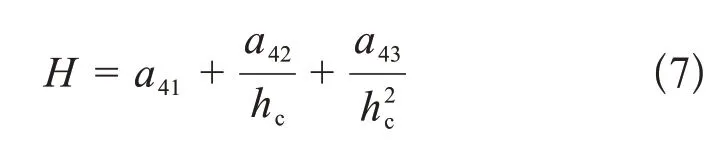
Li-Bradt96模型［36］，采用Meyer模型的P-d关系式P=Adn把Lih-Bradtrc 模型转化为如下H-hc形式：

Nix-Gao模型［37］

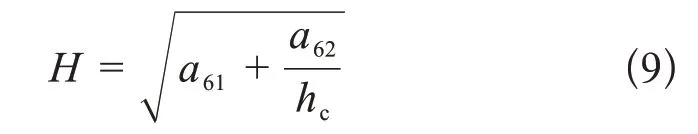
修正Nix-Gao模型［38］

1.5 压痕尺寸效应模型参数确定方法 首先取DLP Y-TZP材料压痕尺寸效应实验数据，然后采用公式（4）的Meyer模型拟合DLP实验数据确定Meyer模型对应DLP数据的参数a11和m，最后分别取MILL、A3、NA3和EPD四种Y-TZP材料压痕尺寸效应实验数据，用Meyer模型依次拟合确定这四种Y-TZP材料实验数据对应的模型参数a11和m。对于其余公式（5)-(10）六种压痕尺寸效应模型，采用上述相同方法确定其材料参数。

1.6 压痕尺寸效应模型定量评价 为了定量评价尺寸效应模型预测结果的准确性，首先把1.5节确定的模型参数代入对应模型，然后把实验数据中的压痕深度hc依次代入模型得到硬度预测值Hp，最后把预测Hp和对应试验硬度值He代入下面公式计算相关系数R2［9，18］：

上式中，k 表示每组拟合数据数量，同时计算五种Y-TZP陶瓷相关系数R2总和的平均值，即总平均相关系数（T-R2)，并采用确定的R2和T-R2定量评价不同压痕尺寸效应模型预测实验数据的准确性。

2.结果

2.1 五种Y-TZP压痕尺寸效应实验数据［11］下面表2-4给出了DLP、MILL、A3、NA3和EPD五种Y-TZP陶瓷材料压痕实验数据。由表2和3可以看出，随着压痕深度hc增大，DLP、MILL、A3和NA3 四种Y-TZP陶瓷硬度减小并逐渐趋于固定值，即正压痕尺寸效应［8，9］。由表4可以看出，EPD Y-TZP陶瓷的硬度随hc增大先增大后减小然后逐渐趋于固定值，即先逆后正压痕尺寸效应［10］。此外，DLP、MILL、A3、NA3四种Y-TZP压痕尺寸效应实验数据差异具有统计学意义（P＜0. 05)，EPD Y-TZP原文中给出了所有的实验数据，从下文图1(e）可以看出数据差异较小，具有统计学意义。

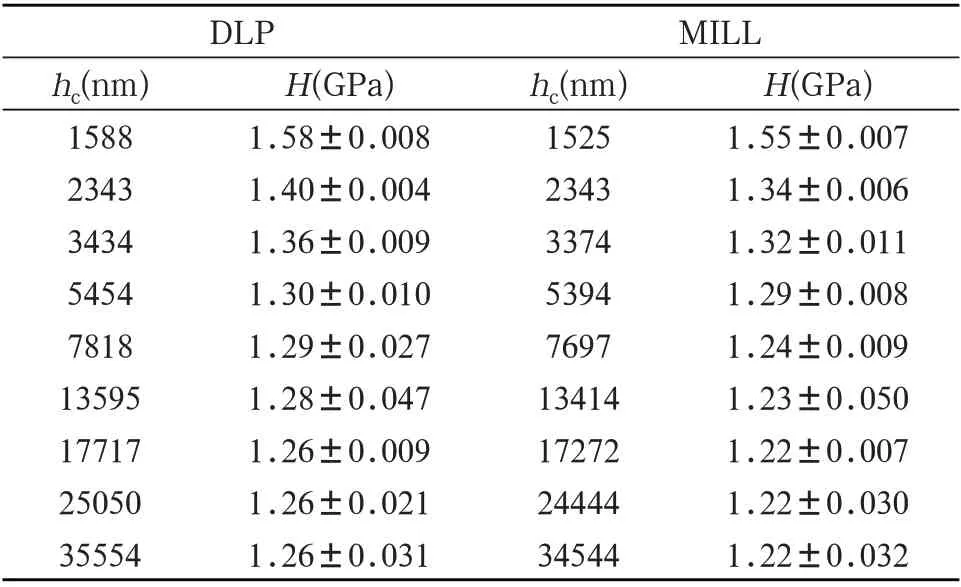
表2 DLP和MILL Y-TZP压痕尺寸效应实验结果［8］

表4 EPD Y-TZP压痕尺寸效应实验结果［10］

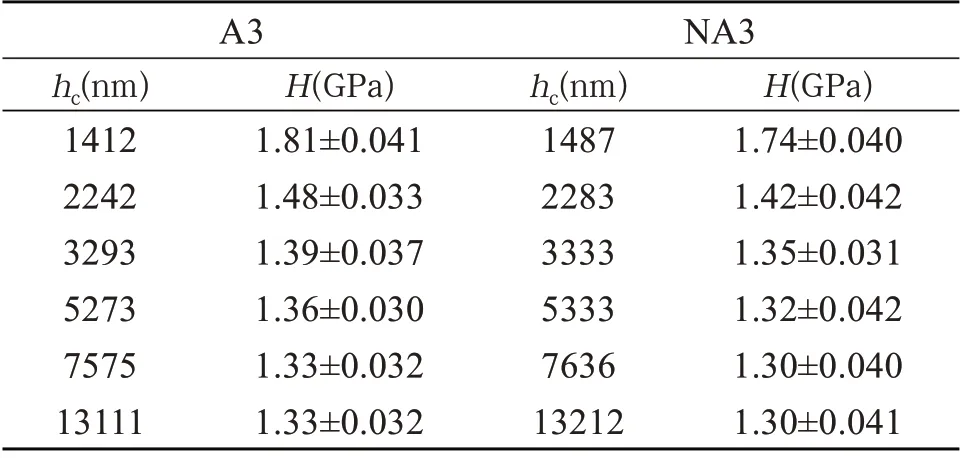
表3 A3和NA3 Y-TZP压痕尺寸效应实验结果［9］

2.2 压痕尺寸效应模型参数值DLP、MILL、A3、NA3 和EPD 五种Y-TZP 压痕实验数据对应的公式（4)-(10）七种压痕尺寸效应模型参数如下表5 所示。可以看出，除Bull 和Li-Bradt96 模型，由DLP、MILL、A3、NA3 和EPD 五种Y-TZP 陶瓷压痕实验数据确定的其余模型参数正负不变。

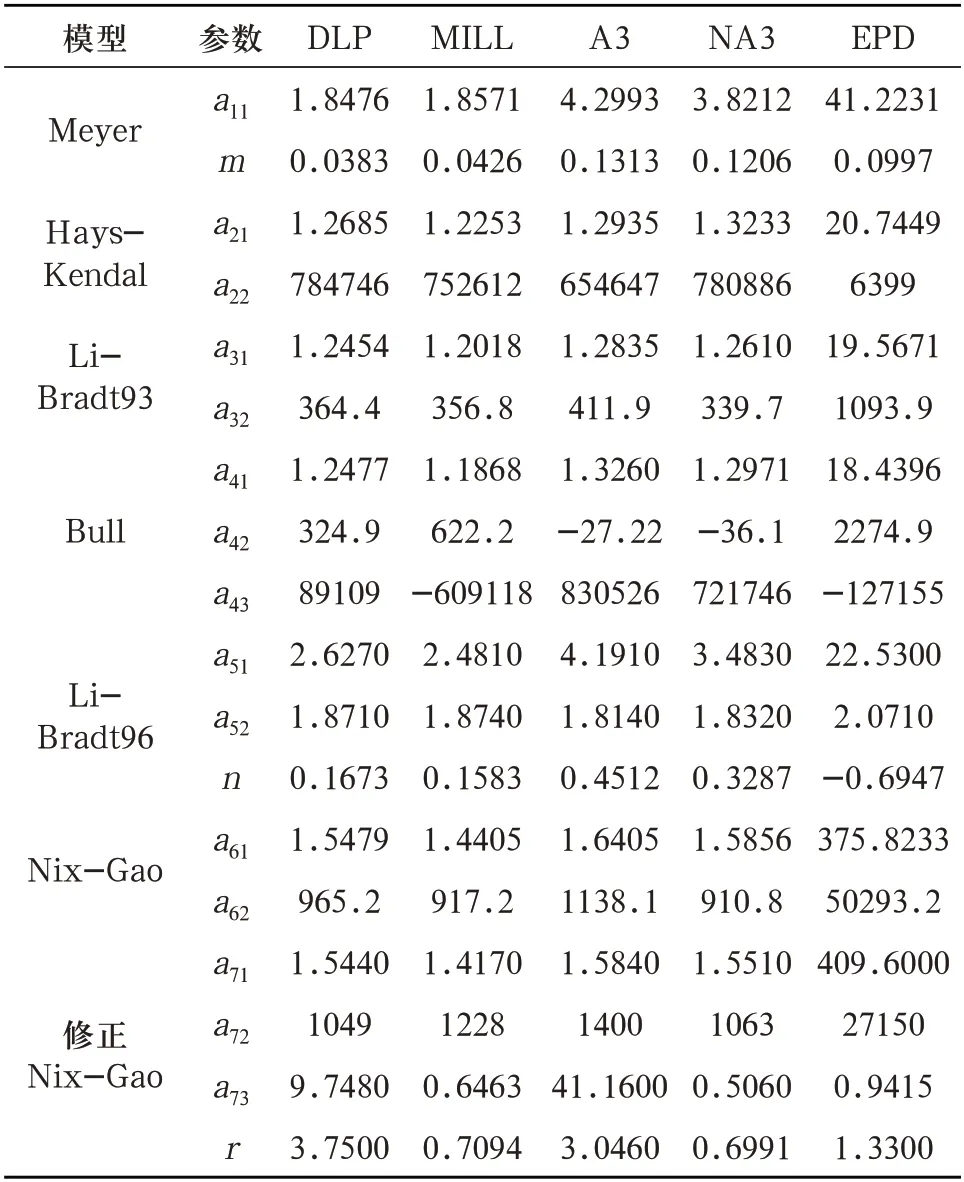
表5 压痕尺寸效应模型拟合参数

2.3 压痕尺寸效应模型定量评价结果 表6给出公式（4)-(10）七种模型和实验数据定量对比的相关系数R2和总平均相关系数T-R2。从表6可以看出，Bull 模型总平均相关系数T-R2最大为0.8984，Hays-Kendal模型次之为0.7847，接下来依次为修正Nix-Gao模型0.7486、Nix-Gao模型为0.7481，Li-Bradt93模型为0.7476，Li-Bradt96为0.7059，最后为Meyer模型为0.63484。而描述DLP、MILL、A3和NA3 四种Y-TZP陶瓷正压痕尺寸效应时，Bull、Hays-Kendal、 修 正 Nix-Gao、 Nix-Gao、Li-Bradt93、Li-Bradt96和Meyer模型的总平均相关系数T-R2分别为0.9885、0.9805、0.9136、0.9086、0.9198、0.7808和0.7169。只有Bull和Li-Bradt96模型能预测EPD Y-TZP陶瓷先逆后正压痕尺寸效应，但是相关系数R2很小，分别只有为0.5380 和0.4064。本研究中，当把五种Y-TZP实验数据和七种模型全部在图中表示时，由于不同模型的曲线之间重叠，图形示例过于接近，难以分辨，因此对于DLP、MILL、A3和NA3四种Y-TZP陶瓷，在定性对比的图1(a)-(d）中只画出表6中总平均相关系数T-R2较大的三个模型（Bull、Hays-Kendal和修正Nix-Gao模型)，同时在图1(a)-(d）中把这三个模型的重叠部分进行局部放大处理。对于EPD Y-TZP陶瓷，在图1(e）中只画出能描述先逆后正压痕尺寸效应的Bull和Li-Bradt96模型。

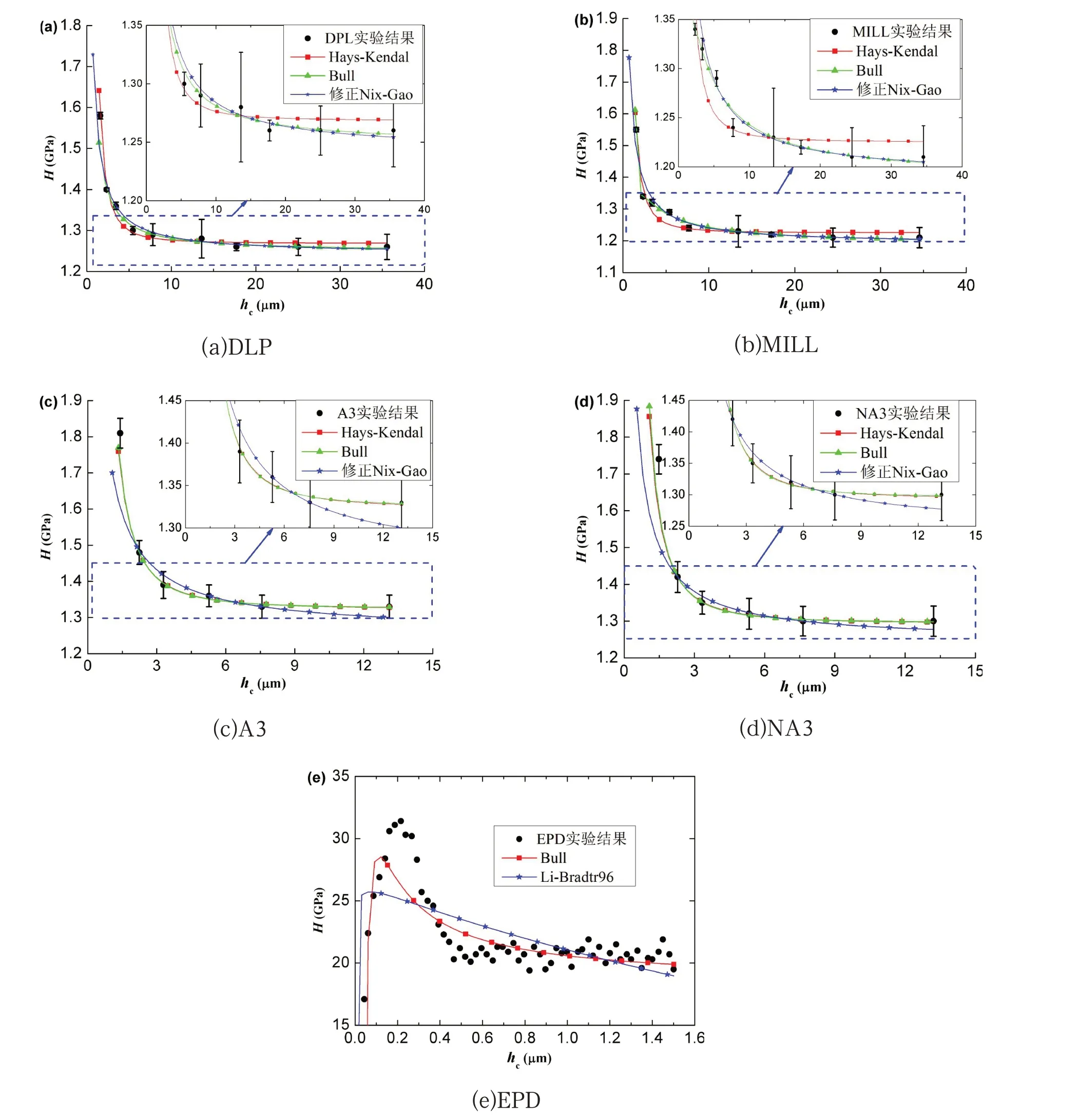
图1 五种Y-TZP陶瓷压痕尺寸效应实验和模型预测对比

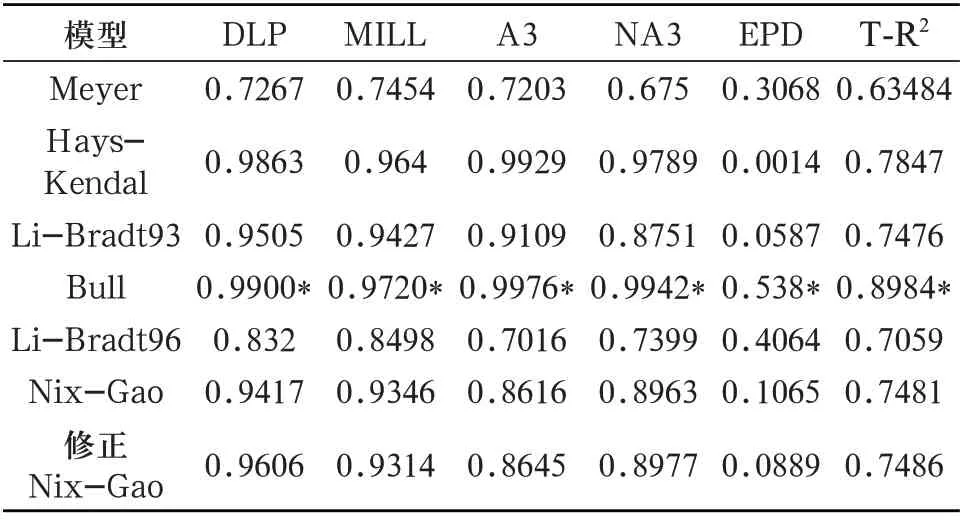
表6 压痕尺寸效应模型预测相关系数R2

3.讨论

从图1(a)-(d）可以看出，随着压痕深度hc增大，DLP、MILL、A3和NA3 四种Y-TZP陶瓷硬度减小并逐渐趋于固定值，即正压痕尺寸效应。可以看出公式（4)-(10)7种尺寸效应模型都可以描述正压痕尺寸效应，然而，Meyer模型不能描述压痕深度趋于无穷大时，硬度趋于固定值这一现象，Hays-Kendal、Li-Bradt93、Bull、Nix-Gao和修正Nix-Gao可以描述正压痕尺寸效应中硬度随hc增大逐渐减小并逐渐趋于固定值。对于正压痕尺寸效应发生机理，Bull和Hays-Kendal模型认为塑性滑移［10］，修正Nix-Gao和Nix-Gao 模型假设为应变梯度导致几何必须位错［37］。事实上，随着压痕深度增加，塑性滑移区逐渐增大，几何必须位错数量逐渐增多，而几何必须位错是产生塑性变形的根源［37，39］，这意味上述两种正压痕尺寸效应解释都可归结为塑性区随压痕深度的非线性变化，这也是上述四种模型能同时正确描述正压痕尺寸效应的原因。因此，结合表6和图1(a)-(d)，本文推荐描述Y-TZP陶瓷正压痕尺寸效应宜采用总平均相关系数T-R2最大的三参数Bull模型（R2=0.9885）或次之的两参数Hays-Kendal模型（R2=0.9805)。

由图1(e）可以看出，EPD Y-TZP陶瓷的硬度随hc增大先增大后减小然后逐渐趋于固定值，即先逆后正压痕尺寸效应［10］。在上述7种尺寸效应模型中，只有Bull和Li-Bradt96模型能预测EPD Y-TZP陶瓷先逆后正压痕尺寸效应，这也是表5 中Bull 和Li-Bradt96模型材料参数正负发生变化的原因。对于逆压痕尺寸效应发生机理，只有Li-Bradt96模型认为试件加载过程中的压痕开裂是产生逆压痕尺寸效应的原因［36］，而其它六种模型都不具有描述逆压痕尺寸效应的机理。但是由表6 和图1(e）可以看出，Li-Bradt96模型预测先逆后正压痕尺寸效应相关系数R2=0.4064非常小，这就意味着现有压痕尺寸效应模型都不能准确的描述EPD Y-TZP陶瓷先逆后正压痕尺寸效应。

事实上，由图1可以看出DLP、MILL、A3和NA3四种Y-TZP 材料实验观察到正压痕尺寸效应，而EPD Y-TZP材料实验观察到先逆后正压痕尺寸效应。由表2-4可以看出，五种Y-TZP材料实验压痕深度范围DLP为1588 nm≤hc≤35554 nm、MILL为1525 nm≤hc≤34544 nm、A3 为1412 nm≤hc≤13111 nm、NA3为1487 nm≤hc≤13212 nm、EPD为43 nm≤hc≤1500 nm。由表1给出DLP、MILL、A3、NA3 和EPD 晶 粒 大 小dg分 别 为：603 nm、591 nm、425 nm、425 nm 和175 nm。而DLP、MILL、A3、NA3和EPD实验最小压痕深度hcm为分别为：1588 nm＞dg=603 nm、1525 nm＞dg=591 nm、1412 nm＞dg=425 nm、1487 nm＞dg=425 nm 和43 nm＜dg=175 nm。对比五种Y-TZP材料晶粒大小dg和最小压痕深度可以看出：实验数据只观察到正压痕尺寸效应的DLP、MILL、A3和NA3 四种Y-TZP材料实验最小压痕深度远大于其晶粒大小dg，而同时观察到先逆后正压痕尺寸效应的EPD Y-TZP材料，最小压痕深度hcm=43 nm 远小于晶粒大小dg=175 nm，这意味实验最小压痕深度远小于晶粒大小是产生逆压痕尺寸效应原因，这和Yang等在纳米铜压痕尺寸效应实验中观察到的结果一致［29］。

综上所述，本文在收集牙科Y-TZP陶瓷压痕尺寸效应实验数据和回顾现有压痕尺寸效应模型基础上，通过对实验数据和模型进行对比分析和评价，本研究推荐采用Bull 模型或Hays-Kendal 模型描述Y-TZP陶瓷正压痕尺寸效应，但是目前尚没有模型能准确描述Y-TZP陶瓷先逆后正压痕尺寸效应，实验最小压痕深度远小于晶粒大小是产生逆压痕尺寸效应原因。