高速列车构架载荷解耦降维标定方法及试验验证
2022-06-26李俊杰任尊松吴养民王玉伟
李俊杰,任尊松,吴养民,王玉伟
(1.北京交通大学机械与电子控制工程学院,北京,100044;2.中车青岛四方车辆研究所有限公司,山东青岛,266031)
转向架构架是高速列车的关键部件,承受并传递来自轮轨和车体的各种载荷,其结构可靠性对列车运营安全至关重要。构架结构强度设计和疲劳试验均需准确的载荷数据,因此,构架载荷标定试验及其数据处理的方法显得尤为重要。
动态载荷识别是结构动力学的反问题[1-2]。而反向求解常遇到病态矩阵问题,使载荷识别不准确或者精度降低。病态矩阵求解通常有奇异值法[3-4]、Tikhonov法[5]和共轭梯度法[6]。近年来,又提出了小波分析法、神经网络法、遗传算法等[7-9]。郭爱民等[10]针对飞行器难建模、难约束和难收敛问题,将其受力简化为平面应变状态,计算单位密封条压缩力,然后在舱门铰链处定义转动副并约束转动角位移,同时在密封位置施加与单位长度密封压缩力等效的压强,得到铰链支反力矩,实现了载荷解耦。韩玉旺等[11]针对直升机桨叶受挥舞、摆振和扭转3种复合载荷作用,提出了一种基于应变片桥路组合的方法,消除挥舞对摆振的影响,得到更为真实的载荷数据。陈道云等[12]针对构架强耦合载荷,采用样条空间插值法分别获得了3种工况下的强耦合区域内部的应变分布,将2 种干扰载荷工况应变等高线交叉为0 的点选为齿轮箱载荷识别测点,获得真实的线路载荷。段垚奇等[13]针对载荷与应变之间耦合问题,在处理标定数据时提出一种多元回归选元法,选出最优自变量参数组合,得到较佳的回归结果。
转向架结构载复杂,列车实际运行时,构架受多种载荷同时作用,各种载荷系耦合严重,增加了载荷识别难度。本文作者提出一种解耦降维标定方法,对某高速列车构架载荷标定,消除各载荷之间的耦合影响,减小载荷识别误差,保证构架载荷实测精度,为构架的后续载荷谱编制、耐久性试验和寿命分析提供数据支撑。
1 载荷标定方法
1.1 载荷系划分
依据构架结构型式和运动模式,结合文献[14-15],可将作用在构架上的载荷划分为浮沉载荷F1、侧滚载荷F2、扭转载荷F3、横向载荷F4、牵引载荷F5、齿轮箱垂同向载荷F6、齿轮箱垂反向载荷F7、电机垂同向载荷F8、电机垂反向载荷F9、电机横向载荷F10、菱形载荷F11、抗蛇行载荷F12、抗侧滚扭杆载荷F13、制动载荷F14和二系垂向减振器载荷F15这15种载荷,其作用位置和方向如图1 所示。构架载荷系多达15 种,各载荷系之间必定存在耦合关系。

图1 构架载荷系示意图Fig.1 Schematic diagram of frame load system
1.2 解耦降维标定试验方法
对于大型结构的载荷标定处理,通常采用直接回归标定和反向回归标定[16-17]。本标定实验是以载荷输入作为控制变量,逐级加载,各载荷识别点的应变响应为输出,反向回归法可以更好地描述本次实验过程,因此,本文选择反向回归法,其载荷应变模型为

反求载荷时,式(1)可以写成:

由于转向架构架载荷系众多,导致矩阵K求解困难,并且K易产生奇异,使结果准确性和可靠性较差。为解决上述问题,采用解耦和降维的方法来求解矩阵K。
解耦是使各载荷加载工况理想,即各载荷系完全独立互不影响,每一个载荷识别点的响应值是对应加载载荷的唯一响应[18-19]。由于各载荷测点只受各自对应载荷的影响,可将载荷-应变传递系数矩阵K非对角元素化为0,变为对角矩阵,实现载荷和应变的一一对应关系,即可简化为

通过在构架上单独施加等梯度的载荷,得到该载荷对应的载荷识别点响应值,进而确定载荷-应变传递系数。
若某一载荷识别点由多种载荷信号混叠,不能完全解耦时,可对矩阵进行降维处理。将无影响或者影响较小的载荷剔除,使载荷的维数尽可能减小,使矩阵K变为稀疏矩阵。
在构架载荷标定过程中,将标定试验分为2种:一种是各类减振器和抗侧滚扭杆等简单构件,由于其结构受力简单,只受拉压或扭转,可根据式(3)对其进行单独标定,载荷识别精度高且不受其他载荷影响。另一种是在构架上布置的载荷识别点,如浮沉、电机载荷等,构架结构复杂,力源较多,需要考虑载荷之间的耦合关系。解耦降维标定方法主要包含以下4个步骤:
1)对构架单独施加各个载荷系,通过有限元法计算并分析各个载荷系下的应力分布情况。
2)确定各载荷系下的强响应区和弱响应区。
3)在各载荷系对应的强响应区,同时是其他载荷系对应的弱响应区进行布片。
4)对构架进行单独加载,验证载荷解耦降维效果。
为了评定解耦和降维方法的有效性和准确性,定义耦合度来描述某一载荷识别点在除该识别载荷外,其余加载载荷下对该载荷识别点的影响,耦合度γij计算公式为
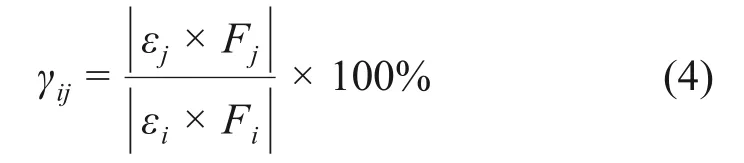
式中:γij为第j种载荷对第i个载荷识别点的耦合度;εi和εj分别为在第i种和第j种单独载荷加载下的应变响应值;Fi和Fj分别为第i种和第j种载荷理论值,根据EN13749标准获得。
1.3 加载标定
通过有限元计算确定了构架上各个载荷识别点的布片位置,按照载荷系示意图(图1)对构架进行加载,获得各载荷识别点的响应值。考虑到列车实际运营工况是多种载荷共同作用,且存在载荷系的不同组合,除了进行单独加载外,还设计了由2种载荷组成的组合加载进行对比。同时,通过3种载荷组合加载(工况11)得到的应变响应值和传递系数矩阵来反推加载载荷进行验证,加载工况见表1。

表1 构架加载工况Table 1 Loading conditions of framework
为减少周围环境的干扰,标定试验环境选为无加速度、振动、冲击、恒温的实验室。将构架正置于专用的疲劳试验台,安装轮轴及转臂,用4个特制工装代替轮对,对构架垂向进行约束。通过千斤顶和力传感器调整构架整体平衡,使构架各轴端分担的力一致。为了减少构架和加载设备之间间隙的影响,施加1 kN或3 kN预载。为了消除机械滞后影响,试验中重复加载3次。
2 载荷标定数据分析
2.1 单独加载下载荷-应变分析
单独加载下的载荷应变模型为式(3),以浮沉载荷F1和电机垂反向载荷F9为例,3次单独加载这2 个载荷的F-ε分布如图2 所示。从图2可以看出:两者均呈现较好的线性相关性。采用最小二乘法进行线性拟合,取3次拟合结果的均值作为载荷应变系数。浮沉载荷的传递系数k1,1为11.0;电机垂反向载荷的传递系数k9,9为11.3。

图2 单独加载下载荷-应变分布Fig.2 Load-strain distribution
根据式(4)对各载荷测点的耦合度进行分析。浮沉载荷识别点和电机垂反向载荷识别点的耦合度分别见表2和表3。

表3 电机垂反向载荷识别点耦合度Table 3 Coupling factor of F9 load identification point
从表2可以看出,齿轮箱垂同向载荷F6、电机垂同向载荷F8、制动载荷F14和二系减振器载荷F15对浮沉载荷识别点的耦合度远远超过误差允许范围,即这4种载荷对浮沉载荷识别点的影响不能忽略,其余载荷对浮沉载荷识别点的耦合度均在5%以内,在误差允许范围内,可以认为这些载荷已解耦。文献[20]对浮沉载荷、侧滚载荷的定义为
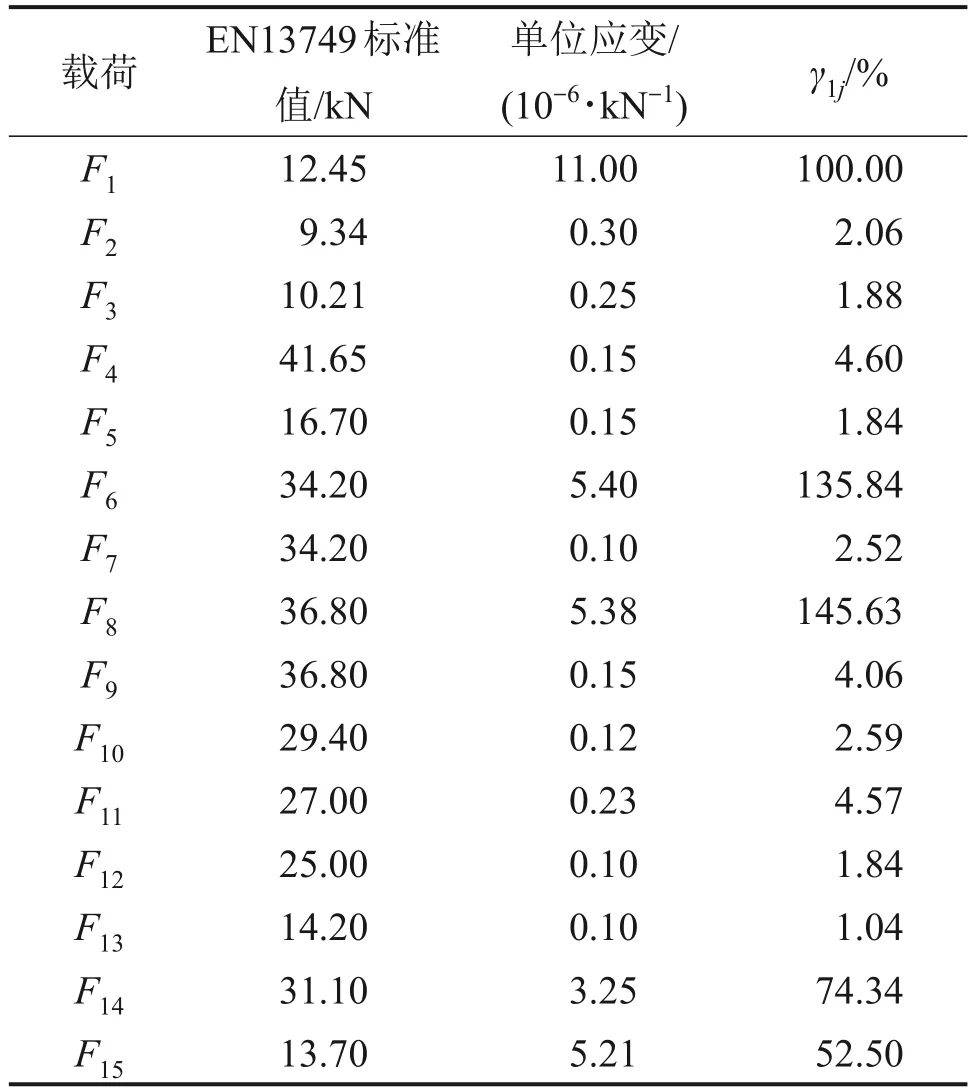
表2 浮沉载荷识别点耦合度Table 2 Coupling factor of F1 load identification point

式中:F1l,F2l,F3l和F4l分别为4个轴端的垂向载荷识别点;Fs1,Fs2和Fs3分别为实测浮沉载荷、侧滚载荷、扭转载荷。
由式(5)可知浮沉载荷、侧滚载荷表征构架整体的运动特征,而轴端作为约束,齿轮箱、电机等垂向载荷必然会对轴端载荷识别点产生影响。因此,将已解耦的载荷传递系数设为0,影响较大的载荷保留其传递系数,实现浮沉载荷识别点的降维。
从表3可以看出,其余载荷对电机垂反向载荷识别点的耦合度均在4%以内,在误差允许范围内,表明该载荷解耦效果好。因此,可将该载荷识别点除对应载荷外的载荷传递系数设为0。
对所有载荷识别点进行分析可知,除浮沉载荷和侧滚载荷识别点外,其余载荷识别点的耦合度均在4%以内,解耦效果好。同时,对浮沉载荷、侧滚载荷进行降维处理,最终得到载荷-应变传递系数矩阵K。可见除浮沉和侧滚载荷外,其他载荷实现了载荷和应变一一对应的关系,即载荷系之间实现了解耦,而浮沉侧滚载荷同样通过降维变为稀疏矩阵。

以矩阵K主对角元素为基准,对每一行进行归一化处理,可以得到:

式中:Fsi为实测载荷;Fi为标定载荷。
载荷-应变传递系数是标定载荷及其对应载荷识别点关系,只有当实测载荷等于标定载荷时,才可以正确应用载荷-应变传递系数,否则会有重复计算。根据式(7)反解标定载荷,得到浮沉载荷、侧滚载荷与其余载荷的关系:

其余载荷均实现了标定载荷和实测载荷的统一。
2.2 组合加载下载荷-应变分析
浮沉载荷识别点受电机垂同向和齿轮箱垂同向载荷影响较大,因此,选择浮沉载荷、电机垂同向载荷和齿轮箱垂同向载荷这3种载荷作为分析对象,按照表1组合加载工况进行标定试验。当同时施加浮沉载荷和齿轮箱垂同向载荷时,2种载荷识别点的应变响应值如表4所示。
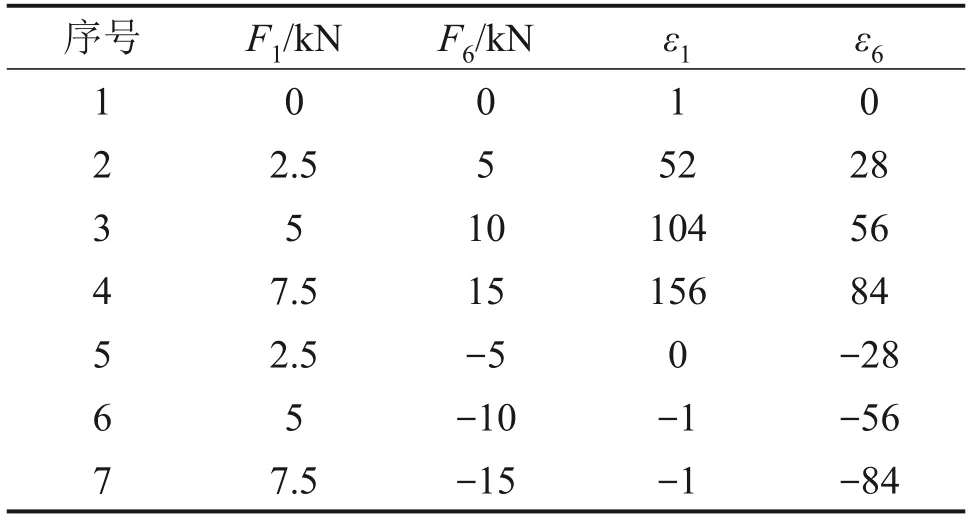
表4 浮沉和齿轮箱垂同向载荷组合加载试验结果Table 4 Test results of combined loading conditions of F1 and F6
通过多元线性回归可得2 种载荷识别点的方程为
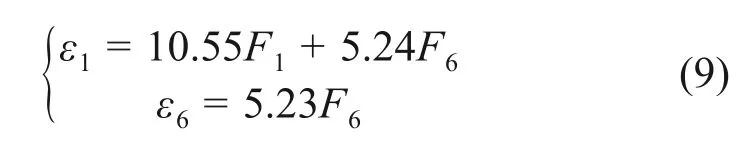
按照同样的方法,分别在浮沉载荷和电机垂同向载荷组合工况以及齿轮箱垂同向载荷和电机垂同向载荷组合工况下求解载荷应变方程为:
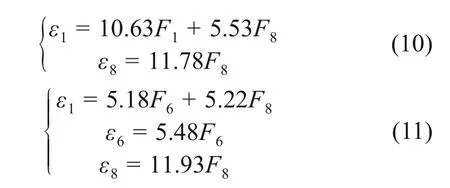
单独加载下得到的传递系数矩阵K1为

由式(9)~(11)可知,浮沉载荷识别点响应值是由3种载荷线性叠加而成,电机垂同向载荷和齿轮箱垂同向载荷识别点只受对应载荷影响,与2.1节结论一致。对比2种加载工况下得到的载荷应变传递矩阵,K2中各系数值较K1中各系数值均偏小,但在误差允许范围内,可以认为两者是一致的。
2.3 载荷应变矩阵误差分析
为对比分析载荷应变传递矩阵K1和K2的精度,按照表1的验证工况11进行加载。以3种载荷组合加载时获得的3种载荷识别点的响应值为输入,并将其与载荷-应变传递矩阵K1和K2分别代入式(2),反算加载载荷,并计算其与实际加载载荷的相对误差,结果见表5和表6。
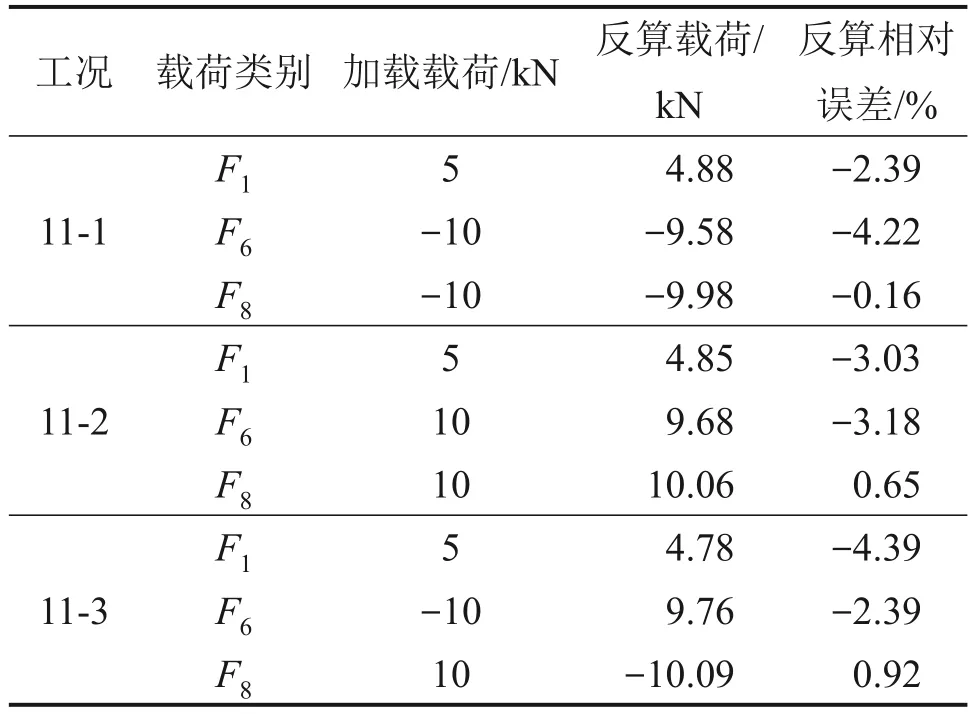
表5 K1反算载荷及其相对误差Table 5 Back-calculation load of K1 and relative errors

表6 K2反算载荷及其相对误差Table 6 Back-calculation load of K2 and relative error
由表5可知,由K1反算的浮沉载荷最大相对误差在4.39%以内,齿轮箱垂同向载荷最大相对误差在4.22%以内,电机垂同向载荷最大相对误差在0.92%以内。由表6可知,由K2反算的浮沉载荷最大相对误差在2.5%以内,齿轮箱垂同向载荷最大相对误差在1.53%以内,电机垂同向载荷最大相对误差在0.62%以内。2 种载荷应变传递矩阵相对误差均控制在5%以内,满足测试要求,表明标定结果具有很好的准确性和可靠性。K2相对误差比K1的小,表明组合加载得到的传递矩阵精度更高。
3 线路试验测试结果验证
为验证本文提出的载荷识别解耦降维标定方法效果,将标定好的构架安装于某型高速动车组上,在京沪线开展长期跟踪测试。测试仪器采用多通道数据采集系统,采样频率为2 kHz,该采样频率足以保证采样数据的完整性。
构架测试载荷必须能准确再现构架损伤,而构架损伤取决于其在运行时所受的动应力。因此,载荷预测应力能否再现实测应力可检验载荷识别的效果。根据文献[21]中典型应力测点的选取原则,本试验将构架应力区域划分为定位转臂座根部区域、制动吊座区域、电机吊座区域、齿轮箱吊座区域、横侧梁连接区域、横纵梁连接区域和抗蛇行座区域。同一区域的应力点损伤分布相似,选择每个区域中损伤值最大的应力测点作为典型测点来反映构架疲劳情况。构架典型应力测点如图3所示,图3中所标测点均是该区域的最大应力测点。典型应力测点载荷-应力传递系数见表7。
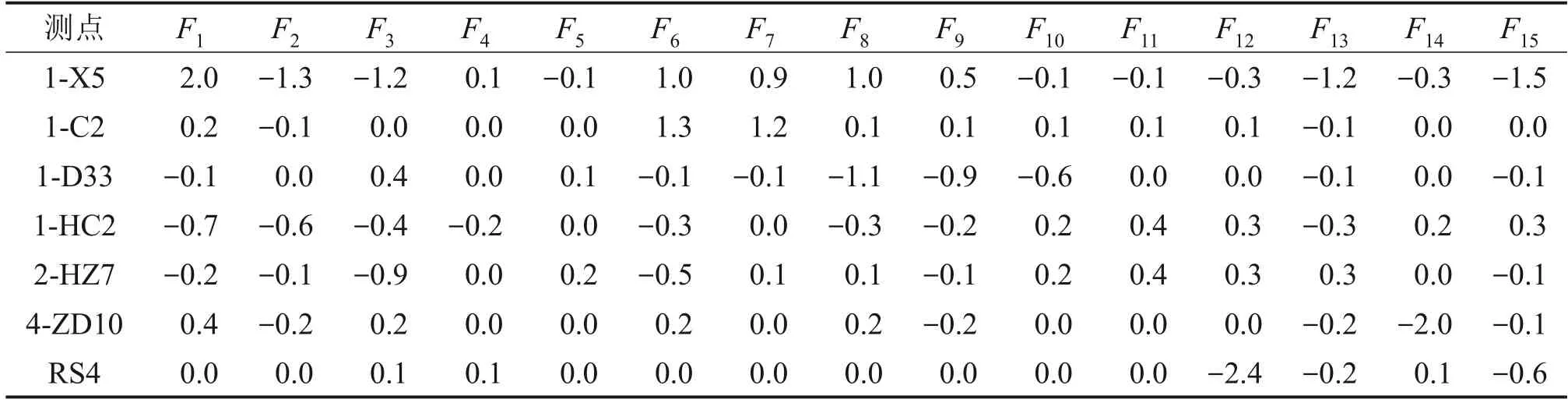
表7 载荷-应力传递系数Table 7 Load-stress transfer coefficient MPa/kN

图3 构架应力测点示意图Fig.3 Schematic diagram of frame stress measuring points
3.1 时频特征对比
载荷预测应力通过载荷时间历程乘以载荷应力传递系数获得。由于篇幅所限,以2个典型应力测点1-X5和1-C2为例进行验证,其余应力测点结果与这2 个测点一致。图4 所示为2 个典型应力测点的载荷预测应力和实测应力时间历程。从图4可以看出,2个应力测点的载荷预测应力和实测应力幅值范围相近,整体趋势基本保持一致。为了更直观对比,统计2个典型应力时间历程的时域特征值,结果如表8所示。可见,载荷预测应力与实测应力的时域特征指标很相近。
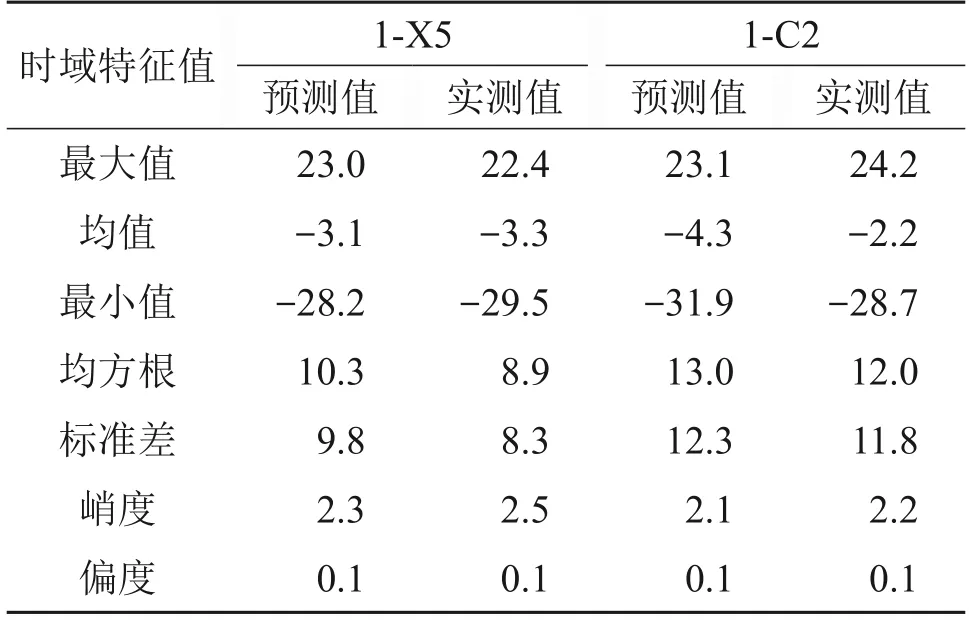
表8 载荷预测应力和实测应力特征值Table 8 Load predicted and measured stress characteristic values MPa
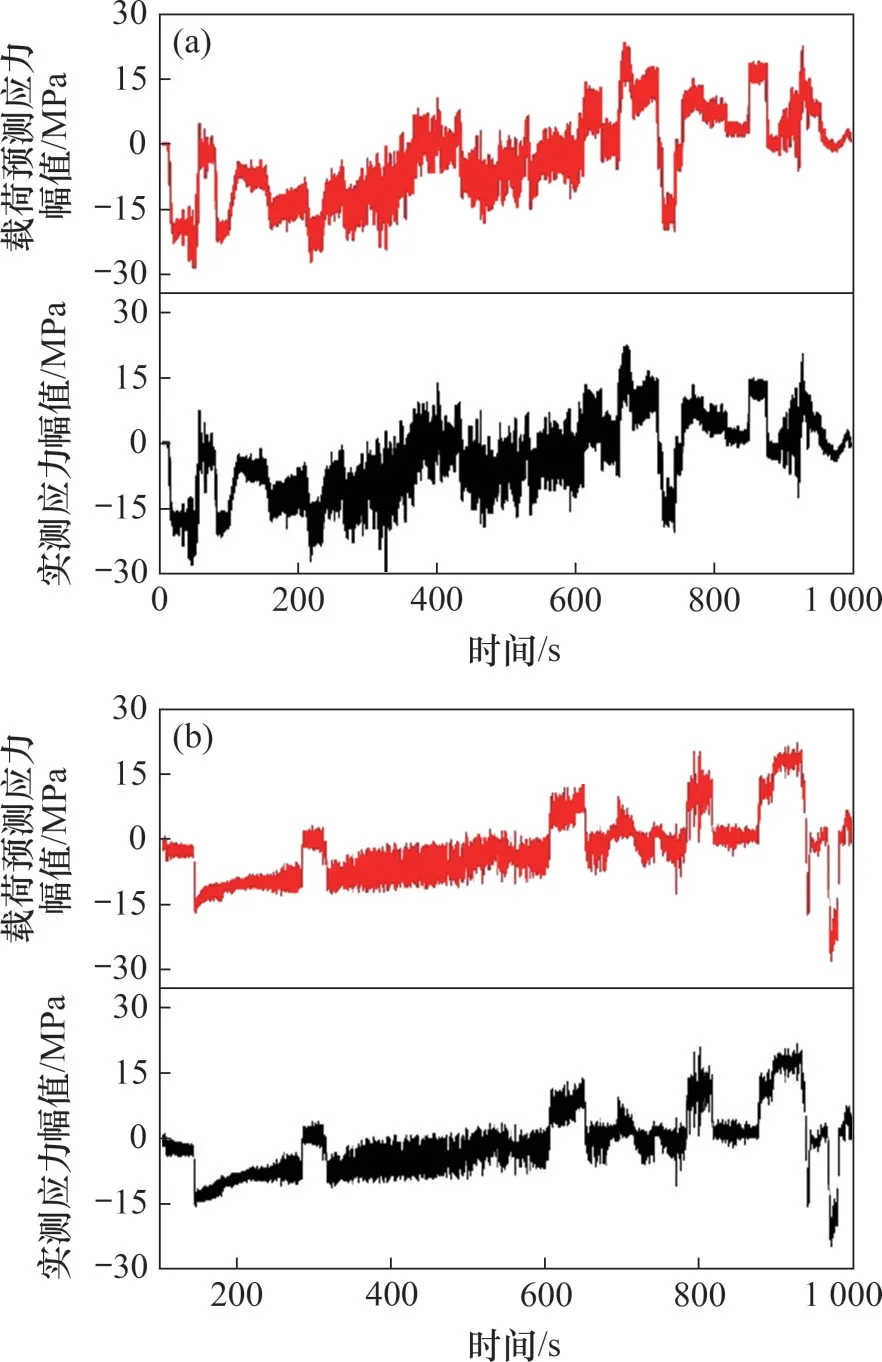
图4 载荷预测应力和实测应力时程曲线Fig.4 Load prediction and measured stress time history curves
对以上2个典型应力测点时间信号进行傅里叶变换,结果如图5所示。可见:1-X5应力测点的频率响应主要集中在10 Hz以下,1-C2应力测点的频域响应主要集中在10 Hz 以内和40 Hz 附近。2 种载荷预测应力整体变化趋势与实测应力基本相同,且能量也相近。

图5 载荷预测应力和实测应力频谱图Fig.5 Spectrum of load predicted stress and measured stress
3.2 损伤评估
构架承受变幅载荷的疲劳评估通常按照损伤当量将应力谱等效为恒幅的应力幅值,即等效应力σeq来评估,其计算公式如下:

式中:L为转向架构架在规定使用年限总运营里程,为1 500 万km;l为实测运行里程;N为等效应力对应循环次数,N=200万次;ni和σi分别为第i级应力谱对应的循环次数和幅值;m为材料疲劳属性,对于焊缝,m=3.5。
图6所示为典型应力测点的载荷预测等效应力和实测等效应力的对比。从图6可以看出,载荷预测等效应力与实测等效应力相近。两者之比均在0.81~1.16之间,相对误差不超过19%。

图6 载荷预测等效应力和实测等效应力对比Fig.6 Comparison of load predicted and measured equivalent stress
综上所述,在时域,频域和损伤等方面,载荷预测应力均与实测应力均相近,表明构架载荷解耦降维标定方法识别出的载荷结果可靠有效。
4 结论
1)利用解耦降维标定方法,使构架浮沉、侧滚载荷实现了降维,其余载荷实现了解耦,获得了精度较高的构架载荷-应变传递矩阵,进而提高了载荷识别精度。
2)构架在单独加载和组合加载下得到的载荷应变矩阵K1和K2的最大相对误差分别为4.39%和2.50%,两者反推载荷相对误差均在5%以内,满足工程测试要求,且组合加载下载荷应变矩阵K2精度更高。
3)在时域、频域和损伤等方面,载荷预测应力与实测应力更接近,载荷预测等效应力与实测应力比值在0.81~1.16 之间,最大相对误差不超过19%,证明解耦降维方法可靠有效。
