依托核心问题促进深度思考
2020-05-26张春新
张春新


复习,并不仅仅是重复先前学习的知识,而是在原有知识复习的基础上促进学生知识思维素养的再生长。生长,是夯实基础后的求异与创新。教学“平面图形面积总复习”这一课,如何在夯实平面图形面积计算的基础上让学生抓住平面图形面积计算的本质,促使其“换个脑筋”,进一步在知识的深处进行思考呢?我通过三个核心问题的引领,使学生的知识、思维、方法策略在不断被丰富、被审视、被调整的过程中得到了深度发展。
一、依托核心问题,引领学生感悟数学本质
学生的学习不能流于形式,更不能浅表化。只有抓住了所复习知识的核心问题,激发出学生积极思考的热情,促使学生深入交流、探究,才能使学生进一步地感悟到平面图形面积计算的本质,学生的学习才能触类旁通,达到“牵一发而动全身”的效果。如在學生交流了长方形、正方形、平行四边形、三角形、梯形、圆的面积推导过程之后——
师:回顾学习这些平面图形的过程,我们先学习的是什么图形的面积?
生:长方形的面积计算。
师:大家有没有想过,为什么我们先学习长方形、正方形的面积计算,然后学习平行四边形、三角形、梯形的面积计算,最后学习圆的面积计算?可不可以换一下顺序呢?请大家在小组内交流。(学生在小组内热烈地交流起来)
生:长方形的面积计算最简单。
生:长方形的四个角都是直角,其他图形没有这样的特点。
生:面积单位都是边长1厘米、1分米、1米的正方形,长方形的面积可以直接用这些面积单位去摆,从而算出面积,其他图形不行。
生:是的,长方形可以用边长1厘米、1分米、1米的小正方形去摆,看看沿着长可以摆几个,沿着宽可以摆几排,用每排的单位面积的个数×排数=总的单位面积的个数,也就是长方形的面积。而其他平面图形,比如平行四边形,用面积单位摆就不好摆满。(学生边说边在黑板上画)
生:我知道了,所以我们先学长方形的面积计算,用摆面积单位的方式推导出了长方形的面积公式,然后再学习平行四边形、三角形、梯形的面积计算,它们不好用面积单位去摆,可以用转化的思想转化成已学过的长方形来计算面积。
在以前的学习中,学生是一个图形一个图形地接着学,他们现在回过头来一看,确实先学习的是长方形的面积,为什么呢?可不可以先学习其他图形呢?学生感觉非常好奇,这激起了他们思考和探究的欲望。实际上,这也是学生思维的盲点,同时又是学习平面图形面积的核心问题。抓住了它,就抓住了面积计算的本质,即图形中所含单位面积的个数。通过对这一核心问题的思考,学生不但知道了为什么要先学习长方形面积的计算,而且对后面所学的图形计算面积为什么都要转化成已经学过的图形,也有了进一步的、清晰的认识。
这样,通过“瞻前”——对先学习长方形面积计算的这一核心问题追问,让学生回到原点思考,从源头抵其实质;同时也为“顾后”——体积度量的本质理解作了知识和方法上的铺垫。
二、依托核心问题,引导学生整体建构数学知识和思维
多维度关联是将学生所学的零散的知识根据它们内在的逻辑关系从多种角度进行统整与建构,从而让学生整体建构。
(一)以长方形面积为基础整体建构,感受由易到难的过程
通过“为什么先学习长方形的面积”这一核心问题的追问,学生从本质上理解了长方形面积的计算是其他平面图形面积计算的基础。这时,可以再让学生用图来梳理各种图形面积之间的联系。
师:通过回顾,我们知道了长方形面积公式是学习其他平面图形面积的基础,这六个图形之间是有联系的。你能用图表示出它们之间的联系吗?
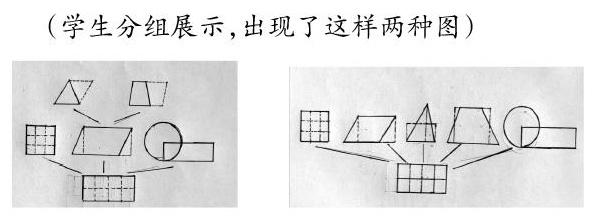
(学生分组展示,出现了这样两种图)
生:(小组1,指第一幅图)我们小组是这样梳理的,长方形的面积计算由数含有多少面积单位获得,这也是计算其他平面图形面积的基础,所以将长方形画在最下面。由长方形的面积公式推导出了正方形、平行四边形、圆的面积公式,将这三个图形画在第2层,再由平行四边形面积公式推导出了三角形和梯形的面积公式,将三角形和梯形画在最上层。
生:(小组1,指第一幅图)我来补充一下。从上往下看,三角形、梯形的面积公式是通过转化成平行四边形推导出来的,平行四边形、圆的面积公式是通过转化成长方形推导出来的,它们都不能直接用含有面积单位的小正方形去摆、去数,都巧妙地运用了转化的方法。
生:(小组4,指第二幅图)我们是这样整理的。将其他五种平面图形面积公式都转化成长方形推导出来。第1、2、3、5小组都是把三角形和梯形转化成平行四边形推导出面积公式的,我们是把三角形和梯形也转化成长方形来推导出面积。
生:(小组4)我补充。虽然我们小组之间转化的图形不一样,但共同的地方都是转化成已经学过的图形来推导出面积的,都是以长方形面积公式为基础来转化的。
(二)以梯形为中心整体建构,感受化繁为简的过程
紧扣“六个平面图形的面积都可以用梯形的面积公式计算吗”这一核心问题展开探究,可以让学生感受到其他平面图形与梯形的紧密联系。
师:前面我们以长方形的面积公式为基础推导出了其他五个平面图形的面积,由易到难。我们还能化繁为简,把这六个图形的面积公式都用梯形的面积这一个公式来计算,大家相信吗?
(学生摇头)
师:看着图形想一想,可以把这些平面图形看作怎样的梯形?
(电脑出示:梯形下底不变,上底慢慢缩短变成三角形,上底慢慢延长,变成平行四边形。)
(学生讨论交流)
生:三角形可以看作上底为0的特殊的梯形。(如下面第一个图形)
生:平行四边形可以看作上底a和下底b相等的特殊的梯形。(如下面第二个图形)
生:长方形可以看作上底a和下底b相等,且上底a、下底b与高h垂直的特殊的梯形。(如下面第三个图形)
生:正方形可以看作上底、下底和高相等即a=b=h,a、b与h垂直的特殊的梯形。(如下面第四个图形)
生:圆可以看作上底为0,下底为圆的周长即2πr,高为半径r的特殊梯形。
师:圆是封闭的曲线图形,你是怎样想的?
生:我将圆心看成梯形的上底,上底为0,将圆的一周拉直,将圆的周长(即2πr)看成梯形的下底,这时半径r就是梯形的高。
师:真不简单,能化曲为直,将圆看作这样的特殊梯形,真是爱动脑筋的孩子。
师:那么这些平面图形能用梯形的面积公式计算吗?怎么办?
生:用梯形的面积公式算算看行不行。
师:好,每人选一个平面图形算算看。计算好后,仔细观察,说说你发现了什么,然后小组内交流各自的发现。
生:我选的是三角形。用梯形的面积公式计算(0+a)h÷2=ah÷2,我发现用梯形面积公式算下来和三角形的面积公式一样。所以,计算三角形面积可以用梯形的面积公式。
生:我选的是平行四边形。用梯形的面积公式计算(a+a)h÷2=ah,我发现用梯形面积公式算下来和平行四边形的面积计算公式一样。所以平行四边形的面积可以用梯形的面积公式计算。
生:平行四边形的面积可以用梯形的面积公式计算,长方形、正方形是特殊的平行四边形,所以不需要计算,就知道长方形和正方形也可以用梯形的面积计算公式计算。
生:我选的是圆。用梯形的面积公式计算(0+2πr)r÷2=πr2 ,所以圆的面积公式也可以用梯形的面积计算公式。
生:圆也可以等积变形为梯形(如下图),所以圆的面积公式可以用梯形的面积计算。
师:现在你们想说什么?
生:梯形面积公式真神奇呀,這些图形都可以用它来计算。
这时黑板上形成的流程图如下所示:
在这一片段中,学生紧扣“六个平面图形的面积都可以用梯形的面积公式计算吗”这一核心问题展开探究。通过梯形的下底和高不变、上底变这一条件,让学生感受到其他平面图形与梯形的紧密联系。学生惊喜地发现用梯形的面积公式算下来竟然和原来图形的面积公式相同。
这样,先通过核心问题“为什么先学长方形面积”的思考,让学生感受到了平面图形面积公式由易到难的学习过程,再通过核心问题“六个平面图形的面积都可以用梯形的面积公式计算吗”的思考探究,将梯形面积公式与其他图形的面积公式勾连了起来,让学生感受到了化繁为简的惊喜。这样由易到难、化繁为简的整体建构,不再只是知识的整体建构,同时也是思维的整体建构。
三、依托核心问题,发展学生的深度数学思维
以上两个核心问题的思考探究,既使学生抓住了平面图形面积的本质,又将平面图形面积之间的关系进行了整体建构。在此基础上,还可以通过核心问题“两个图形阴影部分的面积相等吗”来促使学生进一步深度思考,灵活运用转化的思想来解决问题。
师:(出示下面两幅图)大正方形的边长为10厘米,阴影部分的面积相等吗?为什么?
生:第一个图形阴影部分左边虽然是三角形,但它的底长不知道,也很难求出。阴影部分右边部分一般用[14]圆的面积减去空白小三角形的面积,但空白小三角形的面积的底是10厘米,高也不知道,所以也不好求出。所以,我们小组思考能不能用转化的方法,把复杂的图形转化成简单的图形。
生:我们发现第一个图形中三角形ABG的面积等于空白三角形DEG的面积。把△ABG的面积移到△EDG上,整个阴影部分的面积就等于[14]圆的面积。求出[14]圆的面积,就求出了阴影部分的面积。这样就把阴影部分这一复杂的图形转化成了简单的图形[14]圆,就很好算了。
生:第二个图形也是将阴影部分这一复杂的图形转换成简单的图形。空白三角形ABE的面积是(a+b)×b÷2,梯形ABCF的面积也是(a+b)×b÷2,所以空白三角形ABE的面积等于梯形ABCF的面积。空白梯形ABGF是公共的,那么△EFG的面积等于△CBG的面积,将△CBG的面积移到△EFG上,这样阴影部分的面积就等于[14]圆的面积了。
生:两幅图中阴影部分的面积都等于[14]圆的面积,而圆的半径都是10厘米,圆的面积相等,[14]圆的面积相等,两幅图的阴影部分的面积也就相等。
师:你们真不简单。在常用的方法无法解决问题的情况下,想到了运用转化的策略来解决。
生:平面图形面积推导的过程给了我们启示,在推导平行四边形、三角形、梯形等面积公式时,都是转化成我们已经学过的简单的图形来推导的。
生:是的,当计算较复杂的平面图形面积时,如果无法直接计算,我们就可以换一种思路,看看能不能将较复杂的不规则图形转化成简单的规则图形来求。
本教学片断中,核心问题“阴影部分的面积相等吗”激起了学生探究的热情。因为常用的整分法(大面积减去多余的小面积)和分割法(将复杂的阴影部分分割成几个小的规则的图形)都无法解决,所以这种思维困境激起了学生进一步挑战该问题的强烈欲望。学生通过进一步思考,想到了运用转化的策略可以将复杂的阴影部分转化成简单的图形。怎样转化呢?学生小组内继续思考,他们积极寻求面积相等的图形,发现了图形之间的关系,将阴影部分的一小部分图形面积移到了与之面积相等的空白部分上,就转化成了简单的图形[14]圆,问题也就迎刃而解了。
此外,这节课以猜平面图形的游戏开始也以同样的游戏作为结束。这种游戏就是一个学生说,另一个学生猜。比如,猜长方形。课前,学生都是说它的特征(两组对边相等,四个角都是直角)而让其他的学生猜。课终,还是长方形,再猜,说法就多了:是其他平面图形的基础,是学习的第一个平面图形,可以用表示面积单位的小正方形去摆求出面积;是上底下底相等,且上下底和高垂直的特殊的梯形等。这样,通过课始和课终猜平面图形的游戏,既激发了学生学习的兴趣,又让学生感受到了通过一节课的学习所带来的知识思维生长的喜悦。
(责任编辑:杨强)
