基于非线性扩张状态观测器的四面固支板自抗扰振动主动控制

朱超威, 李生权, 李 娟, 曹晴峰

(扬州大学电气与能源动力工程学院, 江苏 扬州 225127)

汽车工程、船舶工程和航天工程中常用的固支板结构易受外界环境激励产生共振和疲劳破损, 故其振动控制尤为重要[1-3]．Nguyen[4], Hasheminejad[5]等分别采用构造简单的线性二次最优控制(linear quadratic gaussian, LQG)和速度反馈的线性方法实现了振动抑制, 但该类方法依赖于精确的数学模型．Ma[6]假定干扰源可测, 采用自适应滤波法进行降噪减振,能迅速跟踪结构参数和外扰响应的变化．宋哲等[7]则将智能控制方法应用于结构振动控制方面,经训练后的神经网络能有效抑制悬臂梁的振动．本课题组前期设计的构造简单且无需精确数学模型的线性自抗扰控制[8-10](linear active disturbance rejection control, LADRC)很好地实现了振动控制,但观测器的线性化产生的峰值现象一定程度地降低了其观测精度; 因此, 本文拟利用非线性fal函数构建非线性扩张状态观测器(nonlinear extended state observer, NESO)以期提升控制器的观测性能, 获得更好的振动控制能力．

1 模态分析及数学模型

模拟飞机蒙皮, 构建尺寸为500 mm×500 mm×1 mm的四面固支板(all-clamped plate, ACP)．由于ACP的边界条件复杂, 常用的有限元分析方法存在的建模误差易使压电元件的布置位置选择不当而导致观测溢出和控制溢出[11]．为了精确获得ACP的固有振型, 利用激光多普勒测振仪对其进行模态分析．首先在ACP反面安装惯性作动器,给予作动器10～1 000 Hz的扫描频率信号,激励ACP振动．当扫描频率信号与ACP的固有频率一致时, 二者产生共振, 此时通过PSV-500激光测振仪(polytec公司,德国)采集该振动信号并反馈至模态分析仪进行处理, 得到ACP某阶的模态频率及其模态振型,如图1所示．在图1中该阶模态振型的最大应变处以同位配置原则粘贴压电片作为驱动器和加速度计作为传感器, 以取得较好的振动控制效果．

假设粘贴了压电驱动器的整个结构具有线弹性,并在共振处采用单自由度的质量阻尼弹簧模型描述系统,则该系统动力学数学模型[8]为

(1)

其中m,r,k分别为ACP的模态质量、模态阻尼和等效刚度;y为ACP运动位移;F为外界激振力;αV为压电片逆压电效应产生的作用力,α为力因子,V为施加电压．

将式(1)转换为状态空间表达式:

(2)

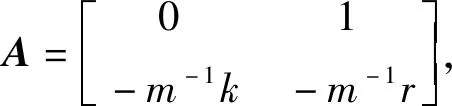
据文献[8]知, 当压电智能结构在固有频率附近发生振动时,可采用如下等式进行系统辨识:

(3)

其中λ为施加电压与振动位移之比,C0为压电片固有电容,f0为压电片短路共振频率,f1为压电片开路共振频率,ε为结构阻尼系数．本文参数测量值为λ=9 223 V·m-1,C0=105.3 nF,f0=104.942 Hz,f1=105.355 Hz,ε=0.063．

2 自抗扰振动主动控制器设计

将式(3)代入式(2),得到系统的状态方程

(4)

(5)

式中f(x1,x2)为系统模型信息,b为控制器增益,w为不确定的外部干扰．由于系统参数的测量误差不可避免, 故令b0估计b, 使模型误差f(x1,x2)+(b-b0)u作为内部扰动, 则总扰动为f(x1,x2)+(b-b0)u+w．

令x3=f(x1,x2)+(b-b0)u+w, 假设扩张的状态量x3可微, 则h=d[f(x1,x2)+(b-b0)u+w)]/dt, 系统可描述为

(6)

忽略z3和x3的估计误差, 令u=u0-z3/b0, 有

(7)

系统经式(7)的动态补偿转变为积分串联型系统,对z1,z2设计传统的PD控制器, 其控制率u=-kpz1-kdz2-z3/b0, 其中kp为比例增益,kd为微分增益．于是本文所设计控制系统的结构如图2所示, 其中D/A表示将数字信号转换为模拟信号的数模转换，A/D则反之;V为数字信号u经D/A转换后得到的模拟信号，即式(1)中的施加电压; NI PCIe-6343为具有A/D和D/A功能的数据采集卡．

3 实验验证

3.1 实验平台搭建

以尺寸为500 mm×500 mm×1 mm的四面固支板结构为原型, 搭建一套如图3所示的实验平台, 验证本文所提控制方法的有效性．通过PSV-500激光测振仪分析得到ACP的固有振型．在振型应变的最大处粘贴尺寸为40 mm×10 mm×1 mm的压电片, 以获得更好的控制能力．在ACP右侧布置HEV-20激振器(南京航空航天大学振动工程研究所, 南京)模拟外部干扰激励．CA-YD-160型IEPE加速度传感器采用同位配置的原则贴合于压电片, 将产生的信号采用YE3821型IEPE电流源适调器放大10倍, 经NI PCIe-6343采集功能(输入范围为-10～10 V)传送到Matlab/Simulink中desktop real-time环境下的Analog Input模块. 随后通过所设计的控制器产生控制量, 并将该控制量传送到Analog Output模块, 经NI PCIe-6343控制功能产生实际电压信号(输出范围为-10～10 V)．此信号经HVP-300D功率放大器放大至-110～110 V后, 驱动压电片抑制外部激励干扰．

3.2 振动控制结果

为了更好地分析本文自抗扰控制器的振动抑制性能, 选用105 Hz的信号激励四面固支板,分别采用无控制和基于非线性ADRC的结构振动控制进行对比实验．控制器的参数选择如下:kp=100,

kd=2.5,b0=80,β01=100,β02=200,β03=350,δ1=δ2=0.01,α1=α2=0.01．分别采集如图4所示的控制前后的时域振幅, 并对其进行快速傅里叶变换(fast Fourier transform, FFT), 结果如图5所示．

图4显示,该模态未加控制前,时域中结构的振幅为1.25 V, 而在增加本文所设计控制器后振幅缩减为0.15 V,幅值减少了88%,说明该控制器对外部干扰有较强的振动抑制作用．由图5可知, 由于加速度计与压电驱动器没有完全同位配置, 致使420 Hz左右的模态被激发,但其幅值较低, 仅为-35 dB, 故该频率的模态溢出可忽略不计．而在共振频率为105 Hz处,幅值削减明显,故放大该频率下的FFT图,如图6所示．

由图6可见, 在该模态下的共振幅值由1.969 dB下降至-14.98 dB, 共减少了16.949 dB, 说明本文设计的非线性自抗扰控制器针对结构的振动具有很强的控制能力．采集如图7所示的施加电压, 仅为-80～80 V, 说明激光测振仪的实验模态分析可有效优化传感器与驱动器的位置配置,自抗扰控制器的控制效率和控制效果能得到有效提升．