基于两阶段参考点三层选择的多目标优化算法

徐立龙, 李二超

(兰州理工大学电气工程与信息工程学院, 兰州 730050)

多目标进化算法(multi-objective evolutionary algorithms, MOEAs)已广泛应用于现实生活中, 如: 盲源分离[1]、流水车间调度[2]、物流配送[3]等, 但算法的运行效率、收敛性、多样性等方面的效果不佳; 因此, 研究者对多目标进化算法提出了各种改进措施．针对NSGA-Ⅱ中的非支配排序存在大量解重复比较的情况, Zhang等[4]提出一种有效的非支配排序(effective non-dominated sorting, ENS)以提高运算效率, 但随着目标维数的增加, 运算效率会降低; Yuan等[5]提出基于θ占优的进化算法, 通过将解分配到分布均匀的参考点对应的类中, 且仅比较同类中解的占优关系, 从而增加了Pareto最优解的选择压力, 并保证解的分布性, 该算法同时考虑分布性与收敛压力, 但未考虑分类过程计算量大的问题,降低了运算效率; Luo等[6]提出一种计算资源的分配更新策略来提高运算效率, 但改进较小的个体时会导致种群多样性丢失; 韩红艳[7]提出两层PBI(penalty-based boundary intersection)聚类策略, 分别通过个体到权重向量的垂直距离和个体在权重向量上的投影距离解决多样性和收敛性问题, 以聚类后每类中的优秀个体为聚类中心, 距离聚类中心最近的个体重新聚为一类; Li等[8]将基于聚合函数分解和基于Pareto占优的方法结合, 充分利用两种方法的优势, 权衡算法的收敛性和多样性但未考虑聚类过程的计算复杂度; Zhou等[9]提出一种新的PBI聚合方法, 即利用每个解到超平面之间的垂直距离代替解在参考向量上的投影距离, 与传统的PBI聚合方法相比,该算法收敛速度快,但是该算法聚类过程计算成本过大,运算效率不高．本文在文献[9]的基础上, 提出一种基于两阶段参考点三层选择的多目标优化算法(multi-objective evolutionary algorithm for two-stage reference point three-hierarchy selection, TT-MOEA)．

1 TT-MOEA算法

1.1 聚类

个体的目标函数值f(X)距离所有参考向量中垂直距离最小的参考向量归类于该参考向量, 可用基于惩罚边界交叉[6,9]公式F(X)=di,1+θdi,2表示, 其中F(X)为个体的聚合函数值,di,1是个体在参考向量上的投影距离,di,2是个体到参考向量的垂直距离, 预设参数θ>0, 并用个体到超平面[9-10]的垂直距代替投影距离, 聚类原理如图1所示．

转换公式为F(X)=θdi,2-dL, 其中dL为个体到超平面的垂直距离, 为使F(X)取最小值, 须满足

(1)

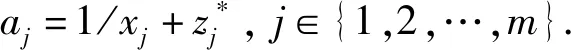
1.2 参考点的生成

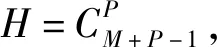
1.3 两阶段策略

本文以代数的前一半与后一半分为前期与后期, 前期因设置的参考点少而形成少量的参考向量,此时聚类起到的多样性作用不大,故前期以Pareto支配的快速收敛作用为主;后期的参考点较多,形成的参考向量会形成更多的聚类领域,聚类前首先对个体的目标函数值进行归一化处理,使得参考向量均匀分布在截距为1的超平面上,并在每个聚类领域内再进行小生境选择,在稀疏领域中添加个体, 从而增加种群的多样性．

1.4 三层选择策略

三层选择思想如图3所示．父代种群经交叉变异产生子代种群, 将子父代种群合并, 经ENS排序, 根据非支配等级将其分为3类, 若前L-1层的个体数为q, 未达到种群个体数N, 则要添加第L层的个体, 使种群个数大于等于N, 此层称为临界层．将大于L层的个体删除, 选出大于种群个数的优秀个体数U,此层主要是为了加速收敛．再将ENS选出的临界层作为第2次选取种群, 对其进行聚类操作,每一类个体求其PBI聚合函数值,将每类中最小聚合函数值的个体视为第1层F1, 依次类推有{F2,F3,…},原理如图4所示．同理, 根据PBI依次选取种群并将其分为3类, 若前w-1层所选个体数目P<(U+q)-N, 则再添加第w层个体, 使P≥(U+q)-N, 此时将大于w层级的个体删除．二次选出临界层个体的数目为K, 综合考虑收敛性与多样性, 对PBI选出的K个个体使用小生境选择, 选出N-(P+q)个优秀个体, 主要为了增加多样性, 最终使得下一代个体的数目等于初始种群个数．

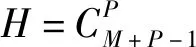
2 测试函数与评价指标

为验证TT-MOEA算法的性能, 选取T-MOEA(不含两阶段策略的本文算法)、NSGA-Ⅱ[12]、MOEA/D[13]、MOEA/D-TCH[14]、NSGA-Ⅲ[15]5类算法对测试函数DTLZ[16]与ZDT[17]进行计算, 通过运行时间与多种性能指标来比较不同算法的计算效果．

2.1 测试函数及参数设置

ZDT1～ZDT3测试函数目标之间相互冲突,即存在一增一减的关系．DTLZ2测试函数的目标相关性如图6所示．从图6可以看出, 测试问题满足Pareto最优边界时, 对应着属于XM的所有xi=0.5, 可得g(XM)=0, 使得决策变量在同一范围内变化; 取x1=x2, 则表达式为f1(X)=cos2(x1π/2),f2(X)=0.5sin(x1π),f3(X)=sin(x1π/2)．DTLZ7测试函数的目标相关性如图7所示．从图7可以看出, 满足Pareto最优边界条件使XM=0时,g(XM)=1, 取其特殊关系判断, 即x1=x2, 表达式等价于f1(X)=f2(X)=x1,f3(X)=6-2f1(1+sin(3πf1))．

相关参数选取[9]: 交叉指数m=30, 变异指数mm=20, 变异概率Pm=1/V, 交叉概率PCR=1.0, 惩罚因子θ=5, 差分进化参数F=0.5, 并设置两阶段参考点阈值为G/2代．求取参考点个数时,第一阶段设置两目标参数P=2, 三目标参数P=4; 第二阶段设置两目标参数P=N-1, 三目标参数P=23, 计算出与种群个数相同的参考点．本文设置算法循环代数为250, 两目标种群个数为100, 三目标种群个数为300, 决策变量数为V=M+9．

2.2 评价指标

1) 运行时间表示算法从初始化到程序运行结束的总时间．

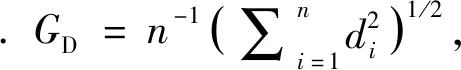
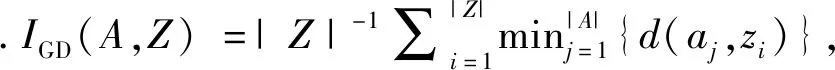
3 结果与讨论

本文TT-MOEA算法与上述5类算法在标准测试函数上得到的评价指标列于表1, 图8为部分仿真结果．测试结果显示: 1) 本文算法在ZDT3上运行时间最短, 而在其他测试函数上MOEA/D-TCH算法效率较高; 同时在两目标上本文算法效率较高, 三目标上MOEA/D-PBI算法效率较高; 总之, 在每个测试函数上本文算法运行效率优于T-MOEA算法, 表明聚类过程是使算法运行效率降低的重要环节．NSGA-Ⅱ次之, NSGA-Ⅲ由于复杂的框架结构导致运算效率最慢．2) 由GD值可知, MOEA/D算法除ZDT2测试函数外均好于其他算法,结合仿真图可以看出, 对于不连续函数, MOEA/D算法只是个体的局部收敛性能好; NSGA-Ⅲ在不连续Pareto前沿与ZDT2上表现较好, 本文算法次之, NSGA-Ⅱ算法最差． 3) 由S值可知, 除在测试函数ZDT1上本文算法表现较好, 其他测试函数上T-MOEA算法表现最好, 本文算法次之．这是因为本文算法前期考虑收敛性, 设置了较少的参考点, 使聚类效果减弱,导致种群多样性变差,使本文算法略弱于T-MOEA算法．4) 由IGD值可知, 除MOEA/D-PBI算法在测试函数ZDT1上表现较好,在其余测试函数上MOEA/DTCH算法表现最好, NSGA-Ⅲ算法次之; 在连续测试函数上, MOEA/D-PBI算法与MOEA/DTCH算法略好于本文算法;在Pareto前沿不连续测试函数上本文算法较好,NSGA-Ⅱ算法最差．由标准测试函数的仿真结果与性能指标表明,本文算法针对多目标优化,对于凸凹问题都适用,通过比较测试函数ZDT1与ZDT2的IGD值可知,整体优化更适用于凹问题．

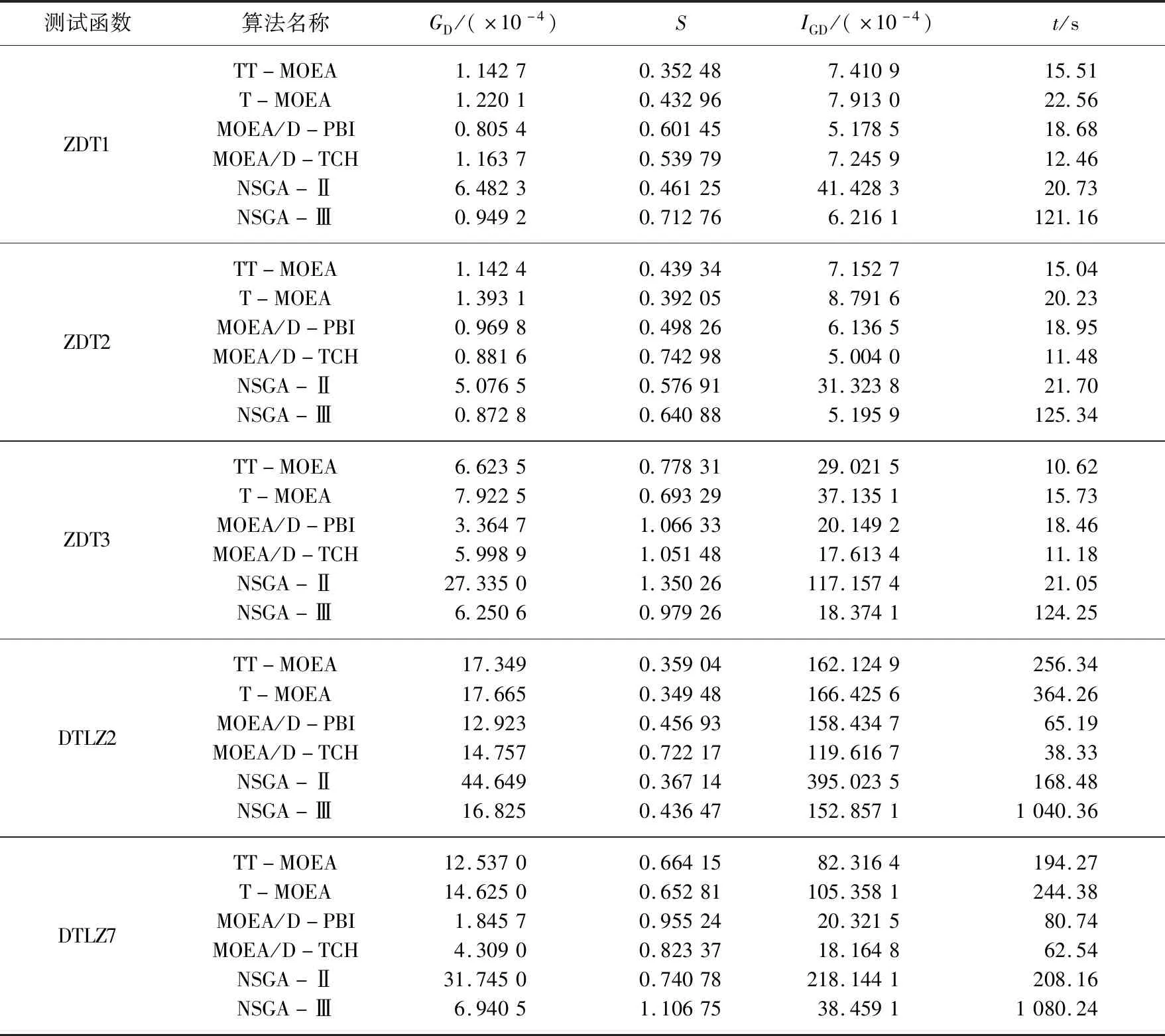
表1 不同算法求解标准测试函数所得的评价指标和t值