基于改进分布估计算法的作业车间调度

戴 敏, 张玉伟, 曾 励, 竺志大, 张 帆

(扬州大学机械工程学院, 江苏 扬州 225127)

由于先进制造技术与物联网、云计算、雾计算、大数据等信息技术的迅猛发展, 智能制造模式成为制造业的重要发展方向[1-2]．生产车间调度作为智能制造系统的重要环节, 其调度效率是制造系统智能化水平的重要体现,而作业车间调度(job-shop scheduling problem, JSP)是生产车间的一种代表性调度类型．JSP可描述为[3]: 假设存在n个任务组成的任务集T={T1,T2,…,Tn}和m台机器组成的机器集M={M1,M2,…,Mm}, 每个任务Ti有Ni道工序, 所有工序按照规定的加工工艺路线在m台机器上完成操作．调度目标是确定每台机器上工序的排列次序, 以实现生产指标(完工时间、生产成本等)效率最优化．同时生产调度过程满足以下假设: 1) 所有任务和机器在0时刻均可进行操作; 2) 同一任务的工序间有先后约束关系; 3) 每台机器在任意时刻只加工1道工序; 4) 工序不可中断．JSP本质上是NP完全问题(non-deterministic polynomial hard, NP-Hard), 其求解方法分为精确算法和近似算法2类[4]．精确算法在求解小规模问题上具有一定优势, 但随着问题规模的扩大,近似算法的求解优势较显著．分布估计算法(estimation of distribution algorithm, EDA)作为近年兴起的一种近似算法在车间调度问题研究方面备受关注[5]．张守刚等[6]对硫化车间调度进行研究,设计了一种离散的分布估计算法求解调度问题;肖世昌等[7]提出一种混合分布估计算法对随机工时的作业车间调度问题进行了研究．EDA是一种基于概率模型的广度搜索算法, 但在深度优化方面容易陷入局部最优．模拟退火算法(simulated annealing,SA)自从1953年被提出以来就广泛应用于各个领域,Laarhoven等[8]首次使用SA求解JSP问题;Akram等[9]通过快速模拟退火与淬火相结合的方法改进SA算法,并通过JSP标准案例验证改进算法的有效性．虽然SA算法深度搜索能力显著,但是采用单点迭代搜索效率较低．

本文综合EDA和SA的优点,提出一种改进的分布估计算法(enhanced estimation of distribution algorithm, EEDA)求解作业车间调度问题．首先,针对JSP设计基于概率模型的分布估计算法对问题进行广度搜索,获取优良解集; 然后, 采用模拟退火算法对选择优良解进行深度搜索;同时,基于激素调节机制设计新的模拟退火函数,进一步加强算法搜索能力．

1 EEDA算法设计

EEDA算法的流程如图1所示．首先, 设定算法的各种参数和终止条件,根据研究问题的特点给出概率模型公式及其更新机制;其次,计算完工时间作为适应度值,并对适应度值进行排序;然后,基于关键路径的状态生成函数形成新群体Sj, 并设初始迭代参数i=0;最后,基于模拟退火准则并设计新的退火函数来判断个体优劣,从而保留更多优秀个体,并计算适应度值来寻求最优解．

1.1 基于关键路径的状态生成函数设计

状态生成函数的设计首先要确保SA产生的候选解尽可能遍布全部解空间,本文采用基于关键路径的领域结构设计状态生成函数: 设A,B是两个可行解, 若B是通过移动A的某关键块中除首尾工序外的任一道工序至该关键块工序之前或之后得到的可行解, 则B是A的邻域,由此获得的邻域较小．

1.2 概率模型构建及更新机制

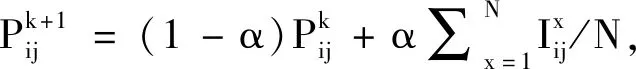
1.3 基于模拟退火函数设计

在模拟退火温度更新操作中,一般采用函数Tk+1=λTk(0<λ<1)来控制温度的退火速度, 式中Tk+1表示当前退火温度,Tk表示上一次退火温度．采用这种方法, 温度下降速度完全取决于λ值的选取, 实际过程中动态选值难度较大,且低温阶段难以获取更多优秀个体．在人体血糖调节行为中,激素调节规律函数具有较好的收敛性, 使胰岛素与胰高血糖素能快速达到动态平衡,保持人体的正常血糖水平．受此启发, 本文根据激素调节规律(即Hill函数分布规律)[10], 提出新的退火函数调控SA的温度更新, 其表达式为Tk+1=ε/(1+kn)-kΔTexp(-k), 式中常量系数ε一般取初始温度值,k为迭代次数,n为Hill函数系数, ΔT为当前温度与上一次温度的差值．

2 数值试验与结果分析

2.1 参数敏感性分析

在EEDA算法设计中参数设置直接影响算法性能, 重要参数包括种群大小NIND、最大迭代次数max、学习率α和Hill系数n．本文以10个任务在10台机器上进行加工, 每个任务包括10道工序的随机事件为例进行测试, 表1给出了不同的参数设置对平均完工时间的影响．由表1可知, 增大NIND, max和α均会缩短平均完工时间．值得注意的是无限增大上述任一参数值, 均会牺牲算法的运行时间, 因此应合理选择参数, 本文取NIND=20, max=2 000,α=0.5．此外, 由表1中可见当n=2时能求解平均完工时间的最优值或近似最优值．

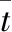
表1 算法的不同参数设置对平均完工时间的影响

2.2 性能分析

为了验证EEDA算法性能的有效性, 本文对2类基准事件进行测试: Fisher和Thompson设计的事件FT06,FT10,FT20; Lawrence设计的事件LA01～LA40．EEDA算法与其他文献中的EDA算法、SA算法、分布差分进化算法(EDA-DE)、遗传退火算法(GA-SA)、 基于优先级规则的遗传算法(P-GA)、 种群规模分别为40和60的基于移动瓶颈的遗传算法(SBGA-40/60)、 种群初始化类型分别为参数化、无延迟和主动初始种群的混合遗传算法(HGA-Param/HGA-Non-delay/HGA-Active)的比较结果如表2所示．表2显示在43个测试事件中通过EEDA算法能获得30个事件的最优解,求解质量明显高于SA、EDA算法．与文献中的相关算法相比,EEDA在求解基准问题上更具优势．

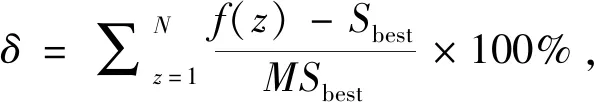
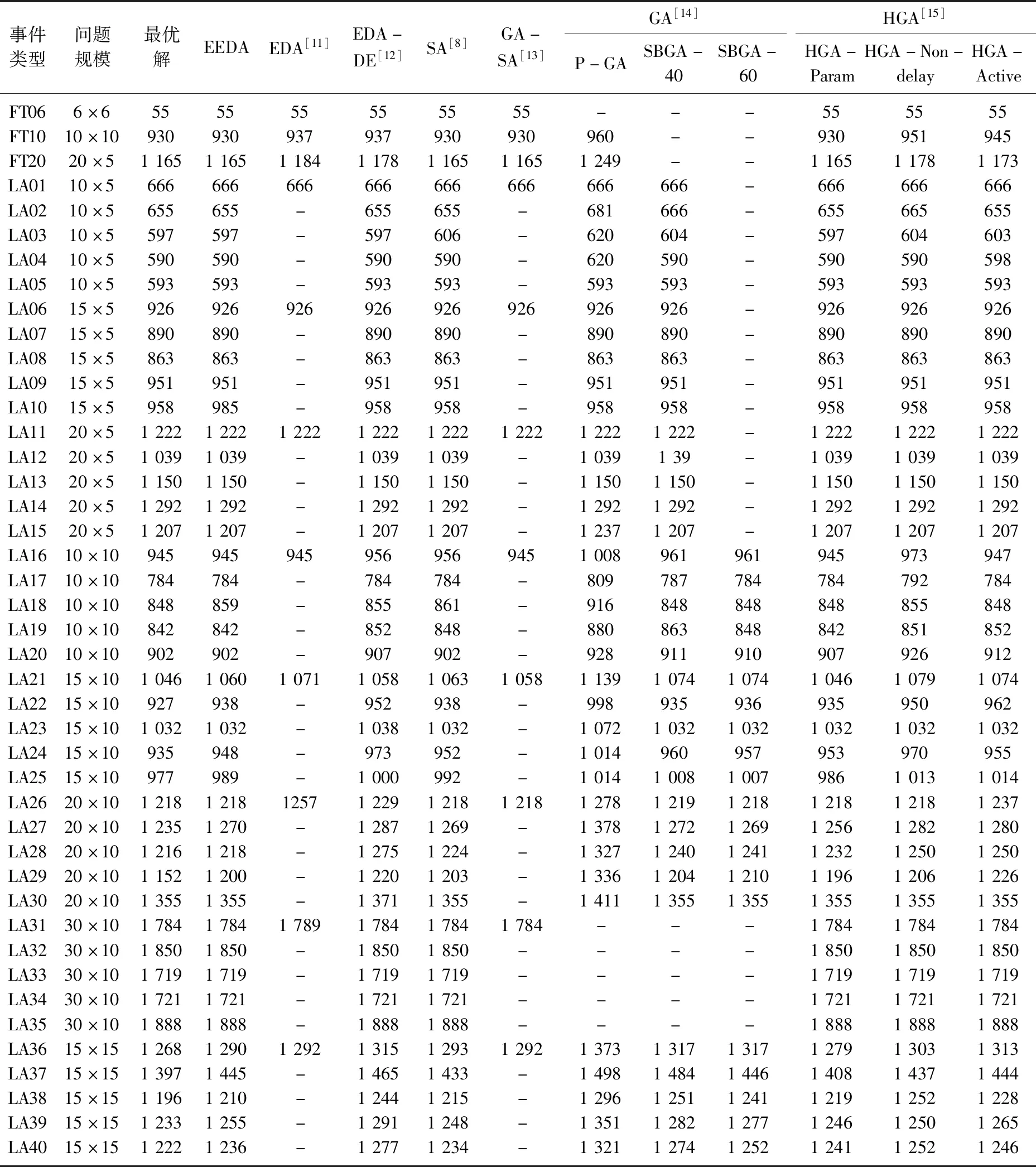
表2 不同算法的试验结果

表3 EEDA和其他算法相比较的试验结果