基于实测荷载的铁路钢桁梁桥疲劳可靠性评估

肖 鑫，赵欣欣

(1.中国铁道科学研究院集团有限公司铁道建筑研究所，北京 100081；2.高速铁路轨道技术国家重点实验室，北京 100081)

1 引 言

钢结构疲劳一直是钢桥中重点关注的问题，由于桥梁结构在服役期内会受到荷载、自然灾害以及人为因素等影响，不可避免地产生损伤累积，当达到一定程度时，往往会在没有明显征兆的情况下突然断裂，严重威胁列车和行人安全。因此，如何准确评估钢结构的疲劳一直是国内外研究的热点。

钢结构的疲劳评估方法最早始于1945年Miner[1]提出的Palmgren-Miner线性累积损伤理论，随后，经过一系列试验，确定了一些典型构造细节的 S -N 曲线，奠定了疲劳分析的基础，经过不断发展，形成了较为成熟的基于 S -N 曲线的疲劳分析方法。Paris[2]提出了著名的Paris公式，为疲劳裂纹寿命计算提供了一个全新的方法，促进了断裂力学与疲劳分析的结合，打开了基于断裂力学疲劳分析的大门。以往对钢结构的疲劳分析大都采用上述两种确定性的方法。然而，钢结构的疲劳破坏是一个非常复杂的问题，受到众多因素的影响，而这些因素又具有较强的随机性，因此，逐步形成了基于可靠性的钢结构疲劳评估。从20世纪80年代开始，国内外学者对此进行了大量的研究，并建立了一系列基于 S -N 曲线和断裂力学的钢结构疲劳可靠性评估方法[3-8]，这些方法中，疲劳应力谱是其中的制约因素。

疲劳应力谱除直接采用监测数据获得之外[9]，还可采用确定性的典型疲劳车辆或采用随机车辆加载求得。其中随机车辆加载考虑了车辆荷载参数的不确定性，与确定性疲劳车辆加载相比更符合实际情况。文献[10,11]建立了基于WIM数据的疲劳车辆模型，由于该模型中车辆模型具有确定的参数，在疲劳可靠性分析中受到一定限制。Guo等[12]则利用WIM实测数据建立了车辆概率模型，并应用于正交异性钢桥面板的疲劳可靠性评估。罗媛等[13]建立了随机车流模型，提出了基于随机车流的桥梁疲劳应力谱模拟方法，并据此分析了桥梁疲劳可靠性。王达等[14]根据建立的随机车流模型，对桥梁斜拉索疲劳可靠性进行了分析。文献[15-17]也详细介绍了基于随机车流的桥梁疲劳可靠性评估方法。可以看出，国内外对于公路桥梁的随机车流模型研究较多，并建立了一系列基于随机车流模型的桥梁疲劳评估方法。但针对铁路桥梁的基于随机荷载模型的疲劳可靠性研究还较少。

鉴于随机车辆荷载模型的不确定性，且为了更符合实际运营情况，本文以一铁路钢桁梁桥实测车辆荷载数据为基础建立随机车辆荷载模型，结合 Monte -Carlo 法生成的随机车辆荷载，分析了构件疲劳应力谱,并研究了桥梁构件与系统疲劳可靠性。

2 随机车辆荷载模型

某下承式铆接铁路钢桁梁桥，桥梁结构如图1所示，单线线路，客货共运，桥上列车通行繁忙，为实时观测桥梁的运营性能，于2016年安装健康监测(Structural Health Monitoring)系统，监测桥梁结构响应与列车通行状况，其中，列车通行状况的监测包括车速、轴重和编组。

随机车辆荷载模型是基于长期监测数据，考虑列车轴重、速度和编组等随机变量而建立的。与典型疲劳车辆荷载模型相比，随机车辆荷载模型考虑了车辆参数的概率特征。不仅可用于模拟车辆多个参数的随机性，而且可考虑车辆荷载变化对疲劳应力谱的影响。

该桥客货共运，列车的构成主要包括机车和车辆，而对疲劳应力谱产生影响的主要因素包括列车类型、机车的轴重、轴数及类型、车辆的轴重、编组及类型以及列车的运行速度。因此，可将随机列车荷载模型表示为

F=f(c,l,n,v)

(1)

式中c表示列车类型(客车或货车)，l表示机车(包括轴数及轴重)，n表示车辆(编组数量及轴重)，v表示运行速度。模型中各参数的概率分布可参见文献[18]。

3 基于随机车辆荷载的桥梁构件疲劳可靠性评估

3.1 疲劳极限状态方程

该桥为铆接钢桥，选用AASHTO LRFD Bridge Design Specification 2017规范中的疲劳细节C进行分析，相应的 S -N 曲线为

(Δσ)n=(A/N)1/3

(2)

式中 (Δσ)n为应力幅值，A为疲劳强度系数，A=14.40×1011MPa3,N为应力循环次数。

根据Miner线性累积损伤理论，累积损伤指标D可表示为

图1 钢桁梁桥

Fig.1 Steel truss bridge

(3)

式中 Δσi为第i个疲劳应力范围，ni为应力范围Δσi的循环次数。

桥梁实际运营中，疲劳应力多为变幅应力，在应用S -N曲线对桥梁进行疲劳评估时，可对应力历程进行雨流计数，根据疲劳损伤等价原则，将变幅应力等效为等幅应力循环。

根据式(2,3)，以日等效应力为基本计算单位，桥梁在服役期y(年)内的疲劳累积损伤可表示为

(4)

式中 Δσe为日等效应力幅，Ne为日等效应力幅对应的日循环次数。

当结构发生疲劳时，根据累积损伤准则，可将疲劳极限状态方程表示为

(5)

式中D0为结构的疲劳临界损伤。由于在计算中所采用的数据均来自传感器，或多或少都存在一定的误差，Frangopol等[19]提出了修正系数e，对监测数据进行修正。且在实际状况中，该桥为单线线路，每天通行的车辆数变化不大，因此，可将疲劳方程(5)写为

(6)

式中 Δσv为每列车的等效应力，Nv为等效应力幅Δσv对应的循环次数，T为每天通行的列车数。AASHTO LRFD 2017规范中规定了每种疲劳细节的常幅疲劳极限CAFL，对于常幅荷载，当细节所受疲劳应力幅小于CAFL时，认为细节不产生损伤，对于变幅应力，可将0.5CAFL视为疲劳极限，而国内外研究表明，应力幅中小于常幅疲劳应力的中低疲劳应力幅仍有一定的疲劳损伤作用，因此，本文偏于安全考虑，认为所有疲劳应力幅都会对结构产生损伤。

3.2 疲劳可靠性分析方法

疲劳可靠性分析中，疲劳应力谱是其关键。目前，对疲劳应力谱的分析多采用影响线加载。为考虑随机车辆荷载的作用，本文提出了一种基于随机车辆荷载模型的疲劳可靠性评估方法，其分析流程如图2所示。(1) 采用 Monte -Carlo 法根据建立的随机车辆荷载模型生成随机车辆荷载； (2) 建立桥梁有限元模型，求得各构件的应力影响线； (3) 将生成的随机荷载在构件应力影响线上进行加载，求得应力历程； (4) 采用雨流计数法，根据S -N曲线求得等效应力与相应的循环次数； (5) 建立应力谱概率模型，根据极限状态方程计算构件疲劳可靠指标。

图2所示流程实现了基于随机车辆荷载的疲劳可靠性评估，以随机车辆荷载作为输入，考虑了车辆荷载的不确定性对疲劳应力谱的影响。由 Monte -Carlo 法得到的随机车辆荷载模型，在样本数量足够大时足以反映实际车辆荷载的分布特征。

3.3 疲劳极限状态方程参数分布

疲劳极限状态方程(6)中，共包括疲劳临界损伤、等效应力、应力循环次数、疲劳强度系数、修正系数以及车辆通行数六个参数。

疲劳荷载效应分布包括等效应力Δσv以及应力循环次数Nv。采用上述疲劳可靠性分析方法，以下弦杆H5H6与斜杆H8B9为例，对其等效应力Δσv以及应力循环次数Nv进行分析， 结果如 图3 和图4所示。可以看出，等效应力与应力循环次数均呈现单峰分布，经检验，下弦杆H5H6的等效应力与应力循环次数可分别采用正态分布和对数正态分布进行描述，而斜杆H8B9的等效应力与应力循环次数均可采用正态分布描述，具体分布参数列入表1。

文献[20，21]对大量的疲劳试验数据进行分析，发现Miner临界疲劳损伤度D0服从对数正态分布，并假定其均值为1，变异系数为0.3。参考文献[3]，假设疲劳强度系数A服从对数正态分布，变异系数取为0.45。而对于e的概率分布，国内外并无太多研究，根据文献[19]，假定其服从均值为1，变异系数为0.03的对数正态分布，经统计分析，该桥每日列车通行数量服从正态分布。各参数的具体分布列入表2。

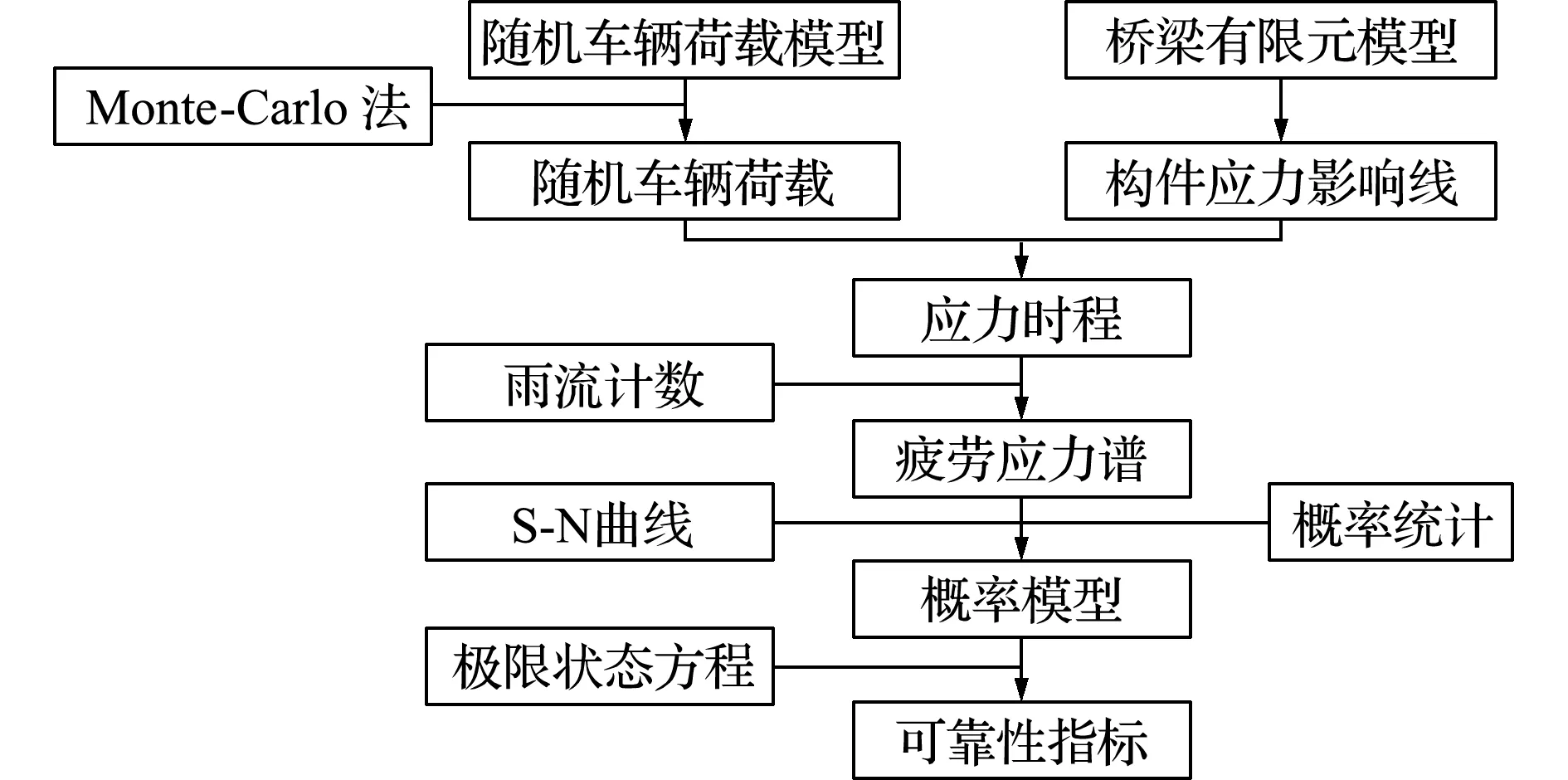
图2 疲劳可靠性分析流程

Fig.2 Fatigue reliability analysis process

表1 疲劳荷载效应分布参数

Tab.1 Distribution parameters of vehicle load effect

构件项目分布类型均值变异系数H5H6等效应力正态分布14.6270.194循环次数对数正态分布1.1190.458H8B9等效应力正态分布14.0820.217循环次数正态分布16.1730.172

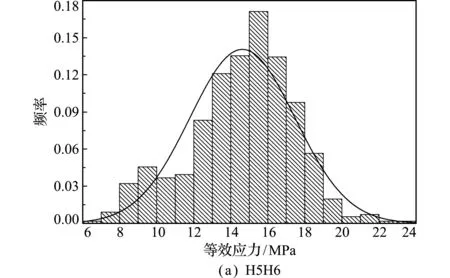
图3 构件等效应力分布

Fig3 Equivalent stress distribution of components

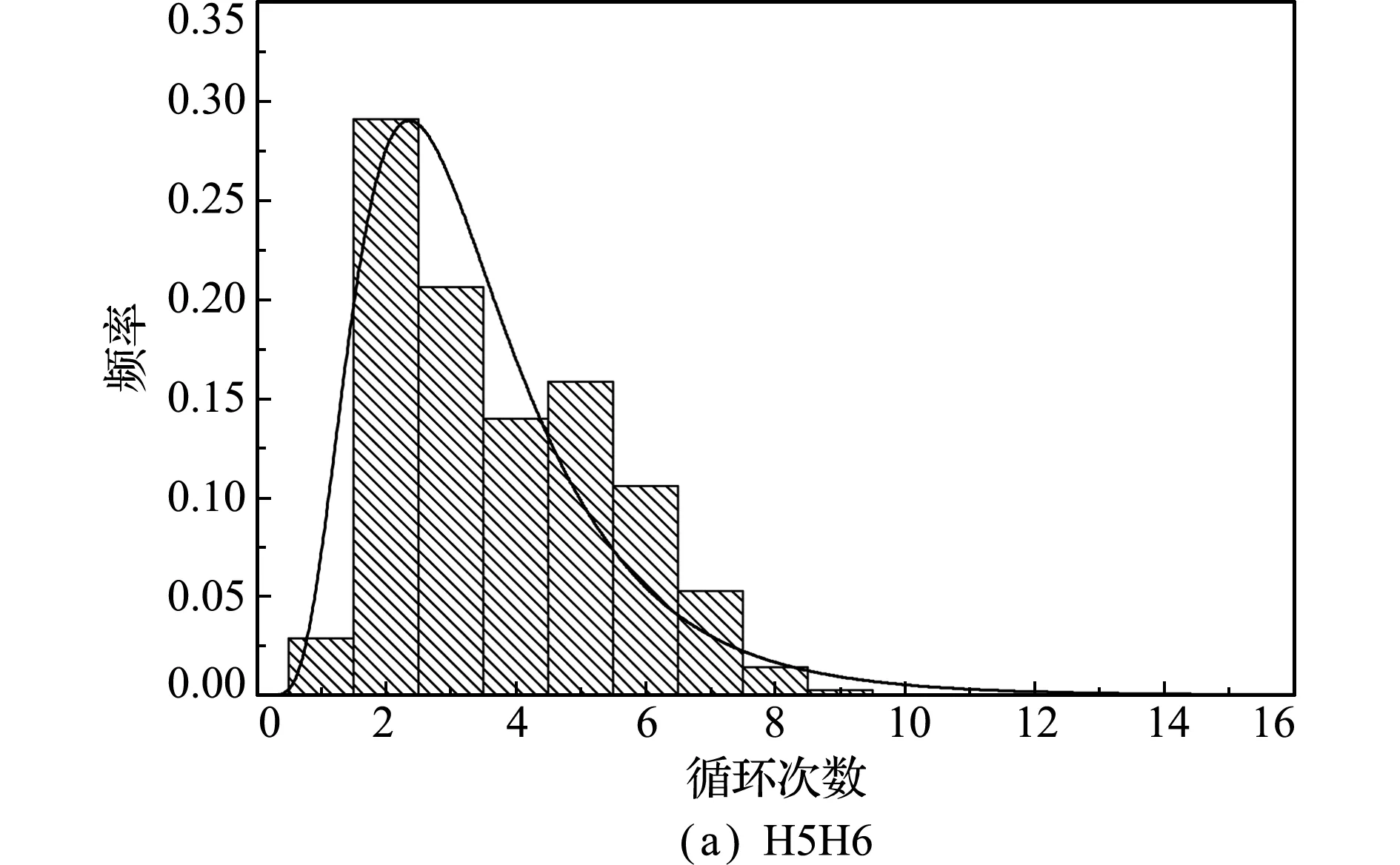
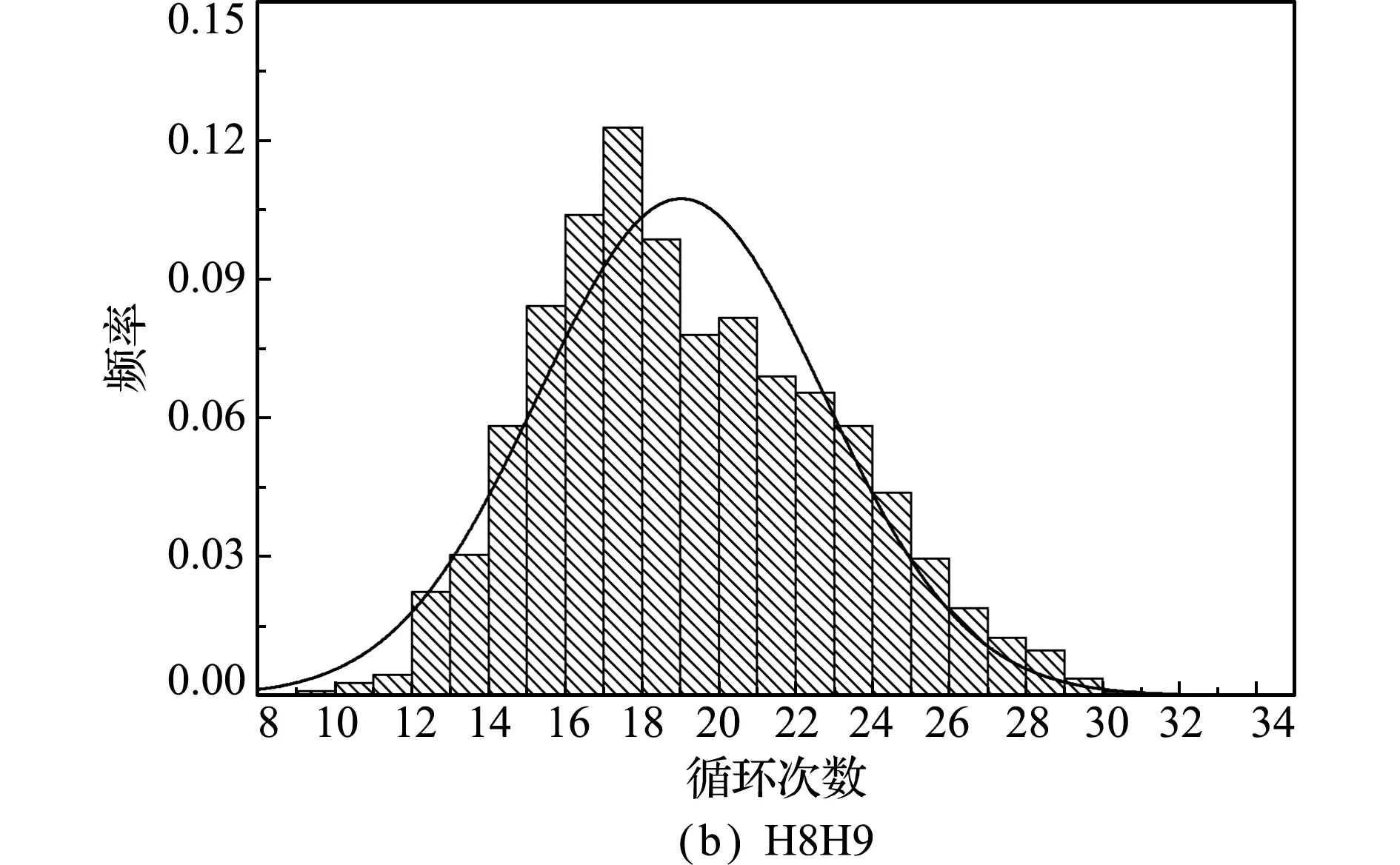
图4 构件应力循环次数分布

Fig4 Stress cycle number distribution of components

3.4 构件疲劳可靠性分析

目标可靠指标的确定是进行可靠性评估的重要前提，国内外学者对其做了较多的研究，但并无统一的标准，参考文献[22]，为合理评估该铆接钢桥，本文取疲劳目标可靠指标为2.0。根据式(6)，计算杆件H5H6与H8B9运营200年的疲劳可靠性变化，结果如图5所示。可以看出，在运营初期，疲劳可靠指标变化较大，随着运营时间的增长，可靠指标变化趋于平稳，斜杆H8B9的疲劳寿命较小，在运营141年后达到疲劳极限。

3.5 相关因素对疲劳寿命的影响

上述对于疲劳寿命的评估都是基于运营过程中车辆荷载不发生较大变化为前提，而在实际过程中，随着运营年限的增加，通行的列车荷载会发生一定变化，这将影响车辆荷载效应，最终影响结构疲劳。

3.5.1 车辆荷载增长对疲劳寿命的影响

同时，调研报告“建设宜章扶贫科技产业园区，培育莽山战略性新兴产业体系”也颇显眼。莽山是世界级的动植物基因库，是一篇大文章。要贯彻落实新发展理念，放大莽山生态优势，用现代科技重新武装宜章农业发展，培育莽山绿色生态生命科技战略性新兴产业体系。

式(6)给出了未考虑车辆荷载增长的疲劳极限状态方程，式中T表示每日通行列车数量，在此，将列车荷载的增长表示为每日列车通行数量的增加，则相应的疲劳极限状态方程可写为

[1+(y-1)·a]

(7)

式中a为列车荷载增长系数，在此取a=1%～5%。以斜杆H8B9为例，计算服役200年内疲劳可靠指标随a的变化情况,结果如图6和表3所示。可以看出，随着车辆荷载的增加，疲劳寿命逐步减小，在使用初期，车辆荷载的增加对疲劳可靠度的影响较小，随着运营时间的增加，影响逐步加大。当车辆荷载增长率达到5%时，斜杆H8B9的疲劳寿命从141年减小到44年，可见车辆荷载的增加会大幅减小构件的疲劳寿命。

表2 其余参数分布

Tab.2 Distribution of other parameters

项目分布类型均值变异系数临界损伤对数正态分布10.30疲劳强度系数对数正态分布14.40×10110.45修正系数对数正态分布10.03通行车辆数正态分布1110.06

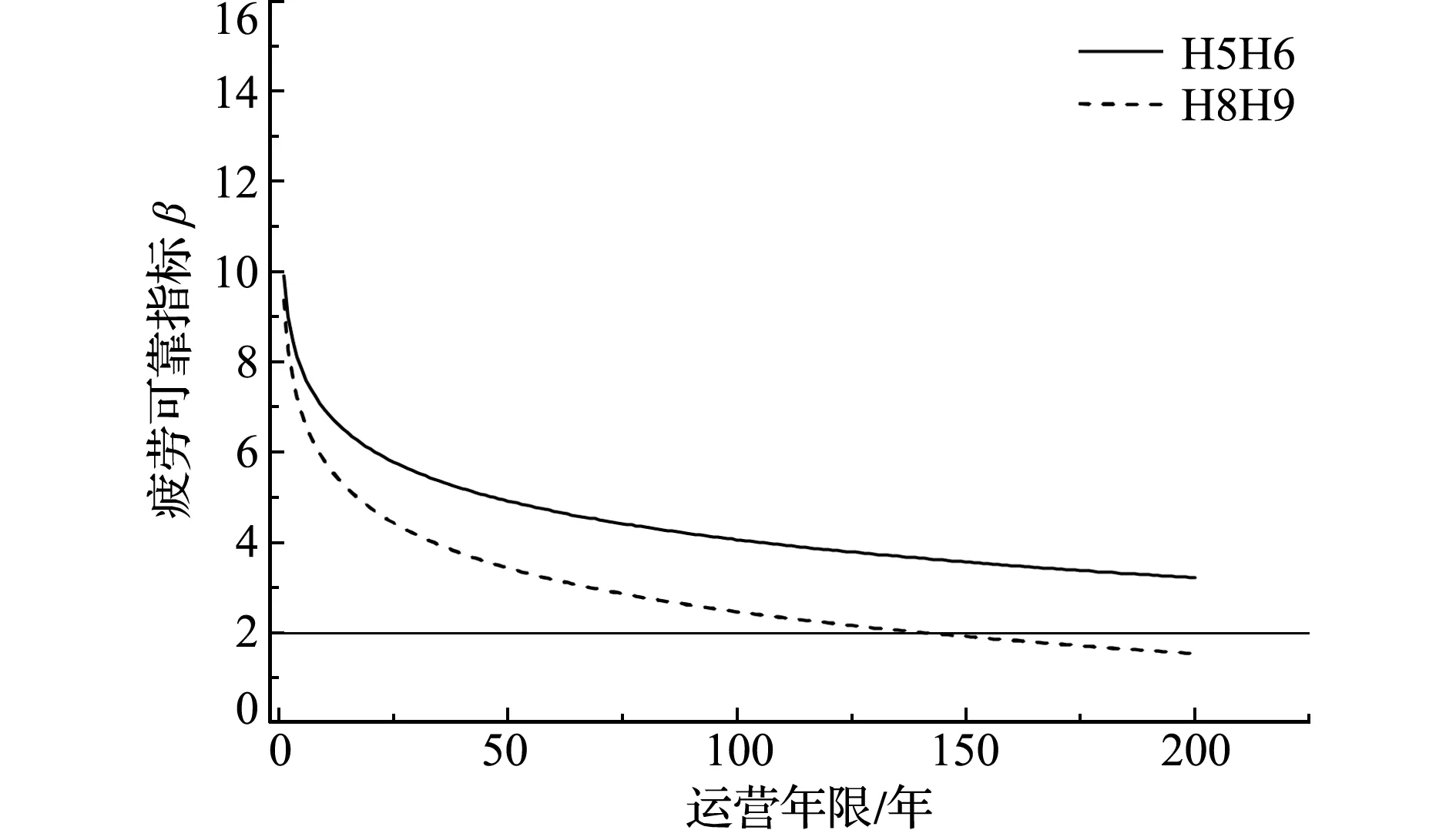
图5 构件疲劳可靠指标变化

Fig.5 Variation of components fatigue reliability index

3.5.2 车辆荷载效应变异性对疲劳寿命的影响

从上述分析可以看出，车辆荷载效应(等效应力与循环次数)变异系数较大，均在0.1以上。由于该桥客货共运，车辆荷载效应复杂多变，在对其进行疲劳评估时，有必要分析车辆荷载效应的变异性对疲劳寿命的影响。仍以上述斜杆H8B9为例，分别分析等效应力与循环次数的变异系数从0.1增加到0.5时疲劳寿命的变化，结果如图7～图9所示。可以看出，随着车辆荷载效应变异系数的增加，疲劳寿命减小，当等效应力的变异系数从0.1增加到0.5时，斜杆H8B9疲劳寿命从198年减小到61年；而当循环次数的变异系数从0.1增加到0.5时，斜杆H8B9疲劳寿命从144年减小到118年，可见疲劳寿命对等效应力的变异性更加敏感。

表3 斜杆疲劳寿命

Tab.3 Fatigue life of inclined rods

荷载增长率/%012345疲劳寿命/年1417962554844

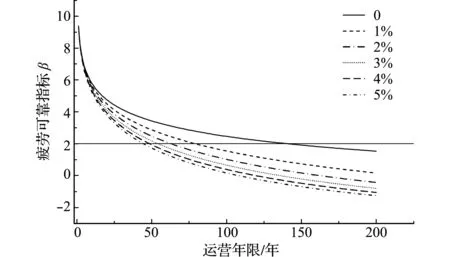
图6 疲劳可靠指标随列车荷载增长的变化

Fig.6 Variation of fatigue reliability with train load

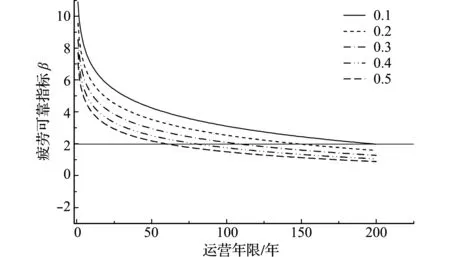
图7 疲劳可靠指标随等效应力变异性的变化

Fig.7 Variation of fatigue reliability with equivalent stress variability

综上所述，车辆荷载量和车辆荷载效应变异性的增加都会减小构件的疲劳寿命，因此，在对钢桥进行疲劳评估时，应重点关注实际通行的车辆荷载情况。

4 桥梁系统疲劳可靠性分析

结构由诸多构件组成，单个构件的失效不一定会使整个结构失效。对构件进行的可靠性研究只是结构的一种失效模式，因此，为准确地对结构进行可靠性评估，进行系统可靠性的研究是十分必要的。系统可靠性分析中，无论一个结构多么复杂，都可看作是一系列失效模式组成的串联系统，任一失效模式的发生都将导致整个结构失效，因此，要研究结构的系统可靠性，最为重要的是确定其失效模式。本文采用β约界法确定失效模式，约界公式采用文献[23]提出的半经验公式：

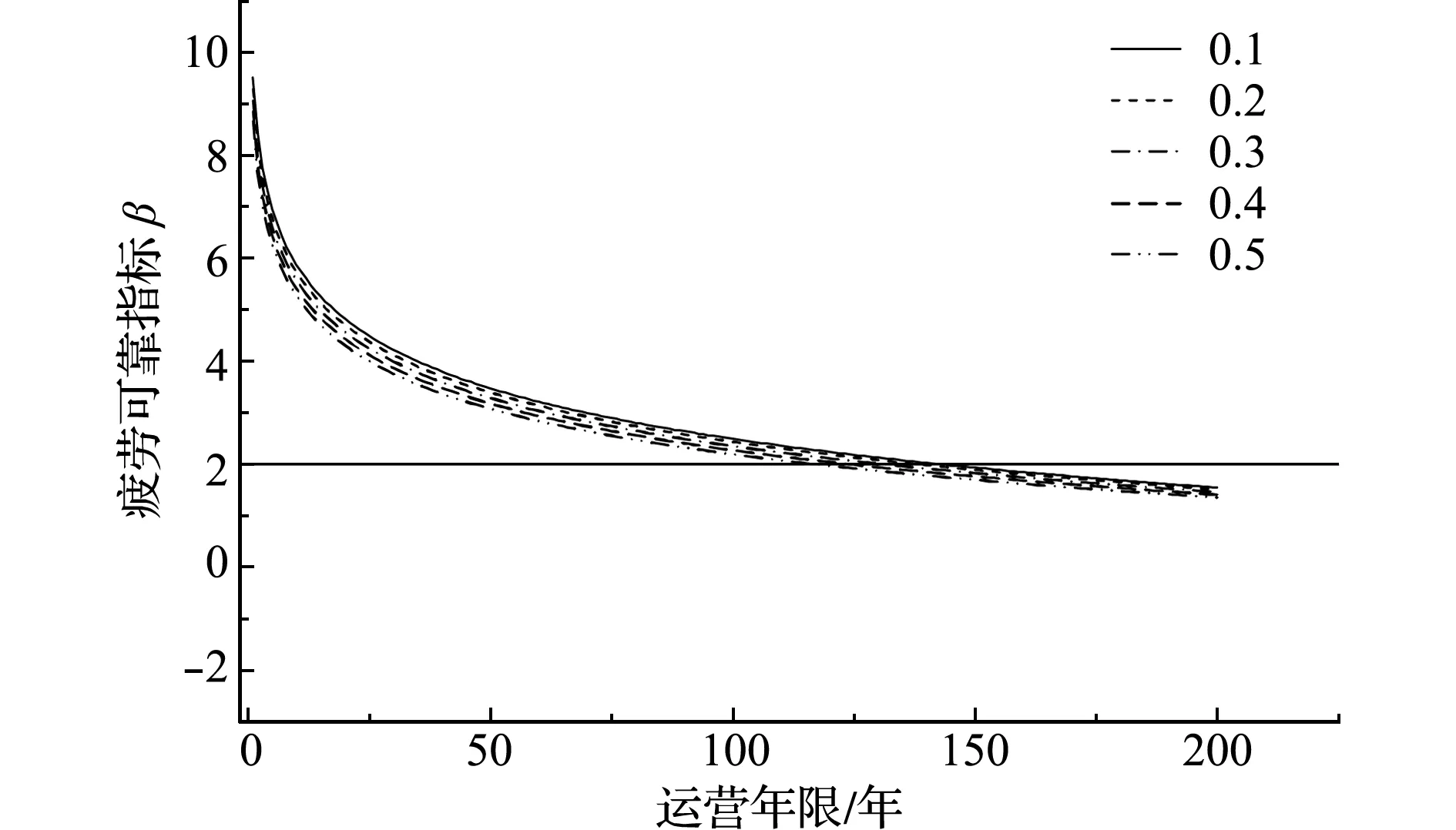
图8 疲劳可靠指标随循环次数变异性的变化

Fig.8 Variation of fatigue reliability with stress cycle number variability

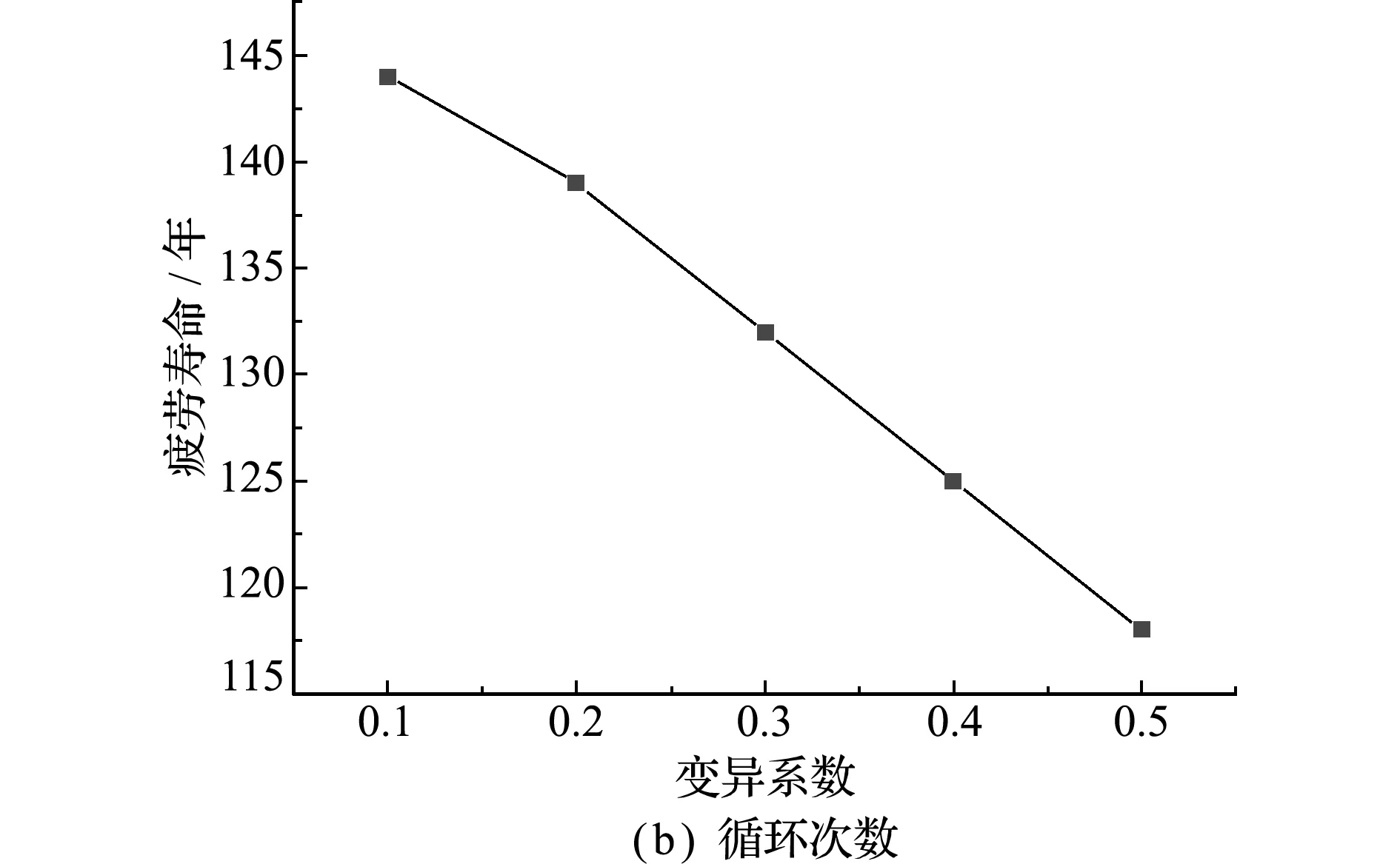
图9 疲劳寿命随荷载效应变异性的变化

Fig.9 Variation of fatigue life with load effect variability

(8)

桥梁当前运营63年，根据式(6)求得的各重要构件的疲劳可靠指标列入表4。其中，斜杆H8B9的可靠度最小，根据式(8)，相应的约界值为

β1=1.29+0.86×3.1088=3.9636

根据β约界法，其中，斜杆H6B7及H8B9均为失效候选单元，偏保守地认为全桥8根这类型的杆件均为第一失效候选单元，由于各斜杆均为重要杆件，则共有8种实效模式，根据串联系统失效概率计算方法，当前系统失效概率pf=0.005，则系统疲劳可靠指标β=2.5758。

根据上述计算方法，该桥系统疲劳可靠指标随服役时间的变化如图10所示。可以看出，系统疲劳可靠指标小于构件疲劳可靠指标，取目标可靠指标为2.0，则该下承式钢桁梁在运营86年后达到疲劳极限，与单个构件的疲劳寿命相比，系统疲劳寿命偏低，但更为合理。

表4 重要构件疲劳可靠指标

Tab.4 Fatigue reliability of important components

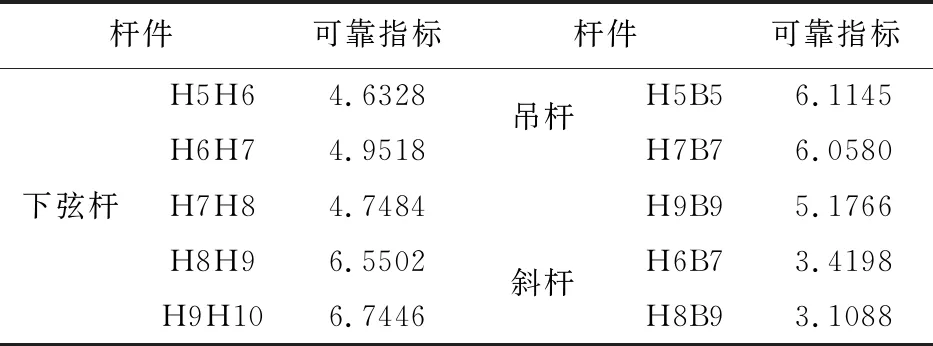
杆件可靠指标杆件可靠指标H5H64.6328吊杆H5B56.1145H6H74.9518H7B76.0580下弦杆H7H84.7484H9B95.1766H8H96.5502斜杆H6B73.4198H9H106.7446H8B93.1088

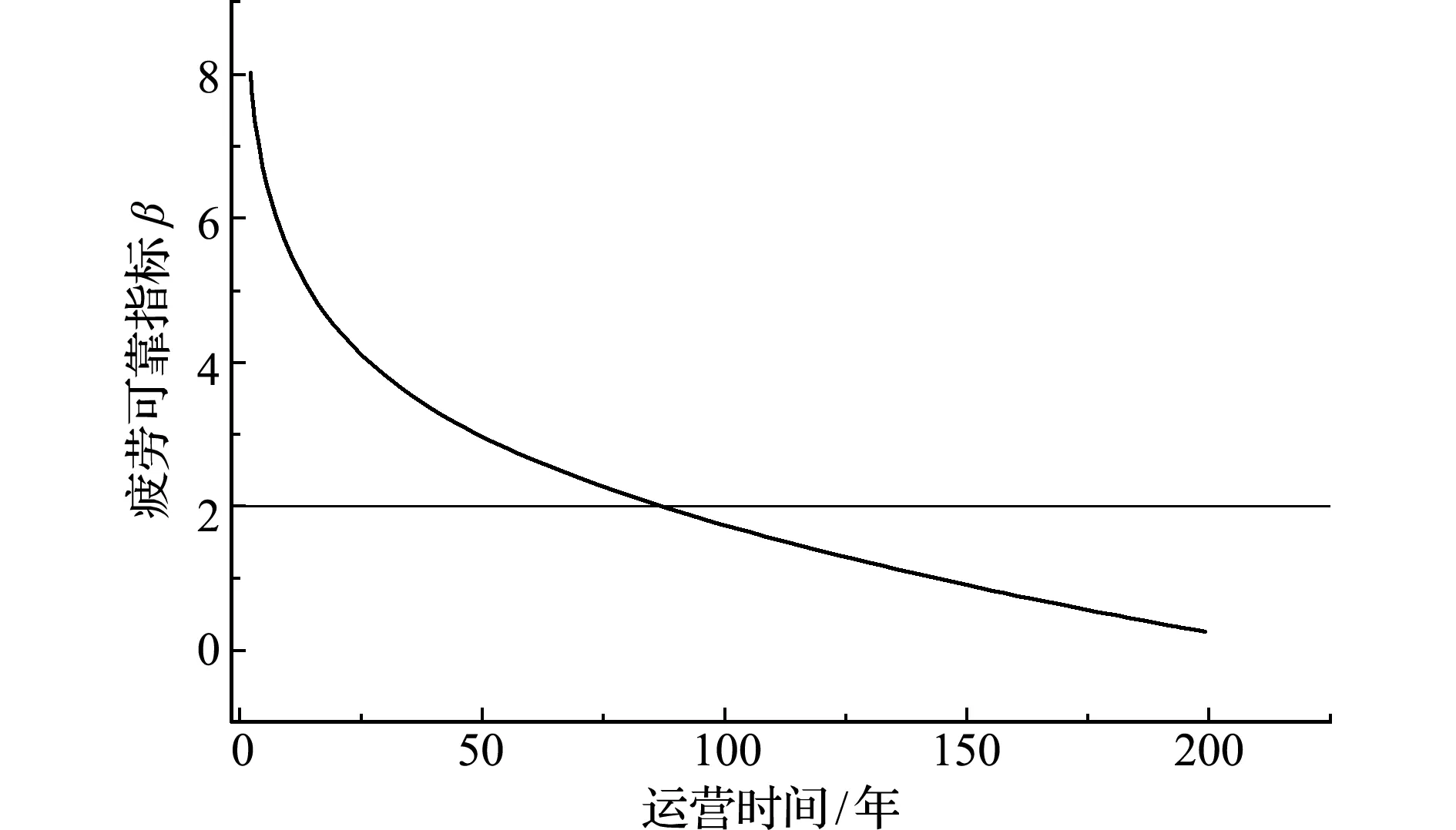
图10 系统疲劳可靠指标随时间的变化

Fig.10 Variation of system fatigue reliability with time

5 结 论

(1) 以一铆接钢桁梁桥实测车辆荷载数据为基础，建立了随机车辆荷载模型，并结合 Monte -Carlo 法提出了基于随机车辆荷载模型的钢桁梁桥疲劳可靠性分析方法。

(2) 针对该桥通行车辆的特点，以 S -N 曲线为基础建立了面向健康监测的疲劳极限状态方程,并结合随机车辆荷载模型，对疲劳应力谱进行了分析。结果表明,等效应力服从正态分布，应力循环次数服从对数正态分布或正态分布。

(3) 计算了桥梁构件随运营时间的疲劳可靠性变化，并分析了不同因素对构件疲劳可靠性的影响。结果表明,随着运营时间的增加，疲劳可靠指标逐渐变小，在运营初期，疲劳可靠指标变化较快，后期趋于平稳。车辆荷载的增大和荷载效应变异性的增加都会对构件疲劳寿命产生较大影响，当车辆荷载增长率增加到5%时，构件疲劳寿命从141年减小到44年；当等效应力的变异性从0.1增加到0.5时，疲劳寿命从198年减小到61年。

(4) 将静力分析法识别的钢桁梁桥重要构件的失效作为桥梁结构的失效，结合β约界法可快速确定结构失效模式，与单个构件的疲劳寿命相比，系统疲劳寿命偏低，但更为合理。

本文建立的基于实测车辆荷载的钢桁梁桥疲劳可靠性评估方法能充分利用长期监测数据对结构疲劳进行评估，采用β约界法和静力分析法可较为快速地计算钢桁梁桥系统疲劳可靠指标，但除车辆荷载外，车辆的运行速度和轨道不平顺性等都对疲劳应力有一定影响，有待进一步研究。