纳米流体在伸/缩楔体上的MHD流动数值研究
2020-05-22许晓勤陈淑梅林绍义
许晓勤,陈淑梅,林绍义
(1.福建船政交通职业学院 汽车运用工程系,福州 350007;2.福州大学 机械工程及自动化学院,福州 350116)
1 引 言
由于导热系数低,传统的传热流体如水、乙二醇和机油等传热性能一般,而金属的导热系数是这些流体的三倍[1]。Choi等[2]首次提出纳米流体的概念,即由尺寸小于100 nm的固体颗粒(通常由金属或金属氧化物制成)分散在基液中形成,研究发现,将体积分数为1%的纳米颗粒添加到常规流体中,会使流体的热导率增加约两倍。引起纳米流体热导率异常增大的因素很多,Buongiorno[3]经过实验研究发现,在层流情况下,布朗扩散和热泳是纳米颗粒/基液滑移机制中两种最重要的影响因素;之后,结合布朗扩散和热泳的影响,建立了纳米流体输运现象的通用两组分非均质平衡模型。纳米流体在许多工业领域、核反应堆、运输、电子、生物医学和食品中都得到广泛应用。
磁性纳米流体是含有基液和磁性纳米颗粒的磁性胶体悬浮液,磁流体(MHD)磁场参数是控制冷却速度和产品质量的关键参数之一[4]。在实际应用中,纳米颗粒由于粒度小,表面原子比例、比表面积及表面能大,处于能量不稳定状态[5],极易产生凝并和团聚现象,形成二次粒子,粒径变大,使纳米颗粒原有特性减弱或失去,因此需要在制备和保存中防止粒子团聚。目前,磁性纳米流体常见的制备方法主要有化学共沉淀法、溶胶-凝胶法、水热法、 热分解法和微乳液法等[6]。对纳米颗粒进行表面改性也是避免纳米颗粒在储存以及使用过程中发生团聚现象非常有效的方法之一[7]。
在拉伸/收缩表面上的流体流动现象广泛存在于聚合物工艺、薄膜/片材的冷却或加热、输送带、圆筒或金属板加工等场合。作为流体动力学和传热领域的一个重要部分,绕楔流动受到众多学者的关注[8]。Falkner等[9]首次分析了绕楔稳态层流现象,提出了著名的Falkner-Skan方程来描述楔体上的流动。Hartree[10]随后给出了传统楔形问题的数值迭代求解方案,提高了求解的精度。Postelnicu等[11]研究了幂律流体在变自由流下通过可渗透拉伸楔体的二维稳态层流边界层流动,发现当楔体运动方向与自由流方向相反时存在双解,并证明了下支解(第二个解)是不稳定的,而上支解(第一个解)是稳定的。Salem等[1]探讨了在磁场和粘性耗散作用下,铜-水纳米流体在可渗透楔体表面的流动和传热现象;发现当速度比参数λ为某些负值时,速度场和温度分布存在双重相似解。
本文旨在研究纳米流体在拉伸/收缩楔体上的磁流体流动与传热传质现象。在将控制偏微分方程简化为一组常微分方程后,利用打靶法得到数值解。详细讨论了各控制参数对无量纲速度、温度、浓度、表面摩擦系数、局部Nusselt数和局部Sherwood数的影响。
2 数学模型
考虑纳米流体通过拉伸/收缩楔体的稳态二维磁流体流动问题,坐标系如图1所示。x轴与楔体表面的流体流动方向平行,y轴与楔体垂直。楔体的倾斜角Ω=βπ,其中β是Hartree压力梯度参数;自由流的速度ue(x)=U∞xm,其中m和U∞是常数且为正;拉伸/收缩楔体速度uw(x)=Uwxm,拉伸时Uw>0,收缩时Uw<0。沿y方向施加可变磁场强度B(x)=B0x(m -1)/2,其中B0为常数。注意0≤m≤1,m=0时成为固定平板上的边界层流动即Blasius问题,m=1时成为无限长壁面上的驻点流问题。
为便于求解分析,忽略影响较小的因素,作如下假设,(1) 纳米流体为牛顿不可压缩流体; (2) 纳米颗粒具有统一的形状和尺寸; (3) 纳米流体为悬浮稳定和化学稳定流体; (4) 纳米流体基液和颗粒之间处于热平衡状态,且无相对滑移; (5) 感应磁场与所施加的磁场相比较小,可忽略; (6) 楔体表面均匀,仅沿x方向拉伸或收缩,无其他变形。
基于上述假设,在Navier-Stokes方程的基础上,纳米流体绕楔体流动动量方程采用Falkner-Skan方程,能量及浓度方程采用Buongiorno模型,建立控制方程如下。


图1 物理模型和坐标系
Fig.1 Physical model and coordinate system
(1)
(2)
(3)
(4)
边界条件如下。
y=0∶u=uw(x),v=vw,T=Tw
(5)
y→∞∶u=ue(x),T=T∞,C=C∞
(6)
式中u和v分别是沿着x轴和y轴方向的速度分量;T和C分别是纳米流体温度和纳米颗粒浓度;υ是运动粘度;ρ是流体密度;σ是电导率;α是热扩散率;τ=(ρc)p/(ρc)f是纳米颗粒的热容与基液的热容之比;DB和DT分别是布朗扩散系数和热泳扩散系数;Tw和Cw分别是楔体表面温度和纳米颗粒浓度;T∞和C∞分别是环境温度和纳米颗粒浓度;vw是质量流速,抽吸时vw<0,喷注时vw>0,而vw=0表示表面不可渗透。
引入相似变量:
(7)
式中Ψ(x,y)是流函数。
方程(1~4)简化为
f‴+ff″+β(1-f′2)+M2(1-f′)=0
(8)
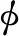
(9)
(10)
边界条件(5,6)转化为
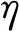
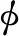
(11)
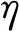
(12)
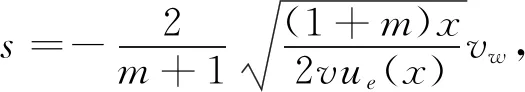
(13)
局部表面摩擦系数Cf x、局部Nusselt数Nux和局部Sherwood数Shx表达式如下。
(14)
式中 Rex=uex/υ为局部Reynold数。
3 数值方法
常微分方程(8~10)及边界条件(11,12)构成了两点边值问题,可采用打靶法结合四阶五常龙格库塔迭代方案进行数值求解。为了验证该数值迭代方法的准确性,当β=1,s=M=0时,求解λ取不同值时的f″(0),发现与其他文献结果吻合良好,结果列入表1。
4 结果讨论
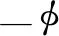
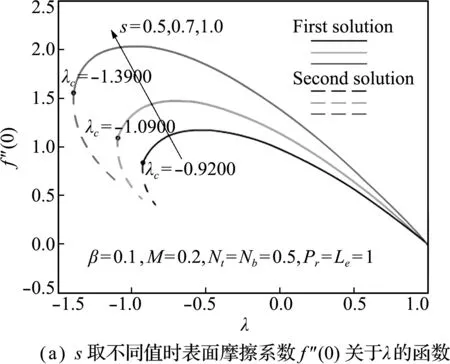
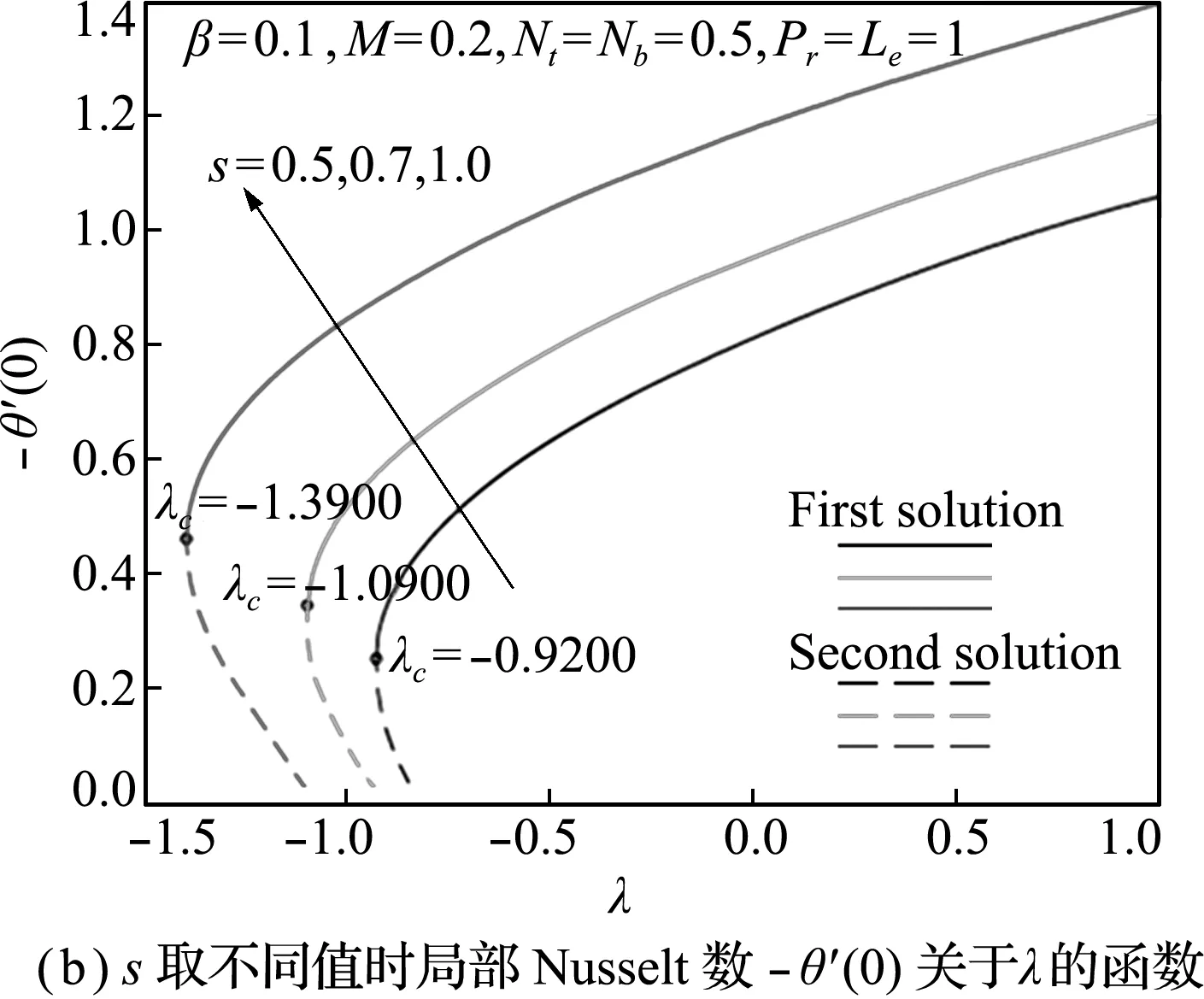
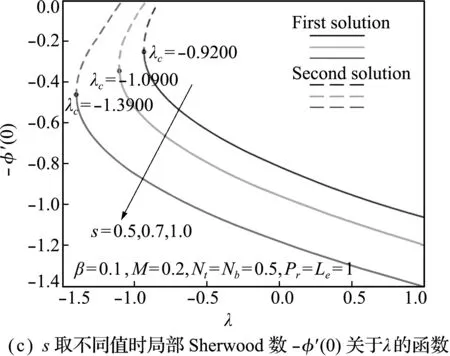
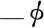
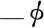
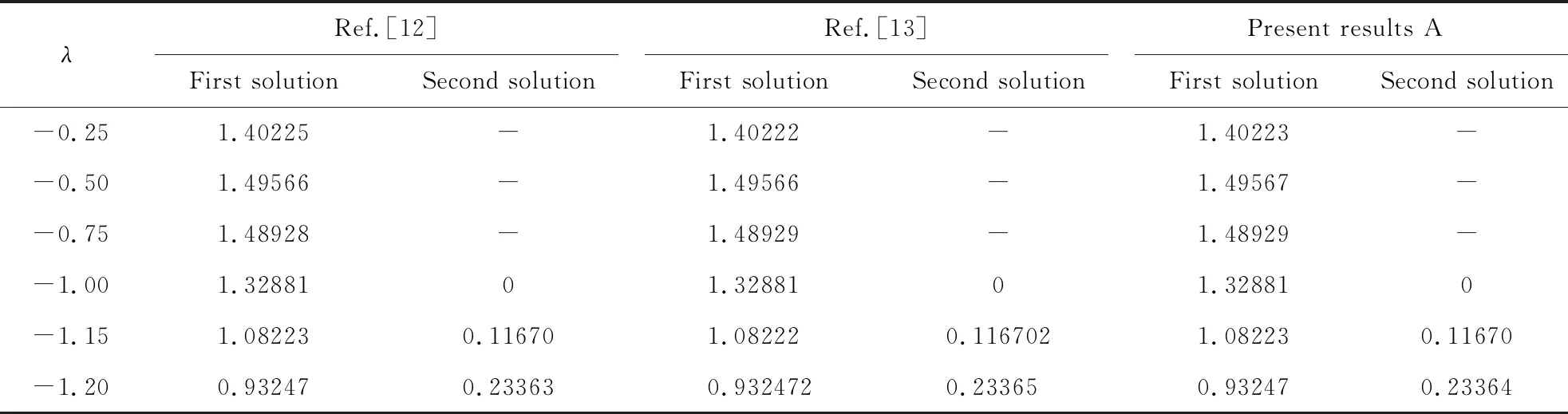
表1 λ取不同值时f ″(0)与文献结果的比较(β=1,s =M=0)Tab.1 Comparison of f ″(0) for various values of λ with references when β=1, s =M=0
图3描述了不同参数(λ,β和M)对速度轮廓的影响(Nt=Nb=0.5,Pr=Le=s=1),考虑了拉伸(λ>0)和收缩(λ<0)两种情况。可以看出,在拉伸情况下解是唯一的(只有第一个解),而在收缩情况下存在双解(有第一个解和第二个解),与 图2 结果相符。而且,第一个解的边界层厚度比第二个解的边界层厚度薄,即能更快进入稳定状态。所有曲线均满足无穷远处边界条件(f′(∞)=1),进一步验证了数值仿真结果的准确性。
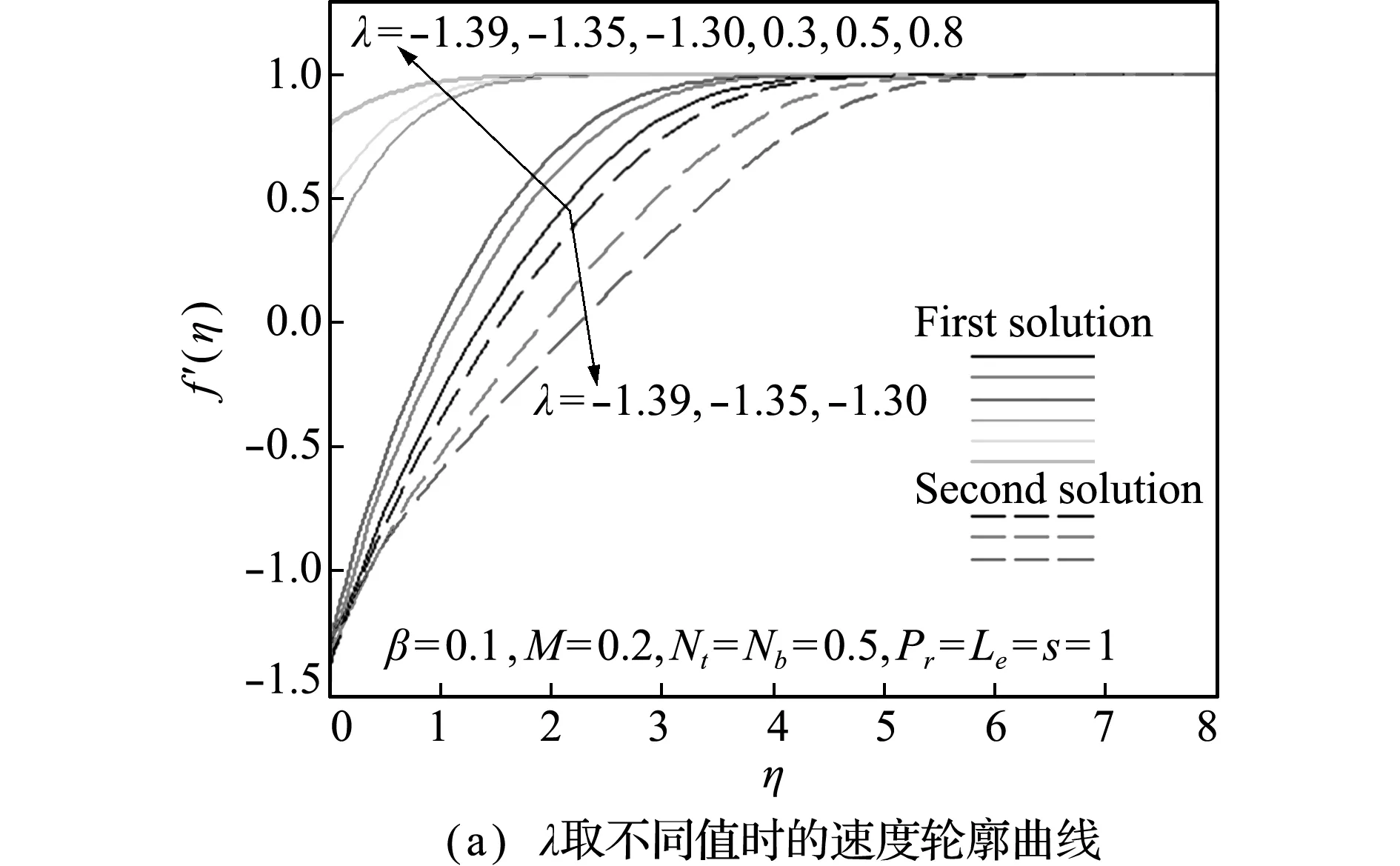

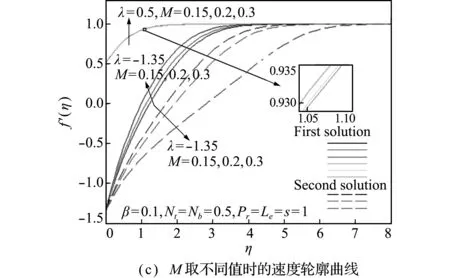
图3 不同参数(λ,β和M)对速度轮廓的影响
Fig.3 Effects of different parameters (λ,βandM) on the velocity profiles
可以看出,三个参数(λ,β和M)对速度轮廓的影响类似,在第一个解中,速度随任何一个参数的增大而增大,而在第二个解中情况恰好相反,这与Awaludin等[12]给出的结果相符。三个参数对第二个解的影响明显大于对第一个解的影响;拉伸情况下β和M对速度的影响较小,如图3(b,c)所示。
不同参数(λ,β,M,Nt,Nb和Le)对温度分布的影响如图4所示。对于每个特定的参数,拉伸情况下的温度均比收缩情况下低,且受β和M影响不大。另外,在收缩情况下,第一个解更快接近无穷远处的边界条件(θ(∞)=0),即第一个解的边界层厚度小于第二个解,显示出第一个解的稳定特性。参数(λ,β和M)对温度的影响类似,且变化趋势与速度正好相反,如图4(a~c)所示。即在第一个解中,温度随参数(λ,β和M)的增大而减小;在第二个解中,温度随参数(λ,β和M)的增大而增大。
参数(Nt,Nb和Le)对温度分布的影响如图4(d~f)所示。从图4(d,f)可以看出,对于任何一个解,温度及其边界层厚度均随Nt或Le的增大而增大。而布朗运动参数Nb对温度分布几乎没有影响(如图4(e)所示,放大图曲线显示的误差属于数值迭代误差)。与文献[18]的结果一致。
参数λ,β和M对浓度分布的影响类似,如图5(a~c)所示。与速度轮廓曲线类似,三个参数对第二个解的影响明显大于第一个解;且拉伸情况下,参数β和M对浓度分布的影响很小。
参数Nt和Nb对浓度分布曲线的影响相反,而参数Le和Nb对浓度分布曲线的影响类似,如图5(d~f)所示。
在楔体拉伸情况下,抽吸/喷注参数s和磁场参数M对表面摩擦系数、局部Nusselt数和局部Sherwood数的影响如图6所示(β=0.1,Nb=Nt=λ=0.5,Pr=Le=1)。表面摩擦系数、局部Nusselt数和局部Sherwood数的绝对值均随喷注强度的增大而减小,随抽吸强度的增大而增大,即喷注增大了流速,降低了传热速率和浓度扩散速率,而抽吸的效果与之相反,与图2的结果一致。
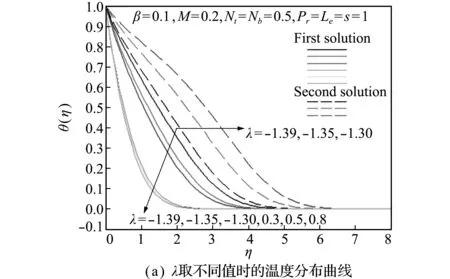
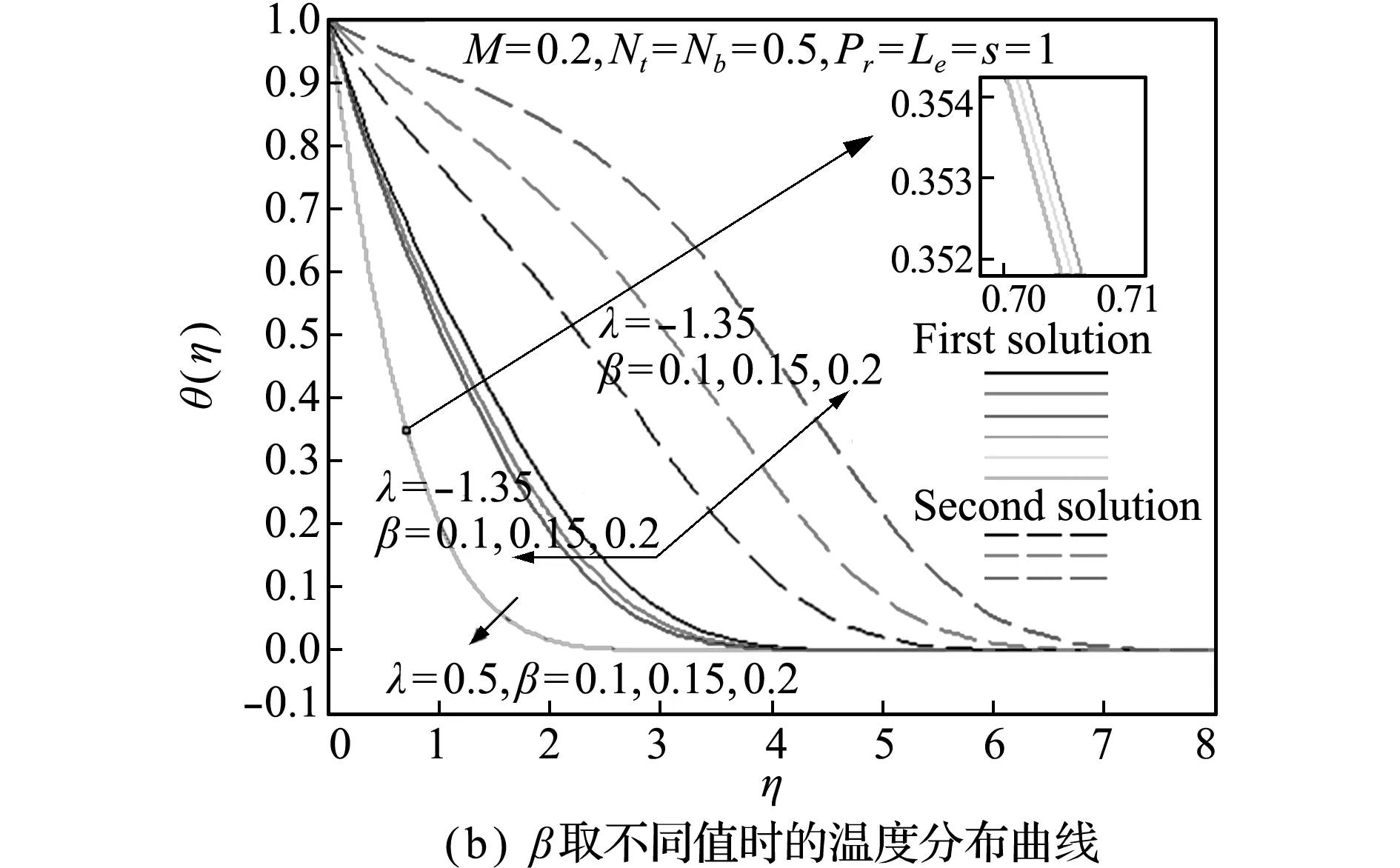
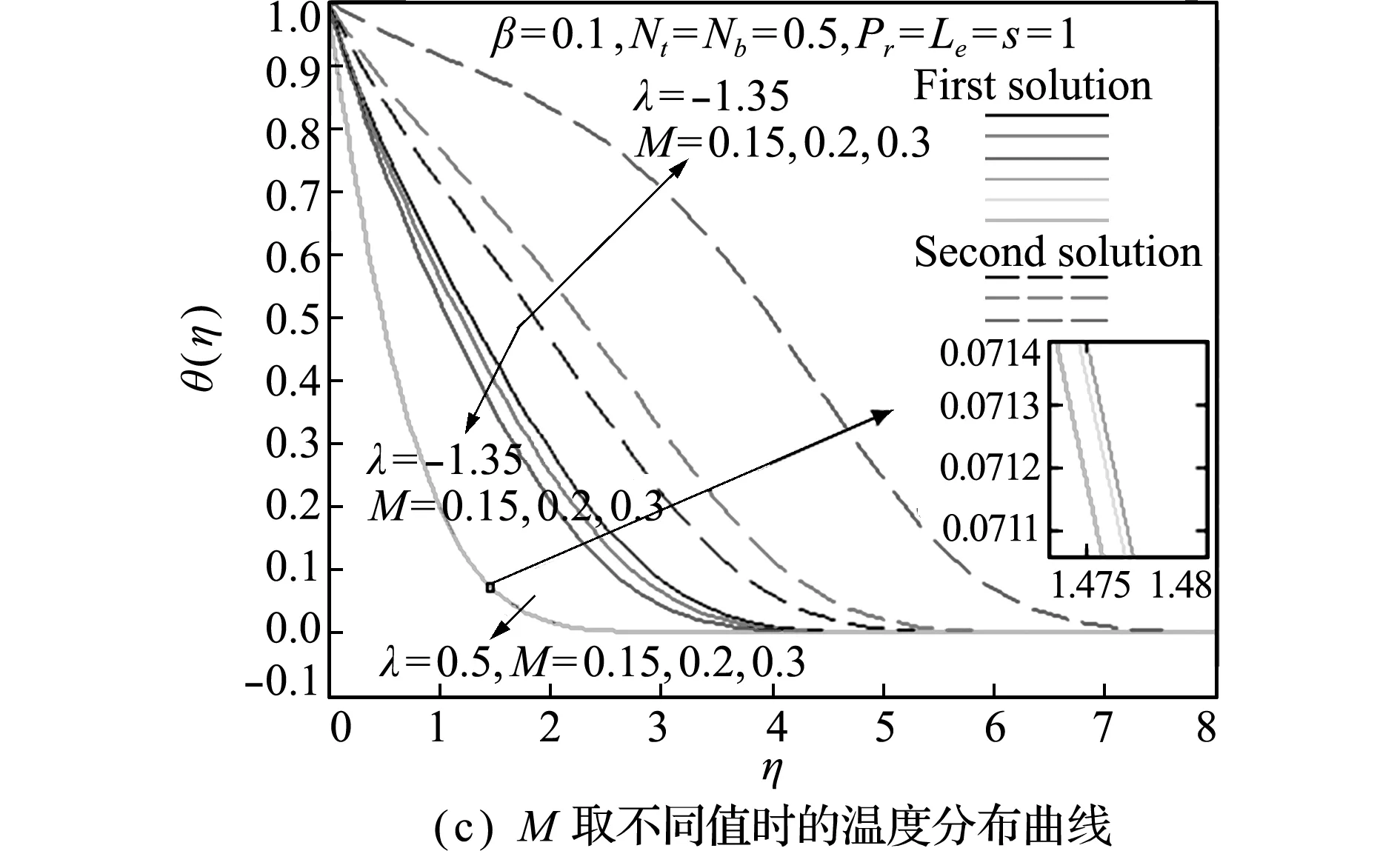

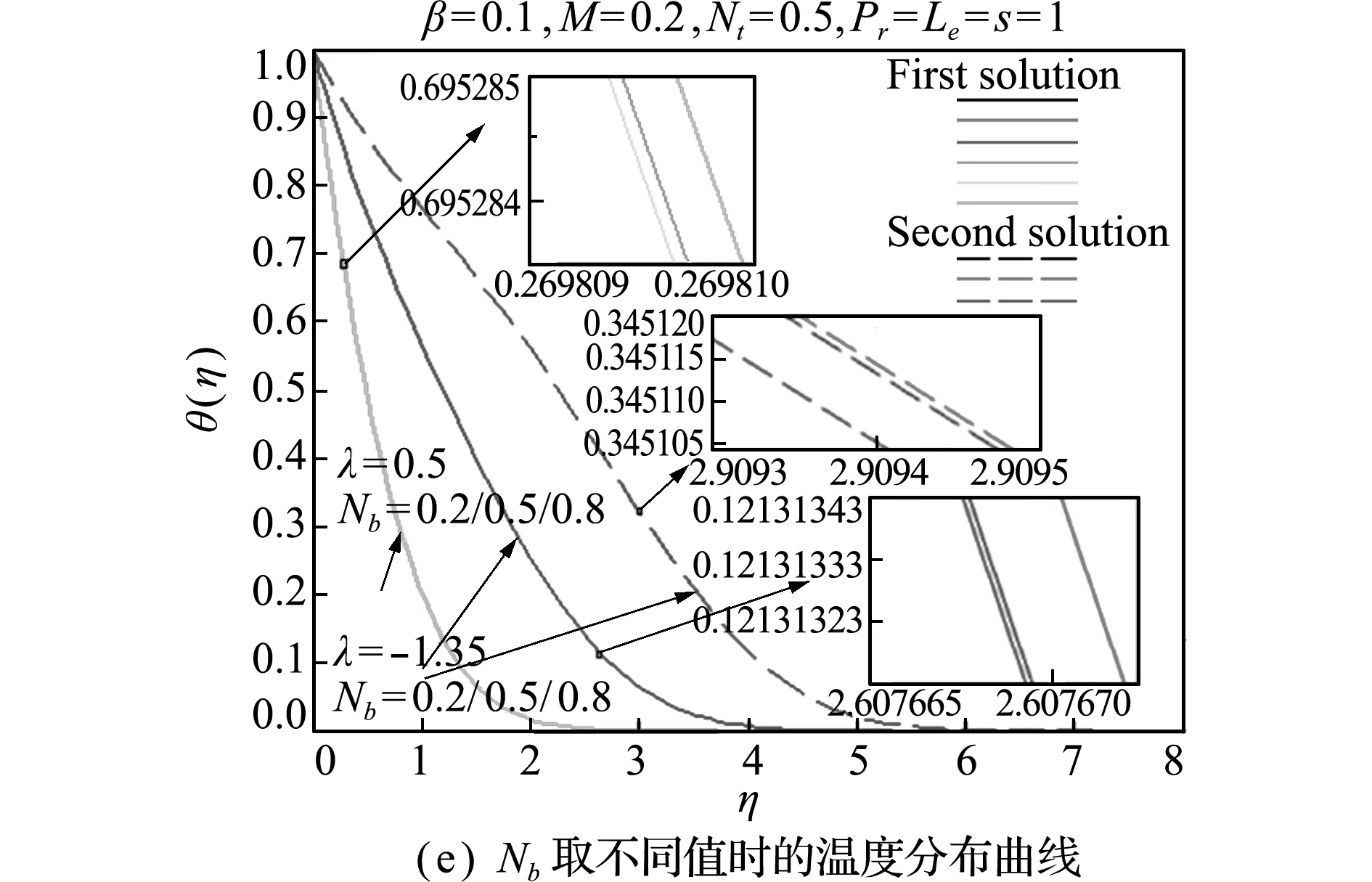
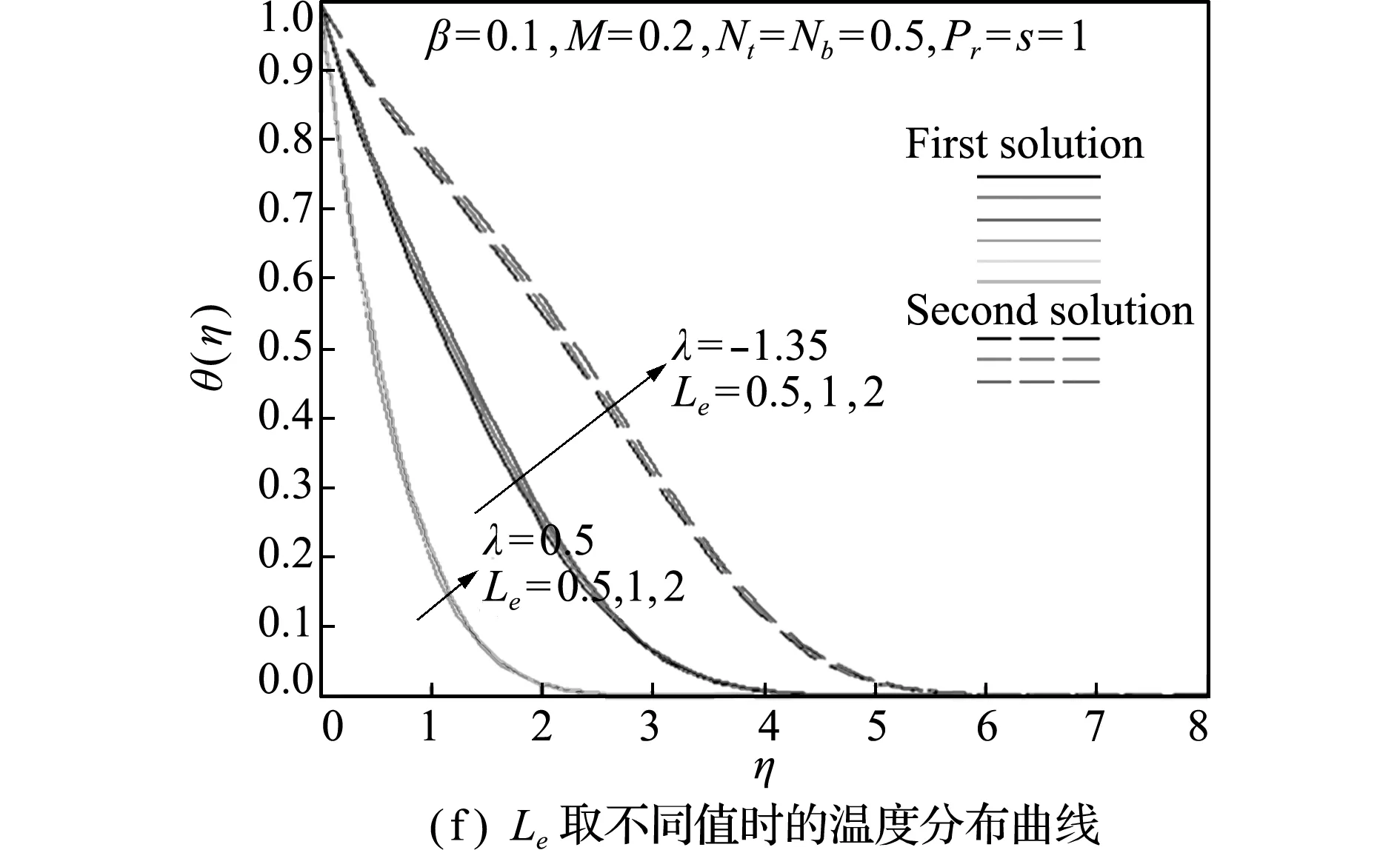
图4 不同参数(λ,β,M,Nt,Nb和Le)对温度分布的影响
Fig.4 Effects of different parameters (λ,β,M,Nt,NbandLe) on the temperature distributions
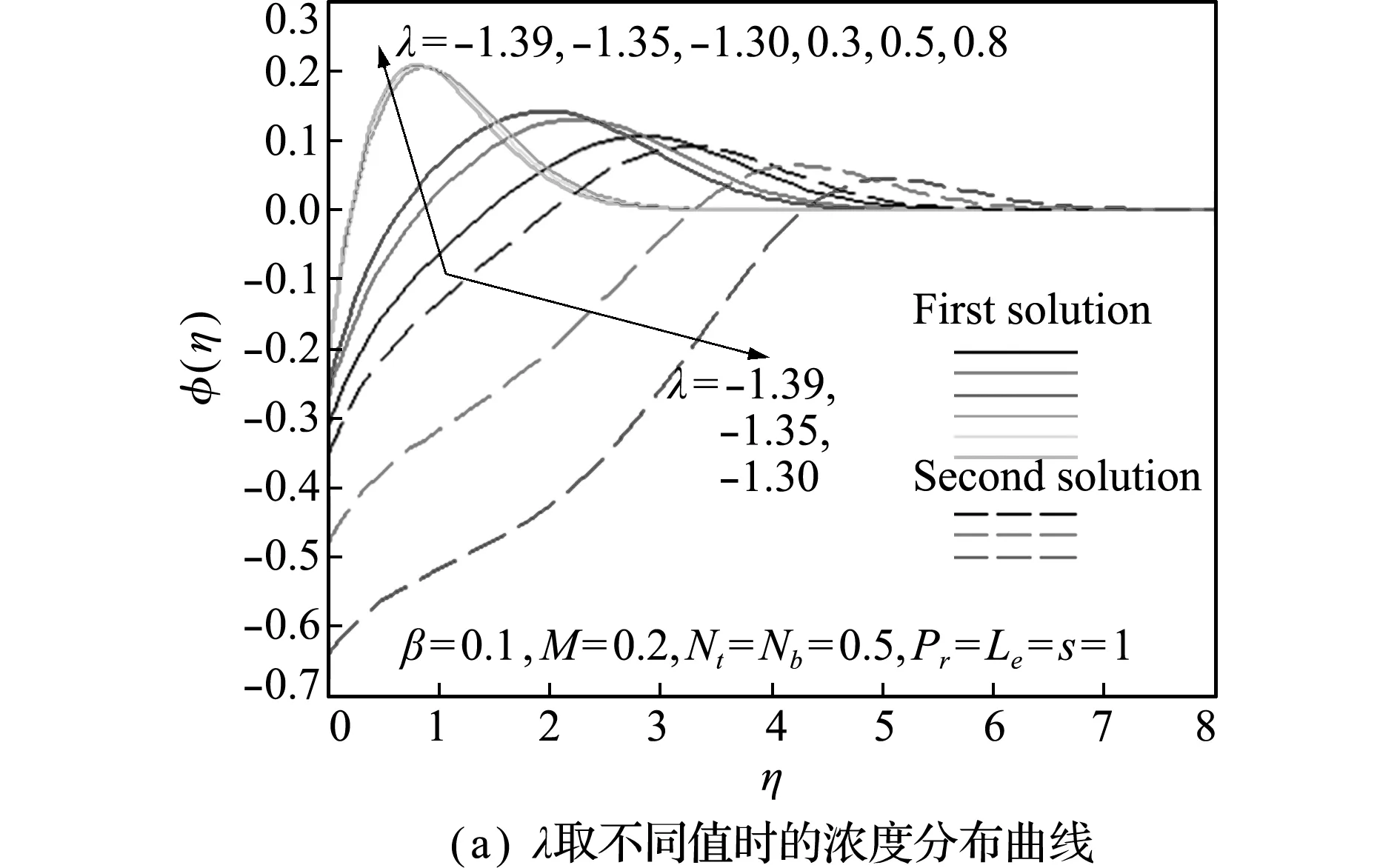
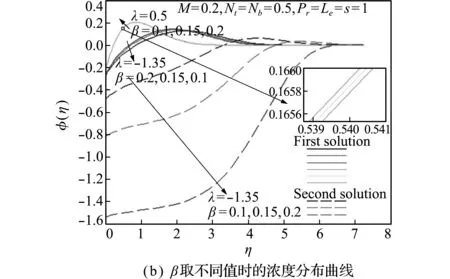
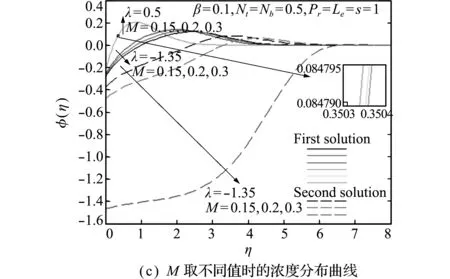
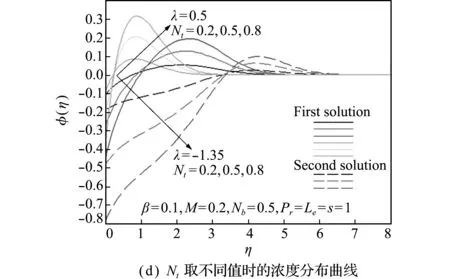
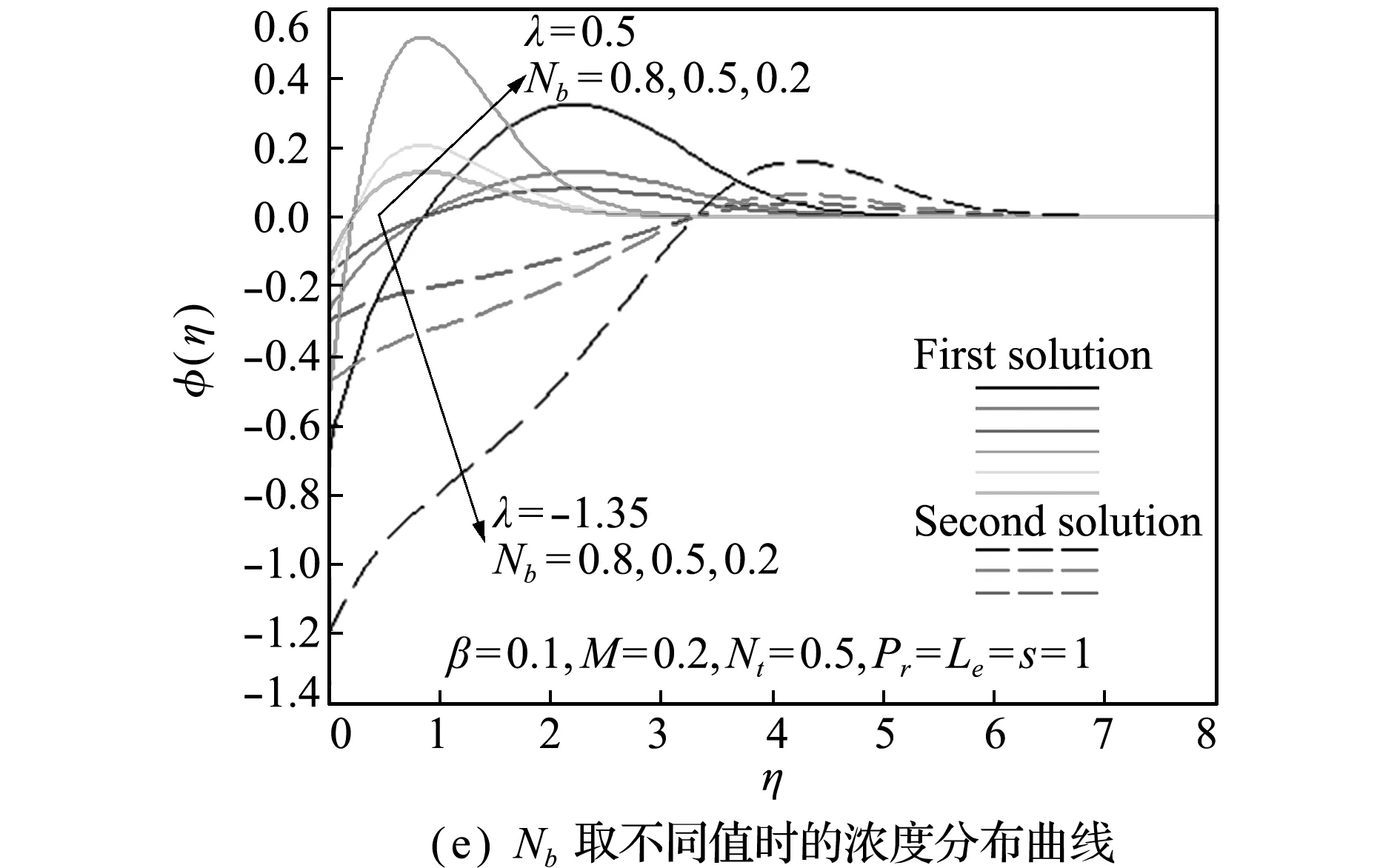

图5 不同参数(λ,β,M,Nt,Nb和Le)对浓度分布的影响
Fig.5 Effects of different parameters (λ,β,M,Nt,NbandLe) on the concentration distributions
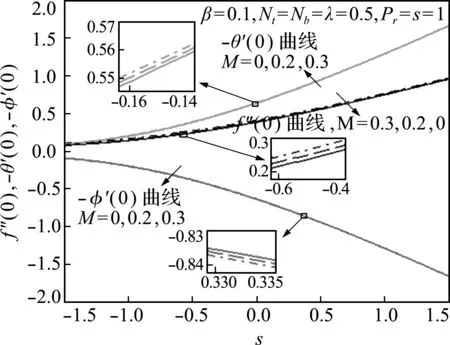
图6 表面摩擦系数、局部Nusselt数和Sherwood数与s的关系曲线
Fig.6 Plots of the skin friction coefficient,the local Nusselt number and the Sherwood number versuss
5 结 论
本文分析了纳米流体在拉伸/收缩楔体上的磁流体流动与传热传质现象,考虑了抽吸/喷注参数的影响。采用打靶法进行数值求解,得出各控制参数对流场、温度场和浓度场的影响规律,主要结论如下。
(1) 楔体在拉伸情况下只有唯一解,理论上不会出现边界层分离现象。
(2) 楔体在一定的收缩强度范围内存在双解, 意味着楔体收缩时层流边界层在壁面处可能会出现分离;壁面抽吸可使边界层分离推迟。
(3) 在楔体拉伸情况下,喷注增大了流速,降低了传热速率和浓度扩散速率,而抽吸的效果相反。
(4) 磁场参数对表面摩擦系数的影响较大,对局部Nusselt数和局部Sherwood数的影响较小。
本文对于分析表面收缩引起的边界层分离与控制方法,研究纳米流体在楔体表面流动时,各参数对速度轮廓、温度分布和浓度分布的影响规律有一定的借鉴意义。
