加权质心算法在Wi-Fi室内定位中的应用
2020-05-19童笑宏王冠凌
童笑宏,王冠凌
(1.高端装备先进感知与智能控制教育部重点实验室,安徽 芜湖241000; 2.安徽工程大学 电气工程学院,安徽 芜湖241000)
0 引言
由于室内环境的多变性和复杂性,使得Wi-Fi信号在传播过程中波动较大,限制了传统的定位技术,如TOA、TDOA、AOA等的定位精度,同时采用硬件检测,使得成本较高.有学者提出通过离线采集和在线匹配的Wi-Fi室内定位方法[1].离线阶段,采集的RSSI值受到室内环境、物件位置等不确定因素的影响,需要对采集以后的数据进行滤波处理,消除特异值,构建新的指纹数据库;在线阶段,则进行指纹匹配,但是未对采集的数据进行滤波等预处理,数据受噪声和多径影响较大,定位精度不足、稳定性不够.也有学者提出一种在KNN算法的基础上,融合朴素贝叶斯概率算法来实现室内定位[2-5].这种改进后的算法在Wi-Fi定位上虽然提高了室内定位算法的稳定性,但是对采集的数据未具体划分类别,使得相似度较高的采样点未统一聚类,导致有效数据丢失,影响定位结果.还有学者提出四边测距定位算法[6-8].该算法对采集点位置信息加权,使得位置信息更加区域化、精确化,但得到的数据分布较为分散,匹配时速度较慢.此外有学者提出的自适应权重算法[9-13],对RSSI测距算法优化,消除不同发射功率对测距的影响,通过预估和更新锚节点和未知节点距离信息,来实现精准测距.但该算法应用在复杂的室内环境时,采集的RSSI信号有一定程度的波动,影响了定位精度.
对信号时变性研究过程中,环境因素的改变是信号波动的主要原因,基于RSSI的室内定位算法在长时间定位中为了让其保证一定的定位精度,对采集的指纹库要定期改进[14],维护和改进使得成本上升,工作量增加.本文通过改进的基于加权质心算法的Wi-Fi室内定位方法,不仅避免了人工对设备的长时间维护,而且节约了成本.
1 卡尔曼滤波
由于室内Wi-Fi定位所采集的RSSI值满足高斯分布,靠近已知AP点信号强度越高,反之越弱,但受多径效应的影响,采集的RSSI值有特异值点的存在.因此采用卡尔曼滤波算法,通过预测和更新过程消除特异值.在RSSI信号采集过程中,受室内多径效应的影响,使得采集的信号强度值波动较大.在实际定位过程中,一是要使定位结果具有实时性,一般需要3 s内计算出目标位置;二是采集设备硬件自身限制,使得采集速度有限(1 s/次);三是定位结果在突变信号中精度大幅降低.使用卡尔曼滤波能有效过滤异常值点,提高定位精度.滤波效果如图1和图2所示.
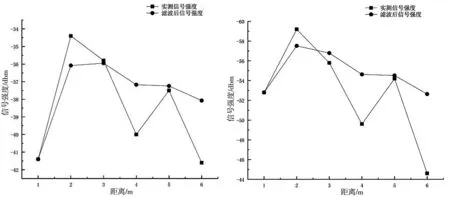
图1 第1组滤波数据 图2 第2组滤波数据
2 基于信号强度的测距模型
2.1 距离定位算法
传播中的信号强度会随距离的增加而衰减,同时,信号的强度衰减幅度也意味着距离的变化,这一规律符合距离测量的对数衰减模型.
在室内复杂环境的定位中,采集的信号会受到反射、散射、遮蔽的影响而产生很大的干扰,一般的数学模型无法描述信号变化趋势,因此,学者们广泛采用对数正态分布处理接收信号的强度,并进一步使用对数正态阴影模型来刻画信号强度随距离的变化[15],其数学表达式为
(1)
其中:P0(d)和Pr(d0)分别为接收在距离信号源为d和d0处接收到的信号强度;η为路径损耗参数;Xσ为服从正态分布的随机变量.本文通过多次测量数据实验验证,η值和Xσ值在此测试环境中分别为2.0和2.6,然后以锚节点为圆心,对数路径损耗模型计算的距离为半径,计算组成的三角形的质心坐标,即为待测点坐标.
2.2 数学模型建立
以锚节点作为球心,分别绘制数学模型的三维图如图3、三维俯视图如图4、和二维截面平面图如图5.
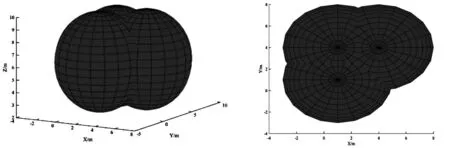
图3 数学模型三维图 图4 数学模型俯视图

图5 数学模型二维截面图
2.3 基于RSSI质心算法
利用网络连通性以锚节点为圆心、依据距离模型计算的待测点与锚节点距离为半径画圆,得到三圆相交的可定位区域,计算待测点坐标就是计算三角形的质心坐标,三维数学模型建立如图3,二维平面模型如图6.该算法操作简单,同时,定位精度会受多因素的影响,如锚节点位置和分布越离散,定位精度就越低,反之,定位精度就越高.由此,该算法导致的定位精度不高是因为等同化AP点作用,弱化AP点到待测 点距离对计算待测点坐标的功能.例如N个锚节点组成公共区域(图7),从而估算待测点的坐标(X,Y)为
(2)

图6 三圆定位示意图 图7 三角形区域
2.4 加权质心算法
该算法利用的权重值[16-20]是AP点和未知节点的距离的倒数,待测点坐标(X,Y)可根据AP点坐标(x1,y1),(x2,y2),……,(xi,yi)求得,即:
(3)
其中:wi为第i点的权值;(xi,yi)为第i个已知点到待测点间的距离.xi越大,wi就越小,反之wi则越大.
已知3个圆相交可以得到三个交点,但是通常情况下是得到一片待定位区域,本文采用3个圆相交,计算交点组成的三角形的质心坐标.依据测量平差原理,提高定位精度可以增加多余观测量,但多余观测量越多,计算就越加复杂.因此改进的RSSI室内加权质心定位算法使用3个圆相交来计算待测点坐标计算过程更简易.
3 改进的RSSI室内加权质心定位算法
3.1 算法原理
本文改进的定位算法思想在于,当3个圆相交时会得到一个待定位区域(图8),相交的3个交点E、F、G组成一个三角形(图7),MEFG(XEFG,YEFG)为该三角形的质心坐标,P(Xp,Yp)为待测点坐标.
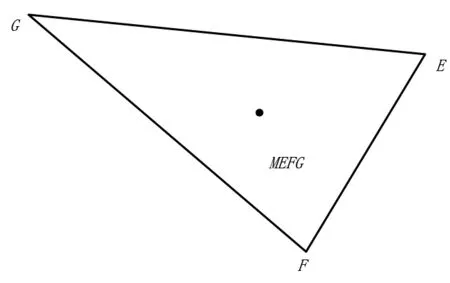
图8 可定位三角形区域
使用对数路径损耗模型公式计算节点A到交点E的距离、节点B到交点F的距离、节点C到交点E的距离分别为dA、dB、dc,并分别以距离为半径,节点A、B、C为圆心画圆,得到待定位区域,交点分别为E、F、G.交点的计算方法为E、F、G交点E(XE,YE)的计算方法为
(4)
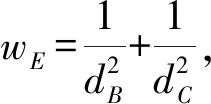
(5)
由此解出的坐标(XEFG,YEFG)即为三角形质心坐标.
本文改进的定位算法需要对锚节点位置进行初始设定,再采集信号点进行室内定位,避免可定位区域过大或过小造成的定位精度的降低.无线传感器网络的普及,让Wi-Fi有很高的覆盖率,因此利用Wi-Fi信号来实现室内精确定位更加便捷.
4 算法流程
本文通过手机采集接收的Wi-Fi信号值,然后通过卡尔曼滤波算法消除特异值,增加定位精确度,通过对滤波后的数据进行判断是否达到阀门值(经过多次实验证明,阀门值设定为-60 dbm),对达到阀门值数据利用公式(1)计算距离,当三圆相交有且仅有三个交点时,按照公式(4)和公式(5)计算三角形质心坐标.算法流程如图9所示.
算法步骤如下:
1)所设定的AP点周期性地向周围发射附有无线锚节点自身的位置信息和ID号的消息包.
2)利用卡尔曼滤波过滤接收的异常Wi-Fi信号强度点,再利用对数路径损耗模型通过信号强度计算距离值.
3)当未知节点接收消息包的时间达到阀门值的时候,停止接收消息包.
4)对达到阈值的数据继续利用对数路径损耗模型把接收到的RSSI信息转化为距离值.
5)取步骤1)中设定AP点的坐标值和步骤4)中选出的距离值,通过公式(4)计算出所求交点的坐标.
6)计算步骤4)和步骤5)中3个交点的坐标值,通过公式(5)计算三角形的质心坐标,即待测点P的坐标值.

图9 算法流程图
5 实验设计
本文实验地点在控制工程实验室.实验室三个顶角设置3个采用相同普通型号路由器Tengda-AC6发射的Wi-Fi接入点(图10),节点坐标分别为(0,0,4),(6.6,0,4)和(6.6,6.6,4),单位为m.

图10 实验环境
采集点坐标如图11所示.

图11 采集点坐标图
6 实验结果分析
1)在室内部署3个相同类型的无线路由器,在实验区域内建立独立平面坐标系.利用标尺在建立的坐标系下测量无线路由器和待测点的坐标值.
2)使用手机下载的WIFI信号强度检测器进行信号采集,信号采集时需采集两组数据,对数损耗模型中的P0(d)是1.085 0 m处的信号强度.构建出对数路径损耗模型:
(6)
另一组数据是在8个检核点上分别使用相同型号手机进行采集信号.用于检核点定位验证.
3)利用改进的RSSI室内加权质心定位算法将移动端接收到的信号强度进行计算,得到检核点的估算坐标(xEFG,yEFG).
4)以估算坐标值与真实坐标的距离值作为精度评价依据,同时,采取e值(X和Y方向误差的平方和后开根号)乘以100%为定位精度百分比.经计算,e值在95%左右,即定位精度提高95%左右.
(7)
其中:(xEFG,yEFG)为检核点的估算坐标值,(XEFG,YEFG)表示待测点的实际坐标值.测试点定位误差比较如表1,算法误差比较如表2所示.

表1 测试点定位误差比较 单位:m

表2 算法误差比较 单位:m
由上表2可以看出,加权质心算法的误差相较于基于RSSI的测距算法误差和基于RSSI的质心算法误差有相当大的优化,基于RSSI的测距算法的最大误差是1.206 m,最小误差是0.752 1 m,平均误差是1.001 2 m;基于RSSI的质心算法的最大误差是1.475 6 m,最小误差是0.895 4 m,平均误差是1.200 9 m;本文改进的加权质心算法的最大误差是1.088 2 m,最小误差是0.735 4 m,平均误差是0.939 5 m.比较可知:0.939 5 m<1.001 2 m<1.2009 m,因此,加权质心算法满足较高的精度要求,更适合于室内多径效应造成的复杂环境的定位.从上表1对X方向和Y方向的误差分析可以看出:其X方向最大误差是0.666 0 m,X方向最小误差是0.428 0 m;Y方向最大误差是0.875 0 m,Y方向最小误差是0.564 0 m;X方向平均误差是0.528 5 m,Y方向平均误差是0.774 5 m.由表2算法误差比较可以看出,改进算法与测距算法以及质心算法分别做差再乘以百分之百后得到的八个数据点定位精度平均提高10%左右,体现了加权质心定位算法的应用具有精度高的特点.
7 结论
本文改进的定位算法在计算待测点坐标时,通过距离平方计算权值加权得到初始定位坐标,为了防止误差较大,使用信号强度二次加权,最大限度将获得的RSSI信息通过几何关系转化为待测点坐标,实验验证,改进的算法使得定位精度有一定程度的提高,有效地降低了由于室内多径效应和噪声对定位精度的影响,可以满足室内定位、无人机定位等方面的部分需要.在定位精度上,改进的定位算法,利用两次加权计算的结果作为最后定位坐标值,在与RSSI测距算法和RSSI质心算法比较中,定位精度平均提高了10%左右.
