位置指纹定位中WiFi信号特性分析及处理技术研究
2022-05-19司国雷陈君辉
邓 熠,司国雷,陈君辉,潘 游
(四川航天烽火伺服控制技术有限公司,四川 成都 611130)
1 概述
目前,随着无线网络在室内场所的普及,充分利用现有无线网络设备,以较低的技术成本和较高的位置精度实现非视距环境下定位,满足人们对于室内位置信息的需要,是目前向定位技术的研究热点,故基于无线网络的室内定位技术孕育而生。根据不同无线网络类型,室内定位技术分为辅助GPS 室内定位(AGPS)、超声波室内定位、红外线室内定位、蓝牙室内定位、超宽带室内定位、ZigBee室内定位及WiFi室内定位[5-8]。各类室内定位技术在定位精度、网络规模、系统成本及普适性等方面的优劣性,如表1所示。通过对表1中所展示的各类室内定位技术性能指标分析可知,以WiFi网络为基础的室内定位技术在定位精度、网络规模、系统成本及普适性方面存在不可比拟的优势。

表1 室内定位技术特点对比Tab.1 Comparison of Indoor Location Technologies
WiFi 室内定位技术利用信号强度值(RSSI)随着与WiFi 信号接入端(AP)距离的增大而不断衰减的原理,形成了基于传播损耗模型法和基于位置指纹法两种不同的室内定位方式。其中,位置指纹法利用采样数据能够真实反映定位场景的WiFi信号强度及其物理位置这一特点,在无需掌握室内障碍物衰减参数的情况下,提前构建合适的位置指纹数据库,而构建用位置匹配算法对输入数据进行搜索,完成对定位场景中终端位置的实时定位,具备较高的场景适用性及定位精度。位置指纹定位方法分为离线数据采集,搭建位置指纹数据库阶段和在线定位搜索阶段[9-10]。通过文献[4]所述的定位原理可知,在采集信号强度值时,由于信号自身的传播特性存在由多径传播、非视距传播以及随机干扰等诸多因素产生的干扰及误差,会严重影响信号强度值采集工作。而离线采集数据的稳定性和可靠性,是保证系统定位精度的重要因素[4]。因此,为提高离线采集信号强度值数据的稳定性及可靠性,对WiFi信号的固有统计特性进行分析,搭建合适的滤波算法以削弱信号传播中出现的干扰和误差,是保证位置指纹定位法在室内定位中保持高效性和准确性的必要手段。故而开展WiFi 信号的预处理技术研究具有重要的意义。
2 WiFi信号的分布规律及统计特性
在以位置指纹为基础的WiFi室内定位技术中,系统的定位精度受构建位置指纹数据库时,采集数据的稳定性和精确性的影响。信号源与移动终端的相对高度、水平距离及方位角,将直接影响采集数据的稳定性和精确性[11]。为提高采集数据的稳定性和精确性,必须在具体的信号传播环境中,针对WiFi信号的分布规律及统计特性开展研究,并从中提取出符合当前向环境的WiFi信号强度值分布特征,找出合适的数据预处理方法,削弱信号因外部不明因素而产生误差干扰,为后向续的定位工作提供充足理论基础。
为了研究WiFi信号在室内分布的规律,需在室内针对某个信号源不同距离和不同方位角的接收信号强度值进行连续观察与研究。而已有文献[1-3]表明,在短距离内(1~3)m,由于距离信号源较近,其信号强度值较强,不易受到外界环境干扰。而当距离在(3~6)m 时,这个区域内接收到的信号强度值也比较强。但由于距离不远不经,故而会出现些许不明显的随机干扰,属于中间区域。当信号源与接收端的距离超过6m 时,此时信号强度值开始明显减弱,同时容易受到室内环境的影响,信号强度值出现明显的波动,使得采集得到的信号强度值极不稳定[1-3]。故这里重点研究处于中间区域(接收端与信号源相距(3~6)m的信号接收端,在不同方位角等距离处的单一信号源的信号强度值接收情况。
(1)不同方位角等距离处的WiFi信号强度值分布规律
这里设计的WiFi信号强度值采集实验分布实验处于大小为(10×6)m 的房间内进行,WiFi信号由TPLINK 450m 系列全向路由器产生,移动终端为DELL Inspiron 14 系列笔记本电脑,信号采集软件为自行编写的软件,信号总采集次数为300次,采集周期为2s,路由器安装位置处于实验房间正中心,且其安装垂直高度与移动终端处于同一水平面,具体实验内部环境,如图1所示。

图1 实验环境布置Fig.1 Layout of Experimental Environment
在定位系统的使用中,待定位对象会分散在定位空间的任意位置,由WiFi信号的多径传播特性可知,当移动终端处于相同位置但方位角不同时,其接收到的信号强度值也具有一定的随机性。同时由于两者的方位角不同,将进一步增加WiFi信号因多径传播而产生的随机误差,使得WiFi信号强度值在数值分布上出现无规律性。为弄清不同方位角对WiFi信号强度值带来的影响,搭建如下实验平台,如图2(a)所示。而后定义θ4=-90°为前向、θ2=90°为后向、θ1=0°为左向及θ3=180°为右向作为测试方位角,利用自行编写的信号采集软件进行数据采集并给出不同方位角下等距离WiFi信号分布及直方图,如图2(b)、图3所示。

图2 不同方位角等距离WiFi信号实验(移动终端与信号源间距:4m,位于同一水平面)Fig.2 WiFi Signal Experimen(tMobile Eerminal and Signal Source Distance:4m,Located on The Same Horizontal Plane)
此次实验中,所有移动终端均匀分布在以信号源为中心的四个方位角上,该方位角集合θ={θ1,θ2,θ3,θ4},如图2(a)所示。由于所使用的信号源为TPLINK 450m 系列的全向路由器,则在任意方位角上各移动终端接收到信号的理论强度值应趋于接近或相似。但在实际实验中,位于方位角集合θ上各移动终端接收到的WiFi信号强度值分布和概率分布却并非相似,如图2(b)及图3所示。图2(b)表明,即便采用了全向无线路由器,由于信号间存在相互干扰、衍射、反射等现象,无法使得信号在空间中理想的状态进行传递。另外,还发现各方位角的信号强度值分布极不稳定,使分布曲线出现骤增或骤降现象。进一步计算各方位角信号强度值的均值μ,如表2所示。之后遍历各WiFi信号集中所有信号强度值并与均值μ求差,将其结果记为δ,并提取结果中较大的值记为δ’。通过对比δ’与δ的范数大小发现,各方位角的WiFi信号集中均存在使得||δ’||>>||δ||的信号强度值,如表3所示。通过深入分析可知,在信号强度值与均值μ的差值较大处,均出现信号强度值骤增或骤降现象,表明了此时信号在传播中受到的外界干扰较大,其强度值包含较大的粗大误差。出现这种现象的原因是信号在传递过程中因互相干扰、衍射和反射,使信号各分量场到达接收端的时间不同,导致各分量按照各自的相位叠加,产生信号干扰,使得原有信号失真或出现错误,最终出现了信号强度值骤增或骤降的不稳定现象。

表2 不同方位角上WiFi信号值均值Tab.2 Means of WiFi Signals in Different Azimuth Directions
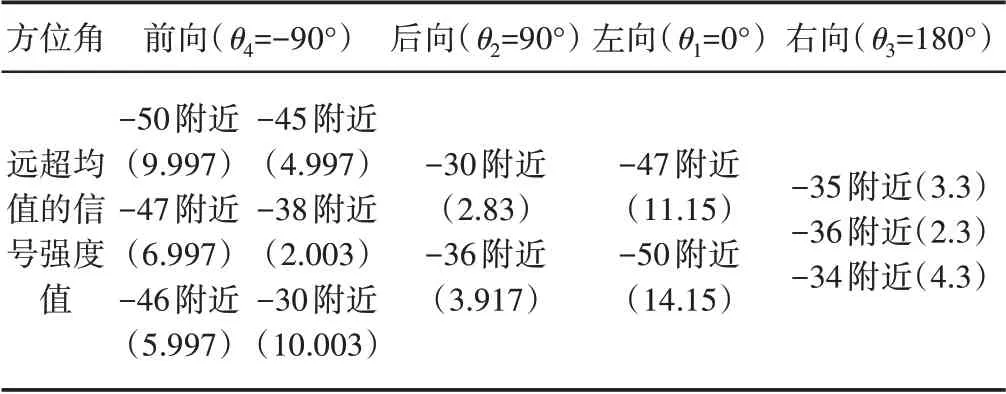
表3 各个方位角上远超均值的信号强度值(括号内表示δ’的绝对值)Tab.3 Signal Intensity Values Exceeding the Mean at Each Azimuth(Absolute Value of Deviation From the Mean in Parentheses)

图3 不同方位角等距离WiFi信号强度值概率分布Fig.3 Probability Distribution of WiFi Signal Intensity Value
(2)不同方位角等距离处的WiFi信号强度值概率特性
在分析了不同方位角等距离处的WiFi信号强度值分布规律后,为进一步明确不同方位角等距离处WiFi信号强度值的固有特征属性,以选择合适的滤波算法对其进行信号预处理,提升其数据的稳定性,特此开展针对WiFi信号强度值统计特性研究。
各方向角上移动终端接收到的WiFi信号强度值概率分布如图3 所示。通过观察图中的概率分布状况发现,各方位角上的WiFi信号强度值概率分布近似高斯分布。在统计学中,判断随机变量是否服从高斯分布时,将采用偏度和峰度两个指标进行衡量。偏度描述的是随机变量概率分布的不对称性,即随机变量分布的不对称程度及方向,而峰度则描述了随机变量概率分布相对于高斯分布的陡峭性和平缓性。根据图3 所示数据,利用式1 进一步计算各方位角上WiFi 信号强度概率分布的偏度和峰度,其结果,如表4所示。

表4 各方位角信号强度值的偏度与峰度Tab.4 Deviation and Kurtosis of Signal Intensity Values

式中:X—随机变量集合{x1,x2,x3,…,x}i;
μ—随机变量的均值;
σ—随机变量的标准差。
由表4可知,各方位角信号强度值的偏度均小于0,意味着各方位角的信号强度值概率分布均呈现左偏移现象,与图3所示的概率分布中,大量数据分布在右侧而导致其左侧数据出现拖尾现象相吻合。然而部分方位角的信号强度值的概率分布左偏移现象不明显(即图3(b)、图3(d)),其原因为方位角后向(θ2=90°)和方位角右向(θ3=180°)的偏度较小值,使得这两个方位角信号强度值分布的不对称性较弱,更加接近标准高斯分布。另外,位于方位角前向(θ4=-90°)、后向(θ2=90°)及左向(θ1=0°)的信号强度值概率分布形态相比于标准高斯分布形态较为陡峭,而位于方位角右向(θ3=180°)概率分布形态则较为矮小。这是由于信号强度值的概率分布形态直接受峰度值的正负直接影响,故而表4中的计算结果为方位角前向(θ4=-90°)、后向(θ2=90°)及左向(θ1=0°)的峰度值为正,而方位角右向(θ3=180°)的峰度值为负。
(3)不同方位角等距离处的WiFi信号强度值自相关性分析
WiFi信号强度值的自相关性描述了同一移动终端在相同位置(与WiFi信号发射端距离相同,方位角相同)不同时刻下,采集到的各信号强度值的相似程度。其中,自相关系数刻画了不同时刻WiFi信号强度值的相似度大小,而滞后阶数则表明,在相同信号采集条件下,重复采集一定次数后,其分布状态将趋于平稳。本次实验对WiFi信号强度值每2s采集一次,并设各方位角的信号集为Xθi={t1,…,tn,x1,…xn}(i=1,2,3,4),由表2结果可知Xθi的均值、标准差及任意时刻的协方差均为常数,与时间t无关,故可知Xθi为平稳时间序列。为明确相同距离、不同方位角下,WiFi信号强度值在不同时刻的相似程度,利用式2计算各方位角信号强度值弱相关时的自相关系数βk及滞后阶数k,并根据计算结果给出各方位角的信号强度自相关系数衰减图,如表5、图4所示。
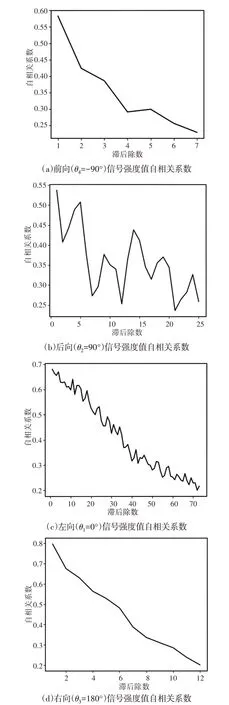
图4 不同方位角等距离WiFi信号强度值自相关系数图Fig.4 Autocorrelation Figure of WiFi Signal Intensity Value

表5 信号强度值弱相关时自相关系数及滞后阶数Tab.5 Autocorrelation and Delay Order

式中:xm—信号集中信号强度值分量;xm+k—信号集中滞后k阶的信号强度值分量;μ—信号集的均值;βk—信号集自相关系数;k—信号强度值弱相关时的滞后阶数,通常取|βk|≤0.3认为此时集合中各数据具有弱相关性。
表5所示的自相关系数βk与滞后阶数k呈对应关系,表明了在当前滞后阶数下,各信号强度值相互间的相关性。同时也表明了,每个方位角采集的数据在稳定状态下,所需的最小采集次数。即左向(θ1=0°),最小采集次数为74次,后向(θ2=90°),最小采集次数为26次,右向(θ3=180°)最小采集次数为13次,前向(θ4=-90°),最小采集次数为8次。对自相关系数的衰减结果仔细观察,发现各信号集在滞后1阶(k=1,原始信号强度值分布状态)时,各信号强度值的自相关系数βk≥0.5,表明此刻各信号强度值的自相关性处于一般相关,该结果并不理想,如图4所示。进一步观察图4,发现位于左向(θ1=0°)和后向(θ3=180°)方位角的信号强度值自相关系数的衰减曲线存在极为明显的波动。深入对其波动现象的产生机理分析可知,信号传播时,会因环境干扰、随机干扰而产生随机误差和粗大误差。由于每次信号强度值采集时间间隔较短,这就使上一次信号传播时,产生的随机误差和粗大误差不能及时得到抑制和削弱,导致其在空间中遗留部分残差并以线性增长的形式进行积累,影响下一次信号的传播状态。该过程的数学描述,如式(3)所示。

式中:xm—当前时刻接收的信号强度值;
x’m—WiFi信源信号强度值;
Δ(xm)—当前时刻信号在传播过程中产生的随机误差及粗大误差;
Δ(xm-1)—上一次信号传播过程中遗留的残差。
由式3可知,误差项Δ(xm)及Δ(xm-1)在信号传播中与当前时刻WiFi信源发射的信号强度值x’m相关联,当误差项较小时,有xm=x’m,此时误差项干扰不明显。然而在实际情况中,由于式3中的误差项无法及时得到抑制或消除,导致误差不断积累,并对当前时刻接收的信号强度值xm产生的影响逐步增加。当误差积累进行到一定程度时,误差项Δ(xm)及Δ(xm-1)对当前时刻接收的信号强度值xm的影响程度达到最大,使得各个时刻都有xm≠x’m且xm≠xm+k,削弱了各时刻的信号强度值xm的相关性。同时由式2可知,自相关系数βk正比于乘积项(xm-μ)×(xm+k-μ),当信号集中各信号强度值xm相关性较强时,意味着该信号集中任意时刻的xm数值大小接近,即xm≈xm+k。此时有(xm-μ)×(xm+k-μ)≈(xm-μ)2,故这种情况下任意时刻的自相关系数βk值相近,并且由于xm和xm+k的数值差异不大,因此在自相关系数衰减过程中,其曲线表现为下降缓慢且平稳,如图4(a)、图4(d)所示。而当误差项Δ(xm)及Δ(xm-1)产生的误差积累较大时,会使得xm>>x’m或xm<
3 WiFi信号滤波算法的构建及分析
通过前文的分析可知,在WiFi信号传播的实际环境中,会出现两种不可预测的误差,分别是信号传播完成后遗留的残差与下次信号相叠加而产生的粗大误差以及信号传播环境中某些因素突然变化而出现的随机误差。然而在WiFi 信号实际传播过程中,还存在因实验设备自身的问题所引起的系统误差[6,7,10]。但是,这类误差由设备某种确定性原因所致,具有一定的问题指向性,可通过更换或调整实验设备解决。故系统误差不在这里的研究范围内,不考虑其对WiFi信号强度值的影响。
为确保采集得到的WiFi信号强度值的稳定性和准确性,结合前文的分析可知,信号传播过程中的误差并非为单一误差,故而在进行WiFi信号强度值处理时不能釆取单一的滤波算法,而需采用一套高效易行且复杂度较低的算法。结合现有的数据处理算法,并综合考虑本次实验所采集得到的样本数据量,决定将适用于采样次数大于10次的拉依达检测法和能够快速消除随机误差的卡尔曼滤波算法相结合,提出拉依达-卡尔曼滤波算法用以对各方位角的WiFi信号强度值进行处理,并将处理后的WiFi信号强度值的均值作为每一个方位角的位置指纹。
(1)拉依达-卡尔曼滤波算法构建
拉依达-卡尔曼滤波算法结合了拉依达检测法剔除数据中粗大误差的快速性和卡尔曼滤波算法在处理随机误差的稳定性,具有高效易行且时间、空间复杂度较低的优点,其算法流程,如图5所示。

图5 拉依达-卡尔曼滤波算法Fig.5 Laida-Kalman Filter Algorithm
由上图可知,拉依达-卡尔曼滤波算法分为如下两步:首先算法将计算各方位角WiFi信号集的均值μ与标准差σ,而后遍历当前WiFi信号集Xθi的各个元素并将其与均值μ求差,若差值小于标准差的3倍,则认为粗大误差对该信号强度值影响不大,将其保留并放入新的WiFi信号集X’θi,否则直接舍弃不用。而后依次设定卡尔曼滤波算法的卡尔曼系数Kg、测量噪声的协方差R、系统的过程噪声协方差Q、系统系数矩A、B及观测矩阵H,并进行信号强度值优化计算,同时将计算得到的最优值作为滤波后的信号强度值加以储存形成最终的WiFi信号集,并更新卡尔曼系数Kg直至滤波过程结束,其数学表达,如式(4)所示。

式中:X(m)ϵXθi={t1,…,tn,x1,…xn},(i=1,2,3,4)。其中,X(m|m-1)—m-1状态下X(m)的估计值,X(m-1|m-1)—m-1状态下X(m-1)的最优值,X(m|m)—m状态下X(m)的最优值,Z(m)-m状态下X(m)的实际值;U(m)—m状态下卡尔曼模型的控制变量;P(m|m-1)—m-1 状态下X(m|m-1)的协方差,P(m|m)—m状态下X(m|m)的协方差;I—单位矩阵;H—观测矩阵;Kg—卡尔曼增益;R—测量中噪声协方差;Q—系统的过程噪声协方差。
根据上述数学表达式,在选定WiFi信号集的初始状态后,算法就能快速计算该信号集中任意状态m的最优值X(m|m)及与之对应的协方差P(m|m),并对卡尔曼增益Kg进行实时更新以修正下次计算结果,直至算法将整个WiFi信号集遍历完成。
(2)各方位角WiFi信号强度值滤波分析
将拉依达-卡尔曼滤波算法的初始值X(0|0)设定为各WiFi信号集的起始信号强度值,并设定其初始协方差P(0|0)=10。当移动终端接收端位置不变时,其理想情况下所有时刻的信号强度值都应完全相同,由此可知系数矩阵A=1。同时由于控制量在该定位系统并不存在,故其控制矩阵U(m)=0。另外根据已有的文献表明,在信号传播过程中,可将绝大部分粗大误差及随机误差归类为高斯白噪声,故可令系统的过程噪声协方差Q=1e-4,测量中噪声协方差R=4。而后利用搭建好的拉依达-卡尔曼滤波算法依次各方位角的WiFi信号集进行数据处理,其结果,如图6所示。图6描述了各方位角WiFi信号集在拉依达-卡尔曼滤波算法处理前后的信号强度值分布。通过对比滤波前后信号强度值分布曲线,发现各方位角获取的原始信号强度值分布极不均匀,且信号强度值的上下阈值较大。而经拉依达-卡尔曼滤波算法处理后的信号强度值上下阈值较小,相邻采样次数下的信号强度值分布紧密,且其信号强度值分布曲线表现平稳,并能直观的找到滤波后信号集的分布规律。其原因为在拉依达-卡尔曼滤波算法中,其最优值X(m|m)由卡尔曼增益Kg控制,而其大小则受每次计算产生的估计值X(m|m-1)与信号集中实际值Z(m)的差值约束。当估计值X(m|m-1)与实际值Z(m)的差值较大时,此时的卡尔曼增益Kg增加,反之则降低。这就意味着,卡尔曼增益Kg的大小正比于每次计算的估计值与信号集中实际值的差值,使得由式(4)计算得到的每个相邻最优值X(m|m)的数值差异较小,最终表现为经滤波算法处理后的信号强度值分布较为集中,且分布曲线表现平稳。另外,从图6中还发现,经滤波后的信号强度值分布曲线,在起始位置出现了大幅上升或下降的趋势且其大小与原始数据极为接近。进一步对式(4)深入剖析,发现在滤波算法开始时,其初始值为信号集中的第一个数据,且经计算可知此时的卡尔曼增益Kg变化极小,使其估计值X(m|m-1)接近原始数据,导致计算得到的最优值X(m|m)与原始数据相差不大。而后随着算法的进行,当算法处理了一定数量的数据后,其卡尔曼增益Kg因前期计算产生的数值积累而出现显著变化,从而让最优值X(m|m)与原始数据出现差异,并促使相邻两次计算得到的最优值呈现一定规律性,最终表现为后续计算结果的分布曲线逐步到达平稳状态。

图6 各方位角WiFi信号集滤波后信号强度值分布Fig.6 Distribution of Signal Intensity after WiFi Signal Set Filtering
4 结论
(1)通过对不同方位角同距离处WiFi信号强度值的分布规律进行分析,发现信号在传播过程中因存在着相互干扰、衍射、反射等因素而产生粗大误差、残差和随机误差,无法使得信号在空间中以理想的状态进行传递,且其信号强度值分布不平稳且上下阈值差距较大。进一步对各方位角处WiFi信号强度值概率分布开展研究,发现不同方位角同距离处WiFi信号强度值均出现左侧数据拖尾现象,且由于各自方位角不同,使得各自均值μ和概率分布曲线的陡峭程度也不同。进而可知当前采集到的WiFi信号强度值概率分布不符合高斯分布,故而在其数据处理工作上,以高斯分布为基础的常见滤波算法难以胜任。
(2)这里对不同方位角同距离处WiFi信号强度值分布的统计特性进行分析,发现在信号传播过程中,前次信号传播后遗留的残差Δ(xm-1)和本次信号传播时产生的随机误差Δ(xm),也是影响信号强度值自相关性的重要因素。根据其统计特性分析结果,构建了能同时抑制粗大误差、残差Δ(xm-1)和随机误差Δ(xm)的拉依达-卡尔曼滤波算法。算法测试结果表明,经算法处理后的数据分布相较于原始数据分布,具有更高的线性平稳性且其数值分布更加均匀。表明了拉依达-卡尔曼滤波算法在WiFi信号强度值预处理上具有良好的性能,同时处理后的数据也为后续位置指纹库搭建工作提供了可靠的数据来源。
