时间尺度上变质量非完整系统的Lie对称性与守恒量

阙朝月，朱建青

(苏州科技大学数理学院，江苏 苏州 215009)

约束力学系统的对称性与守恒量具有重要的研究意义，在现代数学、力学、物理学中有着重要的地位，是分析力学的一个近代发展方向[1].时间尺度是一个较为新颖的课题，它统一和拓展了连续和离散系统.在时间尺度上建立的动力学方程将连续系统的微分方程与离散系统的差分方程融为一体，使得动力学方程具有了更为一般的性质.结合时间尺度与动力学系统，近年来有关学者陆续给出了时间尺度上的一些理论[2-7].

随着空间技术及其它工业的发展，变质量系统应用得越发广泛.19世纪中叶，人们提出了变质量问题.1897年，俄国学者Мещерский建立了变质量质点的动力学基本方程.1929年，苏联力学家Циолковский提出用多级火箭实现宇宙飞行，对变质量力学作出了重要贡献.对于变质量系统的对称性与守恒量，人们已经给出了变质量系统的Noether理论、Lie对称性理论、Mei对称性理论等[8-15]，而时间尺度上的变质量非完整系统的Lie对称性理论还未有涉及.本文讨论了时间尺度上变质量非完整系统的Lie对称性与守恒量，利用时间尺度上微分方程在无限小变换下的不变性给出了时间尺度上变质量非完整系统的Lie对称性确定方程，当存在规范函数满足结构方程时，可解得相应守恒量.最后给出算例进行说明．

1 时间尺度上变质量系统的D’Alembert-Lagrange原理与Routh方程

1)时间尺度上变质量系统的D’Alembert-Lagrange原理

在时间尺度T上，设变质量力学系统由N个质点所构成.在时刻t，变质量系统的质量可表示为

(1)

注：本文所涉时间尺度上符号可参考文献[16]．

在t+Δt，由质点分离(或并入)的微粒质量为Δmi，则时间尺度上第i个质点的Мещерский方程[17]可表示为

(2)

(3)

其中ui表示质点分离(或并入)的微粒对应于质点本身的相对速度．

将式(2)两端点乘虚位移δri，并将方程对i进行求和，则得到

(4)

理想约束条件为

(5)

将式(5)代入式(4)则可得如下方程

(6)

设时间尺度上变质量系统的位形由n个广义坐标qs(s=1，…，n)来确定，则矢径

ri=ri(t，qs) (i=1，2，…，N;s=1，2，…，n).

(7)

虚位移条件为

(8)

将式(8)代入式(6)得

(9)

在时间尺度上，系统的动能可表示为

(10)

又由文献[16]求导法则得

(11)

从而可知

(12)

(13)

(14)

将式(12)与(14)代入式(9)，则可得到时间尺度上变质量完整系统的D’Alembert-Lagrange原理的Lagrange形式

(15)

对于完整约束系统，式(15)中的δqs是相互独立的，从而变质量完整系统在时间尺度上的运动微分方程可表示为

(16)

其中

(17)

(18)

(19)

将Qs分为有势的Q′s和非有势的Q″s，有

Qs=Q′s+Q″s，

(20)

设L=T-V，并将式(20)代入式(16)，从而有

(21)

2)时间尺度上变质量系统的Routh方程

假设变质量系统的运动受到g个理想非完整约束

fβ(t，q，qΔ)=0(β=1，…，g)，

(22)

约束(22)施加于虚位移δqs上的限制条件可表示为

(23)

利用式(21)，由文献[18]不定乘子法可得时间尺度上变质量系统的Routh方程

(24)

由式(22)和(24)可求得λβ为t、q、qΔ的函数，将λβ代入(24)则可得到

(s=1，…，n).

(25)

称方程(25)为时间尺度上变质量非完整系统(22)(24)相应于完整系统的运动方程．

假设此时间尺度上变质量非完整系统非奇异，即

(26)

展开式(25)，则可求得所有的广义加速度，记作

(27)

2 时间尺度上变质量非完整系统的Lie对称性与守恒量

在时间尺度上，引入无限小变换

t*=t+εξ0(t，qs)，

(28)

引入时间尺度上生成元向量[19]

(29)

它的一次扩展式为

(30)

二次扩展式为

(31)

于是方程(27)在变换(28)下的不变性可概述为

(32)

从而有确定方程

(33)

定义1若生成元ξ0、ξs使确定方程(33)成立，则称变换(28)为与时间尺度上变质量非完整系统相应的完整系统的Lie对称变换，相应的对称性称为Lie对称性．

考虑到非完整约束，式(22)在无限小变换(28)下的不变性可概述为限制方程

X(1)(fβ(t，q，qΔ))=0.

(34)

约束(22)施加于虚位移δqs上的限制(23)对生成元存在如下附加限制方程

(35)

定义2若生成元ξ0、ξs使确定方程(33)和限制方程(34)成立，则相应的对称性称为时间尺度上变质量非完整系统的弱Lie对称性．

定义3若生成元ξ0、ξs同时使确定方程(33)、限制方程(34)和附加限制方程(35)成立，则称相应的对称性为时间尺度上变质量非完整系统的强Lie对称性．

定理1对于使确定方程(33)成立的生成元ξ0、ξs，当满足结构方程

(36)

的规范函数G=G(t，q，qΔ)存在时，时间尺度上变质量非完整系统有如下形式的守恒量

(37)

证明由文献[20]在时间尺度上有

于是

证毕．

定理2如果生成元ξ0、ξs使确定方程(33)和限制方程(34)成立，当满足结构方程(36)的规范函数G=G(t，q，qΔ)存在时，时间尺度上变质量非完整系统有形如式(37)的弱Lie对称性守恒量．

定理3如果生成元ξ0、ξs同时使确定方程(33)、限制方程(34)和附加限制方程(35)成立，当满足结构方程(36)的规范函数G=G(t，q，qΔ)存在时，时间尺度上变质量非完整系统有形如式(37)的强Lie对称性守恒量．

若T=R，有σ(t)=0，μ(t)=0，式(33)则成为经典变质量非完整系统的Lie对称性确定方程[21]

(38)

式(36)则成为经典变质量非完整系统的Lie对称性结构方程[21]

(39)

式(37)成为经典变质量非完整系统的Lie对称性守恒量形式[21]

(40)

3 算例

在时间尺度T={t:t∈N∪{0}}上研究一个变质量质点，其质量为

m=m0e-t(m0=const),

(41)

Lagrange函数为

(42)

受到非完整约束

(43)

非势广义力为

(44)

假设微粒分离的绝对速度为零，即

u=-rΔ=0,

(45)

试讨论该变质量非完整系统在时间尺度上的Lie对称性．

第一步，求λ并解出广义加速度.由式(17)，(19)和(44)可得

P1=P2=0，Φ1=Φ2=0,

(46)

方程(24)，(42)和(44)给出

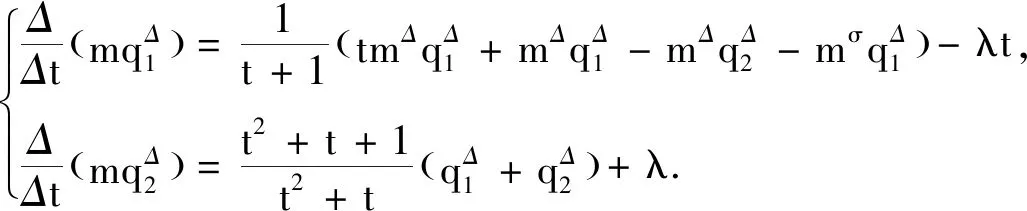
(47)

由式(43)(47)解得

(48)

从而有

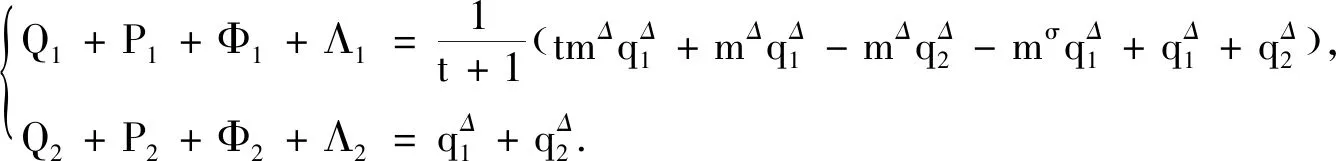
(49)

将式(49)代入式(47)解得广义加速度

(50)

第二步，求生成元.将式(50)代入确定方程(33)得到

(51)

方程(51)有如下解

ξ0=0，ξ1=0，ξ2=1.

(52)

第三步，检验生成元是否满足限制方程与附加限制方程.由式(34)(35)(43)可得限制方程与附加限制方程分别为

(53)

(54)

可知生成元(52)能够使限制方程式(53)成立，但不满足附加限制方程(54)，从而相应的对称性为时间尺度上变质量非完整系统的弱Lie对称性，对应的守恒量为弱Lie对称性守恒量．

最后，求得规范函数并计算守恒量.将式(52)代入结构方程(36)可得

(55)

由此求得规范函数

G=-q1-q2,

(56)

守恒量(37)成为

(57)

4 结束语

本文讨论了时间尺度上变质量非完整系统的Lie对称性与守恒量.基于时间尺度上变质量系统的D’Alembert-Lagrange原理，建立了时间尺度上变质量系统的Lagrange方程，进一步给出了系统的Routh方程与Lie对称性的定义和定理，根据Lie对称性，利用规范函数求出相应的Lie守恒量.本文提供了一种研究时间尺度上变质量系统对称性的新方法，其思想方法还可推广到时间尺度上其它力学系统的对称性研究中．