基于博弈论的认知无线网络中一种功率控制算法

刘觉夫，王建夏，陈 娇

(华东交通大学信息工程学院，南昌 330013)

随着现有和新的通信业务的发展，固有的频谱分配方式已经不能够满足这些业务的需求，认知无线电的提出在一定程度上缓解了这种频谱资源紧缺的局面.认知无线电能够与周围环境进行交互，可以动态的感知频谱空穴，从而使次用户(Secondary User，SU)在不对主用户(Primary User，PU)造成严重干扰的情况下采用机会接入的方式使用授权用户的授权频段[1-4].在underlay模式中，次用户使用主用户的授权频段时必定会对主用户和其它次用户产生干扰，功率控制是解决干扰问题的关键.多个次用户在使用主用户授权频段时会产生竞争，博弈论的引入可以很好的解决竞争问题.

文献[5]提出了K-G(Koskie-Gajic)算法，该算法降低了用户的发射功率，但是并不能满足所有用户的信干噪比(Signal-to-Interference-Noise Ratio，SINR)阈值，且未充分的考虑到次用户的公平性.文献[6]对NGP-MSFLA算法进行了改进，改进后得算法综合考虑了信干燥比和干扰门限，设计了一种非线性的公平性功率控制算法.文献[7]采用干扰消除技术减少认知网络的中断概率，但该算法设计模型中只允许存在一个次用户，这与多数实际情况不符.上述研究虽然改进了非合作功率控制算法，但认知系统的整体性能仍然有待提高.

针对上述问题，本文受文献[8]的启发将信道状态引入到代价函数中，且综合考虑发射功率、信干燥比、干扰门限和系统公平性，提出了一种改进的功率控制算法，该算法可快速收敛，具有抗背景噪声能力，且提高了系统的吞吐量.

1 频谱共享模型

如图1所示，本文采用underlay模式，次用户和主用户可以同时使用主用户的授权频谱资源.本文假设在认知系统中采用CDMA的通信方式，且只研究上行链路.该模型中有一个主用户，主用户与主基站相互通信，有一个次用户，次用户与次基站相互通信.次用户通信时会对其它用户造成干扰，为保证主用户的正常通信，主用户把次用户当成噪声处理，次用户对主用户造成的干扰综合要小于干扰门限.因此，通过功率控制技术，既要保证次用户的正常通信，又不能对主用户造成严重干扰.

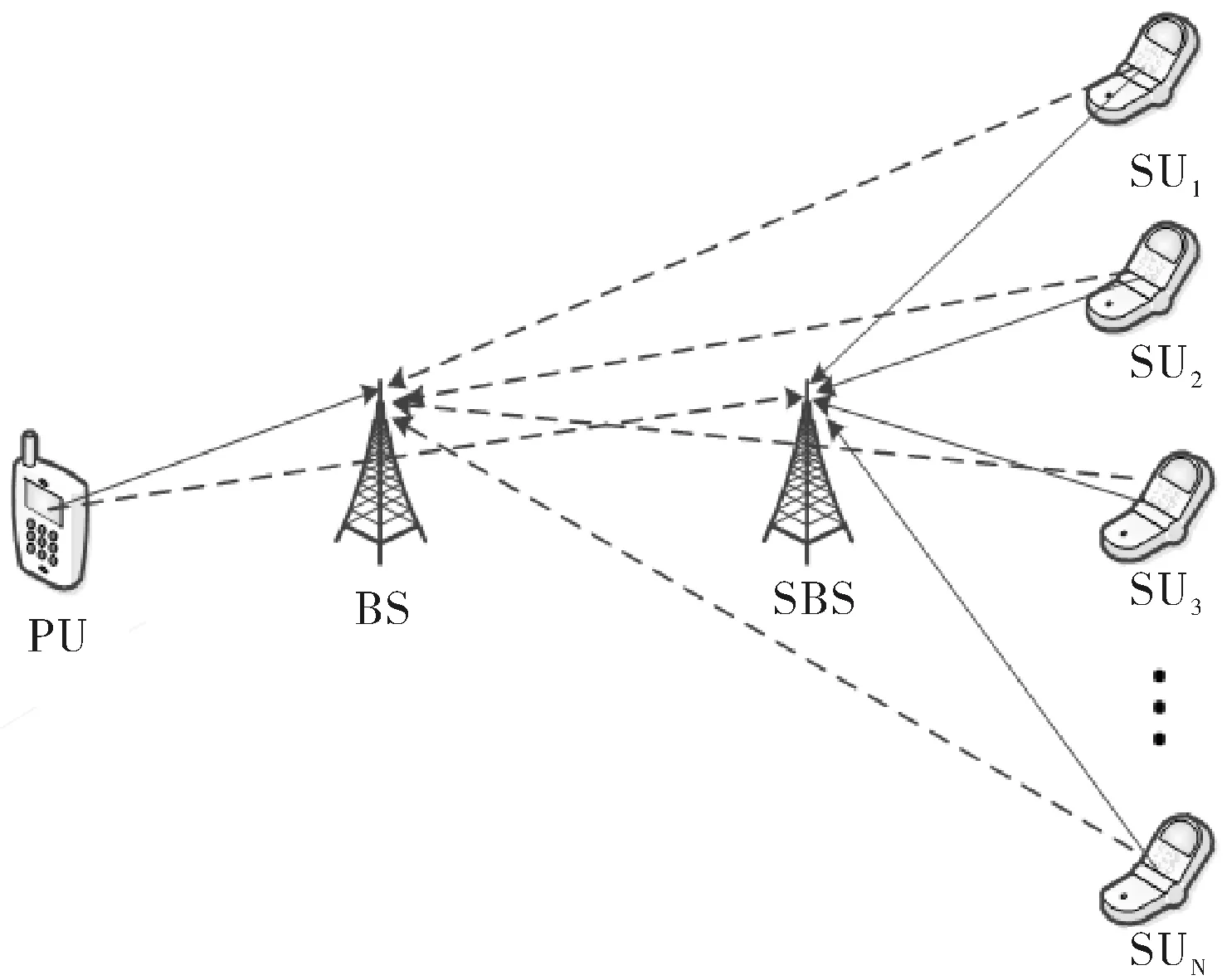
图1 认知网络频谱共享模型Fig.1 Spectrum sharing model of cognitive network

假设主用户i到主基站的链路增益为hi，次用户j到次基站的链路增益为hj，则次用户i的信干燥比(Signalto Interference Plus Noise Ratio，SINR)可以表示为：

(1)

其中，cij为各用户扩频码之间的相关系数，δ2为高斯白噪声.

定义

(2)

由式(1)和式(2)得：

(3)

在认知无线网络中，为保证主用户、次用户的QoS和正常通信需要满足下列两个条件：

2 非合作博弈功率控制算法

2.1 传统的功率控制算法

在认知无线网络(Cognitive Radio Network，CRN)系统中，次用户往往是理性的，即次用户为了增大自身收益会私自提高发射功率，而不管对其它用户的影响.次用户的自私性使得次用户是非合作的，这种非合作的博弈可以用非合作博弈知识进行建模.令G={N，{pi}，{Ui(p)}}，其中，N为用户个数，pi为用户发射功率集合，Ui(p)为用户的收益函数[9-11].

文献[5]提出的K-G算法是在SINR平衡算法的基础上，把发射功率作为效用函数的一个参考项，对私自提高发射功率的用户加大惩罚，K-G算法的效用函数为：

(4)

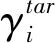
文献[12]在K-G算法的基础上作出了改进，提出了一种基于SINR和发射功率的功率控制算法，其效用函数为：

(5)

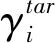
2.2 本文算法

本文在传统的功率控制算法的基础上，将信道状态引入到效用函数中.信道状态是指用户受到的干扰与链路增益的比值，表示为：

(6)

由式(6)可知，在链路增益不变的情况下，用户受到的干扰越大，信道状态值越大.所以对实际情况而言，在其它因素不变的情况下，信道状态值越小越好.本文借鉴K-G算法、文献[12]算法和信道状态的概念，设计出新的效用函数K-G-New，表示为：

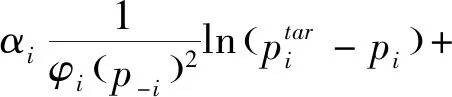
(7)

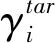
3 纳什均衡的存在性和唯一性证明

由博弈论中纳什均衡的定义[13-15]可知，当次用户的博弈达到纳什均衡点时，整个CRN系统总体收益最大.在现实情况中，由于次用户往往是理性的，所以次用户在选择策略时会最小化自生代价，因此，次用户达到纳什均衡点必须满足：

(8)

式(8)中所求的满足条件的pi即为最佳策略.本文采用拉格朗日算法求纳什均衡解.对式(7)中pi求一阶偏导数得：

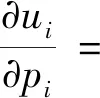
(9)

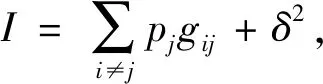
(10)

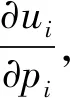
(11)

(12)

由式(11)和式(12)得：

(13)

唯一性证明令p=f(p)，当f(p)满足下列条件时收敛：

1)f(p)>0；

2)若p1>p2，则f(p1)>f(p2)；

3)若∀τ>1，则τf(p)>f(τp).

证明令

2)令p1>p2，则:

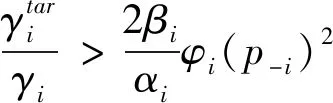
3)设存在τ，对任意的τ满足τ>1，则:

上式中所有参数均大于零，且τ>1，所以τf(p)>f(τp)成立.

综上所述，f(p)满足函数收敛的三个条件，所以该算法存在唯一性.

存在性证明由隐函数定理得：

F(pi，p-i，gii，gij，αi，βi，δ)=0=

则有：

(14)

4 一般迭代法求取纳什均衡解

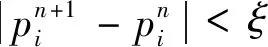
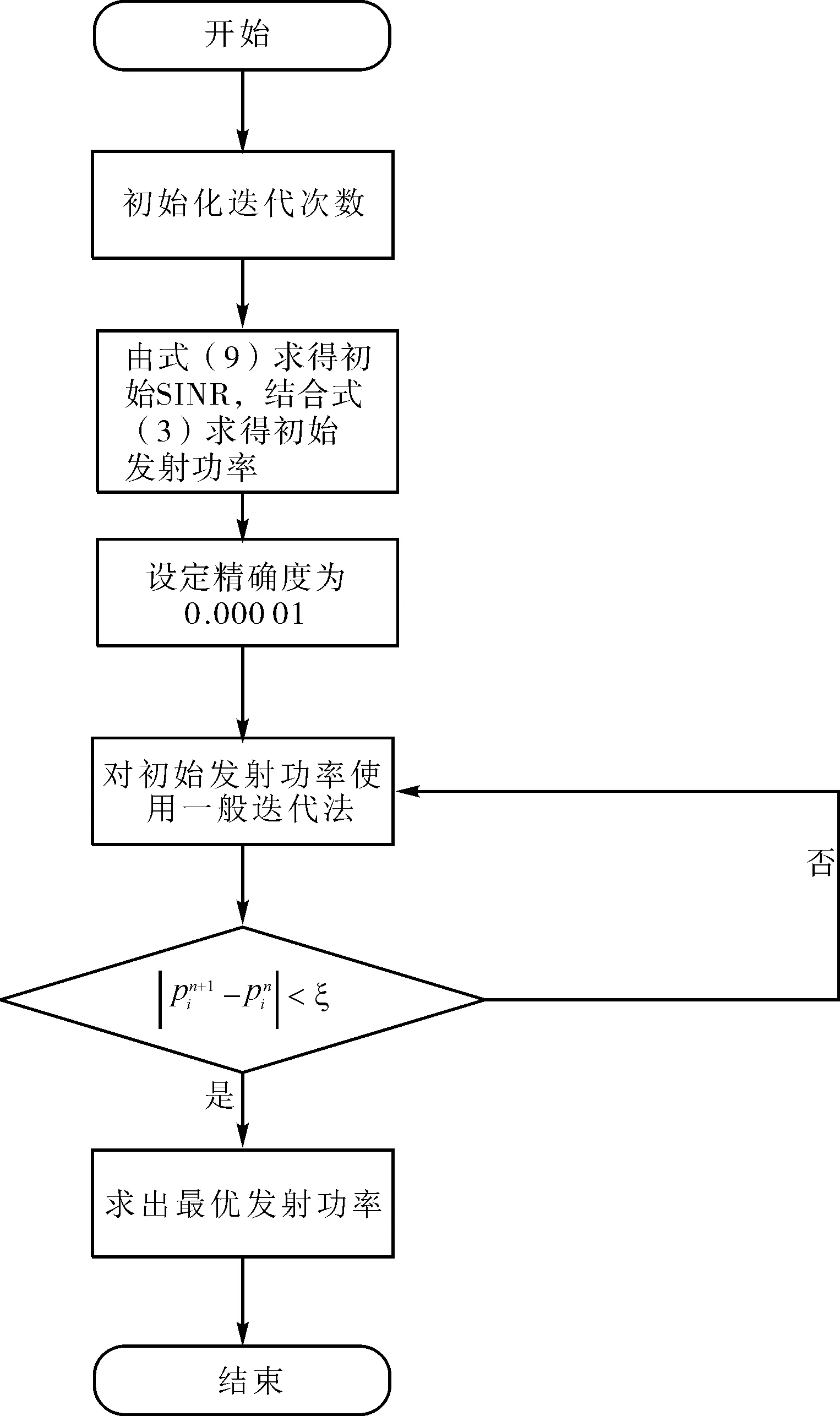
图2 算法流程图Fig.2 Algorithm flowchart

5 仿真实验结果与分析

本文采用Matlab进行仿真实验，实验中取两个参照对象，分别是K-G算法和文献[12]所提算法.假设次用户以次基站为中心随机的分布在半径为2 km的覆盖范围内，次用户数N=20.为使实验简单化，背景噪声固定为δ2=4×10-4，认知用户的初始发射功率p(0)=10-10W，迭代误差ξ=10-5.信道增益定义为：

(15)

式中，d为用户离基站的距离，A和m与信道的衰减有关，取m=3，A=5×10-4.单位带宽吞吐量公式定义为：

(16)

式中，T为单位带宽吞吐量，γi为次用户信干燥比，为便于计算，本文将带宽设定为1 kHz.

图3为三种算法收敛性的比较.如图所示，文献[12]中的算法大概在第八次迭代时收敛，K-G算法和本文算法大概在第七次收敛.三种算法在收敛性方面差异不是很大，都可以快速收敛.虽然在收敛性差不多的情况下，K-G算法的发射功率比文献[12]和本文算法低很多，但是K-G算法没有考虑到阈值问题，使得很多用户的发射功率太低，不能进行正常通信.本文所提K-G-New算法在保证用户正常通信的情况下，与文献[12]算法相比，在一定程度上降低了用户的发射功率.

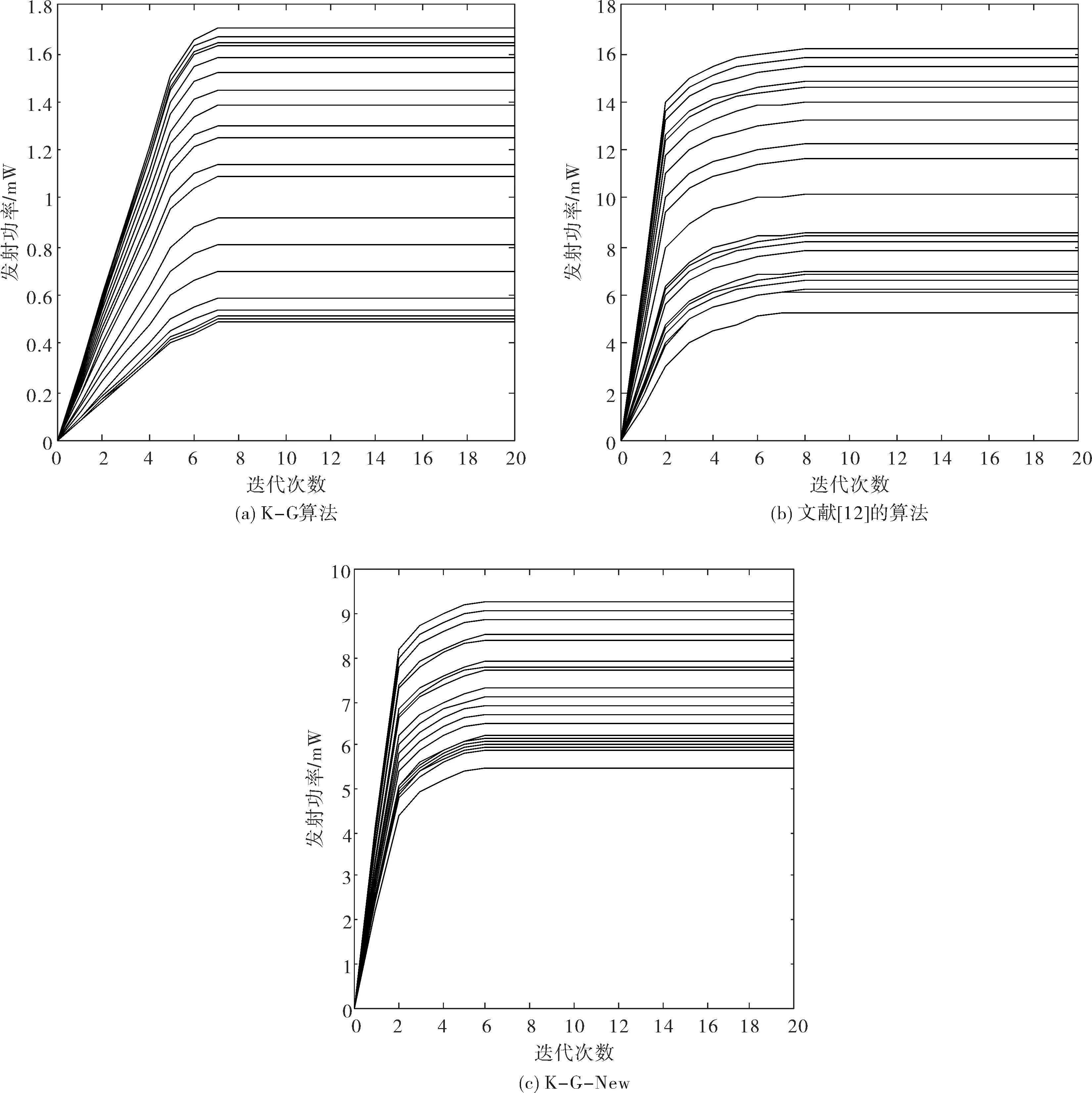
图3 三种算法收敛性Fig.3 Convergence of the three algorithms

图4为所提K-G-New算法、K-G算法和文献[12]算法随着迭代次数的增加次用户受到的总干扰的变化趋势.在迭代次数相同的情况下文献[12]算法中次用户受到的干扰最大，K-G算法受到的干扰最小，但K-G算法一味地降低发射功率，使得部分用户SINR低于阈值，不能满足正常通信.本文所提K-G-New算法在保证用户正常通信的情况下，引入信道状态的概念，使得次用户受到的干扰有所下降.

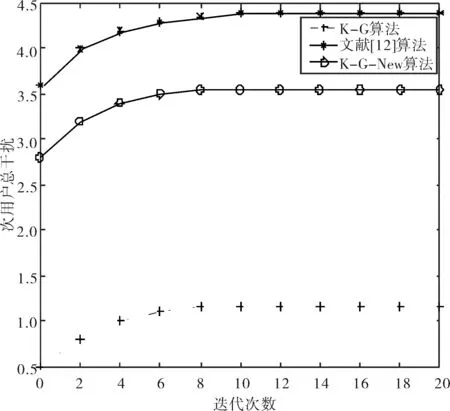
图4 迭代次数与次用户总干扰关系Fig.4 Relationship between the number of iterations and the total interference of secondary users

图5 为次用户平均发射功率随着噪声变化的趋势图.从图中可以看出随着噪声的增大，三种算法的平均发射功率都会增大，K-G算法的变化趋势最为缓慢，这是因为K-G算法没有考虑到信干燥比门限，而K-G-New算法和文献[12]中算法都能保证随噪声增大，用户的SINR大于最低SINR门限，但K-G-New算法发射功率比文献[12]略低.

图5 平均发射功率随噪声变化趋势Fig.5 The variation rend of average transmit power with noise

图6 为随着次用户数量的增加三种算法吞吐量的变化趋势图.由图可知，随着次用户数量的增加，三种算法的吞吐量会先急剧增加后缓慢增加，这是因为随着用户数量的增加，用户间的干扰也会增大.与K-G算法和文献[12]算法相比，K-G-New算法吞吐量最大.

图6 吞吐量比较Fig.6 Throughput comparison

3 结束语

本文在K-G算法和文献[12]所提算法的基础上结合信道状态的概念设计了一种新的功率控制算法.仿真实验结果表明，该算法收敛速度较快，在保证用户正常通信的前提条件下，进一步降低了用户的发射功率，且具有良好的抗干扰能力和较大的吞吐量.然而，本文只研究了一个主用户多个次用户下的功率控制，为了满足现实情况，下一步将考虑将单个主用户扩展到多个主用户的情况.