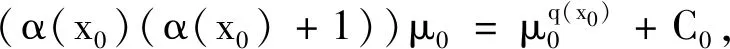带非齐次项和变指数椭圆方程边界爆破解问题

孔豪杰，沃维丰，马飞遥

(宁波大学数学与统计学院，浙江 宁波 315211)

椭圆边界爆破问题已经被大量国内外研究者研究[1-4]，其中含非齐次项的问题近年来受到较多关注[5-8].文献 [5]中Melin和Rossi研究了变指数的椭圆方程边界爆破问题

得到了该方程解的存在性，边界渐进行为和唯一性．

本文基于文献 [5]和文献 [6],研究了具有非齐次项的变指数的椭圆方程边界爆破解

(1)

其中,Ω是N中的光滑有界区域，以及h(x)∈C(Ω)且可能无界和异号．

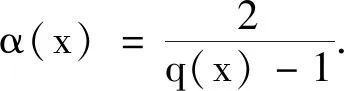
定理1假设q(x)>1，且h(x)满足

(2)

则问题(1)至少存在一个解u．

定理2假设q(x)>1，且存在常数C>0，使得h(x)满足

(3)

其中0<β<1，则问题(1)存在一个正解．

定理3假设q(x)>1，且h(x)满足

(4)

其中x0∈∂Ω，则问题(1)不存在正解.

1 定理的证明

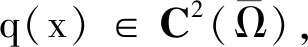
(5)

至少存在一个正解.

证明首先考虑边值问题

(6)

下面将证明{un}在区域Ω的紧子集里是有界的.

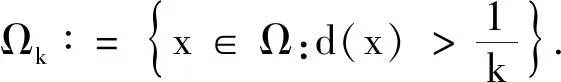
(7)

(8)

根据引理1，问题(8)存在一个解，记vk.那么vk很明显是问题(8)的一个上解．

接下来构造下解，利用条件(2)，取一个常数A，在区域U(∂Ω)内使得α(x)(α(x)+1)A>Aq(x)+L.选取ε充分小，在区域U(∂Ω)内使得

α(x)(α(x)+1)A>Aq(x)+L+ε.

(9)

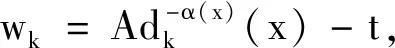
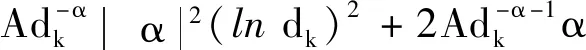
为了证明wk是一个下解，只需要在区域Ωk内检验下面不等式成立：

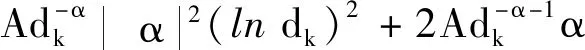
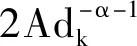
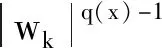
(10)

由条件(2)在区域Ωδ0={x∈Ω|d(x)<δ0}内，取足够小的δ0使得

因为d在区域Ωδ0内是C2函数和|d|=1.令δ∈(0，δ0).在区域Ωδ={x∈Ωk|d(x)<δ}∩U(∂Ω)内由条件(9)有

2Adkααlndkd-

2Adkα

Aq(x)+L+ε.

在区域Ωδ内，当dk足够小时，有

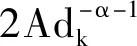
(11)

另一方面，在区域Ωδ=ΩΩδ内，存在一个正常数C，使得

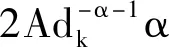
(12)

在区域Ωδ内，当t≥t0且t0足够大时，有

(13)

通过(11)，(12)和(13)式显然不等式(10)成立.因此，wk是问题(7)的一个下解．

在区域Ωk内，由比较原理得wk≤vk.因此，应用上下解方法可得问题(7)存在解uk，且区域Ωk内满足:wk≤uk≤vk.

定理2的证明首先考虑问题

(14)

根据文献[5]的定理3，问题(14)存在唯一正解V.令w是问题

的解，其中h+(x)=max{h，0}.由于在区域Ω内w<0，通过条件(3)，取C充分小，使得|w|<η，其中η为问题(14)解的最小下界，有V+w>0.则

Δ(V+w)=Vq(x)+h+(x)≥(V+w)q(x)+h(x),

所以V+w是问题(1)的下解.由定理1可知问题(1)存在一个解u，通过比较原理可得在区域Ω内u>V>0，因此问题(1)存在一个正解．

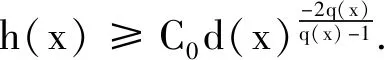
(15)

的一个下解.V表示问题(14)的唯一正解，所以V是问题(15)的一个上解，通过比较原则，在区域Ω0内u≤V.因此利用上下解的方法可得问题(15)存在一个正解，记v.在区域Ω0内且满足

v(x)≤Cd0(x)-α(x)，

(16)

其中d0(x)=dist(x，∂Ω0).

接下来将证明问题(15)满足(16)的条件下不存在任意非负解.不失一般性，假设x0=0，且在x0点从内部指向边界∂Ω的单位法向量υ=e1(其中e1表示正则基中第一个向量).设{cn}是任意一个收敛到零的正序列.令xn=cne1，并引入函数

其中Dn={y∈N|cny∈Ω0}.当n足够大时xn∈Dn，d(xn)=cn和当n→∞时，N|y1>0}.很明显，函数vn(y)满足:

(17)

和

(18)

(19)

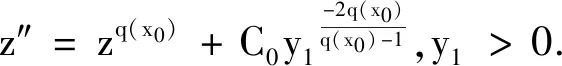
(α(x0)(α(x0)+1))μ-(2α(x0)+1)μ′+μ″=

μq(x0)+C0.

(20)