不确定性下基于多工况优化的可控性换热器网络综合

2020-05-15李晨莹刘琳琳张磊顾偲雯都健

化工学报 2020年3期

李晨莹，刘琳琳，张磊，顾偲雯，都健

（大连理工大学化工学院化工系统工程研究所，辽宁大连116024）

引言

常规换热器网络综合以经济性为目标进行参数和结构优化[1-3]，这会导致各换热设备之间存在强烈耦合关系，进而造成潜在的控制困难，使得可控性研究失去了原本的意义[4]。此外，常规换热器网络综合是在固定操作条件下进行的[5]。然而在实际工业环境中，来自上游过程流股以及环境本身所带来的不确定性因素是不可避免的。这些扰动会使得换热器网络的实际优化性能产生偏差甚至操作不可行[6]。因此，研究能够抵御扰动的可控性换热器网络综合问题是十分重要的。

一个被控变量与一个操纵变量的配对构成控制回路，一系列控制回路构成了控制结构[7]。由于换热器网络的多变量特性，控制回路之间的相互作用会对换热器网络可控性产生严重的负面影响。Escobar 等[8]认为可控性是换热器网络的一种能力，高度可控的换热器网络能够减少其潜在的控制困难，例如时延和相互作用。在此背景下，研究者们致力于设计控制回路间相互作用最小的控制结构，以此来提高换热器网络的可控性[9]。2011 年，罗雄麟等[10]通过依次求解非方相对增益矩阵(relative gain array, RGA)，提出了换热器网络旁路位置优化方法。其中给出了用以选择旁路的启发式规则，有效地简化了求解运算过程。2016 年，在图论的研究背景下，Kang 等[11]基于相对阶提出了一种凝聚层次聚类方法以设计控制结构。此外，还引入模块化的概念来评估结果的紧凑性和分离性，从而识别最优的控制结构。2017 年，Braccia 等[12]通过平方偏差和以及净负荷评估，提出了多变量控制结构设计方法。

然而，换热器网络的可控性不仅与控制结构相关，还严重依赖于网络结构[8]。近年来，研究者们发现了换热器网络结构对可控性的重要性并对其影响进行探究。2016 年，Masoud 等[13]提出了一种分步策略，用于设计具有最小年度总费用(total annual cost, TAC)和最佳可控性的换热器网络。同年，Bakar 等[14]通过优化最小传热温差来同时考虑换热器网络的经济性和可控性。然而，之前的研究只针对换热器网络结构对其可控性的影响，忽略了两者间相互作用，导致在综合阶段仅得到具备优越经济性能的换热器网络，而无法搜索可控性换热器网络综合问题的最优解。更重要的是，在不确定性因素的干扰下，无法保证其所得结果的操作可行性[15]。

换热器网络的不确定性因素主要包括流股入口温度和热容流率等[16]。对换热器网络进行柔性分析和改造是使其能够抵御不确定性因素的有效方法[17]。2013 年，Escobar 等[8]定义了有效柔性指数，用于衡量包含控制结构的换热器网络的柔性程度。如不满足柔性需求，则进行网络结构和控制结构的改造。2019 年，Gu 等[18]通过考虑流股出口温度的变化范围，设计能够抵御多扰动的换热器网络。

本文考虑换热器网络结构与可控性之间的相互作用，基于多工况优化，深入探究不同决策变量对换热器网络经济性和可控性的影响，并以柔性指数衡量换热网络的操作可行性，提出抵御不确定性因素扰动的可控性换热器网络综合方法。该方法旨在探索换热器网络经济性和可控性之间的权衡，并得到抵御不确定性因素扰动的可控性换热器网络。

1 问题描述

不确定性下基于多工况优化的可控性换热器网络综合问题描述为：已知一系列冷热流股，其中各流股的进出口温度、热容流率、传热膜系数给定。已知不确定性因素及其波动范围，已知最小传热温差。该问题依据多工况优化，致力于得到具有最小年度总费用的可控性换热器网络，并且该网络能够在指定的不确定性因素波动下保证其操作可行性。

本文工作基于以下假设：(1)忽略流股的压力降和其他的流体动力学因素[19]；(2)旁路开度为操纵变量，流股出口温度为被控变量；(3)考虑不确定性参数波动[20]。

2 不确定性下基于多工况优化的可控性换热器网络综合方法

首先，给出两条启发式规则来充分考虑换热器网络结构与可控性之间的相互影响，进行可控性换热器网络综合得到初始换热器网络，标记为HEN1。其次，基于不同工况调控，优化决策变量以权衡换热器网络的经济性和可控性，得到标记为HEN2 的换热器网络。最后，通过柔性指数判断HEN2 在不确定因素扰动下的操作可行性，若不可行，则辨识HEN2 的临界操作点并在其上进行网络结构和控制结构的改造，得到最终换热器网络，标记为HEN3。

3 数学模型

3.1 可控性换热器网络综合模型

本文基于Yee 等[21]提出的无分流分级超结构开展换热器网络综合研究。不同之处在于，本文采用的超结构中，各换热器冷热流股两侧均可放置旁路，且考虑非等温混合，超结构如图1所示。

3.1.1 目标函数以换热器网络年度总费用最小为目标函数进行可控性换热器网络综合。年度总费用包括投资费用和操作费用，投资费用分为换热设备的固定安装费用和面积费用，如式(1)所示。

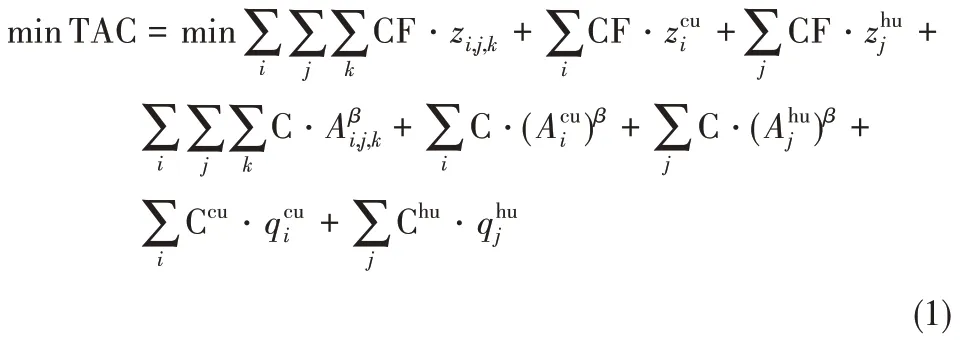
其中，二元变量zi,j.k、zcui、zhuj分别表示换热器、冷却器、加热器的存在性。当匹配存在时，二元变量取值为1，否则取值为0。CF 为换热器的固定安装费用；C 为换热器的面积费用系数；Ccu、Chu分别为单位冷热公用工程费用[22]。

3.1.2 约束条件过程模型是综合模型中不可或缺的约束条件，其用于描述换热器网络。过程模型包括一系列等式和不等式约束，例如热平衡方程、质量平衡方程、温度可行性约束等，完整的约束条件详见Grossmann 教授课题组的研究工作[8]。此外，本文提出用于提高换热器网络可控性的启发式规则，如下所示。

(1)避免同一换热器冷热两侧流股出口温度同时成为被控变量

显然，这种情况将增加相应控制回路间相互作用，导致换热器的出口温度变化极为复杂，从而降低换热器网络的可控性。该规则可描述为式(2)～式(5)

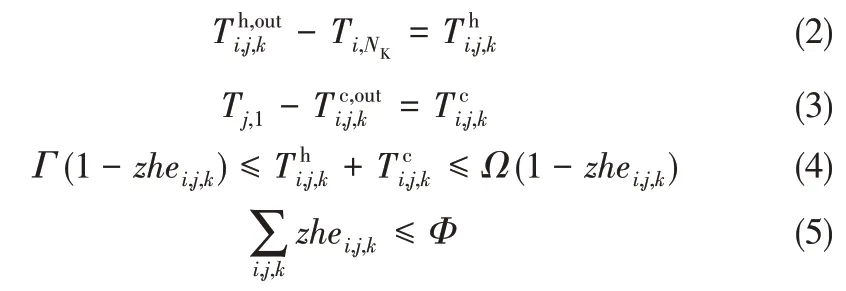
其中，Tc,outi,j,k和Th,outi,j,k分别是换热器冷热流股侧的出口温度；Ti,NK和Tj,1分别是第i 条热流股和第j 条冷流股的出口温度;Thi,j,k是换热器热端出口温度与第i条热流股出口温度的差值;Tci,j,k是第j 条冷流股出口温度与换热器冷端出口温度的差值。当Tc,outi,j,k和Th,outi,j,k同时成为被控变量时，二元变量zhei,j.k取值为1。参数Γ和Ω是惩罚因子，参数Φ由网络规模确定。

(2)优先选择对被控变量有直接影响的旁路开度作为操纵变量

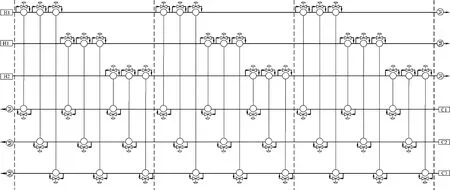
图1 考虑所有潜在旁路的无分流分级超结构Fig.1 Nonsplit three-stage superstructure involving all possible bypasses

Masoud 等[13]指出放置在流股末端换热器上的旁路对该出口温度有直接影响。因此，当选择这些旁路的开度作为操纵变量时，相应的控制回路可对换热器网络的温度调节提供快速的响应，减少了潜在的控制困难，从而改善了换热器网络的可控性。而且这种旁路能够有效地缓解控制回路间相互作用。否则，当旁路放置在远离流股末端的换热器上时，所产生的控制回路将受到下游其他控制回路的负面影响，其本身的温度变化也将顺序传递至下游换热器。该规则可描述为式(6)、式(7)。

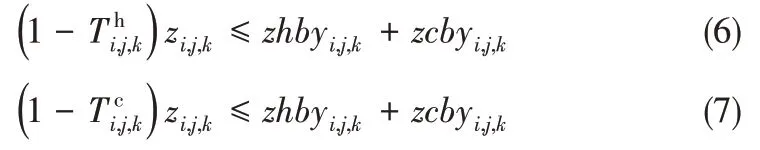
二元变量zhbyi,j,k和zcbyi,j,k表示换热器上冷热流股两侧旁路的存在性。当热端流股上存在旁路时，zhbyi,j,k取值为1。当冷端流股上存在旁路时，zcbyi,j,k取值为1。

3.2 控制结构设计

相对增益是用来衡量操纵变量与被控变量之间相互作用的尺度[23-24]。因此，通过计算相对增益矩阵可用于配对操纵变量与被控变量，以便获得具有最小控制回路间相互作用的控制结构[25]。相对增益矩阵通过增益矩阵G 获得，如式(8)所示[26]。矩阵G 的行表示换热器网络的被控变量，列是操纵变量。矩阵G 的元素gp,q描述第p 个被控变量与第q个操纵变量的关系[27]。

选择相对增益矩阵的元素值等于1或者接近于1 来构成的控制结构具有最小的控制回路间相互作用。故通过两者间差值构建新的可控性指标来实现控制结构的优化设计，即相对增益矩阵数(relative gain array number,RGAN)，其计算公式如式(9)所示[28]

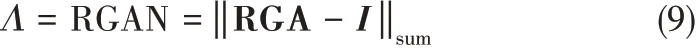
3.3 换热器网络可行性分析

常规换热器网络综合是基于固定操作条件开展的。然而，换热器网络在实际工业环境中会不可避免地受到不确定性因素的干扰，导致其实际优化性能产生偏差，甚至操作不可行[29-30]。因此，在不确定性因素的干扰下，保证可控性换热器网络的操作可行性是至关重要的。

柔性指数可以定量地描述过程系统所能承受扰动的最大偏差，指最大偏差与其特定变化范围的比值，其普适性强，是不确定性领域中里程碑式的成果。当柔性指数大于等于1，表示不确定性因素在一定范围内波动时系统仍能维持运行。描述柔性指数的模型如式(10)～式(13)所示[31]

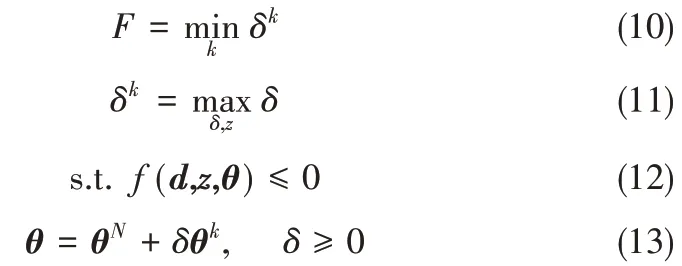
式中，δk为最大允许偏差；f 表示与设计变量d、控制变量z、不确定性参数θ相关的不等式约束。

4 算例分析

算例数据来自Li 等[32]，包括冷热流股各3 条，冷热公用工程各1 条，过程流股数据如表1 所示。最小传热温差为10 K，换热设备投资费用的计算式为COST=8000+800A0.8USD，冷热公用工程的费用分别为10 USD·kW-1·a-1和70 USD·kW-1·a-1。不确定性参数为流股H1,H3,C1 和C2 的入口温度，其波动范围为±10 K。

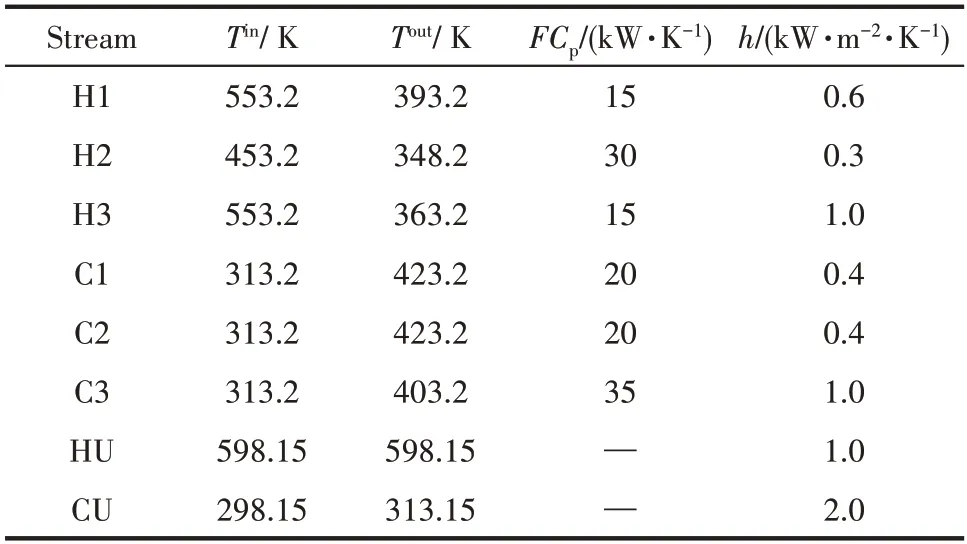
表1 过程流股数据Table 1 Parameters of process streams

4.1 可控性换热器网络综合

首先，在标准操作条件下进行可控性换热器网络综合，旁路开度下限设置为0.1[13]，综合得到的换热器网络标记为HEN1，如图2 所示，其相关数据如表2所示。

4.2 基于多工况的换热器网络结构优化

针对实际工业环境中操作工况变化的情况，本文基于多工况对HEN1进行旁路数量、旁路开度、换热器面积的优化，旨在探索换热器网络经济性与可控性之间的权衡。

4.2.1 工况1：旁路数量变化旁路是进行流股分流和温度调节的重要工具，不同的旁路数量显然将影响换热匹配进而影响换热器网络的经济性。同时，由于旁路开度是构成控制结构所必须的操纵变量，因此不同的旁路数量必然会影响换热器网络的可控性。

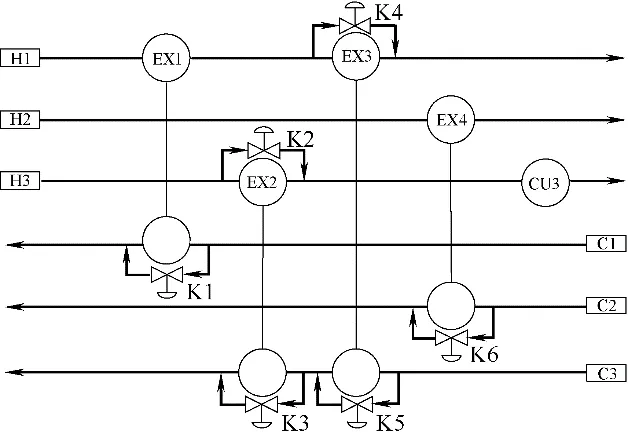
图2 HEN1结构Fig.2 Scheme of HEN1 structure

旁路数量对换热器网络的经济性和可控性的影响如图3所示。年度总费用随旁路数量的增加而增大，这是由于在流股匹配不变的情况下，旁路的存在使经过换热之后的热流股温度变得更高，或者冷流股温度变得更低，这使得最小传热温差减小，导致换热器面积相对增大，从而使投资费用增大，造成年度总费用增大。同时，随旁路数量的增加，相对增益矩阵数也呈现整体不断增大的变化规律。其原因是旁路数量越多，所构成的控制回路越多，控制回路之间的相互作用越强烈。然而，对于可控性的换热器网络，所有流股出口温度均需要被调控，故选择与流股数量相等的操纵变量。因此，该换热器网络选择6个旁路。

综上所述，当以经济性目标为导向时，换热器网络应分配较少的旁路数量；当以可控性目标为导向时，同样应该选择较少的旁路数量；但当工艺指标要求较为严苛，要求换热器网络所有流股高度可控时，则选择与被控变量数量相同的旁路。

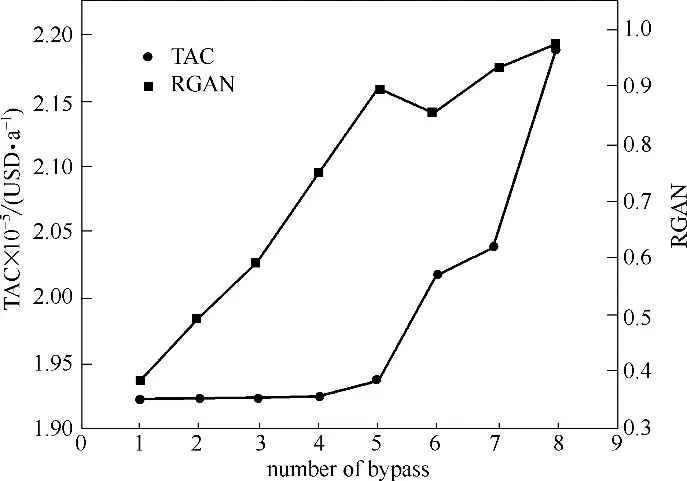
图3 旁路数量对TAC和RGAN的影响Fig.3 Effect of bypass number on TAC and RGAN

4.2.2 工况2：旁路开度变化在工业生产中，通常采用旁路开度调节的方式来实现换热器网络的控制，该方法具有自由度大、反应灵敏等优点。旁路开度不同，流经换热器的热容流率不同，导致换热器网络的最小传热温差不同，最终影响其经济性和可控性。并且不同的旁路开度调节存在相互影响，这会导致剧烈的控制回路间相互作用。本文同时对HEN1中旁路K1,K2和K3的开度作出调节，旁路开度调节上限设置为0.5[33]。旁路K1,K2 和K3 的开度变化对换热器网络年度总费用和相对增益矩阵数的影响分别如图4和图5所示。

由图可知，不同旁路开度对换热器网络经济性和可控性有不同的影响。旁路K1 和K2 的开度变化对换热器网络年度总费用有着强烈影响：其开度增大，年度总费用增大。而旁路K3 的开度变化对年度总费用的影响较小，但也呈现相同的规律。这是因为在流股匹配不变的情况下，随着旁路开度的增大，流经换热器流股的热容流率变小，而换热流股与流经旁路流股混合后的温度仍需满足换热网络整体热交换，因此被加热的换热流股温度变高，被冷却的换热流股温度变低，导致换热器面积增大，进而使得年度总费用增大。由图5 可知，相对增益矩阵数随旁路K1 和K2 开度的变化趋势一致，两者与旁路K3 协同作用于换热器网络的可控性。这是因为旁路K1 和K2 均为所在流股上的唯一旁路，受其他旁路影响较小，所以其对可控性的影响相似。然而由于换热网络的多控制回路特性，各控制回路之间有强烈的耦合作用，导致旁路开度不同对可控性有不同影响，但影响规律尚不明晰。如图所示，最小相对增益矩阵数对应于旁路K3 的开度为0.5。

表2 换热器网络对比Table 2 Comparison of HEN

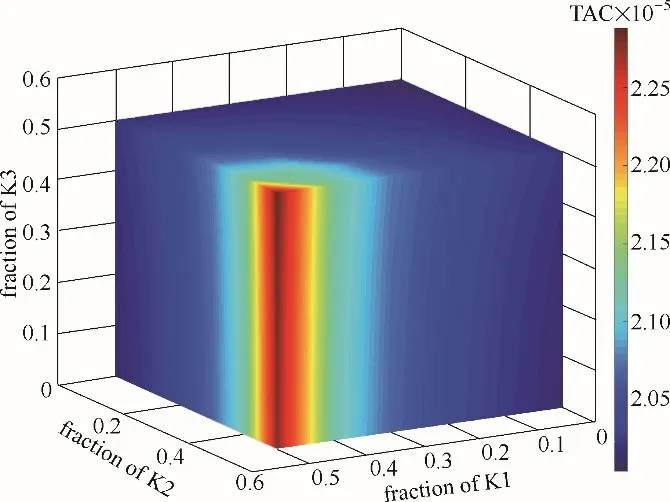
图4 TAC随旁路开度变化Fig.4 TAC variation with bypass fraction

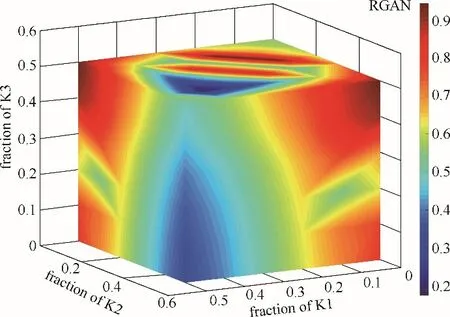
图5 RGAN随旁路开度变化Fig.5 RGAN variation with bypass fraction

综上所述，当进行旁路开度变化的工况调控时，需考虑不同旁路间相互影响，分析其变化规律以优化换热器网络结构。鉴于其相互影响尚不明朗，应优先考虑旁路的最大开度来探索换热器网络年度总费用和相对增益矩阵数间权衡。

4.2.3 工况3：旁路开度和换热器面积变化当不确定性因素存在时，通常通过调整换热器面积来抵御其干扰[34]，但这会导致旁路开度偏离其原有的最优值。因此应分析旁路开度和换热器面积同时变化的工况来优化网络结构和可控性。换热器EX2与其换热器网络中四条流股均存在关联，故分析EX2 的面积变化与旁路K3 开度变化对换热器网络的年度总费用和相对增益矩阵数的影响，结果如图6和图7所示。

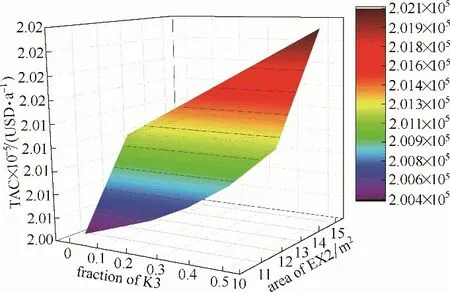
图6 TAC随旁路开度和换热器面积变化Fig.6 TAC variation with bypass fraction and HE area

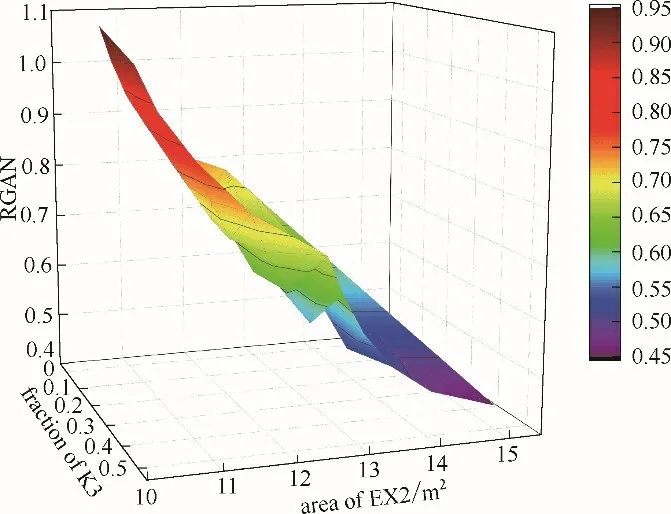
图7 RGAN随旁路开度和换热器面积变化Fig.7 RGAN variation with bypass fraction and HE area

换热器网络年度总费用随换热器EX2 面积和旁路K3开度的变化趋势一致：随面积或者开度的增大而增大。其原因是换热器EX2 面积增大导致投资费用增加。同时根据工况2 的分析，旁路K3 开度增大带来换热器网络最小传热温差的增大，导致年度总费用不理想。而相对增益矩阵数的变化趋势与换热器网络年度总费用相反。随着换热器EX2面积和旁路K3开度的增大，其呈现略有波动但整体变小的趋势，与工况2的优化结果相符。

综上所述，当以经济性目标为导向时，应优先选择较小的换热器面积和旁路开度；当以可控性目标为导向时，应优先选取较大的换热器面积和旁路开度。

根据以上不同工况的分析，权衡换热器网络的经济性和可控性，得到优化的换热器网络结构，标记为HEN2，旁路K2 开度为0.2，K3 开度为0.5，其余旁路开度为0.1，各换热面积如表2所示。

4.3 基于可行性分析的换热器网络结构与控制结构改造

可行性分析是检验换热器网络在实际操作中能否正常运行的有效手段。因此，计算换热器网络HEN2 的柔性指数，得到结果为0.687，表明其无法抵御不确定性因素的干扰。

辨识HEN2的临界操作点并在其上进行换热器网络结构和控制结构的改造，得到能够抵御扰动变化的换热器网络，标记为HEN3，如图8所示，相关数据如表2 所示。计算HEN3 柔性指数，其结果大于1，表明HEN3 满足操作可行性需求。同时，其可控性相比于HEN1提高了28.25%。

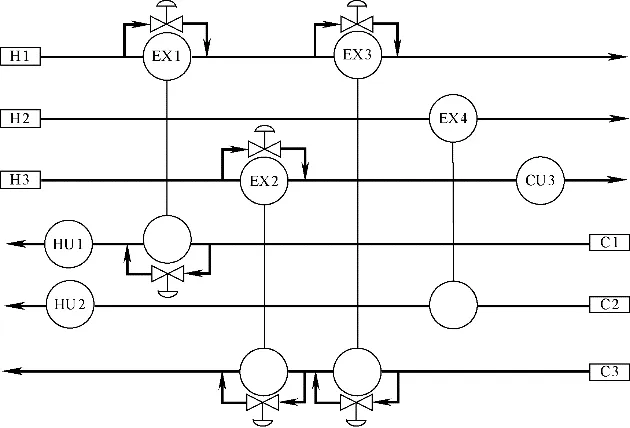
图8 HEN3结构Fig.8 Scheme of HEN3 structure

4.4 传统换热器网络综合结果对比

另外，引入传统换热器网络综合结果与本文所得结果进行对比，进一步说明本文所提方法的可行性与有效性。传统换热器网络综合结果如图9 所示，标记为HEN4，其相关数据见表2。可知，相比于HEN4，HEN1、HEN2和HEN3均具有优越的可控性。且HEN3 能抵御不确定性因素的干扰，其可控性相比HEN4提高了69.86%。

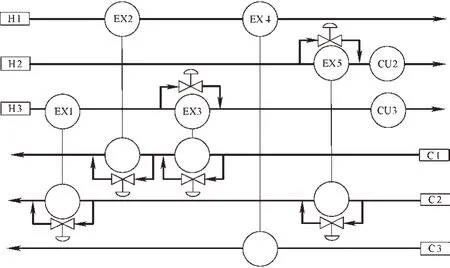
图9 HEN4结构Fig.9 Scheme of HEN4 structure

5 结论

本文充分考虑了换热器网络结构与可控性的相互作用关系，提出了可控性换热器网络综合方法，并基于多工况探究了决策变量对网络结构的影响，进而对其进行优化。同时，在不确定性因素下对换热器网络进行可行性分析，通过优化换热器面积，保证换热器网络的操作可行性，且改善换热器网络的可控性。通过实例分析，所得结果权衡了换热器网络的经济性和可控性，且其柔性指数大于1，保证换热器网络的操作可行性，证明了该方法的可行性及有效性。

符号说明

A——换热器面积，m2

C——换热器面积费用指前因子

Ccu——冷公用工程单位费用，USD·kW-1·a-1

Chu——热公用工程单位费用，USD·kW-1·a-1

CF——换热单元的固定安装费用，USD·a-1

d——设计变量向量

h——单侧流股的传热膜系数，kW·m-2·K-1

NK——超结构级数

q——换热单元热负荷，kW

Ti,NK——热流股出口温度

Tj,1——冷流股出口温度