闭式喷雾冷却的瞬态传热过程研究
2020-05-15周年勇徐慕豪冯浩段锋王庆荣陈海飞郭强
周年勇,徐慕豪,冯浩,段锋,王庆荣,陈海飞,郭强
(常州大学石油工程学院,江苏常州213000)
引 言
喷雾冷却通过高压将工质雾化成细小液滴喷射到热沉表面,具有传热温差需求小、工质需求少、热通量高及冷却均匀等优点,目前已广泛应用于国防、微电子、冶金、机械加工、医疗、航空航天等领域[1-3]。实际工程应用领域中,冶金、机械加工等应用方向通常散热量较为稳定,需要较长时间的均匀冷却,相关的稳态喷雾冷却研究较为成熟。而医疗、国防及航空航天方向的散热量变化较大,需要灵活高效的瞬态冷却,但相应的瞬态喷雾冷却研究相对匮乏。
喷雾冷却属于复杂的多相流问题,其传热机理研究还存在着一些争议。国内外学者根据各自实验工况总结出大量传热关联式,Cabrera[4]以水为工质研究了液滴粒径、速度、环境压力、表面粗糙度等影响因素对热通量的影响,并建立描述核态沸腾区与临界热通量CHF 的经验模式。Rybicki 等[5]使用PF-5052 进行工质向上冲击的实验,并联合向下定向的FC-72、FC-47 实验数据,证明了先前用于向下定向喷雾的CHF相关性同样适用于向上的PF-5052工质。王锐等[6]通过降低制冷剂R1234yf 过热度的方式,有效提高喷雾集中程度,在保证闪蒸雾化的前提下显著提高表面热通量。稳态喷雾冷却过程中,学者们广泛关注工质种类、工质流量[7]、喷嘴类型[8-9]、表面粗糙度[10-11]等影响因素对喷雾冷却性能的影响,其中,喷雾流量[12-13]是影响喷雾冷却性能的重要因素,流体改性是近年来喷雾冷却研究的热点。Cui 等[14]、Wang 等[15]研究表明表面活性剂及低浓度的可电离介质可以增强换热性能,而醇类等非电离介质则会降低换热性能。另外,刘红等[16]利用添加不同浓度低醇类添加剂,发现去离子水中加入乙醇和正丁醇,存在强化换热的最佳添加剂浓度。
喷雾冷却的瞬态传热过程复杂多变,且跨越多个传热区间。部分学者探究了适用于喷雾冷却表面瞬态传热适用的计算方法。余宁等[17]研究了非傅里叶导热定律在瞬态条件下的温度分布,并指出其热效应跟热作用时间与材料弛豫时间的比值相关。周致富等[18-20]对比分析了Duhamel定理、顺序函数法与格林函数法在不同测温方法下计算表面热通量的有效性和适用性,并进一步研究了不同工质下瞬态喷雾冷却传热特性,总结出相关制冷剂的相变传热通用关联式。Xu 等[21]在考虑冷却基体热容的情况下,得出表面温度间接测量情况下的传热计算公式。Hsieh 等[22]使用瞬态液晶技术和热电偶丝进行表面温度测量,确定了质量流量、Weber数和过冷度对R134a 瞬态喷雾冷却过程的影响。Baysinger 等[23]在微重力和高重力环境下进行瞬态喷雾冷却实验,并建立瞬态分析模型来预测受热区域的表面温度及传热系数。Cader 等[24]比较了喷雾冷却及传统风冷冷却瞬态模具功耗的能力,在同样条件下,喷雾冷却不仅能快速完成冷却目的,且耗能较少。Zhou等[25-26]在R410a喷雾冷却系统中,发现表面翅片型式以及喷雾距离和喷嘴直径对闪蒸系统中传热性能有极大的影响。Wang 等[27]构建了新型的喷雾腔结构,研究了常规喷雾冷却(SC)、浸没式喷雾冷却(ISC)及池沸腾3 种冷却模式下的传热性能,研究指出浸没式喷雾冷却的传热性能最佳,这是因为浸没条件下表面蒸气膜层被消除,且在热源表面周围形成强烈紊流造成的。
学者们在喷雾冷却特性研究方面取得了丰富的成果,并总结了相应的传热关联式,但关联式中影响因素繁多,只适用于特定工况下的喷雾冷却。此外,学者们的研究成果集中于稳态喷雾冷却的某一传热区域,而不是研究整个喷雾冷却过程,对于喷雾冷却瞬态传热的研究相对较少。本文搭建了闭式循环喷雾冷却实验台,研究不同工况下的喷雾冷却的瞬态传热过程,分析各个区域的传热特性,为喷雾冷却推广应用提供实验及理论支撑。
1 实验系统
实验装置如图1 所示,闭式循环喷雾冷却实验台主要由四个部分组成,分别是喷雾腔、加热系统、供液系统、测控系统,其工作原理为:制冷剂气体从气液分离器中流出,经压缩机压缩后进入预冷器初步冷却,冷却后进入冷凝器冷凝至过冷液态。过冷工质再经流量计由喷嘴喷射至加热表面处。换热结束后的工质流入预冷器升温,确保管内制冷剂为气态,最后进入水冷器降低压缩机入口温度后流入压缩机,如此重复循环。
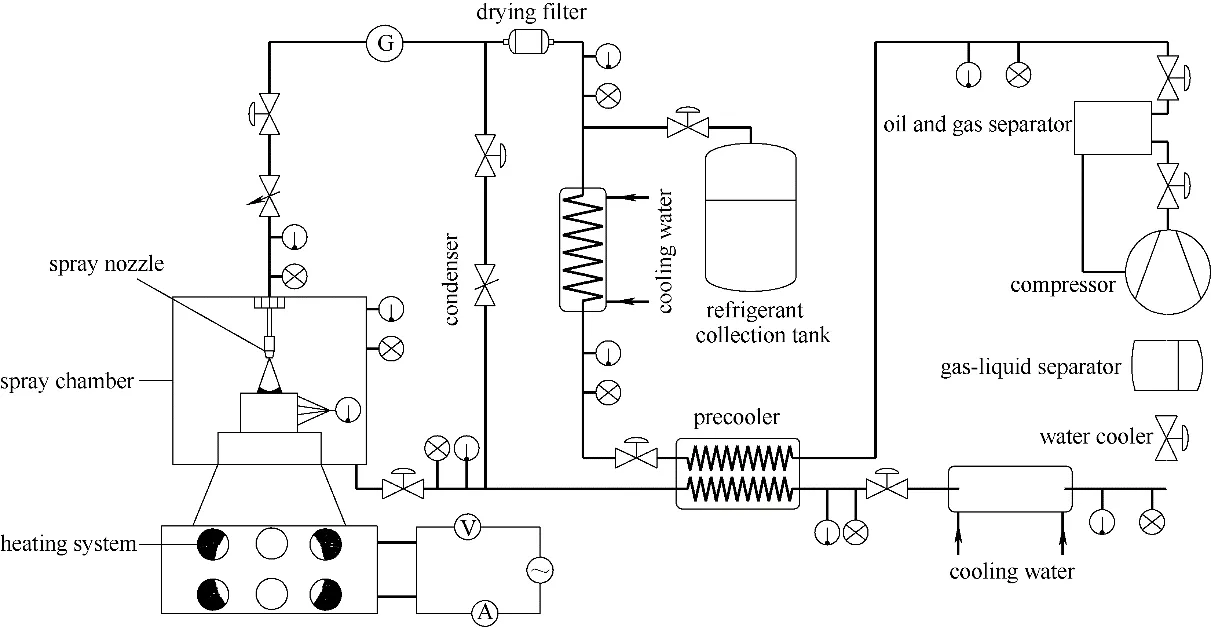
图1 闭式循环喷雾冷却实验系统原理图Fig.1 Schematic diagram of closed loop spray cooling experimental system
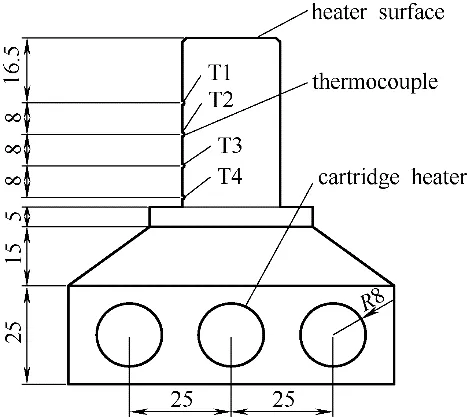
图2 模拟热源结构Fig.2 Structure of simulation heat source
模拟热源如图2 所示,由上表面直径为24 mm的紫铜元件和3 根功率为500 W 的加热棒组成,通过调节电压控制模拟热源的加热量,加热块周围填充硅酸铝纤维棉,紫铜棒上端与胶木板接触处涂有密封胶并设置“O”形圈以达密封和绝热的目的。在距热沉表面16.5、24.5、32.5 及40.5 mm 位置安装K型热电偶。喷嘴型号为美国斯普瑞公司的1/8GGSS1.5,调整喷雾高度为60 mm;加热器控制加热功率范围0~1500 W,配置PW9901 智能参数测量仪读取监控电功率、电流等参数。
2 数据处理与误差分析
喷雾冷却传热性的优劣由三个重要参数:热通量q、被冷却表面温度Tw和表面传热系数h 来衡量。对于非稳态过程,不能直接用傅里叶导热定律求解,需要考虑铜块本身热容的影响,又由于实验热源颈部圆柱体满足一维导热的特性,且热导率为常数、无内热源,对于一维非稳态导热微分方程,简化求解,热通量可以表述为
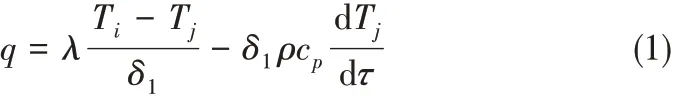
其中λ 为铜的热导率,Ti和Tj是不同位置热电偶所测温度,δ1是i和j相应位置热电偶之间的距离,ρ是铜的密度,cp是铜的比热容。
为了验证实验热源一维导热假设的准确性,采用Fluent 软件进行仿真计算,计算时加热量为625 W,表面传热系数为4 W/(cm2·K),其他外壁为绝热面。由图3 可知,实验热源温度分布云图具备良好的线性,为了进一步验证一维导热假设的准确性,对圆柱颈部选取系列点进行一阶线性拟合,拟合公式为y = -0.71099x + 337.02735,拟合度因子R2达0.99995。综上,实验热源的一维导热假设成立。
则喷雾冷却表面温度计算式为

式中,Tw是被冷却面表面温度;δ2是j 位置热电偶与冷却表面之间的距离。
导热反问题法[28-30]常用于瞬态传热计算中,但是对于多工况,大数据条件下,往往数据处理效率较低,且过程求解复杂。为了进一步验证式(1)与式(2)的适用性,对论文中的典型工况,运用导热反问题法求解冷却表面温度,并与本文公式的求解结果进行对比。
如图4 所示,本文数据处理方法与导热反问题法求解相比,温度变化趋势也基本一致,且相对误差在允许范围内,在多工况、大数据条件下,运用本文求解方法,可极大地提高数据处理效率,能够准确反映传热过程的变化趋势。
实验中所涉及的测量仪器及其精度如表1所示。
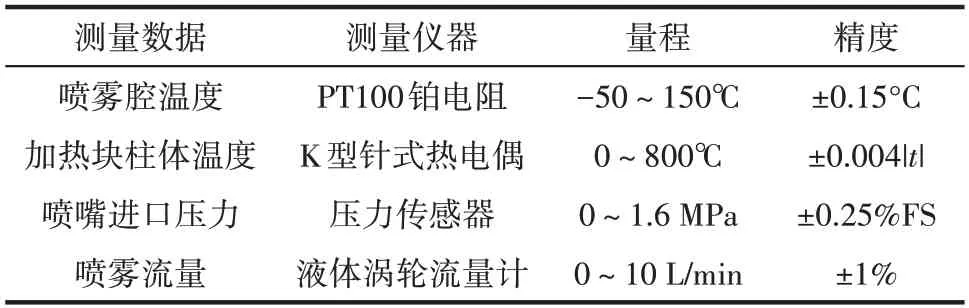
表1 测量仪器及其精度Table 1 Measuring instruments and precision
根据误差传递公式[23],计算得实验中热通量、加热表面温度和综合传热系数的不确定度分别为±5.6%、±2.9%、±5.4%。
3 实验结果与分析
3.1 初始表面温度对喷雾冷却瞬态过程的影响
选取R134a 为制冷工质,探究闭式循环下不同初始冷却表面温度对喷雾冷却瞬态传热过程的影响。实验过程中,加热功率恒定200 W,待冷却表面温度加热到设定温度后,开启喷雾冷却装置,对热表面进行冷却,喷雾流量为0.20 L/min,观测表面温度变化并记录实验数据。改变冷却表面初始设定温度,重复实验。
图5、图6显示了不同初始表面温度T0下的热通量和表面温度变化曲线,实验设定的初始温度T0分别为65、80、95、110、125、135、140 和155℃。随着初始温度的增加,喷雾冷却瞬态过程呈现两种不同变化规律,可将之标注为模式Ⅰ(1a-1b-1c-1d)和模式Ⅱ(2a-2b-2c)。当初始温度T0≤135℃时,热通量先缓慢上升,再快速上升至最大值,最后下降至平衡值,而表面温度先缓慢下降,再快速下降,最后接近稳定,其冷却稳定温度低于20℃;当初始温度≥140℃时,热通量逐渐线性上升,并在达到某点保持这个热通量,而表面温度先缓慢下降至最低点后,再逐渐上升。
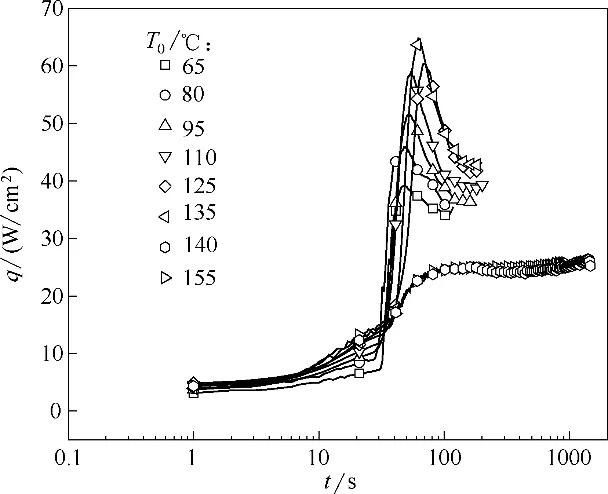
图5 不同初始温度下热通量变化曲线Fig.5 Curves of heat flux density at different initial temperatures
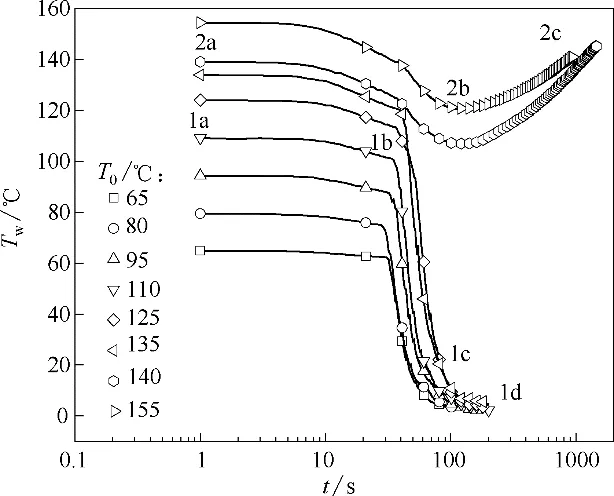
图6 不同初始温度下表面温度变化曲线Fig.6 Curves of surface temperature at different initial temperatures
随着表面初始冷却温度的增大,模式Ⅰ的喷雾冷却传热过程中在喷雾初期启动影响后,开始迅速进入急速增长阶段,且开始急速增长的时间相差不大,整个增长过程斜率一致。当喷雾冷却传热过程中温度变化呈现出模式Ⅱ时,热通量在启动初期影响后很快就快速增长到一个值,并维持很长一段时间,初始冷却温度的增加并没有给热通量曲线带来明显影响。
由图7 可知,对于模式Ⅰ表现为1a-1b-1c-1d的喷雾冷却瞬态过程,当冷却过程处于1a-1b时,是冷却系统刚启动阶段,加热表面尚未形成相对稳定的蒸汽膜层,且随着出液量的逐渐增大,有个短时间的冷却能力增强,该过程持续时间大约在60 s内,称为启动初期效应。当冷却过程处于1b-1c 时,喷雾冷却处于过渡沸腾区,为了趋向于稳定过程,表面温度下降,热通量q先增大后减小,传热过程越过临界热通量点(CHF),由过渡沸腾区转向核态沸腾区。1c-1d 便是喷雾冷却在核态沸腾区逐渐趋向于平衡的过程,此时加热系统提供的热量近似等于冷却系统从表面带走的热量,整个过程属于准稳态过程。
对于模式Ⅱ2a-2b-2c 喷雾冷却瞬态过程,当冷却过程处于2a-2b 时,其温度及热通量的变化规律也是启动初期效应造成的;当冷却过程处于2b-2c时,热通量曲线并没有如模式Ⅰ一样先增大后减小,而是结束喷雾冷却的瞬态响应后,热通量先逐渐增加至莱登弗罗斯特点(LFP),再缓慢升高至平衡点,但表面温度先略有降低,再不断上升,最终在膜态沸腾区的某点达到平衡状态,但由于实验台安全限制,本次实验并未完全达到膜态沸腾区的平衡点。
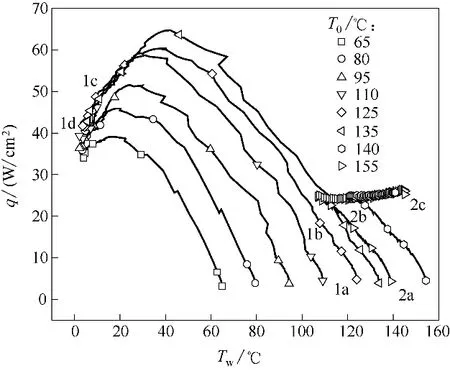
图7 不同初始表面温度下瞬态喷雾冷却的沸腾曲线Fig.7 Boiling curves of transient spray cooling at different initial surface temperatures
3.2 恒定热源功率对喷雾冷却瞬态传热过程的影响
为了探究恒定热源功率对喷雾冷却瞬态传热过程的影响,实验中选取工质仍为R134a,初始表面温度T0=150℃,加热功率分别为100、200 和400 W。如图8所示,随着恒定热源功率的降低,表面温度变化还存在模式Ⅲ(3a-3b-3c-3d-3e),当加热功率为100 W 时,在3a-3b 之间表面温度较快线性下降,3b-3c之间缓慢线性下降,3c-3d之间急速降温,3d-3e 保持相对稳定的温度。对于模式Ⅲ,恒定热源的瞬态喷雾冷却与无内热源的喷雾冷却传热过程相似,有两个下降阶段,且中间存在一个温度缓慢下降的阶段。当加热功率较大时,且初始冷却温度较高时,表面温度变化过程都呈现出模式Ⅱ,即在膜态沸腾区的某点实现热平衡,且加热功率越大表面温度上升速率越快。
图9 展现了不同加热功率下的沸腾曲线,对于模式Ⅲ,在3a-3b过程中,热通量随着表面温度的降低而升高,同样是启动初期的增强效应造成的;在3b-3c 过程中,热通量几乎没有变化,表面温度也是缓慢下降,处于类平衡态,这是由于较低的加热功率使得传热过程在过渡沸腾区找到了热平衡点,但由于过渡沸腾区的传热机理比较复杂,稍有变动平衡就会被打破,出现了3c-3d的过程,传热过程需要越过CHF 点,在核态沸腾区找到较为稳定的平衡点,且此过程发展速率极快;在3d-3e 过程中,表面温度有所下降,但会渐渐稳定在一点,该点对应热通量便是此过程的平衡点。
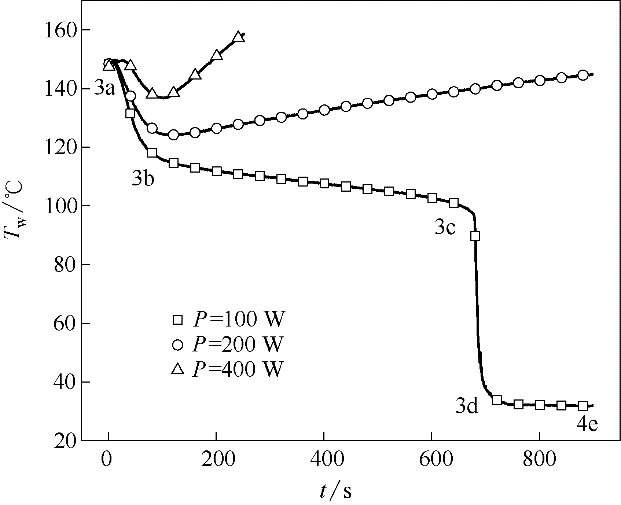
图8 不同加热功率下表面温度变化曲线Fig.8 Curves of surface temperature at different heat power
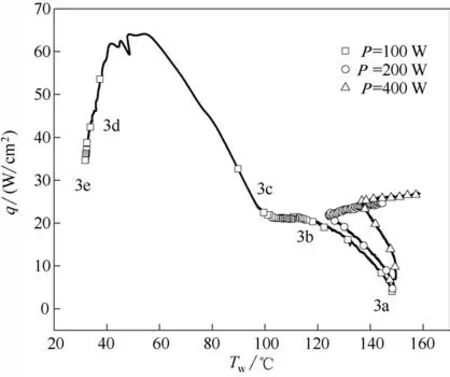
图9 不同加热功率下瞬态喷雾冷却的沸腾曲线Fig.9 Boiling curves of transient spray cooling at different heating power
3.3 不同类型工质对喷雾冷却瞬态过程的影响
保持加热功率为P=400 W,初始温度T0=150℃,对比R134a、R22与R410a三种工质下的喷雾冷却瞬态传热过程。如图10 所示,在初始温度T0=150℃时,三种制冷工质的温度变化过程表现为模式Ⅰ和模式Ⅱ,R22 和R134a 制冷剂在表面初始温度T0=150℃时纷纷出现了传热劣化,温度在一段时间的缓慢下降后逐渐上升,而R410a 表现出卓越的冷却能力,并没有传热劣化,也没有出现模式Ⅲ中传热缓慢阶段。
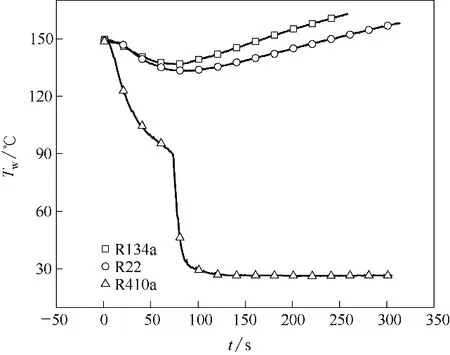
图10 不同类型工质下表面温度变化曲线Fig.10 Curves of surface temperature at different refrigerants
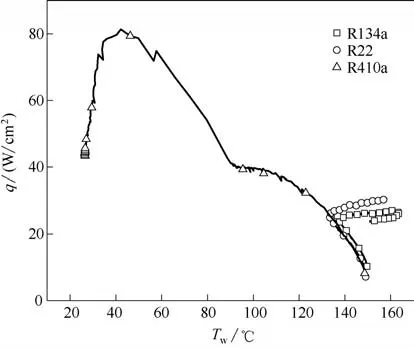
图11 不同类型工质下瞬态喷雾冷却的沸腾曲线Fig.11 Boiling curves of transient spray cooling at different refrigerants
对于不同工质的喷雾冷却瞬态传热能力差异主要在于:当在同一系统中保持设备开度不变的前提下,R410a的喷嘴入口压力为18×105Pa,饱和压力为8×105Pa,同比之下,R410a 的运行压力最高,R22与R134a 相当,这就意味着系统采用R410a 为工质拥有更好的雾化效果及较高的饱和温度,那么同等条件下,R410a 的瞬态沸腾曲线中莱登弗罗斯特点(LFP)对应的温度Tf最高。图11为三种制冷工质在T0=150℃时的沸腾曲线,R22、R134a 在冷却系统启动初期都有一个短时间的热通量升高及温度下降过程,当表面温度下降至135℃时,传热过程仍然处于膜态沸腾区,由于加热通量大于喷雾冷却从热沉表面移除的热量,且膜态沸腾区传热性能大幅下降,为了达到平衡态,表面温度开始不断上升。而R410a 制冷工质在喷雾冷却初期效应后,表面温度下降低于到LFP 对应的温度,所以整个传热过程进入过渡沸腾区,热通量需要跨越过渡沸腾区,并在核态沸腾区内达到平衡。
3.4 喷雾冷却瞬态传热过程的机理分析
喷雾冷却的沸腾曲线与池沸腾曲线相似,如图12 所示,q0对应的是喷雾冷却从热沉表面移除的热量与加热系统提供的热量达到平衡时的热通量。当q0位于临界热通量CHF及莱登弗罗斯特点LFP之间时,理论上喷雾冷却的瞬态传热过程可以在核态沸腾区、过渡沸腾区及膜态沸腾区的三个位置实现热平衡。不同的冷却初始表面温度,主要决定着在经历喷雾冷却启动初期效应后,表面温度是否小于LFP 对应的温度Tf,若是冷却初始表面温度较低,启动初期效应后温度小于Tf,则喷雾冷却进入过渡沸腾区,热通量增大,温度变化过程呈现出模式Ⅰ或者模式Ⅲ,恒定加热功率越大,传热过程越容易向模式Ⅰ发展,直接急速冷却到核态沸腾区某点平衡。反之,恒定加热功率越小,越容易在过渡沸腾区实现一段时间内的热平衡,即传热过程如模式Ⅲ,但平衡态随着时间的推移会被打破,最终在核态沸腾区实现平衡;若是表面初始温度较高,经历启动初期效应后温度大于Tf,喷雾冷却停留在膜态沸腾区,表面温度会出现模式Ⅱ,表面温度升高,传热过程在膜态沸腾区某点实现热平衡。因此,初始表面温度的高低决定了传热过程的走向,但恒定加热功率的大小决定了表面温度的上升或者下降的速率;另外,同等条件下,对于不同类型介质,喷嘴入口压力及饱和温度越高,其Tf也越高。
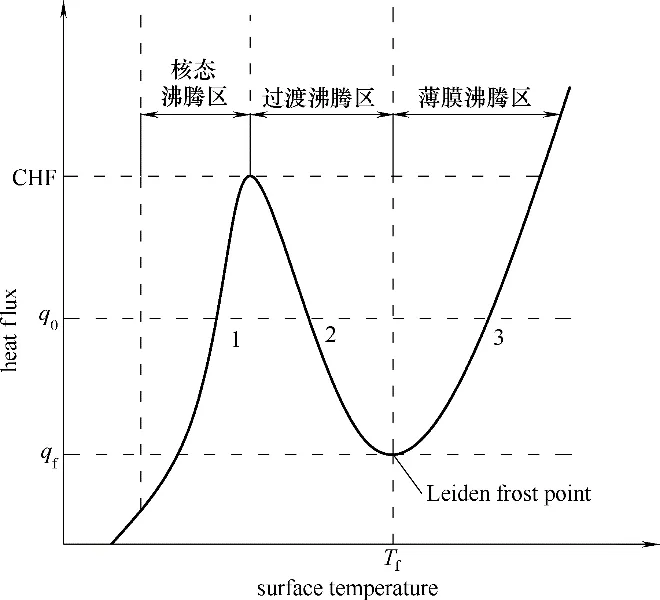
图12 喷雾冷却沸腾曲线Fig.12 Boiling curve of spray cooling
4 结 论
本文搭建了闭式喷雾冷却实验台,实验研究了喷雾冷却的瞬态传热过程,建立了准确描述其传热过程的实验曲线,分析了冷却初始温度、加热功率及工质类型对瞬态传热过程的影响,具体结论如下。
(1)对于喷雾冷却的瞬态传热过程,其表面温度变化趋势可分为3类:模式Ⅰ,表面温度直接急速冷却到核态沸腾区某点平衡;模式Ⅱ,表面温度不断升高,并在膜态沸腾区某点实现热平衡;模式Ⅲ,表面温度先在过渡沸腾区实现一段时间内的热平衡,但平衡态随着时间的推移会被打破,最终在核态沸腾区实现平衡。
(2)在闭式系统启动初期,喷雾冷却的瞬态传热过程有个短时间的冷却能力增强阶段,初始表面温度在经历启动初期效应后,若小于莱登弗罗斯特点(LFP)对应的温度Tf,则表面温度不断下降,在核态沸腾区实现热平衡;反之,表面温度升高,在膜态沸腾区实现热平衡。
(3)对于喷雾冷却的瞬态传热过程,恒定加热功率的大小决定了表面温度变化速率,随着恒定加热功率的增大,表面温度下降或者上升的速率加快;另外,同等条件下,对于不同类型介质,喷嘴入口压力及饱和温度越高,其莱登弗罗斯特点(LFP)对应的温度Tf也越高。
符 号 说 明
cp——铜的比热容,J/(kg·℃)
h——表面传热系数,W/(㎡·℃)
p——进出口压力,Pa
q——热通量,J/(㎡·s)
Tf——莱登弗罗斯特点对应温度,℃
Ti,Tj——不同位置热电偶所测温度,℃
Tw——被冷却面表面温度,℃
ρ——铜的密度,kg/m³
λ——铜的热导率,W/(m·℃)
δ1——i和j相应位置热电偶之间距离,m
δ2——j位置热电偶与冷却表面之间的距离,m
