动态结冰孔隙结构三维建模方法

李伟斌，宋超，易贤，马洪林，杜雁霞

（1 中国空气动力研究与发展中心计算空气动力研究所，四川绵阳621000； 2 中国空气动力研究与发展中心飞行器结冰与防除冰重点实验室，四川绵阳621000）

引 言

动态结冰是指结冰所需的液态水由气流输运而来，并在液态水运动撞击基底的过程中不断冻结而动态形成的。相比于静态结冰，正是由于这一“动态”特点，使得在冻结过程中，水膜与冰层间的空气以及部分水滴中的空气来不及逃逸，被“囚困”于结冰中，形成内部孔隙结构[1]。这种孔隙结构特征决定了结冰的许多重要物理性质，比如密度、热传导能力、强度等[2-4]。动态结冰的这一孔隙结构因结冰条件的不同而具有可见的差异，快速获取动态结冰孔隙结构定量信息是根本上认识其动态形成过程的内在机制，也是结冰热/力学相关方向研究的基础[5]。

目前关于结冰微观特性的研究多集中于数值模拟。在结冰生长微观研究方面，动态结冰被认为主要包括晶核的形成和晶体生长两个阶段[6]，其中第一阶段是过冷水滴热力学非平衡态到平衡态转变的过程[7]；第二阶段是液/固界面推进直至完全凝固的过程[8-9]。在飞机结冰中，第一阶段明显快于第二阶段[10]，这也导致了早期飞机结冰研究忽略形核这一重要现象。同时，应用分子动力模拟结冰的全过程也迅速发展[11-12]，表明形核是足够数量的氢键结合从而形成第一阶段的初始核，进而受热力学行为影响，初始核改变形状和大小，快速生长直至最终的全结晶。在基底表面接触结冰方面，针对不同表面、不同粗糙度的接触表面，现有研究从分子和纳米尺度，对形核开展了数值模拟，结果表明相对于光滑表面，粗糙表面不易形核[13]；同样地，曲率大的表面也会减少形核速率[14-16]。这一点在结合电子显微成像系统开展的超疏水材料涂层实验中得到了验证[17]，因为这种材料被认为是在原有基底表面形成了一层微纳米粗糙的特征，从而延缓了形核冻结的时间。正因为如此，超疏水材料对于减小结冰表面的黏附作用具有重大贡献[18-19]。另外，大水滴静止结冰[20]和碰撞结冰[21-22]的热力学和动力学行为也得到了研究，表明过冷态温度越大、水滴尺度越小或接触面温度越低，水滴的相变速率越高；提高表面疏水性，不仅能够减小水滴碰撞后的铺展湿润面积，而且能够缩短水滴同壁面的接触时间，从而降低水滴内部的相变速率，这点也在大水滴结冰实验中得到了较好的验证[23]。

现有针对动态结冰微观特性的实验研究和模拟研究已经较多，研究表明影响动态结冰微观结构的结冰条件主要有速度、温度、粒径、液态水含量等，其中温度越低，孔径最大值越大，孔隙率越大[3]；速度越高，来流对气泡的粉碎作用越强，因而气泡体积也相对越小，孔隙率越小[24]。这些研究对结冰微观特性有了一定的定性理解，然而缺少类似多孔材料的细致定量研究。在二维孔隙率分析方面，主要做法是低温环境下获取结冰的截面显微图像，进而进行相关分析讨论[3,24]。在多孔材料孔隙结构定量信息提取研究领域，目前较为有效的途径是通过建立三维模型进行定量分析，具体做法是利用CT 或者Micro-CT 获取对象的二维序列图像，并对其进行图像处理，再进行三维重建，结果可视化软件包括OpenGL、Matlab、Tecplot 等，相关研究已经遍历土壤学[25-26]、材料学[27-28]、医学[29-31]等。然而由于动态结冰的材料特点，并不能进行相同的扫描建模，因此，其定量信息的提取是动态结冰的难点问题之一[32]。

动态结冰孔隙结构相关研究已经取得了一定的定量信息，然而对于结冰的三维模型建立以及三维信息定量提取方面，缺少必要的研究手段及方法。本文针对动态结冰孔隙结构三维建模问题，基于结冰孔隙形状、孔径、分布等二维图像定量信息，在合理假设的基础上，研究孔隙的定位及定量方法，探索孔隙模型的量化表征及显示方法，并验证方法的可靠性。以期为动态结冰三维刻画以及特征参数的表征提供新途径。

1 动态结冰孔隙分布的基本假设

动态结冰具有孔隙结构，宏观上表现为图1 的不透明状，微观上含有大量气泡孔隙。李伟斌等[3]在中国空气动力研究与发展中心0.3 m×0.2 m 的结冰风洞中开展了结冰实验，并使用Olympus CX31型显微镜获取结冰微观图像，采用图像分割的方法提取结冰微观图像中的二维定量信息。基于此，文章从微观角度入手，通过对不同结冰条件下的结冰、同一实验状态不同位置结冰的定量分析，最终得到了动态结冰如下的定量分析结果。

图1 具有气泡的动态结冰Fig.1 Dynamic icing with pores

(1) 孔隙呈球形。利用圆形度表征量[33]对孔隙截面进行统计分析，该值大于0.7854(正方形)的区域占比较大，结合显微图像采集的广泛性及随机性，可以推广得到孔隙任意截面均为圆形、结冰孔隙为球形的结论。

(2)孔隙直径取值是连续的。统计大量孔径数据，得出其可以取一定范围内的任意值。并且理论上，在结冰过程中，主要受结冰热力学的影响，孔隙的形成具有一定随机性，其半径可以为任意实数。因此，孔隙孔径的取值是连续的。

(3)孔隙直径服从特定分布。文献[3]中所使用的显微镜在40倍放大率，对不同结冰状态下的结冰直径分布进行曲线拟合，其服从式(1)的特定分布。

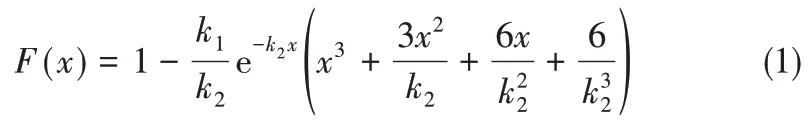
其中，x ∈[0,+ ∞)，k1、k2均为正实数，不同来流条件下结冰微观孔隙的直径分布对应不同的k1和k2。

(4)孔隙分布位置的随机性。孔隙的形成过程受结冰条件和热力学的影响，虽然呈现一定规律，但具有较强的随机性。

本文以此作为结冰三维孔隙结构建模的假设，该假设是本文建模方法的重要基础。

2 动态结冰微观结构的三维建模方法

为更直观重建结冰内部孔隙结构，将结冰微观结构抽象化三维矩阵的形式，基于随机的形式和孔径分布函数式(1)确定矩阵各坐标点处的取值，其中以0表示结冰，1表示结冰内部的孔隙。三维建模是问题数学化过程，表示为求刻画结冰微观结构的矩阵T:Ω →{0,1}，其中Ω ⊂Z3，其求解过程如图2 所示。建模过程主要分为五个步骤：①确定需要生成的结冰的大小(尺寸)；②根据实验采集到的结冰二维微观图像，测量其孔隙率，进而确定三维建模时孔隙的数量N；③根据第1 节中结论(4)随机生成N个孔隙的位置信息；④根据第1节中结论(3)，生成服从分布式(1)的孔隙直径信息；⑤最终基于以上步骤生成结冰微观结构，并予以显示。这五步对应的详细过程见2.1～2.5节。

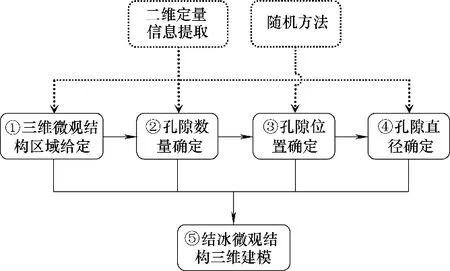
图2 三维建模方法流程Fig.2 Flow diagram of 3-D modeling method

2.1 三维微观结构的区域

给定区域Ω =[1,I]×[1,J]×[1,K],Ω ⊂R3，并令T(Ω) = 0，即以大小为I × J × K 的三维0-矩阵(矩阵元素值均为0)T表示待确定的结冰三维微观结构区域，该矩阵也可视为是三维图像。

在微观结构确定的基础上，必须给定矩阵大小与实际结冰尺寸的变换关系。将矩阵元素的坐标与长度间建立关系，两个元素间距离为1，记为1 像素，建模中以比例r(像素/毫米)表示，即r个矩阵元素长度对应真实结冰的1 mm。比例尺r可以由结冰二维显微图像中的标定结果确定。如果需要获取更精细化的三维微观结构，可以增大r。

2.2 区域内孔隙数量

动态结冰内部由一定数量的孔隙组成，记其数量为N。孔隙分布具有随机性，又具有一定的规律性，基于此文中假设三维每个界面的孔隙分布是相同的。那么，三维的孔隙体积占比就等于二维的孔隙面积占比λ2D，称它们为孔隙率[34]，并以此作为三维建模的数量特征，数量N的确定方式基于式(2)

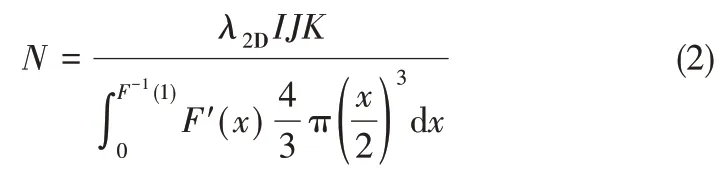
式中，F-1(1)为式(1)分布函数逆函数在1处的取值；F'(x)为分布函数的导数，即概率密度函数。

由于在计算二维孔隙率时，并未考虑孔隙交融的情况，而在三维孔隙结构建模时会存在这种现象。因此，在建模时需要考虑这点带来的三维体积损失和二维面积损失，经过多次建模实验，文中经验性地选取3%进行修正补偿，即

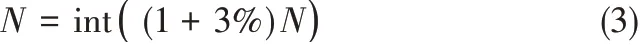
式中，int()表示求整运算。

2.3 孔隙位置

基于孔隙为球形的假设，孔隙的位置可以由球心位置确定。本文球心坐标以随机的形式确定，记其为Oi(xi,yi,zi),i = 1,…,N。

在区间[1，I×J×K]上以均匀分布方式生成N 个随机实数{Xi|i = 1,2,…,N}，以式(4)生成孔隙的球心坐标。

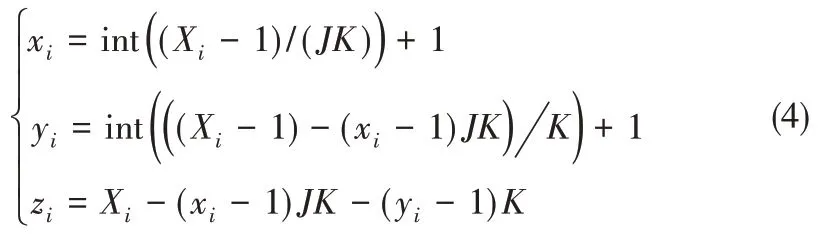
2.4 孔径分布

由式(1)孔隙直径分布可以直接得到孔隙率，而孔隙率决定了结冰的密度、致密程度及其热力学特性等，是决定结冰宏观特性的主要和关键因素，是关乎防除冰策略优化的重要因子。因此，获取准确的孔径分布(孔隙率)是建立结冰微观结构三维模型的关键步骤，是开展后续研究的前提。

建模中采用的孔径分布由式(1)得到，而其中的参数k1和k2由二维图像中得到，具体做法是在低温环境下制作结冰的切片，在显微镜下获取结冰微观图像，进而采用图像分割的方法获取孔隙部分，采用Matlab 自带命令得到各孔隙的周长和面积，进而以孔隙呈球形的假设得到其直径，最后根据多个孔隙直径信息确定式(1)中的两个参数k1和k2。

式(1)是特定实验条件下提取的分布公式，需在其基础上转化为本文的孔径d，转换为式(5)

式中，η(像素/毫米)是结冰显微图像中像素与真实尺寸之间的比例尺。

具体地，按照均匀分布规则，在区间(0,1)上生成N 个随机数{Yi|i = 1,2,…,N}，并求出分布函数式(1)所对应的逆{F-1(Yi)|i = 1,2,…,N}，则本文的孔隙直径为

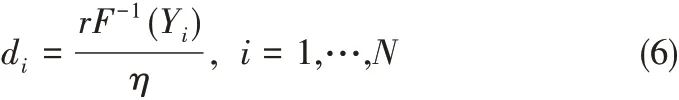
2.5 三维微观孔隙结构

更新零矩阵T，生成动态结冰三维微观孔隙结构，其对应值为1。

以{(Oi,di)}(i = 1,…,N)为对，依次对矩阵中的元素取值进行更新。令

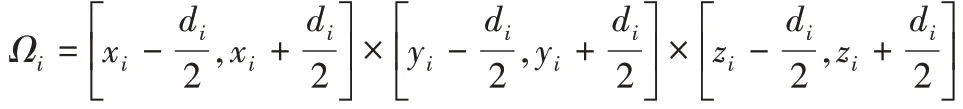
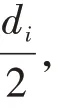
3 建模结果及可靠性分析

以实验状态粒径MVD=38 μm，液态水含量LWC=0.75 g/m3，v=25 m/s，T=-6℃下的结冰二维显微图像为例，构造其对应的三维微观结构。程序在Matlab 7.6中编写，PC配置为8核CPU 3.4 GHz，内存为16 GB。

3.1 二维定量信息

图3(a)是该状态下的显微图像，大小为382×288，其与真实尺寸之间的比例尺η ≈27(像素/毫米)。图3(b)是变分分割方法的分割结果。图4 是该结冰状态下直径分布函数和拟合函数式(1)对应的曲线图，其中k1= 0.0075，k2= 0.46，且求得孔隙率λ2D= 0.0512。

3.2 三维微观结构生成

指定结冰矩阵大小I × J × K 为270×270×270，建模中矩阵元素长度与真实结冰尺度之间的比例r = 27(像素/毫米)，即给定大小为270×270×270 的矩阵T = 0，其代表1 cm×1 cm×1 cm。

在结冰二维定量信息和拟生成结冰尺度基础之上，结合式(2)和式(3)可以确定孔隙的数量为N ≈1663。

在区间[0,2703]上按均匀方式生成N(=1663)个随机数Xi，i = 1,2,…,N，按照式(4)可以得到孔隙的位置信息。

图3 结冰显微图像及其分割结果Fig.3 Microscopic image of ice and its segmentation results

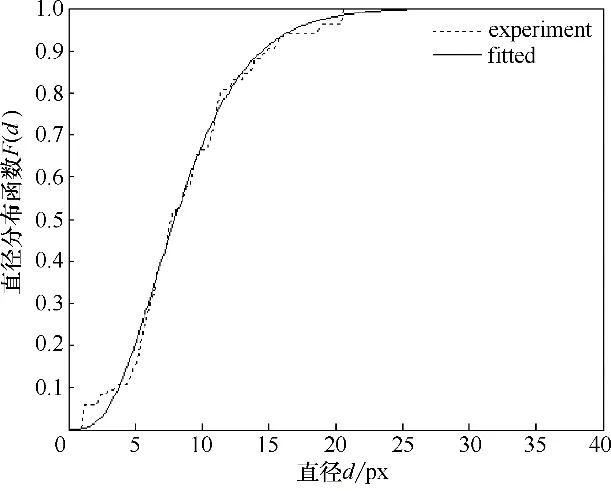
图4 结冰微观孔径分布曲线及其拟合曲线Fig.4 Distribution curves of micro pore diameter of ice and corresponding curve-fits

在区间[0,1]上按均匀方式生成N 个随机数Yi，i = 1,2,…,N，按 照 式(1)数 值 求 解 随 机 数Yi的 逆{F-1(Yi)|i = 1,2,…,N}，以此作为孔隙直径。

在得到孔隙球心位置及其直径的基础上，按照2.5 节扫描的方式对270×270×270 个矩阵元素进行赋值，得到最终的动态结冰三维微观结构模型，共耗时8.8 s。

图5 是在Matlab 中对该模型进行图像显示，黑色部分表示的是气泡孔隙；在Tecplot 中对其进行显示，并按照直径大小着色，结果展示于图6(a)，对模型0.25 等值面进行显示，结果展示于图6(b)。从图中可以看出，孔隙分布较随机，也较均匀，说明本文建模方法具有可行性。

3.3 方法的验证及可靠性分析

3.3.1 随机性验证 图7是确定孔隙位置和孔径分别所需的N(=1663)个随机数Xi和Yi,i = 1,2,…,N 随序号变化的示意图，其中横坐标是随机数序号i，纵坐标分别是随机数Xi和Yi的值。可以看出其满足第1 节中假设(3)和(4)的建模要求，并且具有较好的均匀性和随机性，这说明以本文方法模拟结冰内部孔隙的随机性是可行的。

图5 所生成1 cm×1 cm×1 cm结冰的图像显示Fig.5 Visional display of modeling ice with size of 1 cm×1 cm×1 cm

3.3.2 孔径分布吻合度 图8是生成的孔径分布与所服从的分布(1)之间的对比，它们之间的最大绝对误差为0.02，这说明吻合度较好，进而说明本文孔径生成方法是切实可行的。

3.3.3 二维信息定量对比 为了直观显示所生成的三维结构内部形态，图9 对比展示了结冰孔隙实验测量结果及所生成结冰二维截面。图中可以看出生成结冰的内部孔隙分布与实验较为相似，表现在孔隙大小、分布、随机性等方面。

实验图片的分割结果中，二维气泡的孔隙率约为0.0512，为了对比验证本文建模方法的准确度，对所生成结冰三维微观结构的所有x,y,z 方向的截面进行孔隙率计算，得到的结果以柱状图展示于图10中。可以看出它们的值主要集中在0.05 左右，变化范围有限，并且它们的平均值为0.0511，与二维实验值相近，这说明三维建模得到的孔隙率结果与二维定量结果有较高的一致性。

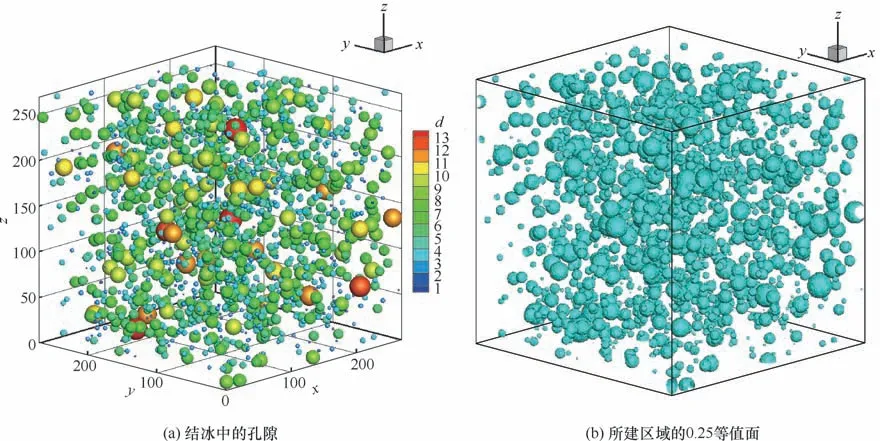
图6 所生成1 cm×1 cm×1 cm结冰的孔隙分布Fig.6 Pores distribution of modeling ice with size of 1 cm×1 cm×1 cm

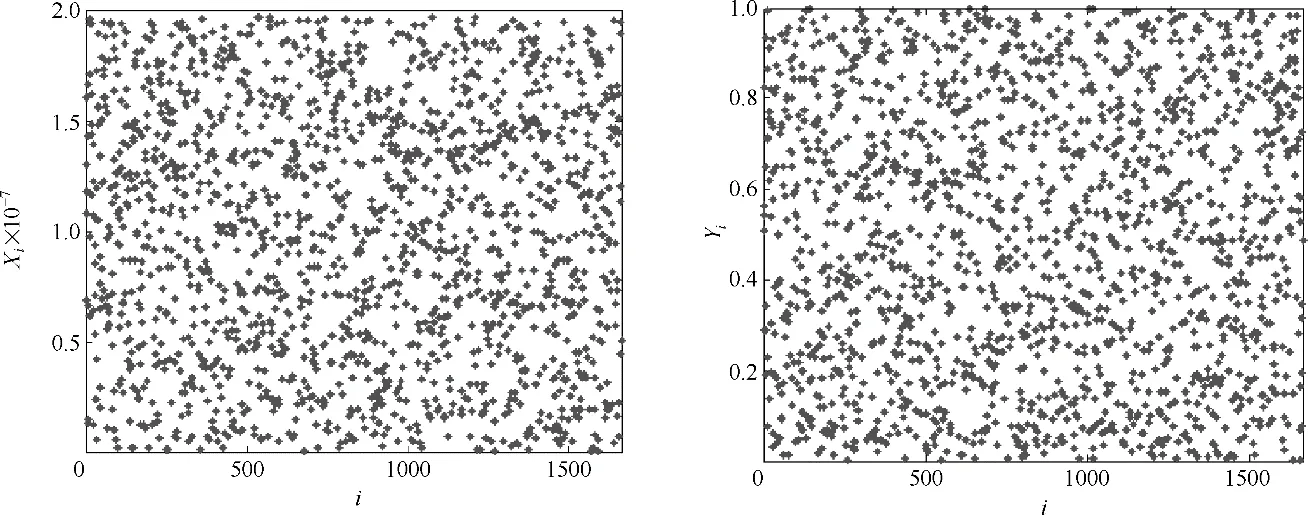
图7 孔隙位置与直径对应的随机数Fig.7 Random numbers for locations and diameters of pores

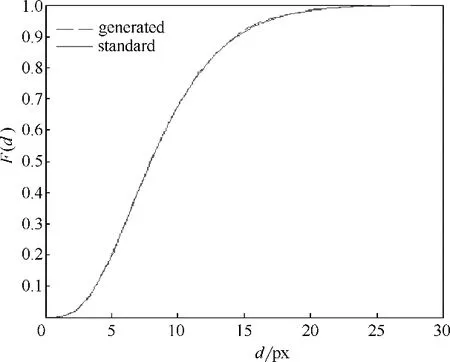
图8 生成孔径分布及其所服从的分布函数Fig.8 Distribution curves of modeling diameter and obeyed function

3.3.4 重复性实验 为了验证方法的可重复性，在保持所有输入条件相同的情况下，开展了100 次建模实验，并计算了它们的三维孔隙率，结果如图11所示。可以看出计算结果几乎全部在区间[0.047,0.054]上，并且它们的平均值为0.0506，与二维孔隙率0.0512 接近，这说明本文方法重复性较好，可靠性较高。

3.4 不同分辨率下的建模结果

考虑实际建模情况，需要生成不同分辨率下的结冰微观结构模型，即需要对比例因子r 进行适度调整。为了直观对比分辨率引起的不同，在本文比例尺r=27 的基础上[图12(b)]，分别增加了0.5 倍和2倍的缩放模型，结果分别展示于图12(a)、(c)中，对应真实结冰大小约为1.85 mm×1.85 mm×1.85 mm。从图中可以看出，随着分辨率的提高，即r 的增大，所建模中的球形表面“颗粒感”减弱，即气固界面更加光滑真实，并且更接近于真实球面。因此，如果需要更精细化的建模结果，提高比例尺r；反之则减小r。另外，相同参数设置下，CPU时间随着r的增大而增加。

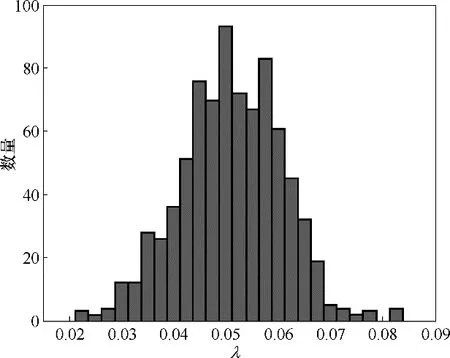
图10 x,y,z三个方向所有截面孔隙率Fig.10 Porosities of all cross-sections in x,y and z directions

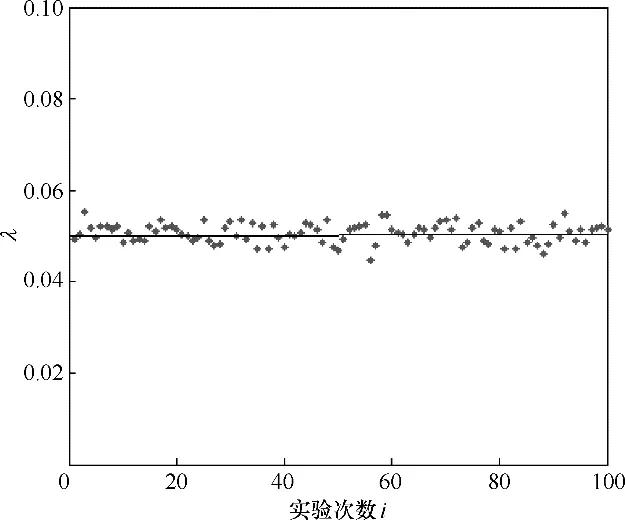
图11 重复实验得到的结冰三维孔隙率Fig.11 3-D porosities of ice by repetitive experiments

4 结 论

对动态结冰二维显微图像进行分割处理及定量分析，并基于此提出了结冰三维微观孔隙结构的建模方法，得到如下结论。

(1)建模方法是可行的。建模过程中包括孔隙类球形、孔隙随机性、孔径分布规律性等在内的定量依据均来自二维图像信息，建模方法的基础可靠；建模过程中，将二维定量信息推广至三维，遵循气泡孔隙的随机性、孔径分布等，实现方式有据、特征统一；实验部分对比验证了所生成结冰与实验所得结冰的二维微观定量信息，结果表明它们具有较高的相似度。

(2) 建模方法为结冰精细化研究提供新途径。在本文建模基础上，可以进行孔表面积、孔体积等三维孔隙空间结构特征参数的表征工作；可拓展至结冰生长模拟的微观展示方面，提高冰形计算精度；开展小尺度结冰融化过程模拟研究，改善现有结冰融化模型。

(3)建模方法尚有完善空间。为了数学化展示结冰三维微观形貌，建模方法必须基于一定假设，而文中假设来自于有限的研究工作，存在完善空间；二维定量信息取自远离基底表面的稳定生长段的实验结冰，实验结果不受基底表面物性参数影响，结果不能直接应用于基底表面结冰特征研究，且对结冰黏附力研究无指导意义。