基于正则化的函数连接神经网络研究及其复杂化工过程建模应用

贺彦林，田业，顾祥柏，徐圆，朱群雄

（1 北京化工大学信息科学与技术学院，北京100029； 2 智能过程系统工程教育部研究中心，北京100029；3中石化炼化（集团）股份有限公司，北京100101）

引 言

近年来，随着化工生产过程的日益复杂，生产过程数据也逐渐趋于高复杂、高非线性等特征，传统的基于化工机理建模的方法已经无法处理当下复杂的化工系统。神经网络技术作为一种新的数据驱动方法，其具有很强的非线性映射和学习能力，降低模型对机理的依赖，从数据的角度建立更加精确的模型，目前已经广泛应用于各个领域[1-3]，其衍生出了多种神经网络模型，如误差反向传播神经网络[4]（BP），多层感知器模型[5]（MLP）等。然而，BP 网络和MLP 网络的层数和节点数选取缺少理论依据，导致网络在计算复杂性和计算量上有一定难度，同时BP算法收敛速度缓慢。函数连接神经网络（functional link neural network，FLNN）[6-8]作为一种新型神经网络被Pao[9]提出，其网络结构简单，模型参数较少，具有非常好的非线性逼近能力。与传统神经网络结构作对比，函数连接神经网络只有输入层和输出层，没有隐藏层，因此函数连接神经网络计算量更小，训练速度更快，目前已经广泛应用于建模[10-11]、预测[12-13]、分类[14-15]等领域。

然而，随着工业系统规模的扩大，生产过程数据也越来越复杂，该网络存在一些局限性，经过函数连接神经网络扩展之后的数据维数和复杂度会更高，这大大提高了网络的计算量，从而降低网络的学习速度。同时由于FLNN 的权值求解方法采用的是梯度下降法，该方法的缺点是容易陷入局部极值，这会降低函数连接神经网络的网络精度。正则化是一种通过修正网络权值，从而有效解决高计算量以及局部极值问题的方法。该方法根据其自身的数学理论基础，充分利用输入与输出之间的关系，对输出代价函数进行约束，使代价函数的解最优化，同时由于约束参数的影响，使其一定程度上能够克服局部极值和过拟合问题[16-17]。函数连接神经网络通过使用正则化方法计算得来的权值来进行学习，在网络计算速度和精度上都有了提高。

由此，本文提出用正则化方法[18-21]来作为函数连接神经网络（FLNN）的权值更新方法，减少原始网络的计算量，提高模型精度和计算速度，改善了局部极值带来的影响，最终建立一种基于正则化的函数连接神经网络模型（regularization based functional link neural network,RFLNN）。为验证该网络模型的有效性，首先采用UCI 数据库中的Real estate valuation 数据对其进行验证；随后将所提出的模型应用于HDPE生产过程建模。

1 函数连接神经网络

函数连接神经网络采用函数扩展的方式，对原始输入进行扩展，使原始输入转化到另外一个空间，将增强后的模式作为网络输入层的输入，通过这种方法来更好地处理非线性问题。该神经网络由输入层和输出层构成，没有隐含层，因此相较于传统神经网络，该网络计算量更小，训练速度更快。

1.1 FLNN结构及构造方法

FLNN结构图如图1所示。

图1 常规FLNN结构Fig.1 Structure of the FLNN model

建立FLNN模型的具体步骤为：

（1）设n维输入向量：X =(x1,x2,…,xn)。

（2）对n维输入向量进行函数扩展[22-23]，扩展函数可选择如cos(πx)，sin(πx)，cos(2πx)，sin(2πx),…，设g(·)为扩展函数，经过扩展得到N维输入向量g(x) =(g1(x),g2(x),…,gN(x))。

（3）设W 为神经网络的权值向量：W =(w1,w2,…,wn)T，将扩展后的输入向量与权值向量加权求和，得输出层的输入向量，即S =∑gw。S经过激活函数f(·)处理，则得到该神经网络的输出Y。

（4）将计算得出的网络实际输出Y 与期望输出d 对比，求得误差函数e(t)。通过误差函数e(t)的变化来对权值向量W 进行调整，直到满足神经网络精度要求，或者学习次数终止为止。多次调整得来的权值即为FLNN的网络模型参数。

1.2 传统FLNN的局限性

常规FLNN 权值更新的方法一般是BP 算法[24-25]，将神经网络的实际输出量与期望输出量差值的平方和最小化作为神经网络的学习目标，数学公式为[26]

权值更新公式为

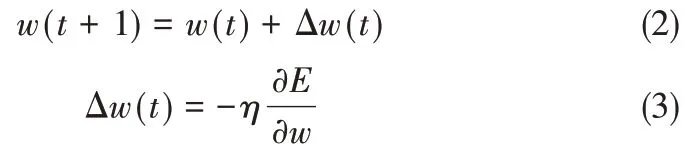
其中，η为学习率;t为固定时延。

将FLNN 网络应用到化工过程建模中，不可避免会遇到一些问题。

（1）FLNN 自身权值更新采用的是BP 算法，而BP 算法通过使用梯度下降法来求解误差函数E 的最小值，而这种方法的缺点[27-29]是容易陷入局部极值，同时BP 算法也容易出现过拟合的问题，因而会导致模型精度降低、收敛速度慢等问题。

（2）由于FLNN 采用的是先将原始数据进行增强扩展，而化工数据的高维度和高复杂化，会导致扩展之后的数据更加复杂，因而大大提高网络计算量，降低网络的计算速度和精度。

为了克服这些问题，本文结合正则化的方法，对FLNN 网络的权值参数进行优化，通过使用正则化方法求得的权值，作为网络的训练最终结果，从而提高网络的性能。

2 基于正则化方法的FLNN神经网络

由于目前化工过程的日益复杂，过程数据也趋于高维化和复杂化，这导致常规的FLNN 在处理这些数据时，出现训练速度偏慢、网络精度低的问题。本文采用正则化的方法，对FLNN 进行权值参数的优化改进，不仅在计算速度上有了提升，而且网络精度也有一定的提高。

2.1 正则化方法

正则化方法[30]其目的是通过将神经网络代价函数最小问题的求解限制在一个压缩子集中，利用正则化项平衡模型的网络偏差，控制输出的权值范围，从而提高网络的稳定性。其经验公式为L=E+λF。其中，L 为正则化代价函数，E 为神经网络损失函数，λ为正则化参数，F为正则化项。

下面对经验公式各项进行具体的说明。

（1）损失函数 该函数用E 表示，设xi为训练样本；训练输出，即逼近函数为f(xi)；标准损失函数表达如下

其中，di为训练的期望输出。

（2）正则化项 用F 表示，根据逼近函数，将正则化项定义为

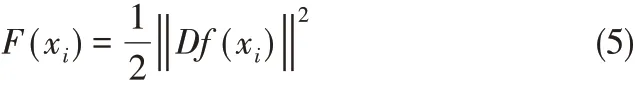
其中，D是线性微分算子，包含损失函数解的问题的先验知识，因此D的选取与所解的问题有关，它使正则化问题的解稳定，使解满足连续性要求。

（3）正则化代价函数 令正则化代价函数为L，结合式（4）中损失函数和式（5）中正则化项，L 最终表达为

其中,λ 是正则化参数，通常为正实数，用来控制正则化项F 和代价函数L 的最终解。当λ→0 时，则代价函数L 最小点问题的求解是无约束的，完全由样本确定最终解；当λ→∞时，则表明样本是不可靠的，代价函数L最小点问题的求解是不存在的；因此，通过训练样本和先验知识，选择一个合适的λ值，对求解L(xi)起很大的作用。本文选取的正则化参数λ=0.1。

正则化问题的解就是使代价函数L 最小化，根据微分的规则，对代价函数L(xi)进行Frechet 微分，有

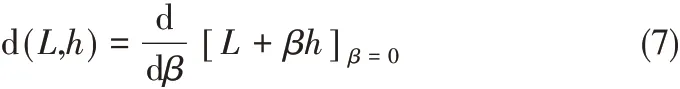
其中，h(x)是一个固定的关于向量x 的函数；为了简化表示，用h来代替h(x)。

根据微分规则，对于h ∈x 集合，代价函数L(xi)有极值点的必要条件是

其中，d(E,h)与d(F,h)分别是损失函数E(x)和正则化项函数F(x)的Frechet微分。

代价函数L(x)的Frechet微分结果如下

根据Green恒等式，可以将式（9）改写为

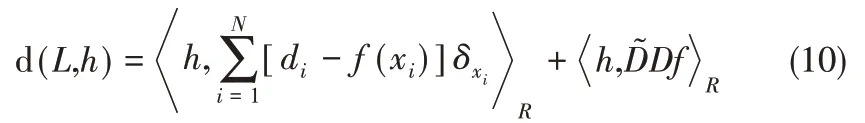
最终计算得

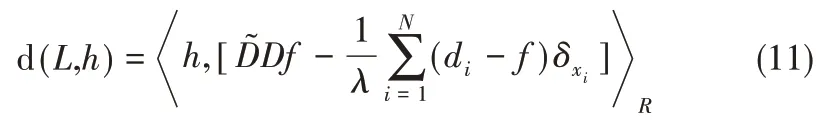
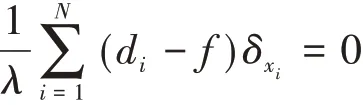
由Green函数的连续性可知

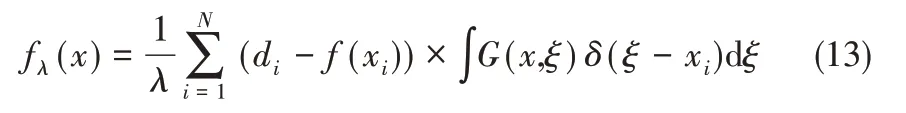
其中，fλ(x)为代价函数L(x)的最小解在经过N个Green 函数的线性叠加；G(x,ξ)是关于x 的Green函数，ξ为定值。

对式（13）化简可得

令权值

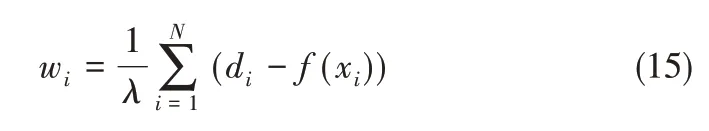
则

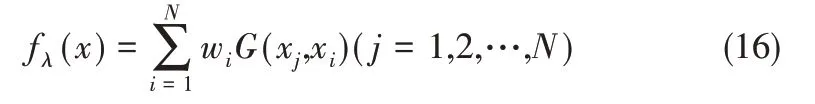
将式（15）、式（16）写成矩阵形式

其中，fλ、d、G、W 分别为fλ(x)、di、G(xj,xi)、wi的矩阵表达。

式(17)、式(18)相消可得

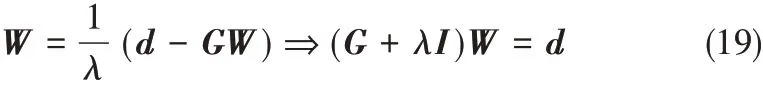
其中，I为N × N的单位矩阵。

当矩阵(G + λI)是正定矩阵时，权值W 可表示为

由于式(20)求解权值的解局限于权值W、Green函数G、期望输出d 是相同维数的，因此为了得到通用解W，引入N × N的对称阵G0，使得

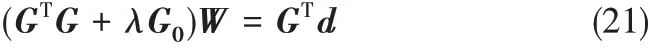
得权值的最终解为

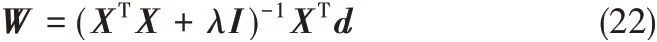
2.2 基于正则化的FLNN

本文提出基于正则化的函数连接神经网络，网络结构图如图2所示。

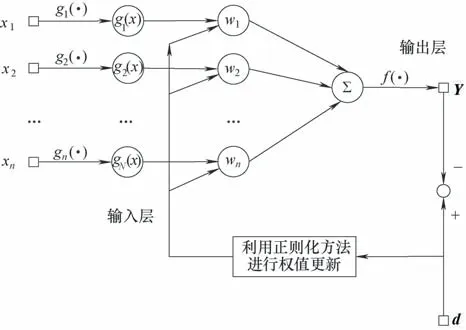
图2 RFLNN网络结构Fig.2 Structure of R-FLNN model

给定网络训练样本集合S，S 中包含K 组高维数据S ={(Xk,Yk)|k = 1,2,…,K; Xk∈RL; Yk∈RJ}，其中每个训练样本的输入含有L个属性，输出含有J个属性。对于训练样本S，建立RFLNN模型如下。

（1）数据预处理：由于数据中各个变量的量纲不一定相同，使得数据与数据之间没有可比性，因此需要对给定的输入样本数据进行归一化处理，本文设定的归一化范围为（0.1,0.9），归一化函数为

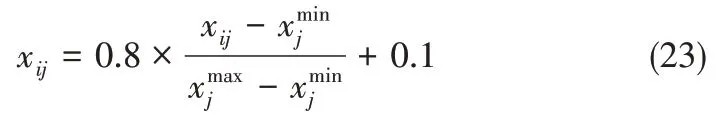
（2）函数扩展：选择扩展函数对归一化后的数据进行函数扩展，增强数据的非线性，本文选用的扩展函数有正弦函数g1(·)、余弦函数g2(·)、Sigmoid函数g3(·)。通过扩展，提高输入数据的维度，扩展后的数据变为N维网络输入变量

数据集变化为S'={(Xn,Yk)|Xn∈RI; Yk∈RJ;n = 1,2,…,N; k =1,2,…,K}，其中RI是经过函数扩展之后的新输入样本集合，RJ保持不变。

（3）建立RFLNN 模型，以扩展后的数据Xn作为输入层的输入，通过正则化方法求解出输入层与输出层之间的连接权值

其中，Yk为FLNN 网络的期望输出，Yk∈RJ，n =1,2,…,N; k = 1,2,…,K。

（4）训练：对RFLNN模型进行训练，将训练得出的最终数据yi进行反归一化，并计算实际输出与期望输出的相对误差。反归一化公式为

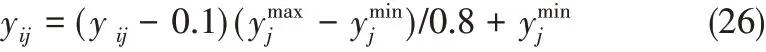
（5）泛化：利用泛化样本的数据对训练好的RFLNN 网络进行验证，计算网络泛化的期望输出和实际输出之间的相对误差。算法流程图如图3所示。

3 实验结果分析

利用UCI 数据库中的Real estate valuation 数据集以及化工行业HDPE 的生产数据对所提出的RFLNN模型进行验证，并与传统FLNN对比。

3.1 标准数据实验分析

为初步验证此方法的可行性和有效性，本文采用UCI 数据库中的Real estate valuation 数据集对所提出的RFLNN 模型进行测试，Real estate valuation数据是一个对房地产估价的数据集，有6 个输入属性和1 个输出属性，共414 组数据，随机分为训练数据（总数据的三分之二）和泛化数据（总数据的三分之一）。

图3 RFLNN网络算法流程Fig.3 Flowchart of R-FLNN algorithm

设置网络的输入层和输出层节点数为6和1，传统FLNN 网络的学习因子设为0.1，迭代次数为1000次。将数据分别作为RFLNN 和传统FLNN 的输入，得到网络训练的残差分布，如图4所示。

图4 网络训练过程的残差分布Fig.4 Residual error distribution of real estate valuation data training examples with two models

从图4 可以看出，网络训练得出的输出与真实值相近，可以说明网络有效性和可行性。

对网络的实际输出与真实值进行对比，计算出训练阶段和泛化阶段的平均相对误差，比对结果如表1所示。由表1 的对比结果可以看出，RFLNN 相对传统FLNN 训练和泛化平均相对误差都有降低，说明RFLNN 网络泛化能力更强，精度更高，在局部极值和过拟合问题方面处理地较好。

表1 UCI数据集模型建模时间和精度对比Table 1 Performance comparisons of models for estate valuation data

3.2 HDPE工业应用数据实验分析

3.2.1 HDPE 简介 高密度聚乙烯（high density polyethylene，HDPE），是一种结晶度高、非极性的热塑性树脂，主要用于生产薄膜、管材等塑料产品。生产高密度聚乙烯采用的是德国Basell 的Hostalen低压淤浆工艺进行悬浮聚合，该装置主要以乙烯为原料，1-丁烯为共聚单体，用氢气调节分子量，通过将乙烯、1-丁烯、氢气、催化剂等连续加入聚合反应器内，控制好聚合物的质量，从而生产高密度的聚乙烯。因此，为了生产高密度的聚乙烯，控制好聚合物的质量，对国内外相关企业在减小损失和生产成本方面起积极作用。

依据工业机理和经验知识，确定输入变量为15、输出变量为1的样本数据集，其中样本数据集的输入变量是主要影响聚合物质量的15个因素，输出变量为密度指数。通过对现场采集数据，并对数据进行融合、滤波、去干扰等预处理后，共采取135 组生产数据，随机选取90组数据（总数据的三分之二）作为训练数据，其余45组数据（总数据的三分之一）作为泛化数据，传统FLNN 学习因子为0.1，迭代次数为1000次，传统FLNN 和RFLNN 输入层和输出层节点数分别为15和1。

3.2.2 训练结果对比 图5为网络训练的输出和真实值对比图，图6是网络训练的残差分布。

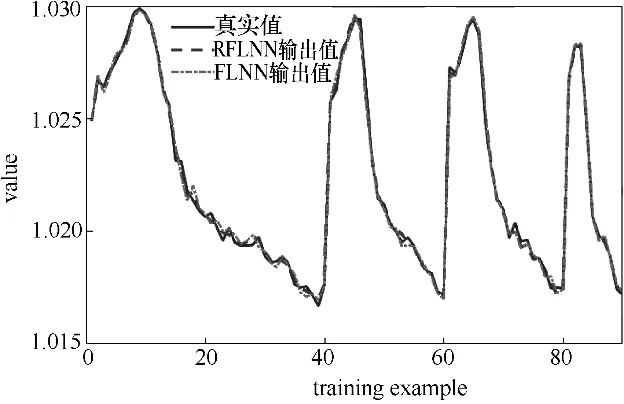
图5 网络训练的输出和真实值的对比Fig.5 Comparisons of training examples with two models

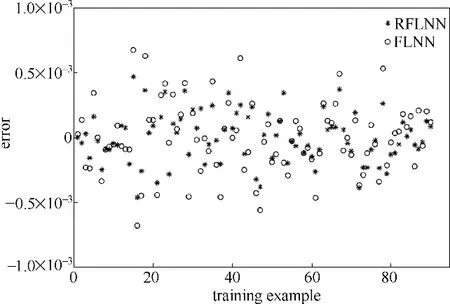
图6 网络训练的残差分布Fig.6 Residual error distribution of training examples with two models

从网络训练输出与真实值的对比图及残差分布图可以看出，RFLNN 网络训练输出更加接近真实值，RFLNN网络训练的平均相对误差是0.0156%，而传统FLNN网络训练的平均相对误差是0.0214%，相对误差较小，说明训练过程中RFLNN网络模型更精确。从训练时间角度可以看出，RFLNN 网络训练时间为0.0024 s，传统FLNN 网络训练时间为0.3918 s，训练时间明显缩短，说明RFLNN 网络计算量降低，收敛速度更快。

3.2.3 泛化结果对比 图7为网络泛化的输出和真实值对比图，图8为网络泛化的残差分布图。

RFLNN 网络的泛化平均相对误差是0.0365%，而FLNN网络泛化的平均相对误差是0.0505%，由此说明RFLNN网络泛化精度更高。

FLNN 和RFLNN 网络应用于HDPE 过程建模在训练和泛化所花时间，以及平均相对误差比对结果如表2所示。

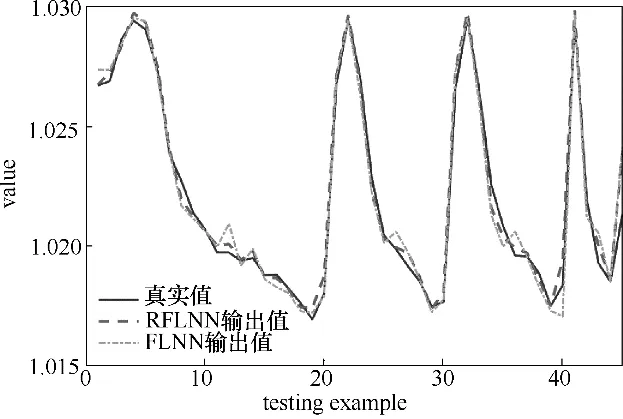
图7 网络泛化的输出与真实值的对比图Fig.7 Comparisons of testing examples with two models

图8 网络泛化的残差分布Fig.8 Residual error distribution of testing examples with two models

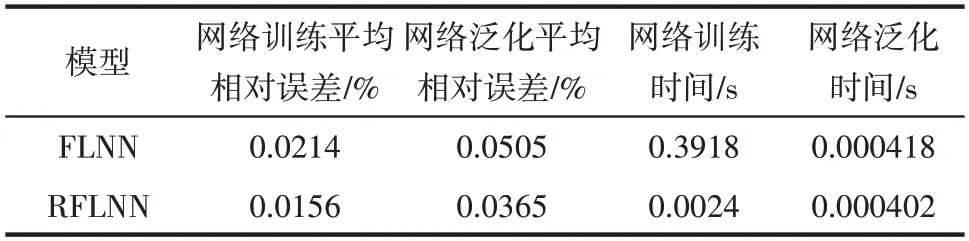
表2 工业建模应用时间和精度对比Table 2 Comparisons of model performance for HDPE samples

通过表2 可以看出，RFLNN 网络训练和泛化的平均相对误差都有所降低，说明了本文提出的RFLNN 网络模型精度更高，泛化能力更强，且在保证模型精度的情况下，RFLNN网络收敛速度更快。

4 结 论

针对复杂的化工过程建模问题，本文提出了一种基于正则化的函数连接神经网络模型，此模型是在传统的FLNN 网络模型的基础上，通过对权值更新的算法进行优化，利用正则化方法计算权值的优越性，从而改善网络处理数据的性能，提高网络的学习速度和精度。为了验证所提模型的有效性，本文选取UCI 标准数据Real estate valuation 以及HDPE 生产过程数据进行仿真实验。仿真结果表明，本文所提出的基于正则化的FLNN 模型相比于传统的FLNN 模型，具有收敛速度快、模型精度高、泛化能力强的优点，且能够有效避免局部极值和过拟合的问题，为复杂石化过程建模提供新思路。