如何在小学课堂教学中渗透数学思想

陆保恩

【摘要】数学思想是数学素养的核心内容，培养学生的数学思想、数学思维是小学数学课堂教学的重要内容。因此，小学数学教师要利用课堂教学的有利时机，从低年级开始对学生进行数学思想渗透，引导学生运用数学思想解决问题，促进学生数学思维能力的发展，从而实现提高学生解决问题能力的目的。

【关键词】小学数学课堂;数学思想;数学思维;解题能力

数学是研究数量关系、空间结构变化等知识的一门学科。数学知识体系包括数学知识、数学方法、数学思想三个层次。其中，数学思想是数学知识的本质，是对数学规律的总结与升华。掌握了数学思想，就相当于掌握了数学的精髓。因此，小学数学教师在教学过程中不仅要给学生传授数学知识，而且要利用一切时机对学生进行数学思想的渗透，让学生从低年级开始就学会运用数学思想去解读数学概念、数学规律，解决数学问题，从而实现提高数学课堂教学效率、提高学生数学核心素养的目的。

一、在数学知识讲解时渗透数学思想，帮助学生理顺思维方向

课堂教学是教师传授新数学知识的主要手段，教师在新知识的具体讲解过程中要注意数学思想的渗透，运用转化思想将新数学知识转化为学生熟悉的数学问题，让学生在学习数学知识的同时能够接受数学思想的熏陶，从而达到理顺学生的思维方向、形成丰富的学习正能量的目的。

【教学案例1】教师在小学低年级的数学教学当中常常感到“学生好像什么都会了，没什么可教的”。的确，学生好像已经能轻松完成50以内甚至100以内的加减法，或者已经能熟练背诵出乘法口诀，可是学生的数学思想、数学思维体系还没有建立、发展起来，他们对数学知识的掌握还停留在表面，没有形成严谨、科学的认识或理论。这就需要教师适时地渗透数学转化思想，把学生从生活中掌握的、只停留于表象的认识转化到理性的数学思考、数学思维上，让学生真正做到数学表达和数学思考。

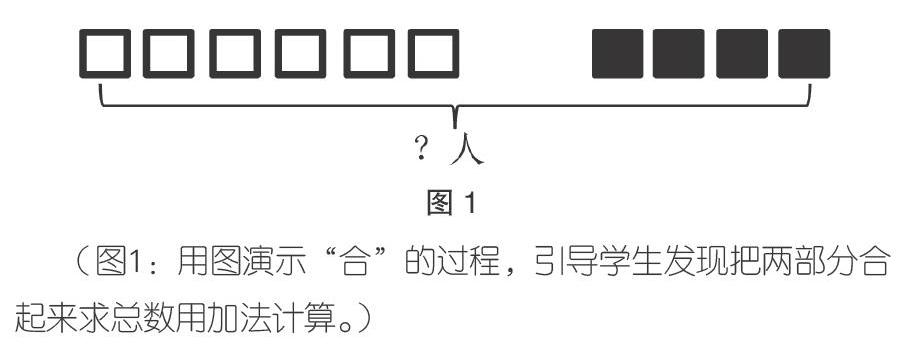
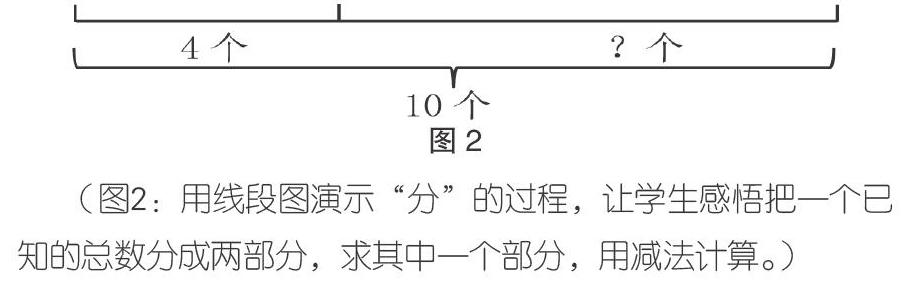
例如，在教学“10以内的加减法”时，学生会遇到这样一些问题。①教室里有6个女学生，4个男学生，教室里一共有几个学生？②小嘉有10个苹果，送给小明4个，自己还剩几个苹果？凭借已有的生活经验和直觉，学生立刻能说出：“教室里有6个女学生，4个男学生，一共有10个学生，用加法计算‘6+4=10;小嘉有10个苹果，送给别人4个，那自己就少4个苹果，应该用减法计算‘10-4=6，自己还剩6个苹果。”但是学生这样的表达是不够的，是浅显的。教师可以通过画图的方式（如图1、图2），引导学生运用观察、比较、分析、转化等方法，运用数学思维、数学语言概括出符合数学逻辑的表达：“把两部分合起来求总数用加法计算;把一个已知的总数分成两部分，求其中一个部分，用减法计算。”

在新知识的传授过程中，教师要有意识地对学生进行数学思想渗透，让学生从低年级开始就知道把生活问题数学化，把生活直觉转化为数学思考，从表面的现象中探索到数学深层次的奥秘，实现了学生从形象思维到抽象思维的跨越，从而帮助学生理顺思维的方向，提高学生分析问题和解决问题的能力。

二、在题目审查时渗透数学思想，整合学生的思维角度

在解答数学问题时，如果题目逻辑关系、数量关系梳理不清，就容易把学生引入错误的思维角度，无法正确解答问题。因此，审题是解决数学问题的基础和关键。教师要引导学生运用数学思想对题目展开仔细审查，整合学生的思维角度，找出正确的逻辑关系和各种等量关系，理顺其内在关联。在审题过程中，教师要给学生渗透数学思想方法，让学生借助数学思想方法展开相关操作，找出题目中隐藏的条件和数量关系，给学生提供更多的学习启示。数学思想不仅是学习理念，更是科学的学习方法，教师要让学生合理运用数学思想展开问题解读，最后找出正确的解题方法。

【教学案例2】小学三年级开始，学生会遇到比较复杂的数学问题。这些复杂的数学问题往往只给出间接的解题条件，或者把重要的解题条件、数学关系隐藏起来。这就要求学生在审题时运用数学思想，厘清题目的逻辑关系、数量关系，找出隐藏的条件和关联条件，正确解决数学问题。

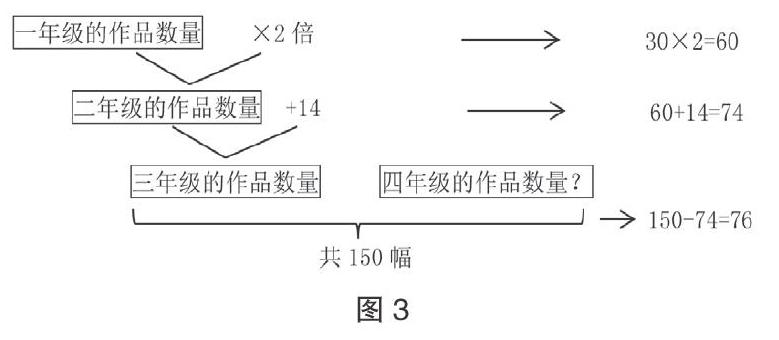
例如习题：“学校举行画展，一年级展出绘画作品30幅，二年级展出的作品是一年级的2倍，三年级展出的作品比二年級多14幅，四年级和三年级一共展出150幅，请问四年级展出作品多少幅？”

这道习题中的数量关系比较复杂，教师要给学生渗透数学思想，指出正确的思维方向，厘清题目的数量关系，解决问题，如图3。

教师可以引导学生分析、审查题目，整合学生的思维角度，找出隐藏的数量关系，提高学生解决问题的效率。

三、在教学活动设置时渗透数学思想，扩展学生思维宽度

《义务教育数学课程标准（2011年版）》明确指出：“教师应激发学生的学习积极性，向学生提供充分从事数学活动的机会，帮助他们在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想和方法，获得广泛的数学活动经验。”[1]饶有趣味的数学教学活动不仅增强了课堂的趣味性，而且让学生在互动活动中建立了学科认知基础。因此，教师在设计教学活动时，要根据教学内容适时渗透数学思想方法，扩展学生思维宽度，提升课堂教学的有效性。

【教学案例3】小学二年级下册，学生就开始接触图形，从点到线再到面，从四边形、三角形、圆形到多边形，从平面图形到立体图形，学生对图形的学习是不断深入的。对于图形与几何的教学，教师进行数学教学活动的设计时就要考虑对学生进行数形结合思想的渗透，让学生在“数”与“形”的转化与联系中找出蕴藏的数量关系，得到更多的学习启迪。数形结合是一种重要的数学思想，它可以把抽象的数量关系与形象直观的图形巧妙地结合来，不仅可以增强学生学习数学的兴趣，加深学生对数学概念的理解，而且可以发展学生的逻辑思维能力和空间观念，提高学生的智力发展水平，扩展学生思维宽度。

例如，在教学四年级下册“三角形三边关系”时，教师可以设计有趣的教学活动，让学生进行实验操作，动手摆出图形，运用数形结合的思想总结出数学规律。在课前，教师为学生准备好不同长度的小棒，让学生动手试试能不能围成三角形。①小棒的长度分别为2cm、3cm、6cm;②小棒的长度分别为3cm、6cm、9cm;③小棒的长度分别为6cm、7cm、8cm;④小棒的长度分别为5cm、9cm、9cm。

学生们纷纷动手进行实验……

生1：第一组2cm、3cm、6cm的三根小棒不能围成三角形。两根小棒的长度加起来没有另一根小棒长，所以两边的和小于第三边，不能围成三角形（如图4）。

生2：第二组3cm、6cm、9cm三根小棒也不能围成三角形。两根小棒的长度加起来刚好等于另一根小棒长度，怎么摆也围不成三角形（如图5）。

生3补充：第二组3cm、6cm、9cm三根小棒，两边的和刚好等于第三边，这两边和第三边重合了，也不能围成三角形。

生4：第三组6cm、7cm、8cm三根小棒可以围成三角形（如图6）。

生5：第四组5cm、9cm、9cm三根小棒可以围成三角形（如图7）。

在学生动手实验之后，教师与学生一起总结：什么情况下才能围成三角形呢？最终得出结论：任意两边的和都必须大于第三边。

数形结合思想的渗透，让学生从直观的图形中总结出抽象的数学规律。这样的教学活动不仅为学生提供了交流合作的时间，而且为学生提供了自主探索的空间。学生在动手实验的过程中发现问题，解决问题，相互启发，共同提高，获得了成就感，实现了数学思维的内化和提炼。

数学思想是数学的灵魂、精髓和核心，是学生分析问题、解决问题的有效手段和制胜法宝，也是学生把知识内能转化为能力外能的桥梁。因此，在小学课堂教学过程中，教师要根据课堂实际情况和学情，运用多种教学手段，加强数学思想的渗透，提高学生灵活运用数学思想的能力，实现学生数学核心素养的提高。

【参考文献】

中华人民共和国教育部.义务教育数学课程标准（2011年版）[M] .北京：北京师范大学出版社，2012.