浅谈数形结合在小学数学教学中的应用

梁艳华

【摘要】数形结合不仅是一种重要的数学思想方法，而且是有效地决问题的方法。在小学数学教学过程中，教师要适当地引入数形结合方法，帮助学生理解数学概念，分析数学问题，解决数学问题。相遇问题是人教版小学数学五年级上册的重要内容，教师可以在教学中引入数形结合方法，帮助学生快速地分析题目，建立等量关系，提高解决问题的效率。

【关键词】相遇问题;数形结合;小学数学教学

我国著名数学家华罗庚先生说过：“数形结合百般好，割裂分家万事非。”[1]“数”与“形”是事物中两个不可分割的属性，数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，帮助学生把复杂的问题简单化、抽象的问题具体化。数形结合不仅是一种重要的数学思想方法，而且是有效地解决问题的方法。在小学数学教学过程中，教师要给学生适当地引入数形结合方法，帮助学生理解数学概念，分析数学问题，解决数学问题。

相遇问题（两个物体从两地出发相向而行，经过一段时间必然在途中相遇，这类问题被称为相遇问题）是人教版小学数学五年级上册的重要内容，也是学生觉得比较难解决的问题。解决相遇问题的关键是厘清时间、速度和路程三者之间的数量关系。教师在教学相遇问题时，可以引进数形结合方法，让学生借助直观图形，分析时间、速度和路程三者之间的数量关系，建立等量关系，提高问题的效率。

一、以形析题

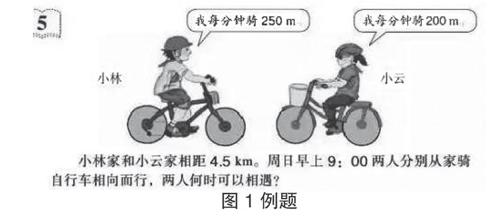
人教版小学数学五年级上册第五单元“实际问题与方程”中出现了用方程求解相遇时间的问题（题目如图1），要求学生在全面理解、分析题目之后列出方程，求相遇的时间。题目的条件比较复杂，教师可以引入数形结合的方法，引导学生通过以形析题，把题目中的条件用线段图详细画出来，让学生直观地对题目数量关系进行分析和判断，把抽象、复杂的数量关系变得具体和形象。

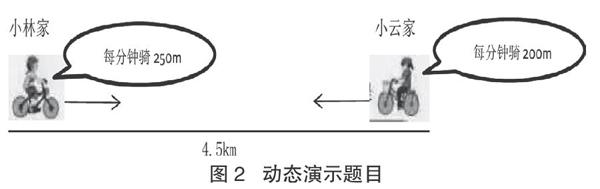
师：请同学们仔细观察一下，小林、小云这两位同学同时出发，他们是怎么走的？（教师出示动态课件，如图2。）

师：在数学上把这样面对面地行走称为相向而行。相向而行必然会相遇，那么经过多久两人会相遇呢？

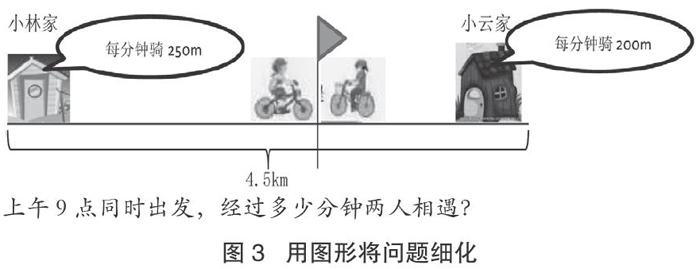
（教师用数形结合的方式，用小问题将大问题细化，帮助学生精准地把握题目的有效解题信息。）

上午9点同时出发，经过多少分钟两人相遇？

学生观察图后，用自己的话完整地说出题目的意思，把握题目的有效解题信息。

生：小林和小云两家相距4.5km，一天早上9点，两人分别从家出发，骑自行车相向而行，小林每分钟骑250m，小云每分钟骑200m，经过多少分钟两人相遇？

师再抛出一个问题让学生思考：假如小林从出发到遇到小云花了5分钟，那么小云从出发到与小林相遇用了几分钟？他们两人从出发到相遇所用的时间怎么算呢？

生：应该也是5分钟吧。

师：对的。他们两人从出发到相遇，所用的时间应该相同，这个时间被称为相遇时间。这节课我们就一起来研究与相遇时间有关的相遇问题。

数形结合，运用图形来分析问题，不仅可以帮助学生更好地厘清题目的数量关系，而且可以让学生理解新的知识点。因此，数学教师在教学过程中要注意培养学生运用数形结合的方法分析题目，引导学生画出简单的线段图分析题目，提高学生的数学思维能力。

二、以形解题

运用数形结合的方法分析问题之后，教师还可以引导学生运用数形结合的方法解决问题，帮助学生将抽象的数量关系形象化、具体化，降低问题的难度，让学生比较容易找出题目中的等量关系。

教师用线段图，提炼题目的数量信息，让学生通过观察找出题目的等量关系（如图4）。

小林每分钟骑250米                                  小云每分钟骑200米

师：观察线段图，同学们发现什么呢？旗子左边是小林骑的路程，旗子右边是小云骑的路程，他们两人路程合在一起会怎样？同学们发现什么等量关系？

生：小林骑的路程+小云骑的路程=总路程。

师：你们能观察线段图，根据这个等量关系列出方程吗？

生：假设两人x分钟后相遇，根据等量关系，小林骑的路程+小云骑的路程=总路程，250x+200x=4500，x=10。两人骑行10分钟可以相遇。

师：250x和200x各表示什么意思？

生：250x表示小林骑的路程，200x表示小云骑的路程，两人各自骑的路程合起来就是总路程。

教师继续引导学生。

师：同学们还能找到其他的等量关系吗？如何检验x=10是不是正确？还有什么方法解决这个题目的问题？

（教师用动态图形帮助学生发现其他等量关系，找出其他解题方法。）

师：如图5所示，两人同时出发骑了1分钟，①表示小林1分钟骑的路程，②表示小云1分钟骑的路程，将这两条线段合在一起代表什么呢？

生：线段①和线段②合在一起代表两人1分钟骑的路程，也就是两人每分钟骑的路程之和。

师：两人继续骑行，又骑了2分钟，一共骑了3分钟，那他们3分钟骑行的路程之和怎么计算？

生：两人每分钟骑的路程之和×3。

师：如果两人一直骑到相遇，那么他们相遇的时间也就是他们骑行的时间。你们可以找到什么样的等量关系？

生：两人每分钟骑的路程之和×相遇时间=总路程。

师：请同学们根据这个等量关系列出方程式。

生：（250+200）x=4500，x=10。

师：同学们，现在我们运用了两种不同的方法、两种不同的方程来解决这道题目，谁能说出这两个方程有什么不同？

生：根据不同的等量关系列出不同的方程。

这道相遇问题的题目，用方程来求解相遇时间有两种基本的等量关系：①小林骑的路程+小云骑的路程=总路程;②两人每分钟骑的路程之和×相遇时间=总路程。教师要充分利用图形直观、生动的特点，运用数形结合的方法，帮助学生从复杂的数量关系中提炼、凸显最本质的等量关系，让学生找到解决问题的突破口，快速解决问题。

三、以形助思

数形结合是一种重要的数学思想方法，它不仅可以帮助学生快速、有效地解题，而且可以培养学生的数学思维。小学生的形象思维比较强，抽象思维能力比较薄弱，教师要通过一些练习使数形结合方法在学生的思维中得到强化，提高学生对数学本质的理解，促進学生的形象思维能力与抽象思维能力的协调发展。

师：这三道练习题有什么相同点吗？请说说自己的想法。

生：都是求“相遇时间”。

师：对的，都是求“相遇时间”，都可以用图形表示出来。

通过引导学生画图，这些求“相遇问题”的行程问题、工作问题、工程问题都可以用简单的线段图形表示出来，让“数”转化为“形”，再由“形”转化为“数”，在“数”与“形”的转化过程中，将抽象问题转变为图形问题，帮助学生直观地对数量关系进行分析和把握。

总之，教师要在数学教学的每个细节当中，最大限度地渗透数形结合思想，帮助学生把握数学本质，培养学生的逻辑思维能力，提高学生分析问题、解决问题的能力。

【参考文献】

胡杨.渗透数形结合思想，提高高中数学教学效果[J].中学课程辅导，2015，9（21）：284.